Abstract
Quantum-photonic chips, which integrate quantum light sources alongside active and passive optical elements, as well as single-photon detectors, show great potential for photonic quantum information processing and quantum technology. Mature semiconductor nanofabrication processes allow for scaling such photonic integrated circuits to on-chip networks of increasing complexity. Second-order nonlinear materials are the method of choice for generating photonic quantum states in the overwhelming majority of linear optic experiments using bulk components, but integration with waveguide circuitry on a nanophotonic chip proved to be challenging. Here, we demonstrate such an on-chip parametric down-conversion source of photon pairs based on second-order nonlinearity in an aluminum-nitride microring resonator. We show the potential of our source for quantum information processing by measuring the high visibility anti-bunching of heralded single photons with nearly ideal state purity. Our down-conversion source yields measured coincidence rates of 80 Hz, which implies MHz generation rates of correlated photon pairs. Low noise performance is demonstrated by measuring high coincidence-to-accidental ratios. The generated photon pairs are spectrally far separated from the pump field, providing great potential for realizing sufficient on-chip filtering and monolithic integration of quantum light sources, waveguide circuits and single-photon detectors.
Similar content being viewed by others
Introduction
Photons are excellent quantum information carriers because they combine high speed with long coherence times at room temperature1, 2. Photon-pair sources based on spontaneous parametric down-conversion (SPDC) have enabled major advances in photonic quantum computation and communication3, 4. Quantum teleportation5, 6, 7, multi-photon manipulation8, 9, 10, 11, 12, 13, 14, quantum algorithms15, 16, 17, 18, 19 and loophole-free tests of local realism20, 21 were all achieved with down-conversion photons generated in materials with strong second-order (χ(2)) optical nonlinearities. Common nonlinear crystals, for example, lithium niobate (LiNbO3), are centimeter-sized and not yet compatible with standard nanofabrication technologies22, 23, 24. Silicon-based nanophotonic chips have emerged, which leverage mature semiconductor-fabrication processes to provide a stable and scalable solution for optical quantum information processing2, 25, 26, 27, 28. However, the generation of down-conversion photons for current experiments with silicon photonic chips still relies on separate bulk optic setups. One alternative approach resorts to exploiting the χ(3) optical nonlinearity of silicon, which allows for generating correlated photon pairs via the process of spontaneous four-wave mixing (SFWM)29, 30, 31. However, integrating an optically pumped source of correlated photons with waveguides and detectors on the same chip requires one to efficiently separate the generated signal and idler photons from the co-propagating classical pump field. In the SFWM process, the generated photon pairs are spectrally separated by only a few nanometers from the optical pump wavelength, which hence makes sufficient filtering and integration of such sources with detectors on one chip a challenging task. Because on-chip pump-light suppression requires sophisticated techniques32, a variety of critical physical processes could only be realized using SFWM in combination with off-chip filtering, for example, in source multiplexing33, on-chip quantum interference31 and entanglement34, 35, 36. SPDC offers better prospects for efficient pump-light suppression and, consequently, for integrating the source and detector on the same chip. For example, efficient filtering37 can be achieved for a down-conversion photon-pair source on a silicon substrate, where the pump light is in the visible wavelength range and the photon pairs are generated at infrared (IR) wavelengths. The material absorption of silicon for visible light is then large enough (1740 dB cm−1) to guarantee efficient suppression of undesired pump light before photon pairs reach an on-chip detector.
Aluminum nitride (AlN) is a new material suitable for scalable photonic integrated circuits38, 39. Its strong intrinsic second-order nonlinearity (χ(2)) not only shows great potential for realizing on-chip photon-pair sources based on SPDC39 but also permits integrated low-loss, high-speed electro-optic phase modulation38. Here, we demonstrate an integrated down-conversion photon-pair source using a high quality-factor (Q) AlN-microring resonator. For compatibility with telecommunication technology, we realize nonlinear conversion of visible-wavelength (775 nm) pump photons to telecom-wavelength (1550 nm) photon pairs. The high refractive index contrast between the AlN waveguides and a silicon-dioxide (SiO2) cladding layer allows for small device footprint and enables dense integration on silicon handles. The generated photon pairs are characterized by waveguide-coupled superconducting single-photon detectors (SSPDs) integrated on a dedicated chip. Apart from high source brightness, we also observe high-visibility anti-bunching of heralded single photons. The suitability of our source for quantum information applications is further highlighted by the nearly ideal purity of the heralded photons, which we demonstrate in self-correlation measurements of the idler photons.
Materials and methods
Experimental setup and device engineering
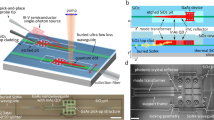
The device is shown in Figure 1a. We realize the down-conversion source as a high quality-factor AlN-microring resonator, which enhances the pump-photon interaction with the material’s χ(2) nonlinearity40. This allows for the production of down-conversion photon pairs with long coherence times at low optical-pump power. Here, the visible-wavelength pump laser field is guided into the microring resonator via a narrow wrap-around waveguide, while the generated IR-photon pairs are coupled out via a wider bus waveguide. We design an on-chip wavelength-division multiplexer (WDM), which guides IR photons back into the optical fiber towards the detectors. After passing through a fiber-coupled silicon filter, the residual visible pump photons are rejected while IR photons are guided to waveguide-coupled SSPDs, which are integrated on a separate chip27, 28, 41 inside a cryostat. Waveguide directional couplers on this detection chip allow for 50/50 splitting of photon pairs before detection with the SSPDs and signal analysis with time-correlated single-photon counting (TCSPC) electronics.
On-chip SPDC photon-pair source. (a) Schematic illustration of an on-chip photon-pair source based on a χ(2) nonlinearity connected to SSPD on another chip. Higher-energy pump photons (visible wavelengths) are coupled to a microring resonator and the generated lower-energy photon pairs (IR wavelengths) are randomly split on the detector chip for coincidence measurements with integrated SSPDs. A fiber-coupled silicon filter (labeled as off-chip filter) is used to reject the remaining pump light reflected back from the fiber-to-chip interface. (b) Effective refractive indices of modes in microring. The phase-match condition is satisfied with waveguide width around 1.10 μm. Lower-left inset: the cross-section of the AlN waveguide. Insets on the right: The electric field profiles at the cross-section of microring of two phase-matched modes. (c–e) Device images of AlN down-conversion photon-pair source. The white dashed box shows the enlarged region. (c) Optical image of an array of microring photon-pair sources with on-chip WDMs. (d) Enlarged image of a single microring resonator with both IR (top) and visible (bottom) bus waveguides. (e) SEM picture showing the coupling region of visible light bus waveguide (narrow) with microring resonator (wide).
The lower left inset in Figure 1b shows a cross-section of the AlN chip. AlN forms the core of the waveguide while SiO2 acts as a low refractive index cladding layer, on top of the silicon substrate. A degenerate (non-degenerate) SPDC process involves one optical-pump mode in the visible-wavelength band and one (two) signal and idler mode(s) in the IR-wavelength band. Energy conservation implies the condition ωvis = ωIR,1 + ωIR,2, while momentum conservation requires mvis = mIR,1 + mIR,2, where ωx and mx (x = vis, IR, 1 or IR, 2) are the frequencies and azimuthal numbers of the visible and IR modes, respectively (for degenerate down-conversion, ωIR,1 = ωIR,2 and mIR,1 = mIR,2). To fulfill these two conditions and realize efficient nonlinear conversion, it is necessary to match the effective refractive indices neff = mxc/ωxr (where c is the speed of light in vacuum and r is the radius of the microring) of the visible pump and IR signal and idler modes. This phase-matching condition can be satisfied for a higher-order transverse-magnetic (TM) visible-wavelength pump mode and fundamental TM (TM0) signal and idler modes in the IR39, 42. In Figure 1b, we show how this effective refractive-index matching is achieved for a 775-nm TM2 mode and a 1550-nm TM0 mode by engineering the waveguide width of the AlN microring. In the right two insets of Figure 1b, the corresponding mode profiles in a 1.10 μm width waveguide are shown.
The high refractive-index contrast between waveguide (AlN) and cladding (SiO2) materials allows for a small device footprint and dense integration. In Figure 1c, we show an optical micrograph of an array of AlN-microring photon-pair sources integrated with on-chip WDMs. Two independent waveguide channels are designed for visible and IR light, respectively (Figure 1d). To excite the visible-wavelength TM2 mode inside the ring resonator, we utilize a narrow wrap-around waveguide. Adjusting the gap between the ring and the wrap-around waveguide as well as the wrap-around waveguide width, it is possible to adiabatically couple the TM0 pump mode of the feed waveguide to the TM2 mode of the microring under critical coupling conditions. As long as the gap between the wrap-around waveguide and the microring is large enough, the existence of this narrow waveguide will not cause deterioration of the quality factor for the ring resonator’s IR modes (see Supplementary Section I). The wrap-around waveguide is tapered down to 100 nm, as shown in the SEM image of the coupling region (Figure 1e), while the coupling gap between the wrap-around waveguide and microring is 500 nm.
Device fabrication and measurement
A 1-μm thin AlN film is sputtered on a commercial oxide-on-silicon wafer. We use FOX-16 resist and define patterns in electron-beam lithography. After development in an MF312 developer, Cl2/BCl3/Ar chemistry is used to etch into the AlN layer. The chip is then coated with a 2.5-μm PECVD-oxide cladding layer for protection during subsequent polishing steps. The device is finally annealed in an O2 atmosphere for 5 h at 950 °C to improve the quality of the PECVD oxide. The detector chip is fabricated from a commercial 330-nm SiN-on-insulator wafer, onto which we sputter an 8-nm thin film of NbTiN. Electrode pads are defined in PMMA resist via electron-beam lithography followed by gold deposition and lift-off in acetone. In a second electron-beam lithography step, the SSPD nanowires are patterned in HSQ negative-tone resist and transferred into the NbTiN layer using CF4 chemistry. In the third and final electron-beam lithography step, the SiN waveguides are written in ZEP positive-tone resist followed by a timed reactive-ion etch in CHF3/O2 chemistry.
We use a continuous-wave visible-wavelength laser (TLB-6712) to pump the SPDC source. A fiber-coupled silicon absorber (OZ optics) is used to filter out the pump light reflected from the fiber-to-chip interface. We achieve 80-dB attenuation for pump light at 3-dB insertion loss for IR light. For the degenerate SPDC coincidence measurement, a band-pass tunable filter is used to spectrally select the degenerate down-conversion photons. For the measurements of the SPDC thermal state, a dense wavelength-division multiplexer (DWDM) is used to select the idler branch from the nearest non-degenerate down-conversion photon pair. The photons are then sent to the detector chip, where SSPDs are integrated with a 50/50 directional coupler for self-correlation measurements28. Electrical signals from the on-chip detectors are sent into a TCSPC system (Picoharp 300, Rudower Chaussee 29, 12489 Berlin, Germany) for time tagging43. For non-degenerate cross-correlation measurements, a DWDM is used to separate signal and idler photons, which are then sent to two separate on-chip detectors for coincidence measurement.
Results and discussion
Characterization of on-chip down-conversion source
We first characterize the classical performances of the microring resonator. Figure 2a shows the microring transmission spectrum for visible light in a slightly under-coupled configuration (a critically coupled spectrum is shown in Supplementary Section I). The visible resonance near 775 nm, which is used in the following experiment, has a quality factor of 1.1 × 105. Figure 2b shows the transmission spectrum of IR light when the bus waveguide is critically coupled to the microring resonator. The IR resonances show a typical quality factor of 2 × 105. The two spectra illustrate how the TM2,2N mode at 775 nm aligns with the TM0,N mode at twice the wavelength according to energy conservation (ωvis = 2ωIR). Here, N (2N) stands for the azimuthal mode number, which is determined by momentum conservation (mvis = 2mIR) in the degenerate SPDC process. To perfectly fulfill the energy conservation (ωvis = 2ωIR), we vary the global temperature of the chip and determine the optimized working temperature using second-harmonic generation (SHG)38, 39 as a figure of merit, which is directly related to SPDC efficiency (see the theoretical derivation in Supplementary Section III). By pumping in TM0,N mode and monitoring the output SHG from TM2,2N mode, we observe a maximum SHG efficiency of  , where PSHG (Pp) is the optical power of the generated second-harmonic light (pump laser). Due to the group-velocity mismatch between the visible and IR modes, energy conservation cannot be satisfied for SHG in other modes, as can be seen in Figure 2a and 2b, where no pairs of IR- and visible-light modes are aligned, except for the TM2,2N and TM0,N modes. However, the group-velocity dispersion is relatively small in the IR region, and energy conservation can be fulfilled for IR modes over a wide wavelength range for difference/sum frequency generation (DFG/SFG) and, conversely, for non-degenerate SPDC. We verify this by fixing the visible-wavelength pump laser at the resonance of the TM2,2N mode and sweeping the IR probe laser over a wavelength range covering the neighboring resonances (for example, TM0,N−1/TM0,N−2/TM0,N−3 modes). We observe DFG of various modes, as shown in Figure 2c. The fact that both SHG and various DFG configurations can be observed indicates the possibility of generating both degenerate and non-degenerate photon pairs in wavelength bands spaced similarly to a frequency comb.
, where PSHG (Pp) is the optical power of the generated second-harmonic light (pump laser). Due to the group-velocity mismatch between the visible and IR modes, energy conservation cannot be satisfied for SHG in other modes, as can be seen in Figure 2a and 2b, where no pairs of IR- and visible-light modes are aligned, except for the TM2,2N and TM0,N modes. However, the group-velocity dispersion is relatively small in the IR region, and energy conservation can be fulfilled for IR modes over a wide wavelength range for difference/sum frequency generation (DFG/SFG) and, conversely, for non-degenerate SPDC. We verify this by fixing the visible-wavelength pump laser at the resonance of the TM2,2N mode and sweeping the IR probe laser over a wavelength range covering the neighboring resonances (for example, TM0,N−1/TM0,N−2/TM0,N−3 modes). We observe DFG of various modes, as shown in Figure 2c. The fact that both SHG and various DFG configurations can be observed indicates the possibility of generating both degenerate and non-degenerate photon pairs in wavelength bands spaced similarly to a frequency comb.
Linear and nonlinear characteristics of the χ(2) source. (a,b) Transmission spectra of the microring resonator. Four gray dashed lines are aligned with the visible TM2 mode resonances. Gray region shows the phase-matched mode pair (TM2,2N and TM0,N) for SHG and degenerate SPDC, whose resonances are aligned within the linewidth of IR-mode resonance. (a) Visible light transmission spectrum, with TM2 mode resonances emphasized by red lines. The quality factor of the visible optical mode (TM2,2N) is 1.1 × 105. (b) IR-light transmission spectrum, with TM0 modes identified by the azimuthal mode number. The typical quality factor of the IR mode is 2 × 105. (c) Difference frequency generation (DFG) measured by optical spectrum analyzer. Peaks due to input IR pump lasers are shown in the light orange region and generated DFG signals are shown in the light green region. Visible pump laser with 1.9 mW power on chip is fixed on resonance with TM2,2N mode. (d) Single-photon flux arriving at the detector chip from the degenerate and nearest three groups of non-degenerate down-conversion. The counts are calibrated by the wavelength-dependent detection efficiency (Supplementary Section II).
We use SSPDs to characterize the statistical properties of photons generated by the SPDC source. In Figure 2d, the photon flux for different ring resonances is shown for fixed power and wavelength of the visible-light pump laser. The variation in the detected photon rates for different resonance wavelengths can be explained by the difference in the quality factors of the IR resonator modes because the photon-pair generation rate is linearly dependent on the quality factor. As discussed in the Supplementary Information, the bandwidth for non-degenerate SPDC can be as large as 40 nm.
Correlated photon-pair generation
The statistical properties of the generated photon pairs can be analyzed in terms of the second-order correlation function (g(2)), which we measure using two detectors at the outputs of a beam splitter and normalize to photon flux44

where Rcc is the coincidence count rate, R1 (R2) is the count rate of detector 1 (2), and τb is the coincidence time window. Here, the coincidence rate Rcc is a function of the photon-photon arrival-time delay τ, while R1, R2 and τb are constant, which are combined to obtain the accidental coincidence rate Rac = R1 R2 τb. We note that the g(2) (τ) function is a rescaling of coincidence rate Rcc (τ) by accidental coincidence rate Rac. While the values of Rcc and Rac are both dependent on the losses of the measuring systems, the value of g(2) (τ) is independent of system losses, allowing us to directly extract the pair-generation rate and SPDC photon bandwidth from the measured g(2) (τ) function.
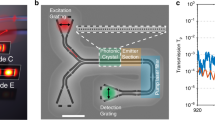
For degenerate SPDC photon pairs, we measure the self-correlation function with two waveguide-coupled SSPDs integrated with a 50/50 directional coupler, as sketched in the left inset of Figure 3a. We observe a clear coincidence peak centered at zero delay time, which indicates strong temporal correlations between the photons emitted from the SPDC source. The second-order self-correlation function for degenerate SPDC photon pairs is given by45, 46, 47
Second-order correlation function (g(2)(τ)) of down-conversion photons. (a) Self-correlation measurement of degenerate down-conversion photon pairs. Right inset: Power dependence of degenerate photon-pair generation rate. Normalized generation rate of 3.0 MHz mW−1 has been fitted. (b) Cross-correlation measurement of the nearest non-degenerate down-conversion photon pairs. (c) Self-correlation measurement of the idler in the nearest non-degenerate down conversion. The left insets in a–c show the schematics of each measurement. The solid lines are fittings with the convolution function between a double exponential decay and a Gaussian distribution function related to the chosen bin width and detector jitter.

where τ is the delay time between two photons, τc is the coherence time of the SPDC photons and R is the photon-pair generation rate. Here, random fluctuations in the arrival time (δτ) of photons have to be taken into account because the detector jitter (τj=18 ps; see Supplementary Section V) and the coincidence time window (τb = 70 ps) are not negligible compared with the photons’ coherence time (τc. Assuming the arrival-time fluctuations δτ follow a normal distribution  , with standard deviation
, with standard deviation  , the correlation function can be expressed as (see Supplementary Section V)
, the correlation function can be expressed as (see Supplementary Section V)

where  and erf(x) is the error function. From a fit to the data in Figure 3a, we obtain the degenerate photon-pair generation rate R=5.9 MHz for a 1.9 mW pump power on chip. The bandwidth of the photons extracted from the fit to the data is
and erf(x) is the error function. From a fit to the data in Figure 3a, we obtain the degenerate photon-pair generation rate R=5.9 MHz for a 1.9 mW pump power on chip. The bandwidth of the photons extracted from the fit to the data is  , which agrees with the measured linewidth of the IR resonator mode. This indicates that the coherence time of the generated photon pairs is determined by the lifetime of the signal/idler mode. The photon-pair generation rate as a function of pump power is shown in the right inset of Figure 3a. We obtain a generation rate of 3.0 MHz mW−1 for degenerate SPDC.
, which agrees with the measured linewidth of the IR resonator mode. This indicates that the coherence time of the generated photon pairs is determined by the lifetime of the signal/idler mode. The photon-pair generation rate as a function of pump power is shown in the right inset of Figure 3a. We obtain a generation rate of 3.0 MHz mW−1 for degenerate SPDC.
For non-degenerate SPDC photon pairs, the photons of a pair may have different wavelengths. If we discard all the signal photons and only measure the emission of idler photons, thermal-state statistics is expected48. We measure the self-correlation function for the nearest idler (TM0,N−1) photons, as shown in the inset of Figure 3c. We obtain g2(0) = 2.07 ± 0.12 from a fit to the data in Figure 3c, which is in agreement with the expected value of g2(0) = 2 for a single-mode thermal state44, 49.
We then separate signal and idler photons using a DWDM and use two independent waveguide-coupled SSPDs to measure the second-order cross-correlation function between signal and idler, as shown in the inset of Figure 3b. For non-degenerate photon pairs, the cross-correlation function is given as

From a fit to the data in Figure 3b, we extract the photon-pair generation rate of R=11.0 MHz for 1.9 mW pump power (5.8 MHz mW−1), and the bandwidth  , which is similar to the degenerate SPDC case. We conclude that non-degenerate SPDC is approximately two times more efficient than degenerate SPDC, which matches well our theoretical calculation and originates from the different coefficients of the interaction Hamiltonian for degenerate and non-degenerate SPDC processes (Supplementary Section III). Additional cross-correlation measurements for photon pairs emitted into other microring resonance modes are shown in the Supplementary Information. The total (including degenerate and different groups of non-degenerate) photon-pair generation rate for this AlN microring source is more than 20 MHz mW−1, which is comparable or even higher than the state-of-the-art SPDC photon-pair source using bulk or waveguide-based χ(2) crystals24. Regarding the spectral brightness, the AlN microring source is much brighter due to the microring's narrow linewidth.
, which is similar to the degenerate SPDC case. We conclude that non-degenerate SPDC is approximately two times more efficient than degenerate SPDC, which matches well our theoretical calculation and originates from the different coefficients of the interaction Hamiltonian for degenerate and non-degenerate SPDC processes (Supplementary Section III). Additional cross-correlation measurements for photon pairs emitted into other microring resonance modes are shown in the Supplementary Information. The total (including degenerate and different groups of non-degenerate) photon-pair generation rate for this AlN microring source is more than 20 MHz mW−1, which is comparable or even higher than the state-of-the-art SPDC photon-pair source using bulk or waveguide-based χ(2) crystals24. Regarding the spectral brightness, the AlN microring source is much brighter due to the microring's narrow linewidth.
Source of heralded single photons
Single-photon sources45, 46, 50 are a critical component for quantum information processing. Quantum-dot systems51, 52 have recently been explored for the on-demand generation of single photons with non-classical correlations. However, SPDC sources, such as the one used in this work, produce photon pairs probabilistically. Nevertheless, single-photon generation can be realized with an SPDC source by applying a heralding technique, i.e. one of the generated photons of a pair is detected, thus heralding the presence of its partner photon in a single-photon state. In our experiment, with 1.9-mW on-chip pump power, the photon-pair generation rate for the nearest non-degenerate modes (TM0,N+1 and TM0,N−1) is 11.0 MHz. As stated above, the signal or the idler beam itself is in a thermal state, showing bunching statistics with g(2)(0)=2. However, one can use the signal photon to herald the appearance of the idler photon, in which case the heralded idler photon shows non-classical anti-bunching behavior. To verify that our photon-pair source can be used as a heralded single-photon source, we measure the normalized idler-idler self-correlation function conditioned on the detection of a signal photon45, 53:

where Piis is the coincidence rate of detecting one idler and two signal photons, g(2)si is the second-order cross-correlation function and r (τ) is the first-order correlation function53. Here, three detectors are needed. One detector is used to measure the signal photon as the heralding trigger, while the other two detectors measure the self-correlation of the heralded idler photons. We are interested in the special case in which g(2)h (τ) ≡ g(2)h(0,τ|0). For an ideal photon-pair source, we expect to detect at most one idler photon upon detection of one (heralding) signal photon. Thus, an anti-bunching dip around zero delay time (τ=0) is expected. In our experiment, we split up the nearest non-degenerate photon pairs deterministically using a DWDM. We then use the signal photon as a herald for the detection of its partner photon and measure the autocorrelation function for the latter. The inset of Figure 4 shows a schematic diagram of the experimental setup. Figure 4 shows the measurement result with no background noises or dark counts subtracted. A clear anti-bunching dip near zero delay time is observed. We extract g(2)h(0)=0.088±0.004<<0.5 from the data, which confirms that our SPDC source indeed yields heralded single photons.
Heralded signal-signal correlation function (g2h(τ)) of down-conversion photons. An on-chip pump power of 1.9 mW is used to obtain a sufficiently high counting rate. Here, the heralded anti-bunching dip of g2h(0)= 0.088±0.004 indicates that the photon-pair source is operating in the single-photon regime. Inset shows the schematics of the measurement setup.
Device losses and measuring efficiencies
The raw data of the coincidence measurements are shown in the Supplementary Information. The measured coincidence rate is approximately 80 Hz. For a pump power of 1.9 mW on chip, we infer an emission rate of photon pairs in the nearest non-degenerate modes of 11.0 MHz from a fit to the coincidence data in Figure 3b. The difference between these rates arises from losses at the various device interfaces, that is, microring-to-waveguide interface (3 dB) and fiber-to-chip interface (3.5 dB), at the silicon filter (3 dB), at the DWDM (6 dB) and due to non-ideal detector efficiency (10 dB). Without subtracting any background noise or dark counts, we find a coincidence-to-accidental ratio of 560 for a minimum pump power of 0.6 mW, at which the on-chip generation rate amounts to 3.5 MHz. We expect that, in future experiments, high-efficiency waveguide-coupled SSPDs27, 28, 41, 54 or semiconductor avalanche single-photon detectors55 will be integrated alongside the source on the same chip. This will greatly increase the measured coincidence rate because the optical loss at photonic interfaces is minimal in such implementations.
On-chip WDM
The significant difference between the pump and signal/idler wavelengths in the SPDC process allows for a variety of design choices to separate pump light from the generated photons. One could choose to exploit wavelength-selective material absorption, for example, silicon will strongly absorb visible light but transmit IR light. Another approach is to design WDM waveguide circuits. In this work, we choose to realize the latter option because a WDM structure has the additional benefit of simplifying the fiber-to-chip coupling interface: (i) When characterizing the IR and visible performances of the microring, only one optical fiber at each side of the photonic chip is needed. (ii) When characterizing the down-conversion photon pairs, a single optical fiber is simultaneously used to send the pump light into and collect generated photon pairs from the chip (as shown in Figure 1a). The designed WDM structure employs tapered waveguide couplers, as shown in Figure 5a and 5b. In dielectric waveguides, the optical mode confinement decreases as wavelength increases, such that IR light will have a longer-range evanescent field outside the waveguides compared to visible light. For two waveguides in close proximity, the resulting coupling is stronger for IR than for visible light. We hence adjust the coupling length such that IR light is efficiently transferred from one waveguide to another (Figure 5a) while visible light remains unaffected and is transmitted through the coupling region without coupling to the neighboring waveguide (Figure 5b).
On-chip WDM. (a,b) Simulated electric-field profiles of the designed on-chip WDM device for IR (λ=1550 nm) and visible (λ=775 nm) light. (c) Coupling efficiency of IR light to cross port and visible light to drop port. Inset, Zoomed-in image of coupling efficiency for coupling lengths ranging from 200 to 400 μm.
Here the adiabatic-taper WDM design is realized with high fabrication tolerances and broadband working wavelength. The relationship between coupling efficiency and coupling length is shown in Figure 5c for λ=1550 nm and 775 nm. The design shown in Figure 5a and 5b corresponds to a coupling length of 350 μm and a gap of 0.4 μm. With increasing coupling length, the cross-port coupling for IR light increases monotonically and saturates at 100%, while the visible-light transmission into the drop port decreases linearly with coupling length but remains above 99% over the entire range. The inset of Figure 5c shows that coupling efficiencies into the cross and drop ports of more than 99% are achieved simultaneously for IR and visible light, respectively, for coupling lengths ranging from 250 to 400 μm. This performance corresponds to 20-dB suppression of visible pump light with less than 0.044-dB insertion loss for IR light for each of the on-chip WDM structures. In future implementations, a cascade of such WDMs could be used for realizing sufficient suppression of guided pump light. Note that, in the current experimental configuration, a portion of the pump light is directly reflected back into the optical fiber from the fiber-to-chip interface and is thus guided towards the detectors. To suppress these residual pump photons, we use an additional off-chip fiber-coupled silicon filter.
Discussion
The high-visibility anti-bunching of heralded single photons shown in Figure 4 confirms the non-classical character of our SPDC source. However, for quantum information processing, it is desirable to generate photons in a pure state56. We use the Schmidt number, K, to describe any remaining entanglement between optical modes of an SPDC pair. The Schmidt number K, heralded single-photon state purity P and second-order self-correlations are related via g(2)(0)=1+1/K=1+P49, 56. Ideal heralded purity (P=1) is obtained if all measured photons are found in the same optical mode (K=1). Conversely, if photons are found in multiple output modes (K>>1), the correlation function g(2)(0) approaches 1 and the heralded purity approaches 0. In our experimental configuration, down-conversion photons will only be emitted into TM0 modes because other spatial modes do not fulfill the phase-matching condition. These TM0 modes are spectrally separated by at least one free spectral range, as shown in Figure 2d. Selecting one of these modes with a bandpass filter thus yields single-mode emission. The measured g2(0)=2.07±0.12 (P=1.07±0.12) in Figure 3c confirms that our SPDC source indeed achieves single-mode emission and nearly ideal (unit) heralded purity.
In addition to the purity of generated photons, sufficient on-chip pump rejection is a key requirement for achieving source-detector integration on the same chip. Here, we discuss the prospects of realizing sufficient on-chip filtering. (i) Suppressing guided pump light in photonic waveguide circuits: The filtering of pump photons propagating inside a waveguide could, for example, be achieved by depositing a thin layer of silicon on top of the waveguide-interfacing source (circuit) and detector. Silicon has an absorption coefficient of 1740 dB cm−1 for the pump wavelength (775 nm) at cryogenic temperatures, while being transparent for down-conversion photons (approximately 1550 nm). The hybrid AlN-silicon waveguide hence results in significant selective absorption of pump photons. Alternatively, five cascaded on-chip WDMs (as described above) could also provide efficient pump-light rejection. (ii) Suppressing unguided pump photons propagating in free space and in substrate and cladding materials: Photons incident from free space can efficiently be absorbed in a metal layer covering the area where the detectors are located51. Pump photons scattered into a transparent substrate, however, pose a significant challenge in SFWM experiments, where the pump light in the telecom band near 1550 nm can propagate losslessly in the cladding (usually SiO2) and substrate (usually silicon) materials and finally couple to the detection region, which limits the on-chip filter’s performance32. In our case, however, the visible pump photons scattered into the silicon substrate layer are efficiently absorbed due to the large material absorption. Pump photons coupled directly from the input fiber into SiO2 slab modes may propagate for somewhat longer distances before leaking into the underlying silicon substrate of higher refractive index. Numerical simulations show that the attenuation of slab modes is>90 (200) dB cm−1 for a 3 (2) μm thick SiO2 buffer layer. Hence, detectors can be efficiently shielded from pump photons propagating inside the cladding layer if they are separated by a centimeter from the fiber-to-chip interface.
Entanglement4, 35, 36 is an important resource for quantum information processing and quantum communications57, 58. Entangled photon pairs produced via SPDC in nonlinear bulk crystal4 and SFWM in microrings35, 36 show great promise for quantum-technology applications. Based on our work, we anticipate that entangled photon-pair generation in on-chip SPDC sources will be demonstrated in future work, benefitting scalable quantum information processing on silicon chips.
AlN has a χ(2) coefficient (4.7 pm V−1)39 that is almost ten times smaller than that of LiNbO3 (41.7 pm V−1)59. However, using advanced nanofabrication techniques, we are able to realize microring resonators with high quality factors, which results in a resonant-pump power enhancement that compensates for the weaker nonlinear coefficient. This is confirmed by comparing the SHG efficiency achieved in our AlN device (1.16 W−1) to recently reported SHG efficiencies in LiNbO3 microdisks (0.109 W−1)59, 60. We see the potential for further enhancement of the nonlinear conversion efficiency for AlN microring resonators by decreasing the ring radius and improving the quality factor of the microring resonator. We believe that a fivefold increase in quality factors and a threefold decrease in radius are achievable in future AlN devices, which would bring SHG efficiencies of 400 W−1 within reach.
Conclusion
In conclusion, the demonstrated photon-pair source based on the χ(2) nonlinearity of AlN microring resonators and the quantum-correlation measurement with waveguide-integrated single-photon detectors constitute an exciting step towards fully integrated photonic quantum circuits. Compared to photonic circuits fabricated from more traditional semiconductor materials, for example, silicon-on-insulator, AlN permits high-quality (high-brightness, high-purity, low-noise) correlated photon-pair emission that is spectrally far separated from the pump light. AlN-on-insulator therefore holds great potential for realizing efficient pump suppression and monolithic integration of non-classical light sources with single-photon detectors on the same chip. Additionally, high-speed phase modulation via the electro-optic effect will enable real-time circuit reconfiguration. In combination with high-efficiency single-photon detectors, it will thus be possible to generate non-classical photonic states and implement feed-forward schemes as well as quantum logic operations in a scalable manner.
References
Kok P, Munro WJ, Nemoto K, Ralph TC, Dowling JP et al. Linear optical quantum computing with photonic qubits. Rev Mod Phys 2007; 79: 135–174.
O’Brien JL, Furusawa A, Vučković J . Photonic quantum technologies. Nat Photonics 2009; 3: 687–695.
Burnham DC, Weinberg DL . Observation of simultaneity in parametric production of optical photon pairs. Phys Rev Lett 1970; 25: 84–87.
Kwiat PG, Mattle K, Weinfurter H, Zeilinger A, Sergienko AV et al. New high-intensity source of polarization-entangled photon pairs. Phys Rev Lett 1995; 75: 4337–4341.
Bouwmeester D, Pan JW, Mattle K, Eibl M, Weinfurter H et al. Experimental quantum teleportation. Nature 1997; 390: 575–579.
Ma XS, Herbst T, Scheidl T, Wang DQ, Kropatschek S et al. Quantum teleportation over 143 kilometres using active feed-forward. Nature 2012; 489: 269–273.
Bussières F, Clausen C, Tiranov A, Korzh B, Verma VB et al. Quantum teleportation from a telecom-wavelength photon to a solid-state quantum memory. Nat Photonics 2014; 8: 775–778.
Peruzzo A, Lobino M, Matthews JCF, Matsuda N, Politi A et al. Quantum walks of correlated photons. Science 2010; 329: 1500–1503.
Matthews JCF, Politi A, Stefanov A, O’Brien JL . Manipulation of multiphoton entanglement in waveguide quantum circuits. Nat Photonics 2009; 3: 346–350.
Shadbolt PJ, Verde MR, Peruzzo A, Politi A, Laing A et al. Generating, manipulating and measuring entanglement and mixture with a reconfigurable photonic circuit. Nat Photonics 2012; 6: 45–49.
Huang YF, Liu BH, Peng L, Li YH, Li L et al. Experimental generation of an eight-photon Greenberger–Horne–Zeilinger state. Nat Commun 2011; 2: 546.
Pan JW, Chen ZB, Lu CY, Weinfurter H, Zeilinger A et al. Multiphoton entanglement and interferometry. Rev Mod Phys 2012; 84: 777–838.
Spring JB, Metcalf BJ, Humphreys PC, Kolthammer WS, Jin XM et al. Boson sampling on a photonic chip. Science 2013; 339: 798–801.
Broome MA, Fedrizzi A, Rahimi-Keshari S, Dove J, Aaronson S et al. Photonic boson sampling in a tunable circuit. Science 2013; 339: 794–798.
Lu CY, Browne DE, Yang T, Pan JW . Demonstration of a compiled version of Shor’S quantum factoring algorithm using photonic qubits. Phys Rev Lett 2007; 99: 250504.
Lanyon BP, Weinhold TJ, Langford NK, Barbieri M, James DFV et al. Experimental demonstration of a compiled version of Shor’S algorithm with quantum entanglement. Phys Rev Lett 2007; 99: 250505.
Politi A, Matthews JCF, O’Brien JL . Shor’s quantum factoring algorithm on a photonic chip. Science 2009; 325: 1221.
Martín-López E, Laing A, Lawson T, Alvarez R, Zhou XQ et al. Experimental realization of Shor’s quantum factoring algorithm using qubit recycling. Nat Photonics 2012; 6: 773–776.
Zhou XQ, Kalasuwan P, Ralph TC, O’Brien JL . Calculating unknown eigenvalues with a quantum algorithm. Nat Photonics 2013; 7: 223–228.
Giustina M, Versteegh MAM, Wengerowsky S, Handsteiner J, Hochrainer A et al. Significant-loophole-free test of bell’s theorem with entangled photons. Phys Rev Lett 2015; 115: 250401.
Shalm LK, Meyer-Scott E, Christensen BG, Bierhorst P, Wayne MA et al. Strong loophole-free test of local realism. Phys Rev Lett 2015; 115: 250402.
Kruse R, Katzschmann F, Christ A, Schreiber A, Wilhelm S et al. Spatio-spectral characteristics of parametric down-conversion in waveguide arrays. New J Phys 2013; 15: 083046.
Solntsev AS, Setzpfandt F, Clark AS, Wu CW, Collins MJ et al. Generation of nonclassical biphoton states through cascaded quantum walks on a nonlinear chip. Phys Rev X 2014; 4: 031007.
Jin H, Liu FM, Xu P, Xia JL, Zhong ML et al. On-chip generation and manipulation of entangled photons based on reconfigurable lithium-niobate waveguide circuits. Phys Rev Lett 2014; 113: 103601.
Tanzilli S, De La Rue R, Tanzilli S, Martin A, Kaiser F et al. On the genesis and evolution of Integrated Quantum Optics. Laser Photonics Rev 2012; 6: 115–143.
Politi A, Cryan MJ, Rarity JG, Yu SY, O’Brien JL . Silica-on-silicon waveguide quantum circuits. Science 2008; 320: 646–649.
Pernice WHP, Schuck C, Minaeva O, Li M, Goltsman GN et al. High-speed and high-efficiency travelling wave single-photon detectors embedded in nanophotonic circuits. Nat Commun 2012; 3: 1325.
Schuck C, Guo X, Fan L, Ma X, Poot M et al. Quantum interference in heterogeneous superconducting-photonic circuits on a silicon chip. Nat Commun 2016; 7: 10352.
Sharping JE, Lee KF, Foster MA, Turner AC, Schmidt BS et al. Generation of correlated photons in nanoscale silicon waveguides. Opt Express 2006; 14: 12388–12393.
Clemmen S, Huy KP, Bogaerts W, Baets RG, Emplit P et al. Continuous wave photon pair generation in silicon-on-insulator waveguides and ring resonators. Opt Express 2009; 17: 16558–16570.
Silverstone JW, Bonneau D, Ohira K, Suzuki N, Yoshida H et al. On-chip quantum interference between silicon photon-pair sources. Nat Photonics 2014; 8: 104–108.
Harris NC, Grassani D, Simbula A, Pant M, Galli M et al. Integrated source of spectrally filtered correlated photons for large-scale quantum photonic systems. Phys Rev X 2014; 4: 041047.
Collins MJ, Xiong C, Rey IH, Vo TD, He J et al. Integrated spatial multiplexing of heralded single-photon sources. Nat Commun 2013; 4: 2582.
Matsuda N, Le Jeannic H, Fukuda H, Tsuchizawa T, Munro WJ et al. A monolithically integrated polarization entangled photon pair source on a silicon chip. Sci Rep 2012; 2: 817.
Grassani D, Azzini S, Liscidini M, Galli M, Strain MJ et al. Micrometer-scale integrated silicon source of time-energy entangled photons. Optica 2015; 2: 88–94.
Silverstone JW, Santagati R, Bonneau D, Strain MJ, Sorel M et al. Qubit entanglement between ring-resonator photon-pair sources on a silicon chip. Nat Commun 2015; 6: 7948.
Guo X, Zou CL, Tang HX . 70 dB long-pass filter on a nanophotonic chip. Opt Express 2016; 24: 21167–21176.
Xiong C, Pernice WHP, Sun XK, Schuck C, Fong KY et al. Aluminum nitride as a new material for chip-scale optomechanics and nonlinear optics. New J Phys 2012; 14: 095014.
Pernice WHP, Xiong C, Schuck C, Tang HX . Second harmonic generation in phase matched aluminum nitride waveguides and micro-ring resonators. Appl Phys Lett 2012; 100: 223501.
Yang ZS, Sipe JE . Generating entangled photons via enhanced spontaneous parametric downconversion in AlGaAs microring resonators. Opt Lett 2007; 32: 3296–3298.
Schuck C, Pernice WHP, Tang HX . Waveguide integrated low noise NbTiN nanowire single-photon detectors with milli-Hz dark count rate. Sci Rep 2013; 3: 1893.
Levy JS, Foster MA, Gaeta AL, Lipson M . Harmonic generation in silicon nitride ring resonators. Opt Express 2011; 19: 11415–11421.
Schuck C, Pernice WHP, Ma X, Tang HX . Optical time domain reflectometry with low noise waveguide-coupled superconducting nanowire single-photon detectors. Appl Phys Lett 2013; 102: 191104.
Förtsch M, Schunk G, Fürst JU, Strekalov D, Gerrits T et al. Highly efficient generation of single-mode photon pairs from a crystalline whispering-gallery-mode resonator source. Phys Rev A 2015; 91: 023812.
Förtsch M, Fürst JU, Wittmann C, Strekalov D, Aiello A et al. A versatile source of single photons for quantum information processing. Nat Commun 2013; 4: 1818.
Reimer C, Caspani L, Clerici M, Ferrera M, Kues M et al. Integrated frequency comb source of heralded single photons. Opt Express 2014; 22: 6535–6546.
Clausen C, Bussières F, Tiranov A, Herrmann H, Silberhorn C et al. A source of polarization-entangled photon pairs interfacing quantum memories with telecom photons. New J Phys 2014; 16: 093058.
Blauensteiner B, Herbauts I, Bettelli S, Poppe A, Hübel H . Photon bunching in parametric down-conversion with continuous-wave excitation. Phys Rev A 2009; 79: 063846.
Christ A, Laiho K, Eckstein A, Cassemiro KN, Silberhorn C . Probing multimode squeezing with correlation functions. New J Phys 2011; 13: 033027.
Hu JY, Yu B, Jing MY, Xiao LT, Jia ST et al. Experimental quantum secure direct communication with single photons. Light Sci Appl 2016; 5: e16144 doi:10.1038/lsa.2016.144.
Reithmaier G, Kaniber M, Flassig F, Lichtmannecker S, Müller K et al. On-chip generation, routing, and detection of resonance fluorescence. Nano Lett 2015; 15: 5208–5213.
Lundskog A, Hsu CW, Fredrik KK, Amloy S, Nilsson D et al. Direct generation of linearly polarized photon emission with designated orientations from site-controlled InGaN quantum dots. Light Sci Appl 2014; 3: e139 doi:10.1038/lsa.2014.20.
Bettelli S . Comment on ‘Coherence measures for heralded single-photon sources’. Phys Rev A 2010; 81: 037801.
Rath P, Kahl O, Ferrari S, Sproll F, Lewes-Malandrakis G et al. Superconducting single-photon detectors integrated with diamond nanophotonic circuits. Light Sci Appl 2015; 4: e338 doi:10.1038/lsa.2015.111.
Zhang J, Itzler MA, Zbinden H, Pan JW . Advances in InGaAs/InP single-photon detector systems for quantum communication. Light Sci Appl 2015; 4: e286 doi:10.1038/lsa.2015.59.
Spring JB, Salter PS, Metcalf BJ, Humphreys PC, Moore M et al. On-chip low loss heralded source of pure single photons. Opt Express 2013; 21: 13522–13532.
Cao DY, Liu BH, Wang Z, Huang YF, Li CF et al. Multiuser-to-multiuser entanglement distribution based on 1550 nm polarization-entangled photons. Sci Bull 2015; 60: 1128–1132.
Zheng C, Long GF . Quantum secure direct dialogue using Einstein-Podolsky-Rosen pairs. Sci China Phys Mech Astron 2014; 57: 1238–1243.
Wang C, Burek MJ, Lin Z, Atikian HA, Venkataraman V et al. Integrated high quality factor lithium niobate microdisk resonators. Opt Express 2014; 22: 30924–30933.
Lin JT, Xu YX, Fang ZW, Wang M, Song JX et al. Fabrication of high-Q lithium niobate microresonators using femtosecond laser micromachining. Sci Rep 2015; 5: 8072.
Acknowledgements
HXT acknowledges support from a Packard Fellowship in Science and Engineering. CS acknowledges financial support from the Deutsche Forschungsgemeinschaft (SCHU 2871/2-1). Facilities used for fabrication were supported by Yale SEAS cleanroom and Yale Institute for Nanoscience and Quantum Engineering. The authors thank Michael Power and Michael Rooks for assistance in device fabrication.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Guo, X., Zou, Cl., Schuck, C. et al. Parametric down-conversion photon-pair source on a nanophotonic chip. Light Sci Appl 6, e16249 (2017). https://doi.org/10.1038/lsa.2016.249
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2016.249
Keywords
This article is cited by
-
Nonlinear and quantum photonics using integrated optical materials
Nature Reviews Materials (2024)
-
Large second-order susceptibility from a quantized indium tin oxide monolayer
Nature Nanotechnology (2024)
-
Ultra-efficient generation of time-energy entangled photon pairs in an InGaP photonic crystal cavity
Communications Physics (2023)
-
Quantum frequency conversion and single-photon detection with lithium niobate nanophotonic chips
npj Quantum Information (2023)
-
On-chip parallel processing of quantum frequency comb
npj Quantum Information (2023)