Abstract
Optical selection rules fundamentally determine the optical transitions between energy states in a variety of physical systems, from hydrogen atoms to bulk crystals such as gallium arsenide. These rules are important for optoelectronic applications such as lasers, energy-dispersive X-ray spectroscopy, and quantum computation. Recently, single-layer transition metal dichalcogenides have been found to exhibit valleys in momentum space with nontrivial Berry curvature and excitons with large binding energy. However, there has been little study of how the unique valley degree of freedom combined with the strong excitonic effect influences the nonlinear optical excitation. Here, we report the discovery of nonlinear optical selection rules in monolayer WS2, an important candidate for visible 2D optoelectronics because of its high quantum yield and large direct bandgap. We experimentally demonstrated this principle for second-harmonic generation and two-photon luminescence (TPL). Moreover, the circularly polarized TPL and the study of its dynamics evince a sub-ps interexciton relaxation (2p → 1s). The discovery of this new optical selection rule in a valleytronic 2D system not only considerably enhances knowledge in this area but also establishes a foundation for the control of optical transitions that will be crucial for valley optoelectronic device applications such as 2D valley-polarized THz sources with 2p–1s transitions, optical switches, and coherent control for quantum computing.
Similar content being viewed by others
Introduction
An optical selection rule is a fundamental principle dictating allowed and forbidden transitions. It is strictly imposed by various symmetries, such as temporal translational, spatial translational, and rotational symmetry, and their corresponding laws of conservation of energy, momentum, and angular momentum according to Noether’s theorem. In particular, the angular momentum contributed by an electron’s orbit and spin is important for revealing the symmetry of electronic states in atoms using atomic emission spectroscopy, controlling the polarization of semiconductor light-emitting diodes and lasers, and optically manipulating spin polarization in spintronics1,2. In conventional selection rule studies of solids such as bulk gallium arsenide and their quantum wells, the angular momenta of Bloch electrons are believed to be inherited exclusively from their atomic orbits3. Because of the requirement of inversion symmetry breaking and optical transitions off the center of the Brillouin zone4, the role of intercellular electron motion in selection rules received little attention until the recent discovery of valley angular momentum (VAM) in transition metal dichalcogenide (TMDC) monolayers, which have a direct bandgap at the edge of the Brillouin zone and lack inversion symmetry5,6,7,8.
The VAM is associated with energy valleys in momentum space in TMDC monolayers. The inversion symmetry breaking makes it possible for the VAM of Bloch electrons to include contributions from not only individual atomic orbits but also the circulation of electrons from one atomic site to another throughout the crystal unit cell. Bloch electrons in adjacent valleys have VAMs with opposite signs and follow a valley-dependent optical selection rule in the linear spectrum5,6,7. Recent studies have reported that monolayer WS2 exhibits a strong excitonic effect due to reduced dielectric screening9,10,11,12,13,14,15. The high quantum yield and large direct bandgap of WS2 are also important for future 2D optoelectronics in the visible range16. Similar to the hydrogen atom, an exciton confined in a 2D plane also possesses an excitonic angular momentum (EAM) resulting from the orbital motion of the electron relative to the hole. Although valley-dependent second-harmonic generation (SHG) and two-photon luminescence (TPL) in the near-infrared region have been recently observed in monolayer WSe217,18, direct observations of how the EAM and VAM determine nonlinear optical processes in the visible range are still lacking. Here, we report nonlinear optical selection rules based on the valley-exciton locked relationship imposed by the EAM and VAM combined in monolayer WS2. In addition, we studied the TPL dynamics in TMDC monolayers for the first time and demonstrated a sub-ps 2p–1s exciton relaxation involving phonons. These new selection rules and interexciton relaxation (2p–1s) in this 2D system not only are of fundamental importance in determining optical transitions and encoding information in valleytronics19 with multiple excitonic degrees but also provide important guidance for the design of future 2D THz sources and optical switches.
Materials and methods
Monolayer WS2 samples were mechanically exfoliated onto 275 nm SiO2/Si substrates from chemical vapor transport synthetic crystal flakes (2D Semiconductors Inc., Scottsdale, USA). The exfoliated monolayers were typically 5–10 micrometers in size and were characterized using tools such as atomic force microscopy and Raman and photoluminescence spectroscopy. The excitation light was extracted using an optical parametric oscillator (Inspire HF 100, Spectra Physics, Santa Clara, USA) pumped by a mode-locked Ti:sapphire oscillator. The laser pulse width was approximately 200 fs, and the repetition rate was 80 MHz. The excitation laser was linearly polarized by a 900–1300 nm polarizing beamsplitter. The transmitted p-polarized laser light was converted into circularly polarized light via a broadband Fresnel Rhomb quarter-wave retarder. The low-temperature experiment was performed in a continuous-flow liquid helium cryostat equipped with a 50× objective with a long working distance. The emission signal was detected in the backscattering configuration, analyzed using the Fresnel Rhomb quarter-wave retarder followed by a visible-range polarizer, and finally collected by a cooled CCD spectrometer. For time-resolved one-photon and two-photon photoluminescence spectroscopy, the signal passing through a bandpass filter with a bandwidth of 30 meV was collected by a Hamamatsu synchroscan streak camera with an overall time resolution of 2 ps. The transmissivity of the optical system was carefully calibrated to evaluate the absolute power level at the focusing plane. The emission spectra were normalized to the square of the focused power, as the excitation was limited to the unsaturated regime. The laser pulse width was measured using a home-built autocorrelator at the focus throughout the scanning range.
Results and discussion
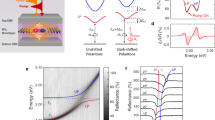
The three-fold rotational symmetry in monolayer WS2 requires total angular momentum conservation during light–matter interactions, in which the VAM, EAM, lattice angular momentum, and photon spin angular momentum are exchanged with each other. Induced by the local atomic orbital angular momentum and nontrivial Berry curvature distribution, the VAM has an out-of-plane component in both the conduction (τ ħ = 1ħ or −1ħ at K′ or K valleys, respectively) and valence (τ ħ = 0ħ at K′ or K valleys) bands. Meanwhile, the relative electron–hole motion is confined to a 2D plane, resulting in an exciton wavefunction in the form of Rn,l(ρ)eilφ with only an out-of-plane lħ EAM, where φ is the azimuthal angle and ρ is the electron–hole distance20,21. The out-of-plane VAM and EAM are combined collinearly. In addition, the crystal transforms the impinging angular momentum into a modulus of three by absorbing the excess angular momentum into the lattice, in a manner similar to the Umklapp process in phonon scattering22,23. As a result, under normally incident light, the conservation of out-of-plane angular momentum yields the following optical selection rule for the unique VAM and EAM in monolayer WS2:

Upon absorption, the change in the spin angular momentum of the photons, Δmħ, results in changes in the angular momenta of the valley (Δτħ), exciton (Δlħ) and crystal lattice (3Nħ). Although strong spin-orbit coupling is present, the spin of the electron does not flip under the dominant electric dipole transition. Therefore, the unchanged out-of-plane spin angular momentum makes no contribution to Equation (1).
Clearly, both the TPL and SHG processes exhibit a valley-exciton locked selection rule as described by Equation (1), meaning that excitonic resonant two-photon processes occur only within specific valleys under pure σ+, or σ− excitation. For example, in the 1s resonant SHG process, the transition from the ground state to the 1s state at a K valley requires a −1ħ VAM change and a 0ħ EAM change. According to Equation (1), this can occur only through the absorption of two pure σ+ fundamental photons with 2ħ and the emission of the excess 3ħ angular momentum into the crystal lattice. The virtual 1s exciton in the K valley immediately emits a σ− second-harmonic (SH) photon (Figure 1a). Under time reversal, only σ− fundamental photons can trigger the transition from the ground state to the 1s state at a K′ valley, leading to the emission of a σ+ SH photon in the resonant SHG process. Therefore, SHG emission always has the opposite helicity from that of the incident light. In regard to 2p resonant TPL, only the transition from the ground state to the 2p+ state with an EAM of +1ħ at a K′ valley is induced under pure σ+ excitation. In this transition, the required +1ħ VAM and +1ħ EAM changes can be satisfied only by the absorption of two σ+ fundamental photons without any lattice contribution. The 2p exciton from the above transition relaxes to the 1s state and finally emits a σ+ photon (Figure 1b). Again governed by Equation (1), in the case of σ− excitation, only TPL in a K valley occurs under time reversal. In contrast to the SHG case, 2p resonant TPL emission always exhibits the same helicity as that of the incident light. In Table 1, we provide a complete summary of the allowed and forbidden TPL and SHG transitions from the ground state to excitonic states with a strong optical response under pure circularly polarized incident light. In the following, we report polarization-resolved SHG and TPL spectral experiments that were performed to confirm this valley-exciton locked selection rule.
Schematic diagram of optical selection rules based on valley-exciton locking in 2D TMDC. (a) 1s exciton-resonant SHG in K′ and K valleys. Pumped by a σ+ (or σ−) polarized fundamental photon, an electron in the valence band at a K (or K′) valley reaches a virtual state. Within the lifetime of the virtual state, a second σ+ (or σ−) photon pumps the electron from the virtual state to the real 1s state in the K (or K′) valley. Immediately, a second-harmonic photon with a σ− (or σ+) polarization is emitted. (b) 2p exciton-resonant TPL in K′ and K valleys. Under two-photon excitation by σ+ (or σ−) polarized photons, the system transitions from the ground state to the real 2p+ (or 2p−) state with a change of +1ħ (or −1ħ) in the EAM at a K′ (or K) valley through an intermediate virtual state. The 2p exciton relaxes to the 1s excitonic state and emits a σ+ (or σ−) photon. The conduction band continuum and valence band continuum are labeled as CBC and VBC, respectively. The solid lines represent real excitonic states, and the dashed lines represent virtual states. Red indicates σ+ polarization; blue indicates σ− polarization. (c) Typical emission spectrum of monolayer WS2 pumped by a 1.14 eV laser pulse at 20 K. The peaks at 2.09 eV and 2.05 eV correspond to the 1s state of “A” neutral exciton and corresponding charged exciton (trion) created via TPL. The inversion symmetry breaking in monolayer WS2 results in an SHG signal at 2.28 eV. In the inset, the power dependences of the TPL and SHG emissions are plotted, exhibiting quadratic behavior.
WS2 monolayer samples were mechanically exfoliated onto SiO2/Si substrates (Supplementary Fig. S1). A typical light emission spectrum under excitation at 1090 nm (1.14 eV) and 20 K by an ultrafast laser is shown in Figure 1c. One emission peak, at 2.28 eV, is assigned to SHG. The other two peaks observed at 2.09 eV and 2.05 eV correspond to the neutral and charged exciton emissions. The charged exciton emission is dominant and was selected as our TPL signal. These excitonic emitted photon energies are nearly two times higher than that of the excitation photon, and therefore, they can originate only from two-photon absorption. This conclusion is further confirmed in the inset to Figure 1c. Both the TPL and the SHG exhibit a quadratic power dependence, indicating their two-photon nature.
According to Equation (1), SHG emissions carry the opposite helicity from that of the incident light, whereas TPL emissions display the same helicity. We first experimentally examined the optical selection rule for SHG. An excitation energy scan of the SHG signal (Figure 2a) revealed a resonance at 2.09 eV, indicating exciton-enhanced SHG due to the 1s state. The magnitude of the SHG signal at the 1s resonance is enhanced by nearly one order of magnitude compared with that under non-resonant excitation. We then measured the SHG under σ+ excitation (Figure 2b) at the 1s resonance. The SHG helicity, defined as  , was found to be −99% at an excitation energy of 1.045 eV. The negative sign here indicates that the SHG has the opposite circular polarization from that of the fundamental light. Determined by the selection rule, such a high helicity value is preserved because SHG is an instantaneous process and free of any intervalley scattering processes24. The observations of nearly 100% negative helicity and intensity resonance in SHG are well consistent with the proposed valley-exciton locked selection rule.
, was found to be −99% at an excitation energy of 1.045 eV. The negative sign here indicates that the SHG has the opposite circular polarization from that of the fundamental light. Determined by the selection rule, such a high helicity value is preserved because SHG is an instantaneous process and free of any intervalley scattering processes24. The observations of nearly 100% negative helicity and intensity resonance in SHG are well consistent with the proposed valley-exciton locked selection rule.
Experimental observation of the SHG selection rule in monolayer WS2 at 20 K. (a) SHG intensity (black dots) versus SHG excitation energy in a scan from 0.97 eV to 1.19 eV. A dominant SHG intensity peak is observed at a pump energy of 1.045 eV, which is attributable to the 1s resonance. (b) Polarization-resolved SHG measurements for σ+ (red curve) and σ− (black curve) detection under pumping by σ+. A negative helicity of P = −99.0% ± 0.1% was observed from multiple repeated measurements. The excitation energy was 1.045 eV. The significant negative helicity at the 1s resonance confirms the existence of a rigorous selection rule for SHG.
In contrast to the SHG selection rule at the 1s resonance, TPL displays a completely opposite valley-dependent selection rule at the 2p resonance. In an excitation energy scan (Figure 3a), a dominant resonance was observed at 1.13 eV, corresponding to the 2p excitonic peak. Compared with the 1s excitonic level, the 2p exciton has a greater linewidth (∼80 meV) and an asymmetric shape. To test the selection rule, we measured the TPL spectrum under σ+ light excitation (Figure 3b). The TPL helicity was measured to be 29.6% at the excitation energy (1.13 eV) and had the same sign as that of the incident light. The helicity changed sign when the monolayer was pumped with σ− light (see Supplementary Fig. S2). More interestingly, we observed a TPL resonance in the emission helicity at the 2p peak (Figure 3b inset), confirming our theory that the EAM imposes an additional selection rule on the optical transition. The relatively low helicity value observed here is due to the strong intervalley scattering upon the injection of such high energies25. Away from the 2p resonance peak, we always observed nonzero TPL with lower energy excitation, as shown in Figure 3a, indicating the presence of several non-excitonic states with p components below the 2p state. This background cannot originate from the re-absorption of the SHG emission because the emission helicity is positive.
Experimental observation of the TPL selection rule in monolayer WS2 at 20 K. (a) TPL intensity versus TPL excitation energy in a scan from 1.06 eV to 1.19 eV. A dominant TPL intensity peak resonance is observed under 1.13 eV laser pulse excitation, which is attributable to the 2p resonance. (b) Polarization-resolved TPL measurements for σ+ (red curve) and σ− (black curve) detection under σ+ light excitation. A circular polarization of P = 29.6% ± 0.5% was observed based on multiple repeated measurements. The excitation energy was 1.13 eV. The inset plots the TPL helicity versus the TPL excitation energy for a scan of the same range under excitation by σ+ polarized light. A helicity resonance is observed at the 2p excitonic level. Away from the 2p resonance, the TPL helicity decreases with increasing excitation energy due to the energy-dependent intervalley scattering.
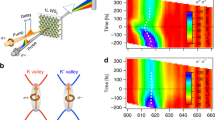
Subsequently, we further examined the valley-exciton locked selection rule by performing time-resolved TPL measurements. After the initial two-photon absorption and the formation of 2p valley excitons, two subsequent processes occur: the 2p excitons relax to 1s excitons, and these 1s excitons recombine. If the populations in the K and K′ valleys are unbalanced, intervalley scattering will occur. Here, we conducted time-resolved TPL measurements at the 2p resonance, and the signal was detected by a synchroscan streak camera with an overall time resolution of 2 ps. Under linearly polarized excitation light, the intervalley scattering has no net contribution because the populations in both types of valleys are equal. Therefore, the time-resolved TPL trace includes only relaxation and recombination (Figure 4a). The rising edge after excitation is predominantly associated with the relaxation process from 2p to 1s26, whereas the recombination process is reflected by the decaying portion of the curve. To capture the essence of the dynamics, we used a three-level rate equation (Supplementary Information and Supplementary Fig. S3). Typically, a process no shorter than one tenth of the system’s time resolution can be extracted by applying convolution fitting with the instrument response function (IRF)27,28. In this manner, we can infer that the interexciton relaxation time is τ2p–1s = 600 ± 150 fs and that the recombination time is τrec = 5.0 ± 0.2 ps. Regarding the sub-ps 2p–1s relaxation, which is reported here in 2D TMDC for the first time, it was further verified by time-resolved PL measurements under near-resonance one-photon excitation (Figure 4b). The rising feature in this curve is much sharper compared with that under 2p resonant two-photon excitation, which indicates more rapid relaxation because of a smaller energy gap. Indeed, our fit shows that the relaxation time to the 1s exciton edge in this case is less than 200 fs (the fastest process can be extracted from convolution fitting). This confirms our observation of a measurable sub-ps 2p–1s relaxation due to the large energy gap between the 2p and 1s excitonic levels. Excited carrier relaxation can typically follow three possible pathways: carrier–carrier scattering, carrier–phonon scattering, and radiative emission. Carrier–carrier scattering is predominantly dependent on carrier density. However, as we varied the pump intensity, no significant change in the dynamics was observed (see Figure 4c). Therefore, carrier–carrier scattering is unlikely to account for the sub-ps relaxation here. Meanwhile, radiative emission from the 2p–1s transition can be excluded because the transition rate is not expected to be as fast as the sub-ps level. Given the comparable densities of states and transition matrix amplitudes calculated using the GW method9,21, one should expect the 2p–1s transition time to be similar to the 1s exciton radiative lifetime. Because the radiative lifetime of the 1s exciton is approximately 100 ps in our case (the quantum yield is ∼5%, and the lifetime of the nonradiative decay is 5 ps, as shown in Figure 4a), the sub-ps relaxation we observed cannot be radiative decay. Therefore, it is very likely to be attributable to exciton–phonon scattering. This is further confirmed by the broader linewidth of the 2p exciton (see Figure 3a). Under the assumption that the 2p–1s relaxation is accomplished via optical phonon cascade scattering, each phonon scattering event requires ∼130 fs (the energy gap between the 2p and 1s levels is 220 meV, and the dominant optical phonons observed via Raman spectroscopy have energies of 44 meV for the E2g mode and 51 meV for the A1g mode). According to the uncertainty principle, this corresponds to an additional linewidth broadening of greater than 30 meV compared with the 1s exciton. This is consistent with our observation, which indicates 40 meV of additional broadening. It is suspected that a 1s hot exciton with some kinetic energy is generated after a 2p exciton collides with a phonon and cascades to the 1s exciton edge. The rapid recombination observed at the 1s exciton edge (τrec = 5.0 ± 0.2 ps) is likely attributable to nonradiative recombination, such as defect trapping or a phonon-assisted process29. This is confirmed by the quantum yield measurement18, which indicates a quantum yield of approximately 5%. We carefully checked that the nonradiative channel is not dependent on the excitation power (Figure 4c), which excludes any exciton–exciton annihilation mechanism30.
Time-resolved valley exciton dynamics in monolayer WS2 at 20 K. (a) Time trace of the TPL (red curve) excited by a linearly polarized laser pulse at 1.13 eV. Compared with the instrument response function (IRF), presented as the blue curve, the TPL time trace exhibits observable rising and decaying features. Based on our three-level rate equation model (see the Supplementary Information), the results of convolution fitting (black curve) indicate an interexciton relaxation time τ2p−1s of 600 ± 150 fs and a recombination time τrec of 5.0 ± 0.2 ps. (b) Relaxation dynamics comparison. The time-resolved relaxation curves (rising features) for two-photon-induced PL (TPL, black curve) and one-photon-induced PL (blue curve) are plotted. The one-photon-induced PL, excited near the resonance at 2.10 eV, exhibits a sharper rising feature compared with that of the TPL excited at the 2p resonance (2.26 eV). This difference confirms that the relaxation of the 2p exciton requires a longer time because of the larger energy gap. Here, the red curve represents the IRF. (c) Power-dependent time-resolved 2p resonant TPL. TPL time traces recorded under pumping by a laser pulse at 1.13 eV with different incident powers. The power was varied over one order of magnitude, resulting in a change in the exciton population of two orders of magnitude. No significant change in the dynamics is observed in this power range, thereby excluding exciton–exciton annihilation. (d) Polarization-resolved time traces of the TPL excited by σ+ polarized light at 1.13 eV. Because of the selection rule and intervalley scattering, the σ+ emission (red curve) displays a greater intensity and more rapid decay than does the σ− emission (black curve). The blue and green dashed lines are guides for the eye. The inset shows the convolution fit (purple curve) for the time-resolved valley exciton population (σ+ − σ−, black dots). The intervalley scattering times during relaxation, τinter(2p–1s), and recombination, τinter(1s), are estimated to be 3 ± 1 ps and 8.3 ± 0.5 ps. The error ranges were obtained from fitting to the results of multiple repeated measurements. PL, photoluminescence.
For σ+ two-photon excitation at the 2p resonance, the dynamical curves for emission at the different polarizations are shown in Figure 4d. The σ+ TPL from the K′ valleys exhibits a higher intensity than that of the σ− TPL from the K valleys, which again confirms the valley-exciton locked selection rule. Compared with the σ+ emission, the σ− emission always undergoes slower decay until the populations in the two types of valleys are equal. This difference in the decay trend results from intervalley scattering, which tends to equalize the exciton populations in the two valleys. From convolution fitting with the IRF and recombination time, we can estimate the lifetimes of intervalley scattering during relaxation, τinter(2p−1s), and recombination, τinter(1s), to be 3 ± 1 ps and 8.3 ± 0.5 ps, respectively (Figure 4d inset). The exchange interaction between the electron and hole can induce both a spin flip and a momentum change via Coulomb potential scattering. Recent calculations show that this process can occur in the picosecond range and becomes more efficient when the exciton carries more energy31, which may account for the rapid depolarization observed in our measurements.
Conclusion
In summary, we discovered nonlinear optical selection rules based on valley-exciton locking in monolayer WS2. This important finding reveals that the EAM and VAM combined fundamentally determine the optical transitions in TMDC monolayers. These new selection rules together with the observed interexciton dynamics offer important guidance for the manipulation of exciton and valley degrees of freedom in 2D TMDC. For example, the well-defined excitonic levels located in distinguishable valleys could encode quantum information, potentially leading to the design of THz sources with 2p–1s transitions, optical switches and quantum interference control based on this 2D material32,33,34.
Authors’ contributions
JX, YW, and HZ prepared the samples. JX performed the measurements. JX, ZY, YW, HZ and YW conducted the data analysis. XZ guided the research. All authors contributed to the preparation of the manuscript.
References
Hilton DJ, Tang CL . Optical orientation and femtosecond relaxation of spin-polarized hole in GaAs. Phys Rev Lett 2002; 89: 146601.
Gerardot BD, Brunner D, Dalgarno PA, Öhberg P, Seidl S et al. Optical pumping of a single hole spin in a quantum dot. Nature 2008; 451: 441–444.
Chuang SL . Physics of Photonic Devices. Hoboken, NJ: Wiley; 2009.
Yao W, Xiao D, Niu Q . Valley-dependent optoelectronics from inversion symmetry breaking. Phys Rev B 2008; 77: 235406.
Mak KF, He K, Shan J, Heinz TF . Control of valley polarization in monolayer MoS2 by optical helicity. Nat Nanotechnol 2012; 7: 494–498.
Cao T, Wang G, Han WP, Ye HQ, Zhu CR et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nat Commun 2012; 3: 887.
Zeng HL, Dai JF, Yao W, Xiao D, Cui XD . Valley polarization in MoS2 monolayers by optical pumping. Nat Nanotechnol 2012; 7: 490–493.
Liu GB, Xiao D, Yao YG, Xu XD, Yao W . Electronic structures and theoretical modelling of two-dimensional group-VIB transition metal dichalcogenides. Chem Soc Rev 2015; 44: 2643–2663.
Ye ZL, Cao T, O’Brien K, Zhu HY, Yin XB et al. Probing excitonic dark states in single-layer tungsten disulphide. Nature 2014; 513: 214–218.
Baugher BWH, Churchill HOH, Yang YF, Jarillo-Herrero P . Optoelectronic devices based on electrically tunable p-n diodes in a monolayer dichalcogenide. Nat Nanotechnol 2014; 9: 262–267.
Mak KF, McGill KL, Park J, McEuen PL . The valley Hall effect in MoS2 transistors. Science 2014; 344: 1489–1492.
He KL, Kumar N, Zhang L, Wang ZF, Mak KF et al. Tight bound excitons in monolayer WSe2 . Phys Rev Lett 2014; 113: 026803.
Chernikov A, Berkelbach TC, Hill HM, Rigosi A, Li Y et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2 . Phys Rev Lett 2014; 113: 076802.
Zhu BR, Chen X, Cui XD . Exciton binding energy of monolayer WS2 . Sci Rep 2015; 5: 9218.
Lin YX, Ling X, Yu LL, Huang SX, Hsu AL et al. Dielectric screening of excitons and trions in single-layer MoS2 . Nano Lett 2014; 14: 5569–5576.
Ye Y, Wong ZJ, Lu XF, Zhu HY, Chen XH et al. Monolayer excitonic laser. 2015; arXiv:1503.06141.
Wang G, Marie X, Gerber I, Amand T, Lagarde D et al. Giant enhancement of the optical second-harmonic emission of WSe2 monolayers by laser excitation at exciton resonances. Phys Rev Lett 2015; 114: 097403.
Seyler KL, Schaibley JR, Gong P, Rivera P, Jones AM et al. Electrical control of second-harmonic generation in a WSe2 monolayer transistor. Nat Nanotechnol 2015; 10: 407–411.
Behnia K . Condensed-matter physics: polarized light boosts valleytronics. Nat Nanotechnol 2012; 7: 488–489.
Zaslow B, Zandler ME . Two-dimensional analog to the hydrogen atom. Am J Phys 1967; 35: 1118–1119.
Qiu DY, da Jornada FH, Louie SG . Optical spectrum of MoS2: many-body effects and diversity of exciton states. Phys Rev Lett 2013; 111: 216805.
Simon HJ, Bloembergen N . Second-harmonic light generation in crystals with natural optical activity. Phys Rev 1968; 171: 1104–1114.
Bloembergen N . Conservation laws in nonlinear optics. J Opt Soc Am 1980; 70: 1429–1436.
Boyd RW . Nonlinear Optics. Burlington, MA: Academic Press; 2008.
Kioseoglou G, Hanbicki AT, Currie M, Friedman AL, Gunlycke D et al. Valley polarization and intervalley scattering in monolayer MoS2 . Appl Phys Lett 2012; 101: 221907.
Snoke DW, Rühle WW, Köhler K, Ploog K . Spin flip of excitons in GaAs quantum wells. Phys Rev B 1997; 55: 13789–13794.
Lakowicz JR . Topics in Fluorescence Spectroscopy Ch. 3. New York: Kluwer Academic Publishers; 2002.
Hong XP, Kim J, Shi SF, Zhang Y, Jin CH et al. Ultrafast charge transfer in atomically thin MoS2/WS2 heterostructures. Nat Nanotechnol 2014; 9: 682–686.
Shi HY, Yan RS, Bertolazzi S, Brivio J, Gao B et al. Exciton dynamics in suspended monolayer and few-layer MoS2 2D crystals. ACS Nano 2013; 7: 1072–1080.
Kumar N, Cui QN, Ceballos F, He DW, Wang YS et al. Exciton-exciton annihilation in MoSe2 monolayers. Phys Rev B 2014; 89: 125427.
Yu T, Wu MW . Valley depolarization due to intervalley and intravalley electron-hole exchange interactions in monolayer MoS2 . Phys Rev B 2014; 89: 205303.
Slavcheva G, Kavokin AV . Polarization selection rules in exciton-based terahertz lasers. Phys Rev B 2013; 88: 085321.
Fleischhauer M, Imamoglu A, Marangos JP . Electromagnetically induced transparency: optics in coherent media. Rev Mod Phys 2005; 77: 633.
Silberberg Y . Quantum coherent control for nonlinear spectroscopy and microscopy. Annu Rev Phys Chem 2009; 60: 277–292.
Acknowledgements
This work was supported by the “Light-Material Interactions in Energy Conversion” Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-AC02-05CH11231.
Note: Accepted article preview online 6 September 2015
Author information
Authors and Affiliations
Corresponding author
Additional information
Note: Supplementary information for this article can be found on the Light: Science & Applications' website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 Unported License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Xiao, J., Ye, Z., Wang, Y. et al. Nonlinear optical selection rule based on valley-exciton locking in monolayer ws2. Light Sci Appl 4, e366 (2015). https://doi.org/10.1038/lsa.2015.139
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2015.139
Keywords
This article is cited by
-
First-principles study of the electronic and optical properties of Ho\(_{\text{W}}\) impurities in single-layer tungsten disulfide
Scientific Reports (2022)
-
All-optical nonreciprocity due to valley polarization pumping in transition metal dichalcogenides
Nature Communications (2021)
-
Probing valley population imbalance in transition metal dichalcogenides via temperature-dependent second harmonic generation imaging
npj 2D Materials and Applications (2021)
-
All-optical polarization and amplitude modulation of second-harmonic generation in atomically thin semiconductors
Nature Photonics (2021)
-
Detection of electron-phonon coupling in two-dimensional materials by light scattering
Nano Research (2021)