Abstract
The surface plasmon resonance tracking over metal surfaces is a well-established, commercially available, biochemical quantification tool primarily applied in research. The utilization of such a tool is, however, constrained to highly specialized industries, capable of justifying the human and instrumental resource investments required by the characterization method. We have proposed to expand the field of application of this biosensing approach by redesigning this method through the integration and miniaturization within a semiconductor platform. Uncollimated and broadband emission from a light-emitting semiconductor is employed to couple a continuum of surface plasmon modes over a metal–dielectric architecture interfaced with a GaAs–AlGaAs substrate. A tensor version of rigorous coupled wave theory is employed to optimize the various fabrication specifications and to predict the light scatterings over a wide range of variables. We then present a hyperspectral characterization microscope capable of directly mapping the dispersion relation of scattered light, including diffracted surface plasmons, as an intensity distribution versus photon energy and surface wavevectors. Measurements carried out in a buffered solution demonstrate the accurate description of the uncollimated and broadband surface plasmon states. Finally, we introduce a simplified method of dispersion mapping, in which quasi-conic cross-sections of the light's scattering can be acquired directly, thus monitoring surficial responses in as fast as 1.2 s. This is over 300 times faster than required by implementing full dispersion mapping. While compromising on the volume of collected information, this method, combined with the solid-state integration of the platform, shows great promise for the fast detection of biochemical agents.
Similar content being viewed by others
Introduction
Surface plasmon resonance (SPR) is a well-established and easy-to-induce phenomenon enabling the study of surficial optical properties, such as those related to the alterations of the local dielectric constants. The resonance tracking of the surface plasmon (SP) coupling has already found a wide range of applications, especially in the field of biochemical analysis, where SPR systems are employed to determine the concentration of molecules and kinetics of intermolecular interactions.1 Using proper stabilization and correction procedures, it has been demonstrated that the SPR technique can be used to detect biochemical fluctuations inducing refractive index changes lower than 10−8 refractive index unit.2 The same approach can also be employed for the spatial imaging of binding events.3 However, the SPR technology has remained in the realm of trained professionals, in academic laboratories and within specialized industries, requiring relatively large space, capital investment and the support of qualified personnel.1 These restrict the possible range of contextual applications for the SPR technology, a platform that fundamentally does not need to be constrained by such parameters.
The initial objective of the presented research was to adapt the SPR platform in order to broaden its potential fields of applications. It is believed that one way to accomplish this technological democracy is through the modern advantage of nano optoelectronics, in order to develop an integrated semiconductor-based SPR device. We have proposed a general approach involving the utilization of light-emitting semiconductor architectures, such as quantum wells (QWs), as an embedded way to couple SPs.4 The SPs, interacting with the substances to be characterized, are then extracted through surface corrugation and imaged by a microscope. Thus re-engineered, an SPR microsystem would offer portability and drastic reduction in operational costs, consequently opening a potential for delocalized applications. Coupled with integrated electronic circuits, a preset SPR semiconductor chip would ideally be operated by the layperson.
A rethinking of traditional SPR system design into a wholly solid-state device inevitably involves a dislocation of the system's complexity from the user to the designer, along with compromises between applicability and sensitivity. The functioning of the proposed SPR device is intrinsically less straightforward than its traditional Kretschmann–Raether counterpart,5 but offers the potential to present simplified, pre-analysed output in a miniaturized semiconductor interface. We will therefore first present how we have developed a mathematical algorithm to design, predict and study the output of this novel approach.
As it will be shown, the most basic QW-SPR system developed is operating based on an embedded nanostructure that emits light in a relatively broadband and uncollimated way. The presented QW-SPR device serves as a generic platform for the scientific and technical study of SPR integration, e.g., for biosensing. As it will be presented, the broadband and uncollimated approach taken has practical tradeoffs. However, a complete understanding of the convoluted photonic phenomena in such simple integrated architecture does provide valuable insights for the potential development of future commercial plasmonic nanodevices.
In order to experimentally consider every possible case of QW-SPR operation, we have developed a new measurement tool based on hyperspectral imagery, enabling the collection of multidimensional SPR cubes equivalent to 108 traditional SPR experiments concurrently.6 Examples of QW-SPR hyperspectral measurements under biomolecular conditions are presented. This method allows the direct mapping of the dispersion of scattering events, in this case, the diffraction of SPs.
Once all the functioning mechanisms have been laid out, we present an initial step toward the downscaling of the dispersion measurement set-up (microscope). The quasi-hyperspectral measuring method greatly simplifies the conventional method of data collection and decreases acquisition time by a factor of over 300. This method enables the characterization of scattering events, through the recording of their projected dispersion relation, with time resolutions limited only by the light source intensity and camera speed.
Materials and methods
Theoretical analysis
A straightforward integration of the SPR technology with a light-emitting semiconductor is achieved by constructing a metal-dielectric interface atop the solid-state light emitting substrate,4,7 as shown in Figure 1. Through electroluminescence or photoluminescence (PL), the embedded QW is excited to emit radiation. For the most general case presented here, a GaAs–AlGaAs QW microstructure is employed. The emission is uncollimated (i.e., propagating in all directions) and the broadband spectral bandwidth exceeds 140 nm (1.38–1.65 eV). A dielectric spacer and metal layer are deposited by evaporation on the structure, thus enabling the support of SP modes. The metal layer can be corrugated in order to extract the SPs into the far field for imaging by a microscope. This top layer can also be biofunctionalized in various manners for specific experiments.
Cross-section of the architecture. SEM image of the surface corrugation employed to extract the SPs. A SiO2 layer (ε2) is deposited atop a light emitting semiconductor (ε1). A corrugated Au layer (ε3) is then evaporated so that the SPs modes can be extracted into PBS (ε4) and measured by the microscope. The inset illustrates the extraction of the SPs modes coupled at the Au-PBS interface (SP1) through the ±1st diffraction order. Figure taken from literature.6 PBS, phosphate-buffered saline; SEM, scanning electron microscopy; SP, surface plasmon.
The principle behind uncollimated and broadband SP coupling is detailed in Figure 2. A continuous range of incoming radiation from the QW encounters the metal layer at the dielectric interface. In Figure 2a, when the energy (E) and projected wavevectors (|kll|) of the incoming light meet the specific dispersion of the SPs supported by the interface, a resonance occurs with the surface electrons inducing the SPR.5 It is important to notice that the surface charge fluctuations can be coupled at any energy, through their corresponding |kll| (inset Figure 2a). Moreover, kll is composed of the two planar directions in  and
and  . Therefore, at a given energy, SPR can be induced for all the |kll| meeting kll=kSPR(E)=kx
. Therefore, at a given energy, SPR can be induced for all the |kll| meeting kll=kSPR(E)=kx +ky
+ky . This is shown in Figure 2b, where the device in Figure 1 can support a continuum of SP modes, whose dispersion relation in E(kx,ky) is a cone-like shape. To understand such system in detail, and to be able to design various architectures for specific applications, a very broad yet powerful analytical tool was required.
. This is shown in Figure 2b, where the device in Figure 1 can support a continuum of SP modes, whose dispersion relation in E(kx,ky) is a cone-like shape. To understand such system in detail, and to be able to design various architectures for specific applications, a very broad yet powerful analytical tool was required.
Uncollimated and broadband coupling of SPR. (a) For a given energy E, SP modes can be coupled at the metal-dielectric interface when the incident light has an in-plane wavevector kll=(kx2+ky2)½=kSPR(E), with the values of kSPR(E) depending on the architecture. (b) kSPR(E) can be coupled for a continuum of kll values, corresponding to a circle in the kx−ky plane. When varying the energy, a cone-like shape is constructed in the E(k) space, corresponding to the full dispersion relation of the SPR event taking place at the surface. This is occurring outside of the light cone klight=E/ħc. SP, surface plasmon; SPR, surface plasmon resonance.
The Green tensor approach was among the potential candidates; it is highly flexible in applications and allows an accurate description of the near field.8 It is thus an attractive tool for studying nano-antennas or specific perturbations by localized geometries in the local fields. The method is, however, relatively computer intensive and requires a pre-established knowledge of the architecture to work, i.e., it is an impractical development tool. Finite-difference time-domain or partial differential equation methods (such as COMSOL Multiphysics), are also powerful tools to study arbitrary shapes and resolving local phenomena. Commercial partial differential equation software programs have the additional advantage of offering an interface with other non-photonic physical problems. Nonetheless, they have the same disadvantage of being relatively CPU intensive, especially in order to avoid simulation cross-talk or to run a very large amount of simulations to find the optimal value of specific sets of parameters.9
One of the simplest ways to calculate the scattering distribution in a periodic structure such as one comparable to Figure 1, is through the application of the rigorous coupled wave analysis (RCWA) proposed by Glytsis and Gaylord10 and later optimized by many authors.11,12 In this method, all the diffraction orders are characterized by a pair of forward and backward flux transfer coefficients, much like the classical Fresnel coefficients for reflection and transmission. This method is relatively uncomplicated, robust, can account for arbitrary grating geometries and is capable of providing exact solutions for specific shapes. The RCWA method resolves the scattering distribution of a given photonic architecture configuration by generating set of solution matrices at any requested point in space (r), given specific light injection properties (energy, wavevector, polarization (P), etc.). Because of its great simplicity and robustness, we adapted this basic analytical tool into a research and development instrument. The matrix mathematics was replaced by tensor analyses, where tensorial dimensions are basically added for every device variables to be optimized. In other words, this tensorial RCWA allows the evaluation of the scattering distribution of a large preset of architectures, angular emissions, energies or spatial distributions. This tool enabled the complete customization of the integrated structures required for specific applications; in this case, the far field extraction of uncollimated and broadband SPR.
For the presented prototype, the SPR architecture comprises a GaAs–AlGaAs QW microstructure with the peak emission at 1.42 eV, a 722-nm SiO2 layer deposited through PECVD and a 20-nm continuous Au film with a Au grating of target periodicity P=669 nm, height 20 nm and lines/grooves ratio of 1.35. The physical properties of all the materials are determined experimentally.13 The QW-SPR measurements presented in this communication are taken in a phosphate-buffered saline (PBS) solution of pH=7.4, as a preparation for dynamic molecular studies. Figure 3 presents the calculated near field emission for this specific architecture, around the metal interface. Tensorial RCWA allows the examination of any diffraction order separately, or to combine them all, as in Figure 3, where the SPAu–PBS is coupled at 10.1 µm−1 and the at 12.6 µm−1 and diffracted at wavevectors kSPn≈kSP+nkG, with n denoting the diffraction order and kG the grating wavevector (approximately 2π/P). Figure 4a presents the predicted far field output of the device at a fixed energy (E=1.42 eV), for wavevectors within the light cone. Figure 4b shows a cross-section of the dispersion cone E(k) when ky≡0. In such a way, for any given integrated architecture, the full dispersion pattern distributed in intensity, I(E,k,r,P), can be evaluated. While these calculations do provide a complete description of the scattering behavior of any layered architecture,14 there was no existing experimental set-up that could be used to verify these predictions in their entirety, i.e., provide a full picture of the scattering in I(E,k). Because of the intricate relationship between E and k, most scattering experiments, including SPR, limit some dispersion parameters by either fixing the input energy with a laser or polar angle scanning5 or by fixing both while studying the azimuthal dependencies.15 Experimentally, measuring the whole I(E,k) scattering properties of an arbitrary object is a convoluted task.
Logarithm of the near field intensity distribution at the interface. Example of calculation using tensor RCWA, where a cross-section in z–kll is shown, thus illustrating the spatial distribution of the field for all the supported photonic modes. The intensity represents the ln|E|2 of the P-polarization for the described QW-SPR architecture in PBS solution at E=1.42 eV. PBS, phosphate-buffered saline; RCWA, rigorous coupled wave analysis; QW, quantum well; SPR, surface plasmon resonance.
Logarithm of the far field intensity distribution. (a) Calculated intensity distribution of ln|E|2 of the P-polarization for the described QW-SPR architecture in PBS solution at E=1.42 eV in the far field. The entire kx−ky plane is shown within the light cone. The SP modes diffracted through the ±1st order are visible. The color scale is the same as (b). (b) The same distribution of ln|E|2 is shown at ky=0 for the various energies emitted by the QW structure. QW, quantum well; SP, surface plasmon; SPR, surface plasmon resonance.
Experimental set-up
We were able to overcome the challenges presented by the complete characterization of the scattering properties I(E,k), through the use of hyperspectral technology. Hyperspectral imagery (HI) is a rising method for fast and accurate electromagnetic characterization, with applications ranging from carbon-nanotube characterization, astronomy, photovoltaic to the mining and dermatology industries.16 In those fields of application, the spatial distribution of broadband, or unknown, light emitters can be rapidly and accurately monitored through HI. The principle of HI revolves around the acquisition of a continuous stack of spectrally spread spatial (x,y) images, and then reconstituting a hyperspectral cube whose orthogonal dimensions correspond to an intensity distribution in I(E,x,y). For the specific application of PL or electroluminescence mapping of semiconductors, this technology allows excellent resolutions in all the studied dimensions while generating data in a much faster way than its classical counterparts (e.g., a commercial Philips PLM-150 luminescence mapper). It is thus appropriate to use HI as a platform for the experimental characterization of the QW-SPR microchips. The specific system resolution depends on the microscope objective's (MO) field of view employed, the selected camera size, binning and acquisition speed. For example, a 10× MO can generate a cube of [1 mm, 1.5 mm, 1.8 eV] in size with a resolution of [1 µm, 1 µm, 1.6×10−3 eV].
However, SPR events occur in the wavevector (angular) space, not in the x–y space. Therefore, we have adapted the HI system to allow the imaging of the conjugate plane of emission in kx–ky. To do so, a kinematic mirror can be used to cut the imaging path and elongate the system in such a way that the MO pupil is now projected on the camera and measured at various energies. Figure 5a presents a simplified sketch of this set-up. The resulting hyperspectral cubes are thus intensity distributed in I(E,kx,ky), directly yielding the dispersion of the light occurring within the MO field of view. In this manner, the physical properties of any scattering event can be monitored in quasi-real time. This type of technology could be employed for crystallography, surface metrology or speckle imagery; we use it here to monitor the various diffraction patterns out of the QW-SPR architectures, such as those predicted in Figures 3 and 4. The current system resolution is dependent on the MO numerical aperture (NA) and selected camera settings. For the measurements presented here, the acquisition range is typically [2.1 µm−1, 2.1 µm−1, 0.3 eV] with a maximum resolution of [1.3×10−3 µm−1, 1.3×10−3 µm−1, 1.6×10−3 eV] for the 10× MO employed (NA=0.3).
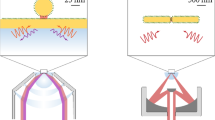
Hyperspectral imaging set-up. (a) The microscope objective collects light emitted from the surface scatterings. The collected light can then be sent directly to the VBG, which spectrally spreads the light onto the CCD in [x, y, E], to generate a spatial mapping of the surface. A kinetic mirror (double arrows) can also be activated in order to elongate the optical path length, thus projecting the conjugate space on the CCD to generate a dispersion mapping in [kx, ky, E]. The inset sketches what a rectified hyperspectral scan is for diffracted SPR. (b) Close-up of the hyperspectral scanning process, necessary for the understanding of conical SPR tracking. At any given position of the VBG (in conjugate mode), the projected space on the CCD is skewed: one axis still corresponds to kx, but the other one is a combination of E and ky. Imaging diffracted ‘cones’ of SPR in real-time results in elliptical projections in the [kx, E−ky] space. It is the collection and rectification of multiple cross-sections along the  axis that allows a full orthogonal [kx, ky, E] dispersion. CCD, charge-coupled device; SPR, surface plasmon resonance; VBG, volume Bragg grating.
axis that allows a full orthogonal [kx, ky, E] dispersion. CCD, charge-coupled device; SPR, surface plasmon resonance; VBG, volume Bragg grating.
Results and discussion
Hyperspectral SPR measurements
Figure 6 presents the PL intensity distribution over the emitted energies, and the inset shows the spatial distribution of the PL intensity emitted by the architecture at E=1.42 eV. The grating is made over a 1 mm×1 mm region and thicker metal is evaporated everywhere else in order to minimize light transmission from the non-grated areas. Note that the sample is in a PBS buffer solution.
Photoluminescence mapping of the semiconductor structure. The substrate emits a broadband signal which peaks at E=1.42 eV. A broader and more intense emission would yield stronger SNR for all the presented results. Inset: Cross-section of a hyperspectral spatial mapping of the 1 mm2 grating window at E=1.42 eV. PL, photoluminescence; SNR, signal-to-noise ratio.
When switching into the HI conjugate mode mapping, the collected cubes yield the intensity distribution in I(E,kx,ky). For example, a cross-section of this cube at fixed energy provides information on I(k), as in Figure 7a, where the SPAu–PBS mode is diffracted through the ±1st order. Given that NA=0.3, only a portion of the predicted far field output in Figure 4a is actually measured. Multiple cross-sections can be collected for a wide range of emitted energies. The SPR peak positioning in such HI cube can then be employed as a means to quantify the surficial refractive index changes. The resonance points for the SPs can be extracted for all the monitored E and k and thus directly quantifying the SPR dispersion at the metal surface. Figure 7b shows the SPR peak positions in the conjugate space at a given time, when the QW-SPR architecture is in the PBS solution. When dynamic studies are carried out, the variations in the SP dispersion relations can be tracked directly.
Hyperspectral mapping of the SP dispersion. (a) The normalized logarithm of the experimentally measured distribution of the luminescence in the kx−ky plane is shown for a hyperspectral cube cross-section at E=1.42 eV. Symmetry conditions were applied for increased SNR (cube flipped around the central axis); the scale is the same as in (b). (b) Measured SPR peak position in the I(E,kx,ky) plane for a given time. The device is in PBS. The dispersion relation of the SP modes for all the emitted energies and wavevectors are thus recorded. Tracking the position of the SPR surfaces in time reveals detailed changes of the surficial conditions. PBS, phosphate-buffered saline; SNR, signal-to-noise ratio; SP, surface plasmon; SPR, surface plasmon resonance.
The presented hyperspectral approach for mapping the QW-SPR emissions offers the advantage of enabling specific studies, such as spectroscopic surficial refractive index changes, through the coupling of broadband SP modes. Concurrently, asymmetries in the SP propagation, due to specific ordering of two-dimensional or three-dimensional surface topologies (such as in photonic crystals), can be monitored using the same measurement cubes. Moreover, the studies of time shifting of the SPR peak for biochemical reactions have shown a larger dynamic range and surface sensitivity, when compared to basic commercial SPR tracking methods. This is because the SPR fluctuations are tracked over E, kx and ky.
However, there are two significant drawbacks to the hyperspectral method for monitoring the SPR signal. The first one concerns the strength of the SPR peak in comparison to the background noise. The resulting signal-to-noise ratio (SNR), defined here by the fraction of extracted SPR flux to the camera noise, is not optimal for biosensing purposes. This is mainly attributed to the low flux coming from the source: where commercial systems employ lasers, here the SP coupling is made through the photoluminescence of a single QW, spread over all angles and a large energy bandwidth. A solution for this, which is currently in development, would be to use an electrically pumped SLED (Superluminescent diode) as an embedded light source that would emit in an even larger emission bandwidth and ample radiant flux. The second drawback is that, while the HI method is relatively fast when taking into account the sheer amount of recorded information, it can be too slow for high-resolution dynamic studies. Indeed, the cubes presented in Figures 6 and 7, of size [2.1 µm−1, 2.1 µm−1, 0.3 eV] and resolution of [3.9×10−3 µm−1, 3.9×10−3 µm−1, 3.2×10−3 eV], are measured in 360 s. Higher resolutions are even more time consuming. A good fraction of the time lag is induced by the camera integration time (1 s per hyperspectral slice) required to capture a significant signal from the low power QW emissions. The other fraction of the time lag is due to the HI working principle, where the system's internal volume Bragg grating (VBG) configuration is modified in time to resolve the full spectral and spatial/wavevector range.16 While this might be acceptable for single measurements or slow biochemical reactions, a finer time resolution would be beneficial for many experiments involving faster reaction times. The presented system is a powerful research tool to study the monolithic QW-SPR platform, which offers broadband and uncollimated emissions. Still, in the end, the multipurpose instrument presented in Figure 5 is bulky in size for simple SPR tracking. Downscaling the whole system into a simplified and portable version remains a requirement for delocalization of applications involving semiconductor SPR platforms.
Conic hyperspectral sections
An initial solution having the potential to resolve the drawbacks of time and system complexity, presents itself when examining more carefully the inner functioning of the HI-conjugate mapping acquisition of SPR. As mentioned previously, during a hyperspectral I(E,k) measurement, a series of images are acquired in time (e.g.: 360 s), as the VBG configuration changes in order to cover all the E and k components. However, for any given position of the VBG, the real-time projection on the camera is actually a tilted cross-section of the scattered light's dispersion relation. Figure 5b illustrates what is occurring at a given time. For any system configuration, a specific plane in E(k) is projected onto the camera, which records a pseudo conic section of the SP dispersion for a set VBG configuration. For a complete cube acquisition, the VBG position is modified in time (with a 1 s integration time per position), which has the effect of moving the tilted plane section (projected on the camera) along the  -axis. Note that
-axis. Note that  stays parallel to kx in Figure 5b. When all the E and ky have been scanned by this tilted plane, the collected set of data are normally rectified, as shown in Figure 7. However, it is possible to use the SPR ellipses, formed by this tilted section, directly. While sacrificing the complete mapping of the dispersion relation, the pseudo conic cross-sections of the SP dispersion still provide valuable information on the SP behaviour in E(k), along the generated ellipses.
stays parallel to kx in Figure 5b. When all the E and ky have been scanned by this tilted plane, the collected set of data are normally rectified, as shown in Figure 7. However, it is possible to use the SPR ellipses, formed by this tilted section, directly. While sacrificing the complete mapping of the dispersion relation, the pseudo conic cross-sections of the SP dispersion still provide valuable information on the SP behaviour in E(k), along the generated ellipses.
Figure 8a presents an example of static measurement in this conic mode. The figure illustrates an unrectified cross-section of the SP dispersion relation, as emitted by the same QW-SPR device in the PBS buffer solution. The signal intensity is normalized for every projected E–ky, but the extracted SPR SNR follows the intensity of the emitted PL (Figure 6). Again, due to a finite NA, only a section of the ellipses generated by the scattered SPAu–PBS are visible. The peaks of the SPR in E–ky and kx can thus be extracted to provide a specific section of the full dispersion of Figure 7. Under this quantification method, the differences in peak position in kx as a function of surface refractive index, for various immersion media, can then be made. As an example of how the SPR shift is measured for different substances, Figure 8b presents the difference in SPR versus the E–ky axis, when a 2% bovine serum albumin solution in PBS is injected over the QW-SPR device: the reference, ΔSPR(E–ky) in PBS, is subtracted. In Figure 8b, it is interesting to note the periodic fluctuations in SPR position as a function of the projected E–ky space. It is believed that this phenomena arises from the interactions between the various forward (+) and backward (−) propagating SP modes when the projected grating wavevector kG is modified (function of E and ky), as predicted in the literature.17
Real-time pseudo conic cross-section of the SPs dispersion. (a) Distribution of the luminescence intensity in the conic cross-section in I(kx,E−ky). Conditions are identical to those of Figure 7; the signal is normalized to unity for every E−ky value for clarity; the SNR thus decreases with the PL intensity of Figure 6. The two elliptical sections correspond to a fraction of the SP dispersion, as shown in Figure 5b. (b) SPR shift between the device in PBS versus a 2% bovine serum albumin solution, for various positions in E–ky. The modulations are due to the interactions between the various SP modes through the grating, as predicted in the literature.17 BSA, bovine serum albumin; PBS, phosphate-buffered saline; PL, photoluminescence; SNR, signal-to-noise ratio; SP, surface plasmon; SPR, surface plasmon resonance.
Even if full dispersion mapping cannot be accomplished using this approach, it does allow for a broad SPR inspection over an arbitrary E–ky spectrum, with resolution dependent mainly on the MO: the resolution of Figure 8 being [1.4×10−3 µm−1, 1.3×10−3 µm−1] for the E–ky, kx axes. The greatest advantage of this novel method of scattering characterization, when compared with a full dispersion scan or even a commercial prism method in the case of SPR tracking, is in the acquisition time. While still susceptible to the emission flux of the QW and the camera sensitivity, collection rates down to 1.2 s are achievable this way. This time response could be ameliorated, given that 1 s of light integration time is employed for the QW source and an additional 0.2 s lag comes from data transfer from the camera.
Finally, the hardware specifications and performance of all the presented systems, including a commercial nanoSPR6 Kretschmann–Raether instrument, are compared in Supplementary Table. It should be noted that there is a difference between absolute hardware resolution and experimental sensitivity, as the later depends on many additional factors other than photonics. A complete biochemical dynamic study, including the SNRs and refractive index unit resolutions yielded by the various experimental quantification methods, is detailed in a separate publication.18
Conclusions
The semiconductor-based device was presented here in an effort towards achieving the total integration of the powerful SPR characterization method. Still far from representing a commercial product, it offers a nonspecific platform for the study of integrated SPR with semiconductor technology, from which many conclusions could be drawn.
We have shown that such complexity transfer was possible and manageable through the use of appropriate analytical tools. To do so, a tensorial version of RCWA was developed in order to design and optimize all the potential variables in play for the construction of a QW-SPR device. These calculations enabled the prediction of the scattering distribution of any layered architecture anywhere in space, as a function of all the properties of electromagnetic fields. In such a way, a specific prototype for biochemical trials in PBS was designed, in which the very general case of uncollimated and broadband light emissions are employed to generate a continuum of SP modes over various energies (E) and surface wavevectors (kx−ky).
The problem with the general case of SPs of unconstrained dispersion relation is that the convoluted relationship between E and k makes the SPR tracking difficult to characterize in an efficient way. To resolve this issue, a modified HI system was employed. This allowed us to record cubes of information in the conjugate plane that yielded the intensity distribution I(E,k) of the scattered light under the MO field of view. The HI method allows the complete characterization of any scattering phenomena and we showed how this can be taken advantage of for the case of diffracted SPs.
One of the main tradeoffs of the HI method was its relatively long acquisition time that could be detrimental for monitoring biochemical reactions. This challenge was resolved in part by using a pseudo conic approach to study the SPR dispersion. Using a simplified hyperspectral system, the acquisition of SPR ellipses can be made, which still hold information on the dispersion of SPs in E(k) and produce surficial characterizations in seconds. The sensitivity of this method might not be as high as that provided by full dispersion mapping, but it would be sufficient for a large range of applications.
A robust evaluation of the experimental sensitivities yielded by the various methods presented in this manuscript has been carried out. The relevant biochemical dynamic study, which has been submitted in a different manuscript, evaluates the quality and capabilities of a QW-SPR platform to be employed for biosensing.
It is reasonable to expect that, by monolithically integrating SPR into a system capable of yielding surface-sensitive outputs, the SPR characterization method could be spread beyond its current niche of biosensing applications. Current nanophotonic knowledge combined with available nanofabrication methods should allow the popularization of this novel SPR platform.
References
Schasfoort RB, Tudos AJ . Handbook of surface plasmon resonance. Camridge: Royal Society of Chemistry, 2008.
Kabashin AV, Patskovsky S, Grigorenko AN . Phase and amplitude sensitivities in surface plasmon resonance bio and chemical sensing. Opt Express 2009; 17: 21191–21204.
de Bruijn HE, Kooyman RP, Greve J . Surface plasmon resonance microscopy: improvement of the resolution by rotation of the object. Appl Opt 1993; 32: 2426–2430.
Lepage D, Dubowski JJ . Surface plasmon assisted photoluminescence in GaAs–AlGaAs quantum well microstructures. Appl Phys Lett 2007; 91: 163106.1–3.
Raether H . Surface-plasmons on smooth and rough surfaces and on gratings. Springer Tracts Mod Phys 1988; 111: 1–133.
Lepage D, Jiménez A, Carrier D, Beauvais J, Dubowski JJ . Hyperspectral imaging of diffracted surface plasmons. Opt Express 2010; 18: 27327–27335.
Lepage D, Dubowski JJ, inventors; Socpra Sciences et Génie S.E.C., assignee. Self-referenced integrated biosensor based on surface plasmon resonance mediated luminescence, EPO Patent EP1956364, 2008
Gu Y, Li J, Martin O, Gong Q . Solving surface plasmon resonances and near field in metallic nanostructures: Green's matrix method and its applications. Chin Sci Bull 2010; 55: 2608–2617.
Carrier D, Dubowski JJ . Demonstration of a novel surface plasmon based interferometer with COMSOL. In: Proceedings of the 6th Annual Comsol Conference; 2010 Oct 7–9; Boston, MA, USA. Retrieve on http://www.dubowski.ca/publications, under Peer-reviewed conference proceedings, 2010. Burlington, MA 01803: COMSOL, pp. 1–6. Permanent link: http://www.comsol.com/papers/8948/ (accessed 31 July 2012).
Glytsis EN, Gaylord TK . Rigorous 3-D coupled wave diffraction analysis of multiple superposed gratings in anisotropic media. Appl Opt 1989; 28: 2401–2421.
Li LF . Fourier modal method for crossed anisotropic gratings with arbitrary permittivity and permeability tensors. J Opt A—Pure Appl Opt 2003; 5: 345–355.
Schuster T, Ruoff J, Kerwien N, Rafler S, Osten W . Normal vector method for convergence improvement using the RCWA for crossed gratings. J Opt Soc Am A—Opt Image Sci Vis 2007; 24: 2880–2890.
Jimenez A, Lepage D, Beauvais J, Dubowski JJ . Study of surface morphology and refractive index of dielectric and metallic films used for the fabrication of monolithically integrated surface plasmon resonance biosensing devices. Microelectron Eng 2012; 93: 91–94.
Lepage D, Dubowski JJ . Surface plasmon effects induced by uncollimated emission of semiconductor microstructures. Opt Express 2009; 17: 10411–10418.
Watts RA, Sambles JR, Harris JB . An experimental test of conical diffraction theory. Opt Commun 1997; 135: 189–192.
Photonetc hyperspectral imaging & spectroscopic instruments. Available at: http://www.photonetc.com (accessed 31 July 2012)
Lepage D, Carrier D, Jimenez A, Beauvais J, Dubowski JJ . Plasmonic propagations distances for interferometric surface plasmon resonance biosensing. Nanoscale Res Lett 2011; 6: 388.
Lepage D, Jimenez A, Beauvais J, Dubowski JJ . Real-time detection of influenza A virus using semiconductor nanophotonics. Light: Science & Applications, submitted 5 June 2012.
Acknowledgements
The authors acknowledge the financial contribution from the Natural Sciences and Engineering Research Council of Canada (NSERC Strategic grant STPGP 350501-07), the Canada Research Chair in Quantum Semiconductors Program and the Vanier Scholarship CGS program. The authors also want to thank the CRN2 nanofabrication team for their helpful participation.
Author information
Authors and Affiliations
Additional information
Note: Supplementary informationfor this article can be found on Light: Science & Applications' website .
Supplementary information
Rights and permissions
This work is licensed under the Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Lepage, D., Jiménez, A., Beauvais, J. et al. Conic hyperspectral dispersion mapping applied to semiconductor plasmonics. Light Sci Appl 1, e28 (2012). https://doi.org/10.1038/lsa.2012.28
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2012.28
Keywords
This article is cited by
-
Real-time detection of influenza A virus using semiconductor nanophotonics
Light: Science & Applications (2013)
-
Silver nano islands enhanced Raman scattering on large area grating substrates fabricated by two beam laser interference
Chemical Research in Chinese Universities (2013)