Abstract
Pure lines derived from multiple parents are becoming more important because of the increased genetic diversity, the possibility to conduct replicated phenotyping trials in multiple environments and potentially high mapping resolution of quantitative trait loci (QTL). In this study, we proposed a new mapping method for QTL detection in pure-line populations derived from four-way crosses, which is able to control the background genetic variation through a two-stage mapping strategy. First, orthogonal variables were created for each marker and used in an inclusive linear model, so as to completely absorb the genetic variation in the mapping population. Second, inclusive composite interval mapping approach was implemented for one-dimensional scanning, during which the inclusive linear model was employed to control the background variation. Simulation studies using different genetic models demonstrated that the new method is efficient when considering high detection power, low false discovery rate and high accuracy in estimating quantitative trait loci locations and effects. For illustration, the proposed method was applied in a reported wheat four-way recombinant inbred line population.
Similar content being viewed by others
Introduction
Pure-line development is a major task in plant breeding for both self-pollinated and cross-pollinated species. Populations consisting of pure lines can be planted repeatedly in multiple years and locations so as to improve the detection power of quantitative trait loci (QTL) and conduct QTL by environment interaction analysis. Many genetic researches have been conducted on biparental pure lines (such as doubled haploids (DH) and recombinant inbred lines), where only two alleles are involved per locus, opportunities for genetic cross-over and recombination are limited and QTL mapping resolution is low (Holland, 2007). To save time in population development and identify more alleles at one locus, association mapping has been employed for genetic studies with natural populations in many species of plants. It relies on population-wide marker-phenotype associations and historical recombination events, and may suffer from issues caused by unknown population substructure and cryptic relatedness, thereby distorting the relationship between markers and traits (Verbyla et al., 2014a). As a result, association mapping in plants has so far failed to identify a single major QTL allele that has been of value in public breeding programs (Bernardo, 2016).
Multiparental pure-line populations are becoming important in genetic studies. Each locus may contain multiple alleles in multiparental populations. Kinship in the progenies is clear; therefore, population structure issue does not exist. Greater opportunities for recombination increase the mapping accuracy, and the abundant genetic variation allows the detection of more genes and alleles (Kover et al., 2009). Multiparent advanced generation inter-cross (MAGIC) populations in crop was first advocated by Cavanagh et al. (2008), and the designs have been applied in a number of species. Bandillo et al. (2013) developed four MAGIC populations in rice, and genome-wide association mapping was used for QTL identification. Würschum et al. (2014) performed QTL mapping by genome-wide association mapping in a six-parental DHs triticale population. Mackay et al. (2014) created a set of eight-parental recombinant inbred lines (RIL) of winter wheat and identified a diagnostic marker for morphological character ‘awn presence/absence’ by association mapping. Sannemann et al. (2015) incorporated multilocus QTL analysis and cross-validation for flowering time in the first eight-way MAGIC DH population of barley.
For QTL detection in multiparental populations, software packages R/HAPPY (Mott et al., 2000), R/qtl (Broman et al., 2003), MCQTL (Jourjon et al., 2005) and R/mpMap (Huang and George, 2011) have implemented interval mapping (IM; Lander and Botstein, 1989) and composite interval mapping (CIM; Zeng, 1994). IM and CIM were first proposed in biparental populations and then extended to multiparental populations. Under the assumption that there was at most one QTL located in each chromosome, IM calculated likelihood of odd (LOD) scores at scanning positions, and QTL were supposed to be located at the LOD profile peaks above a threshold value (Lander and Botstein, 1989). Estimates of QTL positions and effects were biased when QTL were linked. CIM combines IM with marker regression to control the QTL effects outside the scanning interval (Zeng, 1994). But the arbitrariness of cofactor selection complicated the application of CIM (Li et al., 2007; Wang et al., 2016; Wei and Xu, 2016). Verbyla et al. (2014a) proposed the whole-genome average interval mapping method for multiparental populations (MPWGAIM). Wei and Xu (2016) showed that MPWGAIM was time-consuming if the number of markers and QTL were large, and presented four mixed models for QTL mapping. Two models called FIXED-B and RANDOM-B were proven by the authors to have higher powers and lower false discovery rate (FDR) than MPWGAIM.
Background control algorithm of QTL mapping was first proposed by Zeng (1993) and Jansen (1993). In previous studies, inclusive CIM (ICIM) has been developed for additive, dominance and epistatic mapping in biparental populations (Li et al., 2007, 2008; Zhang et al., 2008, 2012; Wang, 2009), and then extended to clonal F1 and four-way cross F1 populations (Zhang et al., 2015). The background control algorithm used in ICIM results in sharp and clear peaks around the QTL locations, which helps the separation of linked QTL. QTL mapping methodology is less investigated in multiparental pure-line populations compared with biparental populations. In this study, we developed an ICIM-based new QTL mapping method for pure-line populations derived from four-way crosses, compared our method with others by simulation studies and demonstrated its efficiency in one wheat four-way RIL population.
Materials and methods
Two single crosses are first made from four homozygous inbred parents. Four-way cross F1 population is then generated from the two single crosses. Finally, pure lines consisting of DHs can be produced by pollen culture technology, or RILs produced by repeated selfing (Figure 1).
Linear regression model in pure-line populations of four-way crosses
Assume Aq, Bq, Cq and Dq were the four alleles at one QTL. Genotypic value of an individual with known QTL genotype was written in the one-locus model, that is, Equation (1), where μ was the mean of the four homozygous QTL genotypes; μk (k=1, 2, 3, 4) was the kth genotypic value of QTL; ak (k=1, 2, 3, 4) was the kth genotypic effect and wk (k=1, 2, 3, 4) was the indicator of QTL genotype valued at 1 for the kth genotype, and 0 for the other genotypes.

From Equation (1), mean and the four genotypic effects were calculated and shown in equation (2).

When there was no segregation distortion, the genetic variance contributed by the QTL was given in Equation (3).

One restriction has to be made so as to estimate the five genetic parameters (that is, μ, a1, a2, a3 and a4) in Equation (1), that is, sum of the four genotypic effects was equal to 0. To avoid the complexity caused by the restricted condition in parameter estimation, one orthogonal model equivalent to Equation (1) but without restriction was built in Equation (4), where d1= (a1+a2)/2, d2= (a1+a3)/2, d3= (a1+a4)/2; u and v were the orthogonal indicators of QTL genotypes valued at 1 and 1 for AqAq, 1 and −1 for BqBq, −1 and 1 for CqCq and −1 and −1 for DqDq. Letting X represent the 4 × 4 design matrix in Equation (4), it can be easily seen that XTX is a diagonal matrix, indicating its orthogonality.

Assume that A1, B1, C1 and D1 were the four alleles at the left-flanking marker of the QTL, and A2, B2, C2 and D2 were the four alleles at the right-flanking marker of the QTL. One-meiosis recombination frequency and accumulated recombination frequency during the repeated selfing generations were denoted as r and R, respectively, where the relationship between them was  (Haldane and Waddington, 1931). In total, there were 16 identifiable marker classes (Table 1 for DH population and Table S1 for RIL population). For each marker locus, two indicators were defined and denoted by x and y, respectively, similar to indicators u and v of QTL genotypes. In Equation (4), x1 and y1 were the indicators for the left marker, valued at 1 and 1 for marker type A1A1, 1 and −1 for B1B1, −1 and 1 for C1C1 and −1 and −1 for D1D1; x2 and y2 were the indicators for the right marker, valued at 1 and 1 for marker type A2A2, 1 and −1 for B2B2, −1 and 1 for C2C2 and −1 and −1 for D2D2. Similar to QTL effects in Equation (4), left marker effects were denoted by D1L, D2L and D3L, and right marker effects were denoted by D1R, D2R and D3R. Interaction effects between the two markers were denoted by DDij, i, j=1, 2 and 3, where i represented the left marker and j represented the right marker. Relationship between marker class means and marker effects was shown in Equation (5), where μM was the mean of the 16 marker classes.
(Haldane and Waddington, 1931). In total, there were 16 identifiable marker classes (Table 1 for DH population and Table S1 for RIL population). For each marker locus, two indicators were defined and denoted by x and y, respectively, similar to indicators u and v of QTL genotypes. In Equation (4), x1 and y1 were the indicators for the left marker, valued at 1 and 1 for marker type A1A1, 1 and −1 for B1B1, −1 and 1 for C1C1 and −1 and −1 for D1D1; x2 and y2 were the indicators for the right marker, valued at 1 and 1 for marker type A2A2, 1 and −1 for B2B2, −1 and 1 for C2C2 and −1 and −1 for D2D2. Similar to QTL effects in Equation (4), left marker effects were denoted by D1L, D2L and D3L, and right marker effects were denoted by D1R, D2R and D3R. Interaction effects between the two markers were denoted by DDij, i, j=1, 2 and 3, where i represented the left marker and j represented the right marker. Relationship between marker class means and marker effects was shown in Equation (5), where μM was the mean of the 16 marker classes.

Based on the expected frequencies of QTL genotypes in each marker class (Table 1 and Supplementary Table S1), expectations of QTL indicators and mean performance of each marker class can be calculated and shown in Supplementary Table S2 for DH population and Supplementary Table S3 for RIL population. From Equation (5) and Supplementary Tables S2 and S3, the relationship between marker effects and QTL effects was derived and given in Equation (6) for DH population and Equation (7) for RIL population.

where  ,
,  ,
,  ,
,  ,
,  ,
,  , and f1, f2, …, and f6 were functions of recombination frequencies defined in Supplementary Table S2.
, and f1, f2, …, and f6 were functions of recombination frequencies defined in Supplementary Table S2.

where  ,
,  ,
,  ,
,  ,
,  ,
,  , and g1, g2, …, and g5 were functions of recombination frequencies defined in Supplementary Table S3.
, and g1, g2, …, and g5 were functions of recombination frequencies defined in Supplementary Table S3.
From Equations (6) and (7), if there was one QTL between two flanking markers, the QTL effects caused both main effects and interactions of markers. This phenomenon was similar to that reported in biparental F2 populations (Zhang et al., 2008). However, coefficients of marker interactions were much smaller than those of marker main effects; that is, F5 and F6 were much smaller than F1 to F4, and G5 and G6 were much smaller than G1 to G4. For example, when the recombination frequencies between the left marker and QTL, and between QTL and the right marker, that is, r1 and r2, were 0.1 and 0.15, F1 to F4 were equal to 0.37, 0.54, 0.59 and 0.32, but F5 and F6 were equal to 0.04 and 0.05; G1 to G4 were equal to 0.53, 0.52, 0.33 and 0.32, but G5 and G6 were equal to 0.04 and 0.02. From Equations (6) and (7), it can be seen that marker interaction effects were also much smaller than marker main effects. Most variations of the QTL could be absorbed by main effects of neighboring markers, and therefore marker interactions were ignored in this study.
For simplicity, we assumed m QTL were located at m intervals defined by m+1 markers. Genotypic value of an individual in one DH or RIL population derived from four-way cross was defined in Equation (8).

where uj and vj were indicators for genotypes at the jth QTL, having the same meaning as given in Equation (4). The inclusive linear model containing all markers simultaneously was given in Equation (9).

where P was the phenotypic value of the trait of interest; ɛ was the random error assumed to be normally distributed and αj, βj and τj were the effects of the jth marker. For large-size populations, it can be shown that the coefficients of individual markers in Equation (9) were only affected by the QTL located at their left and right intervals. In other words, six variables of the two closest markers could almost completely absorb the QTL effects. The linear model defined by Equation (9) explained the effects of all QTL, and therefore it can be used to control background genetic variation in QTL mapping.
Background-controlled one-dimensional scanning
Similar to biparental and four-way cross F1 populations (Li et al., 2007; Zhang et al., 2008, 2015), a two-stage strategy was considered in QTL mapping. First, significant marker variables in Equation (9) were selected only once by stepwise regression. Coefficients of those variables not retained by stepwise regression were set at 0. Second, during the one-dimensional scanning, the phenotypic values were adjusted and subsequently used in interval mapping, that is, Equation (10).

where t and t+1 represented the two flanking markers of the current scanning position, i ( ) representing ith line in the population and the hat symbol meant ‘estimated’. The adjusted phenotypic value
) representing ith line in the population and the hat symbol meant ‘estimated’. The adjusted phenotypic value  contained QTL information of the current interval and did not change until the testing position moved to the next interval. At a testing position in interval [t, t+1], phenotypes of individuals having the four QTL genotypes followed normal distributions, that is,
contained QTL information of the current interval and did not change until the testing position moved to the next interval. At a testing position in interval [t, t+1], phenotypes of individuals having the four QTL genotypes followed normal distributions, that is,  , k=1, 2, 3 and 4. Existence of QTL at the current scanning position was tested by the following hypotheses:
, k=1, 2, 3 and 4. Existence of QTL at the current scanning position was tested by the following hypotheses:
H0: μ1=μ2=μ3=μ4 vs
HA: at least two of μ1, μ2, μ3 and μ4 were not equal.
The log-likelihood function under the alternative hypothesis HA was

where Sj denoted individuals belonging to the jth marker class (j=1, 2, …, 16); πjk (k=1, 2, 3, 4) was the proportion of the kth QTL genotype in the jth marker class (Table 1 and Supplementary Table S1) and  represented the density function of normal distribution
represented the density function of normal distribution  .
.
EM algorithm (Dempster et al., 1977) was used for maximum likelihood estimation in Equation (11). Most individuals in marker classes 1, 6, 11 and 16 had QTL genotypes AqAq, BqBq, CqCq and DqDq, respectively. Hence, the initial values of parameters used in the EM algorithm were defined as follows, where ni:j represented the summation from ni to nj.

In the E-step, posterior probability of the ith individual belonging to the kth QTL genotype was calculated by the following equation, where i∈Sj.

In the M-step, parameters in the log-likelihood function were updated by,

Under the null hypothesis, the four QTL genotypes followed the same normal distribution, denoted by  . Parameters under H0 were calculated as follows:
. Parameters under H0 were calculated as follows:

LOD score between HA and H0 was calculated from the maximum likelihoods under the two hypotheses. To better understand the equations above, Supplementary Table S4 showed the definition of parameters used in this study.
QTL models in simulation
RIL populations of four-way crosses were simulated for power analysis and comparison with other methods to illustrate the efficiency of ICIM. The simulated genome consisted of five chromosomes, each of which was 110 cM in length with 12 evenly distributed markers. One independent and two linkage genetic models were considered. In model I, four independent QTL with different effects were located on the first four chromosomes (Table 2). The four QTL were represented by Q1–Q4, whose genetic variances were 2.5, 5, 7.5 and 10, respectively. Total genetic variance from the four QTL was equal to 25. The random error variance was set at 30.5, resulting in a broad-sense heritability at 0.45.
Models II and III both had two QTL (that is, Q1 and Q2), located at 25 and 55 cM on chromosome 1 (Table 2) with genetic variances at 5 and 10, respectively. Q1 and Q2 were linked in repulsion phase in model II, effects of which were set at opposite directions. Q1 and Q2 were linked in coupling phase in model III, effects of which were set at same directions (Table 2). Calculated from theoretical genotypic frequencies in Table 1 and Supplementary Table S1, total genetic variances explained by the two QTL were 5.93 and 24.14 in models II and III, respectively. For better comparison between the two linkage models, random error variance was set equally at 18.5, resulting in heritability values at 0.24 and 0.57 for the two models, respectively (Table 2).
Two population sizes were considered, that is, 200 and 500. For each genetic model and each population size, one thousand simulated populations were generated by the genetics and breeding simulation tool of QuLine (Wang et al., 2003). IM and ICIM were implemented in the GAPL software, an integrated tool for linkage map construction and QTL mapping in multiparental pure-line populations (freely available from http://www.isbreeding.net). Two probabilities of entering and removing variables for the stepwise regression in ICIM were set at 0.001 and 0.002, respectively. For comparison, QTL mapping by CIM was conducted in the R/mpMap package (Huang and George, 2011). The method used for selecting cofactors in CIM was backward selection with P-value at 0.001, and the number of cofactors retained in the model was set at 10 for background control. QTL mapping by FIXED-B and RANDOM-B methods was conducted in the MagicQTL package (Wei and Xu, 2016).
Additional one thousand populations with a size of 200 were simulated for the null QTL model to estimate the empirical distribution of the test statistics for different mapping methods, that is, LOD score for ICIM and IM, and LOGP score (namely –log10(P)) for the other methods. The largest LOD (or LOGP) score in each simulated population was recorded, and the 95% quantile of the largest LOD (or LOGP) scores was adopted as the threshold value to control type I error under 0.05 across the whole genome.
Detection power and FDR were computed and then used to compare different mapping methods. Each predefined QTL was assigned to a support interval of 10 cM centered at the true QTL location. Power of each QTL was the proportion of simulation runs where significant peaks were higher than the threshold in the support interval. QTL identified out of the support interval were treated as false positives, and FDR was defined as a proportion of false positives to the total number of significant discoveries (that is, true positives plus false positives, Li et al., 2010). Positions and effects at the significant peaks in the support interval were used for calculating their averages.
One actual RIL population in wheat
As an example, the actual population used in this study was derived from four Australian wheat cultivars (Yitpi, Baxer, Chara and Westonia; Huang et al., 2012). A total of 1063 pure lines were generated by single seed descent, and sequenced with SNPs, DArTs and microsatellites. 1000-kernel weight (TKW) was evaluated in field at Yanco, New South Wales in 2009. The broad-sense heritability of TKW in the population was estimated at 0.85 (Verbyla et al., 2014b). The linkage map constructed by Verbyla et al. (2014a) was used in QTL mapping.
Results
Thresholds of different mapping methods
Distributions of the test statistics in different methods were obtained by running these methods on simulated populations from the null QTL model, by which the thresholds were determined to control the genome-wide type I error at an equal level of 0.05. The threshold LOD score thus obtained was 3.776 for ICIM and IM. The threshold LOGP values were 5.498 for CIM, 3.111 for FIXED-B method and 2.521 for RANDOM-B method.
In the actual population, the LOD threshold was set at 5.00 for ICIM, which was derived from the empirical formula under the genome-wide type I error at 0.05 (Sun et al., 2013). For comparison with results from Verbyla et al. (2014b) where LOGP was used as the test statistic, LRT was calculated from LOD score (LRT=2ln(10)LOD≈4.61 × LOD) and then a P-value was obtained from the χ2 distribution with df=3. Consequently, the LOGP threshold was set at 4.399. In other words, LOD threshold at 5.00 and LOGP threshold at 4.399 both can control the genome-wide type I error under 0.05.
Power analysis and mapping results in simulated populations of size 200
Detection powers and FDR for population size 200 were shown in Table 3 for the three simulated models and five mapping methods. In unlinked model I, ICIM had substantially higher power and lower FDR than CIM, FIXED-B and RANDOM-B. Taking Q1 as an example, detection powers were 20.0, 8.7, 3.2 and 3.0% from ICIM, CIM, FIXED-B and RANDOM-B, respectively; and the respective FDR were 27.43, 33.45, 34.02 and 33.81% (Table 3). Compared with IM, ICIM had higher powers for two smallest QTL, but slightly lower powers for two largest QTL. Q1 was one of the smallest, and Q3 was one of the largest. Their detection powers were 20.0 and 78.0% from ICIM and 13.9 and 79.8% from IM. When summing up powers of all the four QTL in model I, ICIM had higher powers than IM. Both methods had similar FDR (Table 3).
In linked model II of repulsion phase, ICIM achieved much higher power for the smaller QTL (that is, Q1), similar power for the larger QTL (that is, Q2) and similar FDR compared with IM. Compared with CIM, ICIM achieved similar powers for both QTL and much lower FDR. Compared with FIXED-B and RANDOM-B, ICIM achieved much higher power for Q1, similar power for Q2 and much lower FDR (Table 3).
In linked model III of coupling phase, detection powers from ICIM were similar or lower than those from IM, FIXED-B and RANDOM-B. However, FDR from ICIM was much lower. For example, powers of Q2 were 97.6, 98.7, 90.1, 99.0 and 99.0% from ICIM, IM, FIXED-B and RANDOM-B, respectively. FDR from ICIM was 25.23%. FDR from IM, FIXED-B and RANDOM-B were 48.83, 54.51 and 54.41%, respectively (Table 3), approximately twice of that from ICIM. CIM had lower power and higher FDR than ICIM. For instance, powers of Q1 and Q2 were 79.9 and 97.6% from ICIM, respectively, but 53.3 and 90.1% from CIM. FDR from CIM was 36.93%, 11.70% higher than that from ICIM (Table 3). Considering its higher detection power and lower FDR compared with other methods, we conclude that ICIM is an efficient mapping method.
For all mapping methods, detection powers were lower in repulsion linkage model II than those in coupling linkage model III. Absolute values of QTL effects were the same for the two models. Due to different linkage phases, total genetic variance in model II was much lower than that in model III (Table 2). As the error variance was the same, heritability of model II was also much lower than that in model III. Higher genetic variance and heritability is the reason for the higher detection power for coupling linkage.
QTL positions and effects estimated by ICIM, IM, FIXED-B and RANDOM-B for population size 200 were shown in Supplementary Figure S1. For estimates of QTL positions, ICIM achieved the smallest biasness at 5 out of the 8 positions in the three models, IM achieved at 3, FIXED-B and RANDOM-B achieved at 0. The average biasness was 0.34, 0.69, 0.58 and 0.55 for the four methods, respectively. For estimates of QTL effects, ICIM achieved the smallest biasness at 19 out of the 32 effects in the three models, IM achieved at 4, FIXED-B achieved at 5 and RANDOM-B achieved at 4. The average biasness was 0.28, 0.61, 0.65 and 0.43 for the four methods, respectively. Obviously, ICIM gave the most accurate estimates of QTL positions and effects.
Power analysis and mapping results in simulated populations of size 500
Detection powers and FDR for population size 500 were shown in Table 4. In all the three models, ICIM had either similar or higher powers for each QTL, and substantially lower FDR than the other four mapping methods. Except Q1 in model I, powers from ICIM were close to 100%. Compared with population size 200 (Table 3), detection powers of all QTL were increased from all mapping methods in all models. FDR from all methods were decreased as the increase in population size in model I. So were FDR from ICIM, CIM, FIXED-B and RANDOM-B in models II and III. However, FDR from IM were even larger for population size 500 in models II and III.
QTL positions and effects estimated by ICIM, IM, FIXED-B and RANDOM-B for population size 500 were shown in Supplementary Figure S2. For estimates of QTL positions, ICIM achieved the smallest biasness at 5 out of the 8 positions in the three models, IM achieved at 2, FIXED-B achieved at 1 and RANDOM-B achieved at 0. The average biasness was 0.22, 0.76, 0.40 and 0.40 for the four methods, respectively. For estimates of QTL effects, ICIM achieved the smallest biasness at 14 out of the 32 effects in the three models, IM achieved at 11, FIXED-B achieved at 4 and RANDOM-B achieved at 3. The average biasness was 0.16, 0.51, 0.42 and 0.24 for the four methods, respectively. Once again, ICIM provided the most accurate estimates of QTL positions and effects. Compared with population size 200, deviations of QTL positions and effects from ICIM, FIXED-B and RANDOM-B were decreased as the increase in population size. Deviations of QTL effects from IM were also decreased, but deviations of QTL positions from IM were similar when the three models were considered together.
QTL for TKW identified in the actual wheat population
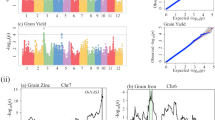
Profile of LOD score from ICIM in the actual wheat population was shown in Figure 2, using TKW as the phenotypic trait. Profiles of estimated effects were shown in Supplementary Figure S3. Under LOD threshold of 5.00, a total of eight QTL were identified by ICIM, one each on chromosomes 2 A and 7 A, four on chromosome 2B and two on chromosome 2D (Table 5). Seven of them were located on homologous chromosome group 2, where a large number of yield-related QTL have been reported by Zhang et al. (2010). PVE by each QTL varied from 1.83 to 4.44%. qTKW2B-4 had the largest LOD score (that is, 12.50) and explained the highest PVE (that is, 4.44%). qTKW2D-1 had a LOD score at 9.40 and PVE at 3.39%, which was the second largest by LOD and PVE. Its confidence interval was estimated from 27.5 to 38.5 cM. In this region, Williams and Sorrells (2014) have reported a QTL affecting TKW, and the QTL position was near gene Ppd-D1 located around 34 cM on chromosome 2D and involved in photoperiod insensitivity to long days.
Under LOGP threshold of 4.399, MPWGAIM detected three QTL, two on chromosome 2B and one on chromosome 2D (Table 5, adapted from Supplementary Table S2 in Verbyla et al. (2014b)). q2B-2 had the largest LOGP of 5.63 and was located on chromosome 2B. When a confidence interval at 10 cM was considered, qTKW2B-2 and qTKW2D-2 from ICIM were overlapped with q2B-1 and q2D from MPWGAIM, respectively (Table 5). For the two common QTL, estimated effects from the two methods were at the same directions (Table 5). ICIM gave similar LOD score with MPWGAIM for one common QTL (that is, qTKW2D-2 and q2B-1), but significant higher LOD score for the other one (that is, qTKW2B-2 and q2D). LOD score is the statistic indicating the existence of QTL. Due to the efficient background control, ICIM resulted in high LOD score and sharp peaks around QTL positions. Higher LOD score helped QTL detection, and sharper peaks helped separate genetic linkage, which explained the larger number of QTL detected by ICIM in the actual population.
Kernel weight has high heritability, which has been efficiently improved by conventional phenotypic selection in wheat breeding. It is understandable that a significant amount of genotypic variation on TKW is due to additive effects. Under the same significance level at 0.05, ICIM detected more QTL than MPWGAIM (Table 5). Total PVE was 20.75% for the eight QTL from ICIM. Total genotypic variation explained was 15.6% for the three QTL from MPWGAIM (Verbyla et al., 2014b). PVE is the proportion of genetic variance caused by one QTL to the whole phenotypic variance, whereas genotypic variation explained is the proportion to the genotypic variance. If given, total PVE of the three QTL from MPWGAIM should be smaller than 15.6% and thus smaller than the total PVE from ICIM. More QTL identified by ICIM explained larger PVE, better illustrating the genetic architecture of TKW.
Discussion
Handling of incomplete and missing markers
In the four parental lines, some markers may have four identifiable alleles, but others may have fewer. Based on the number of identifiable alleles in parents, 14 marker categories were defined and denoted as ABCD, AACD, ABCC, ABAD, ABCA, ABBD, ABCB, AACC, ABAB, ABBA, ABBB, ABAA, AACA and AAAD. For markers belonging to category ABCD (also called complete markers), parents had four identifiable alleles, denoted by A, B, C and D. In their DHs or RILs, four distinctive genotypes were represented by AA, BB, CC and DD, following the Mendelian ratio of 1:1:1:1 when no distortion occurred. Markers belonging to the other 13 categories cannot completely distinguish the four alleles in parents, which were called incomplete markers. For example, if alleles A and B were not identifiable, the corresponding genotypes were denoted as AA+BB, and the marker category was denoted as AACD. When no distortion occurred, the three genotypes AA+BB, CC and DD followed the Mendelian ratio of 2:1:1.
After linkage map construction, incomplete markers and missing marker types were imputed for QTL mapping by conditional probabilities calculated from genotypic frequencies in Table 1 or Supplementary Table S1. For example, for markers belonging to category AACD, genotype AA+BB was imputed to either AA or BB. For markers belonging to category AAAD, genotype AA+BB+CC was imputed to either AA, BB or CC. Completely missing genotype was imputed into either AA, BB, CC or DD. After imputation, all markers belonged to category ABCD. Therefore, in this study, all markers were assumed to have four identifiable alleles and there were no missing marker types.
Advantages of ICIM compared with other methods
ICIM was first proposed for QTL mapping in biparental populations and has been widely applied in QTL mapping researches, for example, in wheat (Zhu et al., 2016), soybean (Li et al. (2016)), maize (Mahuku et al. (2016)) and rice (Fiyaz et al. (2016)). ICIM has been extended to Nested Association Mapping (NAM) populations (Li et al., 2011) and clonal F1 and four-way cross F1 populations (Zhang et al., 2015). Extensive simulations showed that ICIM is an efficient mapping method with higher detection power, lower FDR and less-biased estimation of QTL effects and positions in these populations (Li et al., 2007, 2008; Zhang et al., 2008, 2015; Wang, 2009).
In this study, orthogonal variables were defined for each marker in an inclusive regression model to build the relationship between phenotype and markers. Phenotype was adjusted by estimated regression model and then used in interval mapping. The design matrix X in Equation (4) was similar to the design matrix H in Xu (1998) for four-way cross population, where HTH was a diagonal matrix, but the absolute values of elements from the last column of H were twice of those from the first two columns. The diagonal elements of XTX were equal, but the diagonal elements of HTH were not equal.
Obviously, one mapping method is more powerful for detecting QTL with relatively larger effects. However, considering that major QTL may have been fixed after many years of selection, small-effect genes may be more important for future breeding. Meanwhile, multiple genes contribute together to one complex trait. Therefore, linkage becomes a common phenomenon, but closely linked QTL are still difficult to separate. For two QTL linked in the coupling phase, one ghost QTL may be declared in the middle of the two QTL positions. While for QTL linked in the repulsion phase, neither of them may be detected. Five mapping methods were compared in this study, that is, IM, CIM, FIXED-B, RANDOM-B and ICIM. IM behaved the worst in detecting small-effect QTL, especially when two QTL were linked in repulsion. Wei and Xu (2016) showed that CIM behaved poorly when the number of cofactor markers were larger than 10 and then proposed the FIXED-B and RANDOM-B methods. However, neither method had sufficient power to detect small-effect QTL (Wei and Xu, 2016). Similar results were observed in this study. Simulations based on various genetic models and the application in one actual wheat population demonstrated that most advantages of ICIM were maintained when extended to QTL mapping in four-way cross pure-line populations. Compared with other methods, ICIM had higher power for detecting small-effect QTL, less-biased estimation of QTL locations and effects and better separation of linked QTL.
Strength and weakness of four-way cross pure-line populations in QTL mapping
One major advantage of four-way cross pure-line populations is to detect QTL with multiple alleles. Taking Q2 in simulated model II for example, a1 and a2 had the same value at 1.1, indicating equal genotypic values of the first two parents at the QTL position. In the biparental population derived from the first two parents (not considering dominance effect), Q2 cannot be detected. But in four-way cross pure-line populations, it will be detected because of the unequal effects of the other two alleles.
For QTL having same PVE, detection power may be lower in four-way cross pure-line populations than that in biparental populations due to the increased number of genetic effects and degree of freedom of the test statistic. There were two classes at each marker locus in biparental pure-line populations, but four classes in four-way cross pure-line populations. Assuming that the population size was fixed, the sample size of each marker class was smaller in four-way cross pure-line populations. Therefore, it is understandable that QTL detection power in four-way cross pure-line populations may be lower. A larger size is needed to achieve similar power.
In biparental pure-line populations, only one variable was needed for each marker. In biparental F2 or F3 populations, two orthogonal variables were needed. However, in four-way cross pure-line populations, three orthogonal variables were needed for each marker. Obviously, more variables were included in the linear regression model (Equation (9)), and overfitting problem may be more serious. The overfitting problem can be reduced by choosing a smaller probability of variables entering the model in stepwise regression.
Wider applications of the proposed mapping method
In a four-way cross represented by (A × B) × (C × D), if parent C is the same as A, and D is the same as B, it is equivalent to a biparental F2 population of single cross A × B. Thus, a biparental pure-line population can be treated as a special case of four-way cross, where all markers belong to category ABAB. If D is the same as C, the four-way cross is equivalent to top cross (A × B) × C, where all markers belong to category ABCC. If D is the same as A, the four-way cross only has three parents, where all markers belong to category ABCA. Therefore, the QTL mapping method proposed in this study can be directly used for pure-line populations derived from biparental F2, three-way cross F1 and three-parental four-way cross F1.
To use multienvironmental phenotyping trials in genetic studies of quantitative traits, ICIM has been extended as well for QTL by environment interaction analysis in biparental populations (Li et al., 2015). Pure lines derived from multiple parents allow multienvironment replicated trials. There is a need for QTL by environment interaction analysis for such populations. Epistasis is an important source of variation for complex traits, which could maintain additive variance and assure the long-term genetic gain in breeding (Zhang et al., 2012). To our knowledge, epistatic mapping method in multiparental populations has not been studied yet. ICIM has been applied for mapping epistatic QTL in biparental populations (for example, Lu et al., 2009; Alves et al., 2012). We are considering epistatic QTL mapping for multiparental pure-line populations. In addition, we are also considering mapping methods for pure lines derived from more parental lines. Once developed, the corresponding methods will be implemented in our software package GAPL.
Data archiving
The ICIM-based new method of QTL mapping for pure-line populations derived from four-way crosses was implemented in software package GAPL, which is freely available from the website http://www.isbreeding.net. All data including simulation study and the actual wheat four-way RIL population are downloadable from the website http://www.isbreeding.net/GAPL.
References
Alves AA, Rosado CCG, Faria DA, Guimarães LMS, Lau D, Brommonschenkel SH et al. (2012). Genetic mapping provides evidence for the role of additive and non-additive QTLs in the response of inter-specific hybrids of Eucalyptus to Puccinia psidii rust infection. Euphytica 183: 27–38.
Bandillo N, Raghavan C, Muyco PA, Sevilla MAL, Lobina IT, Dilla-Ermita CH et al. (2013). Multi-parent advanced generation inter-cross (MAGIC) populations in rice: progress and potential for genetics research and breeding. Rice 6: 11.
Bernardo R . (2016). Bandwagons I, too, have known. Theor Appl Genet 129: 2323–2332.
Broman KW, Wu H, Sen S, Churchill GA . (2003). R/qtl: QTL mapping in experimental crosses. Bioinformatics 19: 889–890.
Cavanagh C, Morell M, Mackay I, Powell W . (2008). From mutations to MAGIC: resources for gene discovery, validation and delivery in crop plants. Curr Opin Plant Biol 11: 215–221.
Dempster AP, Laird NM, Rubin DB . (1977). Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B 39: 1–38.
Fiyaz RA, Yadav AK, Krishnan SG, Ellur RK, Bashyal BM, Grover N et al. (2016). Mapping quantitative trait loci responsible for resistance to Bakanae disease in rice. Rice 9: 45.
Haldane JBS, Waddington CH . (1931). Inbreeding and linkage. Genetics 16: 357.
Holland JB . (2007). Genetic architecture of complex traits in plants. Curr Opin Plant Biol 10: 156–161.
Huang BE, George AW . (2011). R/mpMap: a computational platform for the genetic analysis of multi-parent recombinant inbred lines. Bioinformatics 27: 727–729.
Huang BE, George AW, Forrest KL, Kilian A, Hayden MJ, Morell MK et al. (2012). A multiparent advanced generation inter-cross population for genetic analysis in wheat. Plant Biotechnol J 10: 826–839.
Jansen RC . (1993). Interval mapping of multiple quantitative trait loci. Genetics 135: 205–211.
Jourjon MF, Jasson S, Marcel J, Ngom B, Mangin B . (2005). MCQTL: multi-allelic QTL mapping in multi-cross design. Bioinformatics 21: 128–130.
Kover PX, Valdar W, Trakalo J, Scarcelli N, Ehrenreich IM, Purugganan MD et al. (2009). A multiparent advanced generation inter-cross to fine-map quantitative traits in Arabidopsis thaliana. PLOS Genet 5: e1000551.
Lander ES, Botstein D . (1989). Mapping mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121: 185–199.
Li H, Ye G, Wang J . (2007). A modified algorithm for the improvement of composite interval mapping. Genetics 175: 361–374.
Li H, Ribaut JM, Li Z, Wang J . (2008). Inclusive composite interval mapping (ICIM) for digenic epistasis of quantitative traits in bi-parental populations. Theor Appl Genet 116: 243–260.
Li H, Hearne S, Bänziger M, Li Z, Wang J . (2010). Statistical properties of QTL linkage mapping in biparental genetic populations. Heredity 105: 257–267.
Li H, Bradbury P, Ersoz E, Buckler ES, Wang J . (2011). Joint QTL linkage mapping for multiple-cross mating design sharing one common parent. PLoS ONE 6: e17573.
Li S, Wang J, Zhang L . (2015). Inclusive composite interval mapping of QTL by environment interactions in biparental populations. PLoS One 10: e0132414.
Li H, Yang Y, Zhang H, Chu S, Zhang X, Yin D et al. (2016). A genetic relationship between phosphorus efficiency and photosynthetic traits in soybean as revealed by QTL analysis using a high-density genetic map. Front Plant Sci 7: 924.
Lu Y, Lan C, Liang S, Zhou X, Liu D, Zhou G et al. (2009). QTL mapping for adult-plant resistance to stripe rust in Italian common wheat cultivars Libellula and Strampelli. Theor Appl Genet 119: 1349–1359.
Mackay IJ, Bansept-Basler P, Barber T, Bentley AR, Cockram J, Gosman N et al. (2014). An eight-parent multiparent advanced generation inter-cross population for winter-sown wheat: creation, properties, and validation. G3 4: 1603–1610.
Mahuku G, Chen J, Shrestha R, Narro LA, Guerrero KVO, Arcos AL et al. (2016). Combined linkage and association mapping identifies a major QTL (qRtsc8-1), conferring tar spot complex resistance in maize. Theor Appl Genet 129: 1217–1229.
Mott R, Talbot CJ, Turri MG, Collins AC, Flint J . (2000). A method for fine mapping quantitative trait loci in outbred animal stocks. Proc Natl Acad Sci USA 97: 12649–12654.
Sannemann W, Huang BE, Mathew B, Léon J . (2015). Multi-parent advanced generation inter-cross in barley: high-resolution quantitative trait locus mapping for flowering time as a proof of concept. Mol Breed 35: 86.
Sun Z, Li H, Zhang L, Wang J . (2013). Properties of the test statistic under null hypothesis and the calculation of LOD threshold in quantitative trait loci (QTL) mapping. Acta Agron Sin 39: 1–11. (in Chinese with English abstract).
Verbyla AP, George AW, Cavanagh CR, Verbyla KL . (2014a). Whole-genome QTL analysis for MAGIC. Theor Appl Genet 127: 1753–1770.
Verbyla AP, Cavanagh CR, Verbyla KL . (2014b). Whole-genome analysis of multienvironment or multitrait QTL in MAGIC. G3 4: 1569–1584.
Wang J, van Ginkel M, Podlich D, Ye G, Trethowan R, Pfeiffer W et al. (2003). Comparison of two breeding strategies by computer simulation. Crop Sci 43: 1764–1773.
Wang J . (2009). Inclusive composite interval mapping of quantitative trait genes. Acta Agron Sin 35: 239–245. (in Chinese with English abstract).
Wang S, Wen Y, Ren W, Ni Y, Zhang J, Feng J et al. (2016). Mapping small-effect and linked quantitative trait loci for complex traits in backcross or DH populations via a multi-locus GWAS methodology. Sci Rep 6: 29951.
Wei J, Xu S . (2016). A random-model approach to QTL mapping in multiparent advanced generation intercross (MAGIC) populations. Genetics 202: 471–486.
Williams K, Sorrells ME . (2014). Three-dimensional seed size and shape QTL in hexaploid wheat (Triticum aestivum L.) populations. Crop Sci 54: 98–110.
Würschum T, Liu W, Alheit KV, Tucker MR, Gowda M, Weissmann EA et al. (2014). Adult plant development in triticale (× Triticosecale Wittmack) is controlled by dynamic genetic patterns of regulation. G3 4: 1585–1591.
Xu S . (1998). Iteratively reweighted least squares mapping of quantitative trait loci. Behav Genet 28: 341–355.
Zeng Z . (1993). Theoretical basis for separation of multiple linked gene effects in mapping quantitative trait loci. Proc Natl Acad Sci USA 90: 10972–10976.
Zeng Z . (1994). Precision mapping of quantitative trait loci. Genetics 136: 1457–1468.
Zhang L, Li H, Li Z, Wang J . (2008). Interactions between markers can be caused by the dominance effect of QTL. Genetics 180: 1177–1190.
Zhang L, Liu D, Guo X, Yang W, Sun J, Wang D et al. (2010). Genomic distribution of quantitative trait loci for yield and yield-related traits in common wheat. J Integr Plant Biol 52: 996–1007.
Zhang L, Li H, Wang J . (2012). The statistical power of inclusive composite interval mapping in detecting digenic epistasis showing common F2 segregation ratios. J Integr Plant Biol 54: 270–279.
Zhang L, Li H, Ding J, Wu J, Wang J . (2015). Quantitative trait locus mapping with background control in genetic populations of clonal F1 and double cross. J Integr Plant Biol 57: 1046–1062.
Zhu Z, Bonnett D, Ellis M, He X, Heslot N, Dreisigacker S et al. (2016). Characterization of Fusarium head blight resistance in a CIMMYT synthetic-derived bread wheat line. Euphytica 208: 367–375.
Acknowledgements
This work was supported by funding from the National Natural Science Foundation of China (project no. 31671280).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on Heredity website
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Zhang, S., Meng, L., Wang, J. et al. Background controlled QTL mapping in pure-line genetic populations derived from four-way crosses. Heredity 119, 256–264 (2017). https://doi.org/10.1038/hdy.2017.42
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2017.42
This article is cited by
-
Bayesian estimation of multi-allele QTLs for agricultural traits in tomato using recombinant inbred lines derived from two F1 hybrid cultivars
Euphytica (2023)
-
Blib is a multi-module simulation platform for genetics studies and intelligent breeding
Communications Biology (2022)
-
Mapping QTL/QTN and mining candidate genes for plant height and its response to planting densities in soybean [Glycine max (L.) Merr.] through a FW-RIL population
Molecular Breeding (2021)
-
An IBD-based mixed model approach for QTL mapping in multiparental populations
Theoretical and Applied Genetics (2021)
-
Construction and integration of genetic linkage maps from three multi-parent advanced generation inter-cross populations in rice
Rice (2020)