Abstract
In the analysis of DNA sequences on related individuals, most methods strive to incorporate as much information as possible, with little or no attention paid to the issue of statistical significance. For example, a modern workstation can easily handle the computations needed to perform a large-scale genome-wide inheritance-by-descent (IBD) scan, but accurate assessment of the significance of that scan is often hindered by inaccurate approximations and computationally intensive simulation. To address these issues, we developed gLOD—a test of co-segregation that, for large samples, models chromosome-specific IBD statistics as a collection of stationary Gaussian processes. With this simple model, the parametric bootstrap yields an accurate and rapid assessment of significance—the genome-wide corrected P-value. Furthermore, we show that (i) under the null hypothesis, the limiting distribution of the gLOD is the standard Gumbel distribution; (ii) our parametric bootstrap simulator is approximately 40 000 times faster than gene-dropping methods, and it is more powerful than methods that approximate the adjusted P-value; and, (iii) the gLOD has the same statistical power as the widely used maximum Kong and Cox LOD. Thus, our approach gives researchers the ability to determine quickly and accurately the significance of most large-scale IBD scans, which may contain multiple traits, thousands of families and tens of thousands of DNA sequences.
Similar content being viewed by others
Introduction
After performing a genome-wide inheritance-by-descent (IBD) scan, researchers are often faced with the following dilemma: ‘Should I run a time consuming simulation to get an accurate estimate of the genome-wide corrected (that is, adjusted) P-value, or should I approximate the adjusted P-value, which is quick but less powerful (that is, conservative)?’ To understand why these two choices arise, recall that under the null hypothesis of independent assortment, the expected proportion of alleles shared IBD between two individuals depends only on their biological relationship (Kong and Cox, 1997; Kruglyak and Lander, 1998; Bacanu, 2005). As this expected proportion increases among affected relative pairs at disease-related loci, scanning the genomes of affected relatives for evidence of increased sharing IBD has the potential to identify genetic factors that increase risk for disease. However, measuring the strength of that evidence is problematic because accurate adjusted P-values usually require computationally intensive simulation because either the limiting distribution of the multi-marker IBD test or the multiple tests correction is unknown, and because estimates based on theoretical approximations are typically conservative and study-specific. The undesirable characteristics of theoretical approximations are unavoidable because the suggested thresholds (Lander and Kruglyak, 1995) are based upon several unmet assumptions: fully informative matings, homogeneous relationships among affected family members (for example, affected sibling pairs (ASP)) and an infinite sample size (that is, the theory of large deviations).
Gene dropping is arguably the most common approach for estimating accurate P-values, but this approach requires specialized and computationally intensive software like MERLIN (Abecasis et al., 2002), Genedrop (Wijsman et al., 2006), Markerdrop (Thompson, 1994; Heath et al., 1997), Haplodrop (Stewart and Subaran, 2012), Caleb (Greenberg, 2011) or Genehunter (Kruglyak and Lander, 1998). Typically, the computational demands associated with gene dropping (GD) include, but are not limited to, enumerating inheritance vectors, identifying cut sets, computing pedigree likelihoods and finding efficient peeling sequences. As many of these bottlenecks are intrinsic to the computation for a single multi-marker IBD scan, analysis of each simulated replicate (as opposed to replicate generation) often consumes a larger fraction of the total time needed to compute the adjusted P-value. In fact, when the analysis programs make use of all of the available data (for example, EAGLET (Stewart et al., 2010; Stewart et al., 2011, 2013; Kambhampati et al., 2013) and MORGAN (Thompson, 1994; Heath et al., 1997)), the total computation time can increase substantially. Thus, the conceptual simplicity of the GD approach is often outweighed by its computational complexity—even for modern IBD scans that typically contain a large number of small (that is, computationally less complex) families.
Approximating the adjusted P-value is an alternative to GD. Although this approach typically provides the answer immediately, methods that approximate the adjusted P-value are often study-specific (for example, affected sib pairs, affected cousin pairs, grand-parent grand-child pairs and so on) and conservative owing to the fact that the underlying assumptions (for example, an infinite number of markers with fully informative matings at each marker (Feingold et al., 1993; Lander and Kruglyak, 1995)) are often unrealistic. As those assumptions are routinely violated in practice, the approximate adjusted P-value is upwardly biased and the power is reduced. Furthermore, any test that uses the approximation approach is sensitive to the degree to which those assumptions are violated (that is, the test becomes increasingly conservative as the number of markers decreases and/or as the informativeness of each mating decreases).
Bacanu (2005) proposed DAR, an approximation method that models marker-specific IBD statistics as an AR(1) autoregressive process. This method uses a moment-based estimator of the correlation between successive linkage statistics (as opposed to the maximum likelihood estimator), and it also uses a mathematical approximation to the tail probabilities of a bivariate normal distribution to estimate the adjusted P-value. As we will show in Results, DAR works well when the matings at each marker are fully informative (that is, when the assumed AR(1) model is correct) and when the correlation is not too close to one, but performance tends to deteriorate in more realistic settings, especially as the amount of missing data increases.
To avoid the aforementioned drawbacks of GD and approximation methods while simultaneously capitalizing on the strengths of the AR(1) model (for example, speed and potentially accuracy), we have developed gLOD—a new test for co-segregation that implements a maximum likelihood estimate of correlation to permit rapid computation of accurate adjusted P-values. In the context of IBD scans computed from dense single nucleotide polymorphism (SNP) data on affected families, our test is robust to heterogeneous family structures and missing genotype data. Furthermore, by exploiting the theory of stationary Gaussian processes, we show (for the first time) that a multi-marker IBD statistic (that is, the gLOD) has a limiting distribution under the null hypothesis; both the gLOD and the maximum Kong and Cox LOD (Kong and Cox, 1997) have the same statistical power. Because of its speed and generality, and because power is maintained, the gLOD should facilitate the analysis of any large-scale multi-marker IBD scan, especially scans that contain multiple traits, thousands of families and tens of thousands of DNA sequences. Our proposed test and our high-speed simulator are freely available from the web at: http://www.mathmed.org/wclstewart/HOME/SOFT/soft.html.
Methods
The maximum Kong and Cox IBD statistic (denoted by Kn,m) is defined as

where m is the total number of markers of interest across the genome, L(δ;Dn,m) is the Kong and Cox likelihood (Kong and Cox, 1997) and Dn,m are the multilocus genotype and phenotype data of n affected families. For each marker, the Kong and Cox likelihood is indexed by a single univariate parameter, δ, which quantifies the departure from independent assortment. The maximum likelihood estimate of δ is denoted by  . Now, because
. Now, because

and because  is asymptotically normal with mean zero (under the null hypothesis), it follows that Kn,m>0 for large n and m (that is, Pr(Kn,m>0)→1 as n,m→∞). With this notation, our proposed test (that is, the gLOD) is
is asymptotically normal with mean zero (under the null hypothesis), it follows that Kn,m>0 for large n and m (that is, Pr(Kn,m>0)→1 as n,m→∞). With this notation, our proposed test (that is, the gLOD) is

where the coefficients cm=(2lnm)1/2 and bm=cm−ln(4π⋅lnm)/(2cm) ensure convergence in distribution of Tn,m for large n and m. Furthermore, because the Kong and Cox LOD rejects the null hypothesis when Kn,m>a∈ R+ the rejection region for Tn,m is (cm[(2 ln(10)⋅a)1/2−bm],∞), and because cm[(2 ln(10)⋅a)1/2−bm] is one-to-one and surjective (that is, ‘onto’) with respect to these two rejection regions, Tn,m and Kn,m have the same statistical power.
To the best of our knowledge, our test Tn,m is the first multi-marker IBD statistic with a known limiting distribution under the null hypothesis. In particular, if z≡(z1,...,zm) is a stationary Gaussian process with zt~N(0,1), then as m→∞, Berman (1964) showed that

converges in distribution to F(w)=exp(−e−w), which, in accordance with the Fisher-Tippett extreme value theorem, is also the limiting distribution if the zt are independent.
As  is asymptotically normal with mean zero and unit variance under the null hypothesis, it follows that Tn,m converges to Fas n,m→∞. However, the rate of convergence can be slow (that is, the rate is no faster than 1/logm (Hall, 1979)), especially for modern genome-wide linkage studies where the correlation between zt and zt+1 is typically close to one. In practice, Fn,m (that is, the finite sampling distribution of Tn,m) is quite far from F, and to accurately determine the significance of Tn,m, one must again resort to simulation. However, because Fn,m is converging to Fm, we can accurately estimate the adjusted P-value for large samples by simulating from a distribution that is close (if not equal) to Fm. Moreover, because Tn,m is just a simple function of normally distributed (but correlated) random variables (as opposed to a computationally intensive function of multilocus genotypes), our proposed approach for estimating the adjusted P-value is roughly 40 000 times faster than GD.
is asymptotically normal with mean zero and unit variance under the null hypothesis, it follows that Tn,m converges to Fas n,m→∞. However, the rate of convergence can be slow (that is, the rate is no faster than 1/logm (Hall, 1979)), especially for modern genome-wide linkage studies where the correlation between zt and zt+1 is typically close to one. In practice, Fn,m (that is, the finite sampling distribution of Tn,m) is quite far from F, and to accurately determine the significance of Tn,m, one must again resort to simulation. However, because Fn,m is converging to Fm, we can accurately estimate the adjusted P-value for large samples by simulating from a distribution that is close (if not equal) to Fm. Moreover, because Tn,m is just a simple function of normally distributed (but correlated) random variables (as opposed to a computationally intensive function of multilocus genotypes), our proposed approach for estimating the adjusted P-value is roughly 40 000 times faster than GD.
To obtain realizations from a distribution that is close (if not equal) to Fm, we use the parametric bootstrap (PB) (Efron and Tibshirani, 1993). For ease of exposition, we restrict attention to a single chromosome with the understanding that the extension to k independent chromosomes (for example, the entire genome) is straightforward. Under the null hypothesis, we assume that the vector:  follows an AR(1) autoregressive model for t=1,…,m. Thus, the log-likelihood function is:
follows an AR(1) autoregressive model for t=1,…,m. Thus, the log-likelihood function is:

where  and Σρ is the usual variance-covariance matrix for an AR(1) process that depends only on the correlation ρ. We maximize this log-likelihood to obtain the maximum likelihood estimator–MLE(ρ), and for each realization z*, we use Equation (2) to compute Tm*. Here, the asterisk superscript implies that the corresponding random variable is realized from the PB procedure. Hence, the proportion of replicates that exceed the observed value of Tn,m accurately estimates the adjusted P-value.
and Σρ is the usual variance-covariance matrix for an AR(1) process that depends only on the correlation ρ. We maximize this log-likelihood to obtain the maximum likelihood estimator–MLE(ρ), and for each realization z*, we use Equation (2) to compute Tm*. Here, the asterisk superscript implies that the corresponding random variable is realized from the PB procedure. Hence, the proportion of replicates that exceed the observed value of Tn,m accurately estimates the adjusted P-value.
Data description
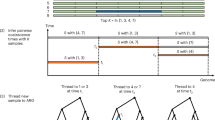
To compare the type 1 error rates of our proposed test (gLOD) with three competing methods, we simulated genome-wide equi-frequent marker data for nuclear families under the null hypothesis of independent assortment. We considered three scenarios: (i) each family has four members, and each member provides complete microsatellite data (CMD); (ii) only the ASP provides SNP data; and (iii) a scenario (denoted MIX) that contains a mixture of nuclear families of varying informativeness, with some families providing SNP genotypes for every member, while other families have missing genotype data on one or both parents (see Figure 1 for a detailed description of the pedigree structures that were used). Across all scenarios, only offspring provided phenotypic data, and every family contained at least one ASP.
Pedigree structures (A–D) are shown, where individuals shaded in black are both affected and genotyped, gray are genotyped only and unshaded individuals are neither phenotyped nor genotyped. Each replicate contained 400 families of type (A and D), or a mixture of types (A–D) in the following proportions: 52, 23, 15 and 10 percent, respectively.
Conceptually, the CMD scenario represents the ideal situation where IBD information is completely known. In CMD, adjacent microsatellites are separated by 5 centiMorgans (cMs), and each microsatellite has 20 alleles. By contrast, the ASP scenario is intended to represent the worst case. The MIX scenario falls somewhere in between CMD and ASP. In the ASP, and MIX scenarios, SNPs are separated by 1 cM for a total of 3484 SNPs across the genome. For each scenario, we simulated 5000 replicates (via GD) with 400 families per replicate, and for each replicate, we estimated the actual type 1 error using: (i) 10 000 PB realizations, (ii) a tail probability approximation (denoted DAR) and (iii) the limiting Gumbel distribution (GUMBEL). Finally, to demonstrate the utility of our proposed test when applied to real data, we computed the gLOD from the genome-wide dense SNP data of 422 type 1 diabetic families.
Results
For each replicate and for each competing method: PB, DAR and GUMBEL, we used GD to estimate the actual type 1 error, the absolute bias from the nominal type 1 error, the standard deviation and the root mean squared error. Results are shown for a nominal genome-wide corrected type 1 error of 5%, but qualitatively, the relative behavior of all three methods for 10% and 1% type 1 error rates is unchanged (data not shown).
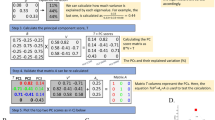
With the CMD scenario, where the autoregressive model is correct because IBD information is known, we see that there is good agreement (Table 1) between our proposed PB approach and DAR (the tail probability approximation). This is expected because both methods assume an underlying AR(1) model, and because both methods yield virtually identical estimates of the autocorrelation  , which is not too close to one. Note that type 1 error estimates derived from the limiting Gumbel distribution (denoted GUMBEL) do not depend on an estimate of the autocorrelation, nor do they depend on an estimate of the finite sampling distribution. Therefore, standard deviations and root mean squared errors are not applicable for GUMBEL estimates of the type 1 error.
, which is not too close to one. Note that type 1 error estimates derived from the limiting Gumbel distribution (denoted GUMBEL) do not depend on an estimate of the autocorrelation, nor do they depend on an estimate of the finite sampling distribution. Therefore, standard deviations and root mean squared errors are not applicable for GUMBEL estimates of the type 1 error.
Although the AR(1) assumption is no longer correct in the ASP scenario, it still provides a reasonable first-order approximation to the distribution of normally distributed (but correlated) IBD statistics across the genome. This is shown by the fact that, for a nominal family-wise type 1 error of 5%, the PB estimate of the genome-wide type 1 error is 4.31% (Table 2). Moreover, the approximation provided by our PB approach is roughly 40 000 times faster than DAR. Specifically, the simulation and analysis of a single GD replicate in the ASP setting takes ~38 s on a 3.4 GHz processor. On the same machine and in the same amount of time, one can simulate and analyze more than 40 000 PB replicates.
As the DAR method also assumes an underlying AR(1) model, one might expect to find similar performance between DAR and the gLOD. However, the DAR-based estimate of the genome-wide type 1 error (3.69%) is less accurate than the estimate obtained by the gLOD. This happens because the tail probability approximation and the autocorrelation estimator in DAR are both sensitive to autocorrelations near 1.0. As our PB approach uses maximum likelihood to estimate the autocorrelation, it is less sensitive to autocorrelations near 1.0. For the ASP scenario, the autocorrelation as estimated by DAR is 0.991 and as estimated by the gLOD is 0.985. Furthermore, because the genome length is fixed, the GUMBEL estimator of type 1 error is also sensitive to autocorrelations close to 1.0, because high autocorrelation is equivalent to a reduction in ‘effective’ sample size (that is, the finite sampling distribution is far from the limiting Gumbel distribution). For example, it is considerably more conservative in the ASP scenario (genome-wide type 1 error=0.12%) than it is in the CMD scenario (genome-wide type 1 error=3%).
In the more realistic scenario (denoted MIX), the data contain a mixture of nuclear families with differing amounts of missing SNP data and different sibship sizes. However, PB still outperforms both DAR and GUMBEL (Table 3). In fact, because the theoretical basis for the GUMBEL estimator is quite similar to the conservative approximation first advanced by Kruglyak and Lander (1998), it is not surprising that the two methods yield similar type 1 error approximations. Recall that the Krugyak and Lander approach recommends rejecting the null hypothesis when the uncorrected P-value is less than 2.2 × 10−5. For the MIX scenario, this recommendation equates to an actual genome-wide type 1 error of 0.7%, which is quite close to the GUMBEL estimates of 0.8% and 0.9% (Tables 2 and 3). For the MIX scenario, the autocorrelation as estimated by DAR is 0.989, and as estimated by the gLOD is 0.981.
It is not surprising (given the mathematical relationship between type 1 error and power) that GD has slightly higher power than PB, and that PB has slightly higher power than DAR and that all three are considerably more powerful than GUMBEL. In terms of power, the relative performance of all four methods remained unchanged for the three instructive scenarios shown here, and for a wider range of trait models and pedigree structures (data not shown). Because the null and alternative distributions are fixed, any testing procedure that overestimates the critical value (for example, PB, DAR and GUMBEL) must have lower power than the one that does not (for example, GD).
We also tested the method using real data by analyzing 422 type 1 diabetic families with our PB approach. Using this approach, we estimated the adjusted P-value at less than 1e-05, which occurred directly over the HLA (Human Leukocyte Antigen) region (a small stretch of chromosome 6 that explains most of the heritability of type 1 diabetes). Interestingly, the second highest peak (Kong and Cox LOD=2.67) occurs on chromosome 2 at SNP rs1533661. This SNP is 7 megabases from CTLA4 (cytotoxic T-lymphocyte-associated protein 4), a gene known to influence type 1 diabetes (Nisticò et al., 1996) and other autoimmune disorders (Ban et al., 2003) as well. Arguably, the unadjusted P-value (0.0002) for rs1533661 is suggestive, but it is the gLOD that correctly quantifies the evidence for this SNP’s influence by providing an adjusted P-value of 0.18. Thus, in addition to detecting suggestive loci, the gLOD makes it easier to interpret their overall statistical importance as well.
Discussion
Our approach provides fast and accurate P-values for multi-marker IBD scans, and it maintains the same statistical power as the commonly used Kong and Cox LOD. Furthermore, our PB approach yields critical values for testing that are less conservative than published guidelines, and our approach can be applied to a wider variety of study designs as well. Its speed, accuracy and generality should allow independent labs to compare and combine their multi-marker IBD results quickly, confidently and more easily.
Compared with GD (denoted  ), our PB approach (denoted
), our PB approach (denoted  ) is extremely fast, and this was certainly our primary motivation for developing the proposed simulator. However, because the misfit between
) is extremely fast, and this was certainly our primary motivation for developing the proposed simulator. However, because the misfit between  and Fm (when it exists) could in principle be important, we extended our AR(1) model to a second-order Markov assumption (that is, we modeled the conditional distribution of zt+2 given zt+1 and zt), and recomputed the actual type 1 errors for PB and DAR. The results from this sensitivity analysis were qualitatively the same (data not shown), suggesting that the AR(1) model is at least adequate for most modern IBD scans. We are currently working to extend our test statistic to detect protective loci, and to incorporate the phenotypes of unaffected individuals into the analysis.
and Fm (when it exists) could in principle be important, we extended our AR(1) model to a second-order Markov assumption (that is, we modeled the conditional distribution of zt+2 given zt+1 and zt), and recomputed the actual type 1 errors for PB and DAR. The results from this sensitivity analysis were qualitatively the same (data not shown), suggesting that the AR(1) model is at least adequate for most modern IBD scans. We are currently working to extend our test statistic to detect protective loci, and to incorporate the phenotypes of unaffected individuals into the analysis.
To the best of our knowledge, gLOD is the first genome-wide, multi-marker IBD statistic that has been shown to have a limiting distribution under the null hypothesis. Given that so many different IBD statistics have comparable power, it is likely that many of these tests also have similar limiting distributions as well. This conjecture is further supported by the recent report that the asymptotic behavior of the maximum multipoint LOD for two fully informative and linked markers (where the maximization is not restricted to the genetic length of a DNA molecule, but instead occurs over the entire real line appears to converge to a non-degenerate distribution under the null hypothesis (Hodge et al., 2008)). If there are other multi-marker IBD statistics with limiting distributions, then it may be possible to select statistics so as to maximize power, and/or the rate of convergence, and/or robustness to the presence of missing data.
For the first time, thanks to our proposed test (that is, the gLOD) and to our PB approach, standardization of IBD scans across studies is a real possibility. Ultimately, the gLOD could significantly improve the fine-mapping of linked regions, which in turn should increase the power of re-sequencing methods. Overall, our approach gives researchers the ability to quickly and accurately determine the significance of a modern IBD scan without having to sacrifice statistical power.
Data archiving
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.7tb57.
References
Abecasis GR, Cherny SS, Cookson WO, Cardon LR . (2002). Merlin—rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet 30: 97–101.
Bacanu SA . (2005). Robust estimation of critical values for genome scans to detect linkage. Genet Epidemiol 28: 24–32.
Ban Y, Davies TF, Greenberg DA, Kissin A, Marder B, Murphy B et al. (2003). Analysis of the CTLA-4, CD28, and inducible costimulator (ICOS) genes in autoimmune thyroid disease. Genes Immun 4: 586–593.
Berman SM . (1964). Limit theorems for the maximum term in stationary sequences. Annals of Mathematical Statistics 35: 502–516.
Efron B, Tibshirani RJ . (1993) An Introduction to the Bootstrap. Chapman & Hall: New York, NY, USA.
Feingold E, Brown PO, Siegmund D . (1993). Gaussian models for genetic linkage analysis using complete high-resolution maps of identity by descent. Am J Hum Genet 53: 234–251.
Greenberg DA . (2011). Computer simulation is an undervalued tool for genetic analysis: a historical view and presentation of SHIMSHON—a Web-based genetic simulation package. Hum Hered 72: 247–257.
Hall P . (1979). On the rate of convergence of normal extremes. Journal of Applied Probability 16: 433–439.
Heath SC, Snow GL, Thompson EA, Tseng C, Wijsman EM . (1997). MCMC segregation and linkage analysis. Genet Epidemiol 14: 1011–1016.
Hodge SE, Rodriguez-Murillo L, Strug LJ, Greenberg DA . (2008). Multipoint lods provide reliable linkage evidence despite unknown limiting distribution: type I error probabilities decrease with sample size for multipoint lods and mods. Genet Epidemiol 32: 800–815.
Kambhampati S, Stewart C, Stewart W, Kelley J, Ramnath R . (2013). Managing tiny tasks for efficient, data-parallel subsampling. The Second IEEE Conference on Cloud Engineering.
Kong A, Cox NJ . (1997). Allele-sharing models: LOD scores and accurate linkage tests. Am J Hum Genet 61: 1179–1188.
Kruglyak L, Lander ES . (1998). Faster multipoint linkage analysis using Fourier transforms. J Comput Biol 5: 1–7.
Lander E, Kruglyak L . (1995). Genetic dissection of complex traits: guidelines for interpreting and reporting linkage results. Nat Genet 11: 241–247.
Nisticò L, Buzzetti R, Pritchard LE, Van der Auwera B, Giovannini C, Bosi E et al. (1996). The CTLA-4 gene region of chromosome 2q33 is linked to, and associated with, type 1 diabetes. Belgian Diabetes Registry. Hum Mol Genet 5: 1075–1080.
Stewart WC, Subaran RL . (2012). Obtaining accurate p values from a dense SNP linkage scan. Hum Hered 74: 12–16.
Stewart WCL, Drill EN, Greenberg DA . (2011). Finding disease genes: a fast and flexible approach for analyzing high-throughput data. Eur J Hum Genet 19: 1090–1094.
Stewart WCL, Huang Y, Greenberg DA, Vieland VJ . (2013). Next generation linkage and association methods applied to hypertension: a multi-faceted approach to the analysis of sequence data. BMC Proc 8: S1–S111.
Stewart WCL, Peljto AL, Greenberg DA . (2010). Multiple subsampling of dense SNP data localizes disease genes with increased precision. Hum Hered 69: 152–159.
Thompson EA . (1994). Monte Carlo likelihood in the genetic mapping of complex traits. Philos Trans R Soc Lond B Biol Sci 344: 345–350; discussion 350-341.
Wijsman EM, Rothstein JH, Thompson EA . (2006). Multipoint linkage analysis with many multiallelic or dense diallelic markers: Markov chain-Monte Carlo provides practical approaches for genome scans on general pedigrees. Am J Hum Genet 79: 846–858.
Acknowledgements
We would like to thank Dr Susan E Hodge, Dr David A Greenberg and the Referees for their thoughtful comments and remarks during the preparation and review of this manuscript. Access to the diabetes data used in the analysis was generously given by the National Disease Resource Interchange, Philadelphia, PA.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Stewart, W., Hager, V. A powerful test of independent assortment that determines genome-wide significance quickly and accurately. Heredity 117, 109–113 (2016). https://doi.org/10.1038/hdy.2016.33
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2016.33