Abstract
The study of the dispersal capability of a species can provide essential information for the management and conservation of its genetic variability. Comparison of gene flow rates among populations characterized by different management and evolutionary histories allows one to decipher the role of factors such as isolation and tree density on gene movements. We used two paternity analysis approaches and different strategies to handle the possible presence of genotyping errors to obtain robust estimates of pollen flow in four European beech (Fagus sylvatica L.) populations from Austria and France. In each country one of the two plots is located in an unmanaged forest; the other plots are managed with a shelterwood system and inside a colonization area (in Austria and France, respectively). The two paternity analysis approaches provided almost identical estimates of gene flow. In general, we found high pollen immigration (∼75% of pollen from outside), with the exception of the plot from a highly isolated forest remnant (∼50%). In the two unmanaged plots, the average within-population pollen dispersal distances (from 80 to 184 m) were higher than previously estimated for beech. From the comparison between the Austrian managed and unmanaged plots, that are only 500 m apart, we found no evidence that either gene flow or reproductive success distributions were significantly altered by forest management. The investigated phenotypic traits (crown area, height, diameter and flowering phenology) were not significantly related with male reproductive success. Shelterwood seems to have an effect on the distribution of within-population pollen dispersal distances. In the managed plot, pollen dispersal distances were shorter, possibly because adult tree density is three-fold (163 versus 57 trees per hectare) with respect to the unmanaged one.
Similar content being viewed by others
Introduction
Maintaining genetic diversity within a population heavily depends on genetic connectivity with surrounding populations. Moreover, the adaptability of a population to climate or anthropic changes is enhanced by the arrival of genes from areas where present climatic conditions mimic future ones (Jump and Peñuelas, 2005). It is known that forest trees show extensive gene flow, especially when pollen or seeds are wind-dispersed (for example, Robledo-Arnuncio and Gil, 2005; Piotti et al., 2009; Williams, 2010). This statement has been largely based on the fact that, until now, gene flow was mainly studied by means of indirect genetic methods (that is, Fst-based methods) or inferred from the comparison of genetic variability measures (see Aguilar et al., 2008; Eckert et al., 2008, and references therein). The thus obtained patterns are the result of population past evolutionary histories and do not shed light on current gene flow patterns. On the contrary, direct methods (that is, paternity and parentage analyses) provide accurate estimates of contemporary gene flow (Jones and Ardren, 2003). Such estimates allow detecting instantaneous signals produced by current conditions characterizing a population. Different analytical approaches are currently available to study contemporary gene flow. They differ in rationale, assumptions on the genetic variability of the background population and ways to handle possible errors due to low discriminatory power of the marker set or the presence of genotyping errors (Burczyk and Chybicki, 2004; Slavov et al., 2005; Jones et al., 2010). Recent methodological improvements allow to estimate the statistical precision of a parentage/paternity assignment for a given sample of a reproductive population (Gerber et al., 2003; Burczyk and Chybicki, 2004). In any case, both Oddou-Muratorio et al. (2003) and Bacles and Ennos (2008) claimed that it is better to use several approaches together to estimate genetic exchange among populations.
Contemporary gene flow estimates can vary greatly among populations for the same species. Hoebee et al. (2007) comparing pollen flow patterns between a small, isolated population and a large, continuous population of Sorbus torminalis found differences in the pollination distance curve, the self-pollination rate and the number of contributing fathers per progeny. In particular, they showed a substantial pollen immigration reduction in the smaller, and more isolated, population (∼4 versus ∼38%). Similarly, Slavov et al. (2009) recorded discrepancies in immigration rates, pollen pool differentiation among mothers and male neighbourhood sizes between two ecologically contrasting populations of Populus trichocarpa. Thus it is far-fetched to conclude that what is recorded in a single study conducted in a single stand is the gene flow rate characteristic of a species.
The number of publications comparing gene flow patterns between different conditions is increasing. However, to date the comparison of contemporary gene flow rates between managed and unmanaged forest tree stands is almost unexplored (Robledo-Arnuncio et al., 2004). Silvicultural treatments may modify the amount of genetic variability and the spatial genetic structure within a stand (Rajora, 1999; Rajora et al., 2000; Takahashi et al., 2000), suggesting possible changes in gene flow patterns within and among stands. These results were usually obtained by monitoring the levels and spatial distribution of genetic variability. However, in forest trees these population parameters are usually not modified by human activities in the short term, but their effects are delayed for a few generations because of long generation time (Kramer et al., 2008). By contrast, silvicultural treatments may rapidly modify the density and the effective population size of the stands and, therefore, contemporary gene flow patterns. Nevertheless, generalizations should be treated with caution considering that the life history and reproductive biology of each species also have an important role (El-Kassaby and Benowicz, 2000).
In this study, we used both mating model and maximum likelihood paternity analysis to analyse pollen flow patterns in four European beech (Fagus sylvatica L.) populations characterized by different management and evolutionary histories. In both approaches the estimated frequencies of null alleles were taken into account in order to minimize possible confounding factors in gene flow estimation. Our results contribute to clarify the role of factors such as isolation and management on gene movement within and among populations, and, therefore, on shaping future genetic diversity. In addition, to provide a complete picture of gene flow dynamics for this species, we studied (i) the relationship between potentially significant phenotypic characteristics of sampled trees (location, diameter, height, crown area, bud burst phenology) and their reproductive success; and (ii) the distribution of within-population pollen dispersal distances and the occurrence of long-distance dispersal events.
Materials and methods
Study sites, sample collection and microsatellite analysis
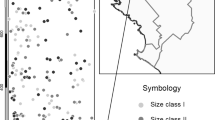
To study pollen flow in beech, four plots were chosen among the 10 described by Buiteveld et al. (2007) from the Dynabeech project (Kramer, 2004) (Table 1). Two plots (Dobra-1 and Dobra-2; Figures 1a and b) are located in Austria, in the Waldviertel region, in close proximity to each other (500 m). Dobra-1 (coded as D1; see Table 1) is inside an untouched area, whereas Dobra-2 (D2) has been managed following the shelterwood system, with a rotation length of 100–120 years and a seeding cut 10–15 years before harvesting, combined with natural regeneration. The third and fourth plots (Figures 1c and d) are located in Southern France on the St Baume Mountain (SB) and on the northern slope of Ventoux Mountain (VE), approximately 100 km apart. VE is located in a recently colonized area. SB is located inside a large natural population that nowadays is a beech gene conservation unit. The entire population is isolated from the next one at least by 60 km (see Figure 2 in Delhon and Thiébault, 2005), and it is considered a relic population that originated in the Pre-boreal from a refugium south of the actual Rhone delta. A detailed description of the four plots is given in Buiteveld et al. (2007), and a summary of their main characteristics is reported in Table 1.
In total, 803 adult trees and 1009 seeds (from 27 trees, hereafter referred to as maternal trees) were sampled; 376 trees and 447 seeds from the French stands in year 1999, and 427 trees and 562 seeds from the Austrian stands in the year 2000 (Table 1). All adult trees present in the four stands were sampled for genetic analysis and mapped. A detailed phenotypic characterization was conduced for all individuals in the Austrian stands: diameter at breast height (DBH), height, crown radius and crown height were measured. Moreover, bud burst phenology was recorded from 2001 to 2003 and was used as a proxy for flowering phenology, given the simultaneous development of leaves and flowers (Becker, 1981, p. 43). Observations were conducted every 2 days and phenological stages were assessed following an adaptation of Malaisse's scale, considering stage 5 as the critical stage (Malaisse, 1967; Teissier du Cros et al., 1981).
Four highly polymorphic microsatellites (FS1-15, FS4-46, FS3-04 and mfc5 for samples from Austrian stands, and FS1-15, FS4-46, FS1-25 and mfc5 for samples from French stands) developed in beech by Pastorelli et al. (2003) and Tanaka et al. (1999) were used to genotype all individuals. These microsatellites were selected because they showed Mendelian inheritance, a high level of polymorphism (Pastorelli et al., 2003) and because they were unlinked (Scalfi et al., 2004). PCR amplifications were performed following the conditions reported in Pastorelli et al. (2003) and fragment size detection was conducted as described by Buiteveld et al. (2007). To rule out amplification failure due to laboratory errors or poor DNA quality, PCR was performed at least twice on samples without any amplification product, and DNA was re-isolated when amplification failure was systematic across loci (Oddou-Muratorio et al., 2009).
Data analysis
The frequencies of genotyping errors in the four data sets were assessed by calculating a genotyping error rate quantified by direct comparison of offspring–mother genotype at each locus and averaged over loci. In addition, the frequencies of null alleles were directly estimated by using the program INEst, running the individual inbreeding model (IIM) with a Gibbs sampler of 105 iterations (Chybicki and Burczyk, 2009a). An estimate of null allele frequencies in the data sets from French stands based on different approaches was also conducted by Oddou-Muratorio et al. (2009).
To take into account possible genotyping errors during microsatellite scoring, we accommodated loci for which the presence of null alleles was suspected, and performed parentage analysis following different approaches, as suggested in recent literature (Bacles and Ennos, 2008; Oddou-Muratorio et al., 2009).
As by Bacles and Ennos (2008), instead of introducing in the analysis a global stochastic error rate, we performed two subsequent transformations of the original data sets (referred to hereafter as RAW data sets): a binning procedure for allele miscalls (obtaining the BIN data sets) and a subsequent genotype substitution procedure for allele dropouts (BINNULL data sets). In the binning procedure all alleles with frequency below 0.01 were binned with alleles >0.01 of the nearest size. In the genotype substitution procedure, homozygous genotypes were systematically changed into heterozygotes with a null allele, and non-amplifying genotypes were transformed into null allele homozygotes. For every locus in each population, the transformation that guaranteed the higher paternity exclusion probability (EPP) and lower genotyping error (calculated for each locus as the number of mother–offspring mismatches divided by the number of possible comparisons) was retained to build the final data set for paternity analysis (MINERROR data sets). For loci where no significant improvements were achieved after transformation, the raw data were used.
Paternity analysis was conducted by using both a maximum likelihood approach (Gerber et al., 2000) and a mating model approach (Burczyk et al., 2002). The maximum likelihood approach is aimed at assigning paternity to each analysed seed and allows one to estimate individual reproductive success of local adults, whereas by the mating model approach dispersal parameters and selection gradients at the population level (and their confidence intervals) are jointly estimated.
The maximum likelihood paternity analysis was conduced on the four MINERROR data sets (one for each plot) by using the software FaMoz (Gerber et al., 2003), following a categorical allocation approach (Jones et al., 2010) based on the assignment of paternity to the individual with the highest LOD score above an estimated thresholds. Seeds were considered as locally pollinated if at least one compatible father with a logarithm of odds (LOD) score above the threshold was found, otherwise they were classified as pollinated by external trees. The thresholds for statistical significance of LOD scores were estimated by following the simulation method described by Gerber et al. (2000). The distribution of the LOD scores of the most likely fathers of 50 000 seeds randomly generated from the genotypes of local adult trees and the distribution of LOD scores of the most likely fathers of 50 000 seeds whose paternal genotype was randomly generated according to allele frequencies were graphically compared. The threshold for paternity assignment was chosen at the intersection of the two distributions of LOD scores to minimize both type-I (that is, when a seed pollinated by local pollen is not assigned to local fathers) and type-II error (that is, when a paternity is attributed to a local father, whereas the true father is outside the sampling area) (Gerber et al., 2000). LOD scores were calculated by accounting for a mistyping error (e) set to 0 and for mean departures from Hardy–Weinberg equilibrium estimated from the data.
The mating model paternity analysis was performed by using the neighbourhood model, originally introduced by Adams and Birkes (1991) and extended by Burczyk et al. (2002), implemented in the program NM+ (Chybicki and Burczyk, 2010a). The program allows estimating parameters of the neighbourhood model taking into account the estimated null allele frequencies for each scored locus. The analysis was run on each RAW data set by using the default value for the neighbourhood size and the ‘stop’ criterion (inf and 0.001, respectively), and introducing null allele frequencies resulting from INEst analysis. The estimated parameters were the pollen immigration (mp), selfing rate (s), shape (bp) and scale (δp) parameters of four families of testable dispersal kernels (exponential power, Weibull, geometric and 2Dt), and selection gradients for covariates of the reproductive success (γcrown_area for crown area, γheight for height and γdbh for diameter). The models based on different dispersal kernels were compared and the one with the highest final log-likelihood was chosen as the most representative (Chybicki and Burczyk, 2009b).
Once paternity was assessed by following maximum likelihood paternity analysis, we determined and explored the distributions of pollen dispersal events for the four plots. Pollination distances were calculated as the Euclidean distance between pollen donors and maternal trees. When two (or more) pollen donors with the same LOD scores were the most likely ones, the mean of their distances from the maternal tree was considered as the pollination distance. To determine whether pollen dispersal distribution resembles the distribution of distances between all potential pollen donors and maternal trees, we compared them in each stand by using a Kolmogorov–Smirnov test (Sokal and Rohlf, 1995).
To study factors affecting male reproductive success estimated by the maximum likelihood paternity analysis, we ran two Generalized Linear Model analyses (McCullagh and Nelder, 1989) on the data sets from the Austrian stands, where a detailed phenotypic characterization of all adult trees was available. Data from D1 and D2 were pooled because we found no evidence of plot influence on reproductive success. In the first analysis we used the female-specific male reproductive success as dependent variable, which is estimated as the number of assigned paternities for each male with each sampled female over the total number of seeds analysed for each sampled female. A binomial (successful pollinations versus unsuccessful pollinations of each male–female pair) distribution of errors was assumed. The independent variables were the distance, the angle (calculated as described by Burczyk et al., 1996) and the degree of phenological overlap between the potential pollen donor and the maternal tree, the DBH, the height and the crown area (assuming a surface of cylindrical shape with crown height as height and crown radius as radius) of each potential pollen donor. Flowering phenology overlap was computed by assuming that female flower receptivity and male flower pollen shedding start at the day of bud burst and last for 10 days. According to this, individual flowering behaviour was modelled for every tree fitting a normal curve by using the fifth day after bud burst as the mean, and the first and tenth days as the 0.05 and 0.95 quantiles, respectively. Flowering overlap between two individuals was consequently calculated as the area of overlap between two normal curves describing the flowering behaviour of two trees. The average of phenological overlap over the 3 years was then used.
In the second analysis we used as dependent variable the total male reproductive success (assigned paternities) over all sampled maternal trees, and a Poisson distribution of errors, which is usually considered more suitable for count data, was assumed. The independent variables were DBH, height, crown area of each potential pollen donor and the number of ‘nearby maternal trees’ sampled. Given that the definition of ‘nearby maternal trees’ is arbitrary, we counted the number of sampled maternal trees located within a circle centred on each male, with radius of 10 m, 20, 30 and so on, up to 140 m.
All analyses were run by using the glm function of the R statistical package (R Development Core Team, 2010), starting from the model with all independent variables included and gradually simplifying the model by dropping the non-significant ones (Crawley, 2002).
Results
Genetic variability was high in all study areas (Table 2), as previously reported by Buiteveld et al. (2007), providing high exclusion probabilities, ranging from 0.973 (VE) to 0.985 (SB) for the RAW data sets, and from 0.983 (VE) to 0.988 (SB) for the MINERROR data sets (Table 3). The high Fis estimates reported by Buiteveld et al. (2007) seem to be dependent on the presence of null alleles at high frequencies (⩾10%) for loci mfc5 and fs 4-46 in Austrian populations and at frequencies around 10% for loci fs 4-46 and fs 1-25 in SB population. Only the inbreeding coefficient of SB (0.083) was significantly different from 0 considering null allele frequencies (Z-test, Z=2.184, P<0.05), whereas the Fis values of the other populations were all below 0.033 and not statistically different from 0 (Table 2).
In the RAW data sets genotyping error rates were between 0.11 (D2) and 0.15 (SB), in line with what found by Oddou-Muratorio et al. (2009) investigating null allele presence on subsets of the SB and VE data presented here. The genotype substitution procedure, but not the binning procedure, markedly decreased the genotyping error rates for some locus–population combinations, simultaneously increasing the EPP. Therefore, MINERROR data sets were obtained by modifying some loci where genotypes were accommodated to take into account null alleles: mfc5 for D1, fs 4-46 for D2, fs 4-46 and fs 1-25 for VE, and fs 1-25 for SB. In D1 the genotyping error decreased from 0.15 to 0.11 from the RAW to the MINERROR data set; in D2 the decrease was from 0.11 to 0.04, from 0.11 to 0.03 in VE and from 0.15 to 0.02 in the SB data sets (Table 3).
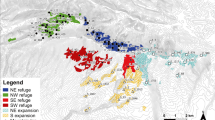
In the maximum likelihood paternity analyses performed on the four MINERROR data sets, we reached high confidence in paternity assignment. Considering as resolved paternities both seeds unequivocally assigned to one local father and seeds pollinated by external trees, the proportion of resolved paternities over the total number of seeds was high in all plots, ranging from 89% in VE to 98% in D2. For 6% of the analysed seeds it was not possible to resolve paternity because two (or more) most likely pollen donors with the same LOD score were found (Table 4). Pollen-mediate gene flow from outside the plot, calculated as the proportion of seeds pollinated by external trees, was high in D1 (0.80), D2 (0.77) and VE (0.75), whereas it was notably lower in SB (0.53) (Figure 2 and Table 4). Self-pollination events are highly infrequent, with only three cases among the 274 local pollination events detected in all plots (1.1%), among which two were in SB. Type-I error estimated by following the simulation method implemented in FaMoz appeared to be higher in the Austrian plots (0.32 in D1 and 0.33 in D2) than in the French ones (0.13 in SB and 0.19 in VE). Type-II error ranged between 0.23 in D1 and 0.35 in VE. It should be kept in mind that type-I and type-II errors are very likely to be often under- and over-estimated, respectively, in real populations when assessed by simulations, and that the effects of the two types of errors compensate each other when gene flow rates are determined (Oddou-Muratorio et al., 2003).
The mating model paternity analysis confirmed what was found by the maximum likelihood method (Figure 2). Only in SB was a lower pollen immigration (0.51±0.07 s.e.) detected, whereas the other three stands were characterized by high gene flow (0.77±0.06 in D1; 0.78±0.05 in D2; 0.81±0.04 in VE). In general, this analysis showed extremely low self-pollination rates in the investigated stands, except D2, where a higher proportion of self-pollinated progenies was detected (0.09±0.02 s.e.). Selection gradients were not included in the final model because (i) the s.e.s of the γ parameters were extremely large and (ii) the final log-likelihood of the two nested models (with and without selection gradients) did not differ significantly (likelihood ratio test: χ2D1=3.88, df=3, P=0.27; χ2D2=0.22, df=3, P=0.97).
Mean pollen dispersal distances greater than 80 m were detected by the maximum likelihood paternity analysis performed on natural stands (80 m±43.34 s.d. in D1 and 81.01±48.70 s.d. in SB), whereas they were 42.32 m (±26.15 s.d.) and 58.71 m (±51.44 s.d.) in D2 and VE, respectively. Maximum dispersal distances detected ranged between 102.98 m in D2 to 210.51 m in SB. The distributions of pollen dispersal distances in D2 and VE were significantly lower than the expected distributions considering the distances among all possible pollen donors and maternal trees (Kolmogorov–Smirnov test: D=0.23, P<0.01 in D2; D=0.27, P<0.001 in VE). On the contrary, in both natural stands (D1 and SB) the two distributions were not statistically different (Figure 3). Dispersal model fitting from NM+ analyses showed that the Weibull kernel was the most likely in D1 and SB, whereas the exponential power kernel fitted better in D2 and VE. Although the shape parameters (b) of the two kernels are not directly comparable, in both kernels b=1 is generally considered as the threshold to distinguish between thin-tailed (b>1) and fat-tailed (b<1) distributions (Austerlitz et al., 2004). Only for SB we found a scale parameter lower than 1 (bp=0.83), although its confidence interval overlaps 1. The estimates of location parameters confirmed what was found in maximum likelihood paternity analyses: the average distance of pollen dispersal (δp) was high for natural stands D1 (184.14 m±105.95 s.e.) and SB (165.99 m±59.64 s.e.), and was shorter for D2 and VE (23.63 m±3.38 s.e. and 60.01 m±21.47 s.e., respectively; Table 5).
Individual male reproductive success, measured as the number of gametes assigned to each pollen donor, was more evenly distributed in the two natural stands, D1 (mean=0.3±0.54 s.d., max=2.5) and SB (mean=0.32±0.6 s.d., max=3), whereas it was more skewed in D2 (mean=0.26±0.76 s.d., max=9) and VE (mean=0.7±1.25 s.d., max=6) (Figure 4). The proportion of pollen contributors, calculated as the number of trees that fathered at least one sampled seed divided by the number of potential pollen donors, ranged between 0.21 in D2 and 0.38 in VE (with 0.30 in D1 and 0.28 in SB). Several variables were tested for their ability to predict the female-specific male reproductive success in the two Austrian plots: distance; phenological overlap; relative position (measured as angles with respect to North, East, South and West) and three different measures of tree sizes, DBH, height and crown area. Quadratic terms and interactions were also tested. None of them, except distance, was significantly related to male female-specific success (slope of success versus distance=−0.005, s.e.=0.0025, with P<0.05 of being equal to 0, analysis of deviance, P<0.05). Total male success was also tested against several predictors: DBH, phenology, height, crown area and the number of ‘nearby maternal trees’. Again morphological and phenological variables were not significantly related with total male success. Only the number of available maternal trees was related significantly with the total male reproductive success by using both deviance analysis (P<0.01) and t-test on the slope (P<0.01). The slope of this relationship was highest for the circle with the shortest radius (10 m) and decreased with increasing radius (Figure 5).
Distribution of male individual reproductive success, measured as the number of pollination events in which every adult tree was involved, for the four study plots. Each black bar represents an adult tree involved in at least one pollination event. The number of adult trees with no paternity assigned is reported near each bar-plot in italic.
Discussion
We analysed pollen flow patterns in four beech stands that differ considerably in their management histories. To overcome methodological uncertainties related to different gene flow pattern analyses, we used two different approaches among the most common in dispersal studies on plants (Gerber et al., 2000; Burczyk et al., 2002; Bacles et al., 2006). In both approaches we employed recently developed techniques to take into account and correct possible genotyping errors that can inflate gene flow rates (Bacles and Ennos, 2008; Chybicki and Burczyk, 2010a). The two methods provided almost identical estimates of gene flow rates. Although our estimates are based on four simple sequence repeat (SSR) markers, and a higher number of markers is usually recommended to improve the precision of paternity inference, we obtained sufficiently high exclusion probabilities (∼0.98) that were further improved by the genotype substitution procedure applied to raw data sets before performing maximum likelihood paternity analysis. Gene flow parameters from the mating model approach were estimated with high precision, with s.e.s comparable to what was found in similar studies based on larger marker sets (for example, Oddou-Muratorio et al., 2010).
Although European beech has a widespread distribution and great economic importance, within-population patterns of gene flow and long-distance dispersal capabilities through pollen have been poorly studied in this species. Aerobiological studies showed its large potential for gene flow through pollen. In fact, there is evidence that meso-scale dispersal capabilities of European beech can be large enough to cover distances up to 1000 km, from Northern Italy to Catalonia (Spain) or across the Mediterranean Sea, from Spain to Tunisia (Teissier du Cros et al., 1981; Belmonte et al., 2008). In bio-geographical studies of European beech, the low genetic differentiation among populations is also usually attributed to its high pollen dispersal capability (Comps et al., 2001; Buiteveld et al., 2007). We found that all populations, with the exception of SB, experienced high pollen flow rates (from 0.75 to 0.81). Our estimates are in agreement with what found recently by Oddou-Muratorio et al. (2010) in a parentage analysis of three beech stands from Mt Ventoux. Nevertheless, parentage and paternity analyses provide estimates of pollen dispersal that are inherently different. Studying pollen movements by parentage analysis (that is, analysing the genetic relationship between seedlings and both potential parent trees) has the limitation of linking pollen fate to the seed dispersal process. This is expected to bias inference on pollen dispersal component. In fact, many successful pollination events will be missed because the vast majority of seeds do not germinate or fail to establish, or simply because seed can move outside the studied area. Oddou-Muratorio et al. (2010), by using NM+ to perform mating model parentage analysis of beech seedlings, found that pollen immigration ranges between 63 and 72% (63 and 68% in two stands inside a recolonization area, and 72% in an ancient forest stand). In general, there is a reduction of ∼10% in pollen immigration compared with our findings (see Table 5). Although comparing results from different studies can be hazardous, our stand at Mt Ventoux is geographically close and ecologically similar to the recolonization plots (FS1 and FS2) studied by Oddou-Muratorio et al. (2010). Our mp estimate in VE is significantly higher than the estimates in these plots as compared by Z-test (VE versus FS1: Z=3.16, P<0.001; VE versus FS2: Z=2.28, P<0.05). Therefore, it can be hypothesized that the reduction of pollen-mediated gene flow from paternity analysis (performed on non-dispersed seeds) to parentage analysis (on seedlings) might result from a slight advantage in the seedling establishment of offspring from local adults in the colonization process. In the same way Bacles and Ennos (2008) detected a limitation in the recruitment of genes carried by immigrant pollen by comparing gene flow rates from non-dispersed seeds and newly established seedlings in fragmented Fraxinus excelsior populations.
High gene flow through pollen seems a general characteristic of Fagaceae. Almost all estimates of pollen immigration in the literature lie between 0.5 and 0.7 (for example, Dow and Ashley, 1998; Streiff et al., 1999; Buiteveld et al., 2001; Valbuena-Carabaña et al., 2005; Chybicki and Burczyk, 2010b). When values lower than 0.5 were found, they were associated with particular ecological conditions. In Quercus semiserrata low pollen immigration was ascribed to high isolation from conspecific populations owing to habitat fragmentation (Pakkad et al., 2008). Similar findings were reported by Pluess et al. (2009) and Hanaoka et al. (2007) in highly disturbed populations of Quercus lobata and Fagus crenata, respectively. Among our studied populations, only SB showed reduced pollen immigration. The study plot is inside a 2000-ha low-altitude (500–1100 m above sea level) beech forest in the St Baume massif, ∼60 km from the nearest beech forest. The persistence of beech at such low altitude is determined by the wet and cool microclimate that characterizes the northern slope of St Baume massif. This forest retained the status of a sacred forest probably since the pre-Roman times and maintained a long history of limited human influence. It presents a markedly archaic character and is considered as a Pre-boreal–Boreal outpost of an early spread from the pleniglacial refugium near the Rhone delta (Delhon and Thiébault, 2005). There is indeed evidence that this population has peculiar phenotypic and genetic characteristics (Delhon and Thiebault, 2005; Buiteveld et al., 2007). Its lower than average pollen immigration and high Fis, coupled with a low self-pollination rate, can therefore represent the consequences of bi-parental inbreeding due to elevated isolation from surrounding genetically distinct populations and the high adult tree density characterizing this stand (150 trees per hectare). Tree density can have significant influences on pollen movements (Hardy, 2009), as discussed in following paragraphs. Significant levels of bi-parental inbreeding were already documented in two managed (at different degree of intensity) beech stands: one in a continuous and one in a fragmented landscape (Chybicki et al., 2009). In particular, these authors demonstrated that bi-parental inbreeding accounted for the majority of homozygous excess in the ‘fragmented’ population.
We found that the average within-population pollination distances of the natural stands D1 and SB were extremely similar, either estimated with FaMoz (80 and 81 m, respectively) or with NM+ (184 and 166 m, respectively). These values are higher than previous estimates for beech based on parentage methods: 30–43 m in three stands studied by Wang (2004) and 28–55 m in three stands studied by Oddou-Muratorio et al. (2010). The majority of the studied stands are not undisturbed, as D1 and SB, but fragmented or located in recolonization areas. Previous estimates of average pollination distances for beech are more similar to what found in our more disturbed plots (D2 and VE), ranging from 24 to 60 m depending on the estimation method. In addition, in D2 and VE pollen dispersal distances are shorter on average than the random sampling of distances calculated from the location of all adult trees. In Fagaceae average pollination distances usually span from a few meters to a maximum of 270 m in Quercus pyrenaica (Valbuena-Carabaña et al., 2005), and our results confirm that F. sylvatica does not represent an exception when within-population spatial processes are considered. However, from an evolutionary point of view, local patterns are of little interest in species that show such an extended long-distance dispersal component of gene flow through pollen, with more than 75% pollination events involving trees outside the study area. Few attempts to include immigration events in the description of propagule dispersal distributions have been made. In all cases it has been shown how the peak, as well as the fatness of the tail of the curve, are usually heavily underestimated (Jones et al., 2005; Piotti et al., 2009). Chybicki and Burczyk (2010b) recently found that, taking into account immigrant pollen, and thus considering the whole pollination process (pollen movements within population and from outside), resulted in an increase of average pollination distances by more than one order of magnitude (29–463 m and 17–297 m in two oak populations characterized by ∼60% pollen immigration).
As far as we know, our study is the first attempt to compare gene flow through pollen between managed and unmanaged forest tree stands by means of paternity analysis, an approach that allows comparing pollen immigration levels, as well as the distributions of pollen dispersal distances and male reproductive success. Finkeldey and Ziehe (2004), in a review of the genetic implications of silvicultural regimes, noticed that genetic structure differences in managed versus unmanaged forests are difficult to monitor because of life-cycle characteristics of most forest tree species. This usually determines a time lag before the consequences of disturbances, such as habitat fragmentation or exploitation, can be detected (Kramer et al., 2008). In fact, several studies did not find any reduction in genetic diversity or changes in the mating systems of wind-pollinated temperate species following silvicultural practices (for example, Rajora and Pluhar, 2003; Robledo-Arnuncio et al., 2004). However, evidence that silvicultural treatments may modify within-stand genetic structure exists (Rajora, 1999; Rajora et al., 2000). Takahashi et al. (2000), comparing primary and recently harvested F. crenata stands, found signs of forest cutting on genetic structure, as less genetic diversity and a considerably higher spatial genetic structure was found in the harvested stand. In a previous work on the effects of management history on genetic diversity in beech stands, Buiteveld et al. (2007) found that pairwise comparisons between managed and unmanaged stands revealed no differences in genetic diversity estimates. On the other hand, they pointed out that long life-span and generation time of beech should be taken into account because the time span during which forest management was practiced in these stands was relatively short (at most two to three generations) and the impact of management may still be manifested after more generations. Therefore, contemporary pattern of gene flow can be a more reliable indicator for studying the consequences of processes that often concern a few recent generations, such as forest management or fragmentation (Aguilar et al., 2008; Piotti, 2009).
To study the possible effect of forest management on pollen flow patterns, we concentrated our attention on D1–D2 comparison. D1 was never managed whereas D2, only 500 m away, was managed according to the shelterwood system (high forest) in combination with natural regeneration. These two stands are characterized by similar pollen flow from outside; mean pollination distance in D1 is approximately twice that in D2 (although D1 is twice the size of D2) and the distributions of male reproductive success are not statistically different. The only detected difference is that pollen dispersal distances in D2 are ‘shorter’ compared with the expected distribution of distances among all potential pollen donors and maternal trees, whereas in D1 the observed and expected distributions are similar. The shelterwood system applied in D2, oriented to maintain a density close to 120 trees per hectare, has determined a marked difference in stand density from D1 old growth forest: adult tree density is 57 trees per hectare in D1, about one-third of the D2 density (163 trees per hectare) (Kramer, 2004). The impact of forest management is often measured in terms of change in stand density. Several silvicultural techniques tend to reduce stand density, increasing inter-individual distances. In some studies, this has been advocated as the cause of enhanced pollen movement in managed populations (El-Kassaby and Jaquish, 1996; Robledo-Arnuncio et al., 2004). Hardy (2009) described how density can mostly affect dispersal by modifying animal behaviour or altering wind movements. He pointed out that in wind-pollinated species plant density can affect wind patterns and the aerodynamic properties of pollen dispersal, and open forest often promotes further-ranging dispersal. The mean effective pollen dispersal distance is therefore expected to be lower under high density and/or when individuals are aggregated, and this might explain the reduced pollen dispersal found in the managed D2 stand.
The results from Austrian stands were also used to study the relationship between reproductive success and phenotypic traits. The mother–father distance seems to be the only determinant factor in shaping the distribution of reproductive success, as we found a weak but significant negative relationship between them. This means that, the higher the availability of ‘pollen traps’ (sampled maternal trees) around a pollen donor, the higher the probability of detecting successful pollinations. Such a finding can have consequences in the experimental planning of future pollen flow studies, but is not directly related to the ability of particular phenotypes to be favoured in the ‘struggle for pollination’. However, neither tree size nor phenological behaviour is related to the number of pollination events recorded for each adult tree in these stands. It is difficult to find a general trend on this relationship in the literature. Hanaoka et al. (2007) found in a small and isolated population of F. crenata that mating frequency was weakly and negatively correlated with mother–father distance, confirming our findings about the importance of seed trap position in the sampling area, and its positive correlation with father stem diameter. In the same species, Asuka et al. (2005), only in one out of the two study plots, found that larger adults had larger number of offspring. In F. sylvatica, the effect of diameter on male and female fertility was studied by Oddou-Muratorio et al. (2010), pointing out how tree size affected both, but with a more pronounced effect on female fertility.
In conclusion, our paternity analyses confirm that, in general, pollen-mediated gene flow in European beech is very high. Forest management by following the shelterwood system has minor influence on within-stand dispersal, and did not change the foreign pollen arrival rate. This can represent a major explanation for previous findings on the low impact of different management strategies on the genetic diversity of this species (Leonardi and Menozzi, 1996; Buiteveld et al., 2007). Population isolation seems to be a more effective factor in reducing genetic connectivity, even if in the plot within the large isolated remnant of St Baume Mountain a pollen flow rate as high as 0.5 was detected. At present, beech range is shrinking in the Mediterranean regions because of climate change and human land use, and several highly fragmented populations can be found in this area (Jump and Penuelas, 2006). A further northward shift of the rear edge of the distribution caused by loss of suitable habitats is predicted in the near future in a recent modelling study (Kramer et al., 2010). In this scenario, information on the relationship between pollen-mediated gene flow and isolation is essential to study the effects of fragmentation on the genetic diversity of tree populations and for planning conservation strategies in temperate anemophilous trees.
Data archiving
Genetic and phenotipic data have been deposited at Dryad (doi:10.5061/dryad.6kt34).
References
Adams WT, Birkes DS (1991). Estimating mating patterns in forest tree populations. In Fineschi S et al. (eds). Biochemical Markers in the Population Genetics of Forest Trees. SPB Academic Publishing: The Hague. pp 157–172.
Aguilar R, Quesada M, Ashworth L, Herrerias-Diego Y, Lobo J (2008). Genetic consequences of habitat fragmentation in plant populations: susceptible signals in plant traits and methodological approaches. Mol Ecol 17: 5177–5188.
Asuka Y, Tomaru N, Munehara Y, Tani N, Tsumura Y, Yamamoto S (2005). Half-sib family structure of Fagus crenata saplings in an old-growth beech-dwarf bamboo forest. Mol Ecol 14: 2565–2575.
Austerlitz F, Dick CW, Dutech C, Klein EK, Oddou-Muratorio S, Smouse PE et al. (2004). Using genetic markers to estimate the pollen dispersal curve. Mol Ecol 13: 937–954.
Bacles CFE, Lowe AJ, Ennos RA (2006). Effective seed dispersal across a fragmented landscape. Science 311: 628.
Bacles CFE, Ennos RA (2008). Paternity analysis of pollen-mediated gene flow for Fraxinus excelsior L. in a chronically fragmented landscape. Heredity 101: 368–380.
Becker M (1981). Taxonomie et caractères botanique. In: Teissier du Cros E et al. (eds). Le Hêtre. INRA: Paris. pp 35–46.
Belmonte J, Alarcón M, Avila A, Scialabba E, Pino D (2008). Long-range transport of beech (Fagus sylvatica L.) pollen to Catalonia (north-eastern Spain). Int J Biometeorol 52: 675–687.
Buiteveld J, Bakker EG, Bovenschen J, de Vries SMG (2001). Paternity analysis in a seed orchard of Quercus robur L. and estimation of the amount of background pollination using microsatellite markers. Forest Genet 8: 331–337.
Buiteveld J, Vendramin GG, Leonardi S, Kramer K, Geburek T (2007). Genetic diversity and differentiation in European beech (Fagus sylvatica L.) stands varying in management history. Forest Ecol Manag 247: 98–106.
Burczyk J, Adams WT, Shimizu JY (1996). Mating patterns and pollen dispersal in a natural knobcone pine (Pinus attenuata Lemmon.) stand. Heredity 77: 251–260.
Burczyk J, Adams WT, Moran GF, Griffin AR (2002). Complex patterns of mating revealed in a Eucalyptus regnans seed orchard using allozyme markers and the neighbourhood model. Mol Ecol 11: 2379–2391.
Burczyk J, Chybicki IJ (2004). Cautions on direct gene flow estimation in plant populations. Evolution 58: 956–963.
Chybicki IJ, Burczyk J (2009a). Simultaneous estimation of null alleles and inbreeding coefficients. J Hered 100: 106–133.
Chybicki IJ, Burczyk J (2009b). NM+: the Software Implementing Parentage-Based Methods for Estimation of Gene Dispersal and Mating Patterns Based on Half-sib Seeds or Seedlings Data. The User Manual. Kazimierz Wielki University: Bydgoszcz, Poland.
Chybicki IJ, Trojankiewicz M, Oleksa A, Dzialuk A, Burczyk J (2009). Isolation-by-distance within naturally established populations of European beech (Fagus sylvatica). Botany 87: 791–798.
Chybicki IJ, Burczyk J (2010a). NM+: software implementing parentage-based models for estimating gene dispersal and mating patterns in plants. Mol Ecol Res 10: 1071–1075.
Chybicki IJ, Burczyk J (2010b). Realized gene flow within mixed stands of Quercus robur L. and Q. petraea (Matt.) L. revealed at the stage of naturally established seedling. Mol Ecol 19: 2137–2151.
Comps B, Gömöry D, Letouzey J, Thiébaut B, Petit RJ (2001). Diverging trends between heterozygosity and allelic richness during postglacial colonization in the European beech. Genetics 157: 389–397.
Crawley MJ (2002). Statistical Computing: an Introduction to Data Analysis Using S-Plus. John Wiley and Sons: New York.
Delhon C, Thiébault S (2005). The migration of beech (Fagus sylvatica L.) up the Rhone: the Mediterranean history of a “mountain” species. Veget Hist Archaeobot 14: 119–132.
Dow BD, Ashley MV (1998). High levels of gene flow in Bur oak revealed by paternity analysis using microsatellites. J Hered 89: 62–70.
Eckert CG, Samis KE, Lougheed SC (2008). Genetic variation across species' geographical ranges: the central–marginal hypothesis and beyond. Mol Ecol 17: 1170–1188.
El-Kassaby YA, Jaquish B (1996). Population density and mating pattern in western larch. J Hered 87: 438–443.
El-Kassaby YA, Benowicz A (2000). Effects of commercial thinning on genetic, plant species and structural diversity in second growth Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) stands. Forest Genet 7: 193–203.
Finkeldey R, Ziehe M (2004). Genetic implications of silvicultural regimes. Forest Ecol Manag 197: 231–244.
Gerber S, Mariette S, Streiff R, Bodénès C, Kremer A (2000). Comparison of microsatellites and amplified fragment length polymorphism markers for parentage analysis. Mol Ecol 9: 1037–1048.
Gerber S, Chabrier P, Kremer A (2003). FAMOZ: a software for parentage analysis using dominant, codominant and uniparentally inherited markers. Mol Ecol Notes 3: 479–481.
Hanaoka S, Yuzurihara J, Asuka Y, Tomaru N, Tsumura Y, Kakubari Y et al. (2007). Pollen-mediated gene flow in a small, fragmented natural population of Fagus crenata. Can J Bot 85: 404–413.
Hardy OJ (2009). How fat is the tail? Heredity 103: 437–438.
Hoebee SE, Arnold M, Duggelin C, Gugerli F, Brodbeck S, Rotach P et al. (2007). Mating patterns and contemporary gene flow by pollen in a large continuous and a small isolated population of the scattered forest tree Sorbus torminalis. Heredity 99: 47–55.
Jones AG, Ardren WR (2003). Methods of parentage analysis in natural populations. Mol Ecol 12: 2511–2523.
Jones AG, Small CM, Paczolt KA, Ratterman NL (2010). A practical guide to methods of parentage analysis. Mol Ecol Res 10: 6–30.
Jones FA, Chen J, Weng GJ, Hubbell SP (2005). A genetic evaluation of seed dispersal in the neotropical tree Jacaranda copaia (Bignoniaceae). Am Nat 166: 543–555.
Jump AS, Peñuelas J (2005). Running to stand still: adaptation and the response of plants to rapid climate change. Ecol Lett 8: 1010–1020.
Jump AS, Peñuelas J (2006). Genetic effects of chronic habitat fragmentation in a wind-pollinated tree. Proc Natl Acad Sci USA 103: 4–8.
Kramer AT, Ison JL, Ashley MV, Howe HF (2008). The paradox of forest fragmentation genetics. Cons Biol 22: 878–885.
Kramer K (2004). Effects of silvicultural regimes on dynamics of genetic and ecological diversity of European beech forests. Impact assessment and recommendations for sustainable forestry Wageningen. Final Report of 5th framework project DynaBeech, QLK5-CT-1999-1210.
Kramer K, Degen B, Buschbom J, Hickler T, Thuiller W, Sykes MT et al. (2010). Modelling exploration of the future of European beech (Fagus sylvatica L.) under climate change—range, abundance, genetic diversity and adaptive response. Forest Ecol Manag 259: 2213–2222.
Leonardi S, Menozzi P (1996). Spatial structure of genetic variability in natural strands of Fagus sylvatica L. (beech) in Italy. Heredity 77: 359–368.
Malaisse F (1967). Contribution à l'étude des hêtraies d'Europe occidentale Note 6. Aperçu climatologique et phénologique relatif aux hêtraies situées l'axe Ardennes belges—Provence. Congrès IUFRO Munich, Exposé II. Section 21 21, pp 325–334.
McCullagh P, Nelder JA (1989). Generalized Linear Models 2nd edn. Chapman Hall: London.
Oddou-Muratorio S, Houot M-L, Demesure-Musch B, Austerlitz F (2003). Pollen flow in the wildservice tree, Sorbus torminalis (L.) Crantz. I. Evaluating the paternity analysis procedure in continuous populations. Mol Ecol 12: 3427–3439.
Oddou-Muratorio S, Vendramin GG, Buiteveld J, Fady B (2009). Population estimators or progeny tests: what is the best method to assess null allele frequencies at SSR loci? Cons Genet 10: 1343–1347.
Oddou-Muratorio S, Bontemps A, Klein EK, Chybicki I, Vendramin GG, Suyama Y (2010). Comparison of direct and indirect genetic methods for estimating seed and pollen dispersal in Fagus sylvatica and Fagus crenata. Forest Ecol Manag 259: 2151–2159.
Pakkad G, Ueno S, Yoshimaru H (2008). Gene flow pattern and mating system in a small population of Quercus semiserrata Roxb. (Fagaceae). Forest Ecol Manag 255: 3819–3826.
Pastorelli R, Smulders MJM, Van't Westende WPC, Vosman B, Giannini R, Vettori C et al. (2003). Characterization of microsatellite markers in Fagus sylvatica L. and Fagus orientalis Lipsky. Mol Ecol Notes 3: 76–78.
Piotti A (2009). The genetic consequences of habitat fragmentation: the case of forests. iForest 2: 75–76.
Piotti A, Leonardi S, Piovani P, Scalfi M, Menozzi P (2009). Spruce colonization at treeline: where do those seeds come from? Heredity 103: 136–145.
Pluess AR, Sork VL, Dolan B, Davis FW, Grivet D, Merg K et al. (2009). Short distance pollen movement in a wind-pollinated tree, Quercus lobata (Fagaceae). Forest Ecol Manag 258: 735–744.
R Development Core Team (2010). R: a Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria. ISBN 3-900051-07-0, URLhttp://www.R-project.org/.
Rajora OP (1999). Genetic biodiversity impacts of silvicultural practices and phenotypic selection in white spruce. Theor Appl Genet 99: 954–961.
Rajora OP, Rahman MH, Buchert GP, Dancik BP (2000). Microsatellite DNA analysis of genetic effects of harvesting in old-growth eastern white pine (Pinus strobus) in Ontario, Canada. Mol Ecol 9: 339–348.
Rajora OP, Pluhar SA (2003). Genetic diversity impacts of forest fires, forest harvesting, and alternative reforestation practices in black spruce (Picea mariana). Theor Appl Genet 106: 1203–1212.
Robledo-Arnuncio JJ, Smouse PE, Gil L, Alia R (2004). Pollen movement under alternative silvicultural practices in native populations of Scots pine (Pinus sylvestris L.) in central Spain. Forest Ecol Manag 197: 245–255.
Robledo-Arnuncio JJ, Gil L (2005). Patterns of pollen dispersal in a small population of Pinus sylvestris L. revealed by total-exclusion paternity analysis. Heredity 94: 13–22.
Scalfi M, Troggio M, Piovani P, Leonardi S, Magnaschi G, Vendramin GG et al. (2004). A RAPD, AFLP and SSR linkage map, and QTL analysis in European beech (Fagus sylvatica L.). Theor Appl Genet 108: 433–441.
Slavov GT, Howe GT, Gyaourova AV, Birkes DS, Adams WT (2005). Estimating pollen flow using SSR markers and paternity exclusion: accounting for mistyping. Mol Ecol 14: 3109–3121.
Slavov GT, Leonardi S, Burczyk J, Adams WT, Strauss SH, DiFazio SP (2009). Extensive pollen flow in two ecologically contrasting populations of Populus trichocarpa. Mol Ecol 18: 357–373.
Sokal RR, Rohlf FJ (1995). Biometry: Principles and Practices of Statistics in Biological Research 3rd edn. W.H. Freeman and Company: New York.
Streiff R, Ducousso A, Lexer C, Steinkellner H, Gloessl J, Kremer A (1999). Pollen dispersal inferred from paternity analysis in a mixed oak stand of Quercus robur L. and Q. petraea (Matt.) Liebl. Mol Ecol 8: 831–841.
Takahashi M, Mukouda M, Koono K (2000). Differences in genetic structure between two Japanese beech (Fagus crenata Blume) stands. Heredity 84: 103–115.
Tanaka K, Tsumura Y, Nakamura T (1999). Development and polymorphism of microsatellite markers for Fagus crenata and the closely related species, F. japonica. Theor Appl Genet 99: 11–15.
Teissier du Cros E, Le Tacon F, Nepveu G, Pardé J, Timbal JE (1981). Le Hêtre. Département des Recherches Forestières, INRA: Paris.
Valbuena-Carabaña M, Gonzalez-Martinez SC, Sork VL, Collada C, Soto A, Goicoechea PG et al. (2005). Gene flow and hybridisation in a mixed oak forest (Quercus pyrenaica Willd. and Quercus petraea (Matts.) Liebl.) in central Spain. Heredity 95: 457–465.
Wang KS (2004). Gene flow in European beech (Fagus sylvatica L.). Genetica 122: 105–113.
Williams CG (2010). Long-distance pine pollen still germinates after meso-scale dispersal. Am J Bot 97: 846–855.
Acknowledgements
This study was financially supported by the European Commission through the Dynabeech project (5th Framework Programme, QLRT-1999-01210). The support to KK from the project Genetic adaptation of plant species to climate change at the limits of their areas (KB-14-004-004), funded by the Dutch Ministry of Economics, Agriculture and Innovation, is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
About this article
Cite this article
Piotti, A., Leonardi, S., Buiteveld, J. et al. Comparison of pollen gene flow among four European beech (Fagus sylvatica L.) populations characterized by different management regimes. Heredity 108, 322–331 (2012). https://doi.org/10.1038/hdy.2011.77
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2011.77
Keywords
This article is cited by
-
Genetic variation and signatures of natural selection in populations of European beech (Fagus sylvatica L.) along precipitation gradients
Tree Genetics & Genomes (2018)
-
Comparison and confirmation of SNP-bud burst associations in European beech populations in Germany
Tree Genetics & Genomes (2017)
-
Exploring and conserving a “microcosm”: whole-population genetic characterization within a refugial area of the endemic, relict conifer Picea omorika
Conservation Genetics (2017)
-
Relationships between population density, fine-scale genetic structure, mating system and pollen dispersal in a timber tree from African rainforests
Heredity (2016)
-
Development and Characterization of Three Highly Informative EST-SSR Multiplexes for Pinus halepensis mill. and their Transferability to Other Mediterranean Pines
Plant Molecular Biology Reporter (2016)