Introduction

Intraocular pressure (IOP) greater than 21 mm Hg, commonly classified as ocular hypertension (OHT),1 substantially increases the risk of glaucoma.2 Glaucoma, a neurodegenerative disease of the retinal ganglion cells, is the second leading cause of blindness worldwide.3 In the United States, 4 million people have glaucoma and 130 000 are legally blind from the disease.3 In the Australian Blue Mountains Eye study of adults 49 years of age and older, the prevalence of open-angle glaucoma was 3% and OHT was found in 3.7% of participants.1 Control of IOP is important in patients with glaucoma:4 a decrease of 1 mm Hg may lead to a 10% reduction in the risk of progressive nerve damage.5, 6 Reduction and control of IOP are the only effective treatments for glaucoma.

IOP is measured by eye-care professionals to screen for, diagnose, treat and monitor OHT and eye diseases such as glaucoma. The Goldmann applanation tonometer in experienced hands is recognised as the gold standard for IOP measurements.7 Both Goldmann applanation and non-contact tonometers are known to produce clinically significant systematic errors if inadequately maintained and calibrated,8, 9, 10, 11, 12, 13, 14, 15 and current calibration intervals may be too long.8, 9, 12, 14, 16, 17, 18

Systematic errors in IOP measurements are likely to lead to over- or under-detection of OHT. Over-detection of OHT during screening may result in excessive referrals to ophthalmologists, while under-detection may place individuals at increased risk of glaucoma. Inadequate calibration or variability of calibration19 of tonometers used for treating or monitoring patients with OHT or glaucoma may cause apparently random variations in IOP, even if monitoring is performed on a single tonometer.

The effects of systematic errors in IOP measurements on over- and under-detection of OHT and treatment of glaucoma are not known and have not been studied. There is no published quantitative evidence indicating how accurate tonometers should be. In this study, we analysed IOP measurements from a population study to estimate the sensitivity of detection of OHT to systematic errors in IOP measurements.

Materials and methods

We analysed valid IOP measurements obtained in the Blue Mountain Eye Study (BMES).1 The BMES was approved by the Western Sydney Area Health Service Human Ethics Committee, and written, informed consent was obtained from all participants. All IOP measurements were performed using a single Goldmann applanation tonometer and slit lamp (both Haag-Streit, Bern, Switzerland) after a drop of Fluress (benoxinate hydrochloride 0.4%, sodium fluorescein 0.25%, Barnes-Hind, Sunnyvale, CA, USA). A single measurement was taken and repeated if judged unreliable. All IOP measurements were performed by the same operator (a trained study orthoptist), during the 3-year course of the BMES. Any IOP measurements less than 10 or greater than 21 mm Hg were repeated by the Principal Investigator in the BMES (PM). The tonometer was calibrated regularly (at least 3 times per year during the course of the study).

We analysed all valid left, right and highest IOP measurements from all participants using a method similar to that published earlier for analysing blood pressure distributions.20 IOP measurements were assumed to be rounded to the nearest mm Hg: histograms and cumulative distributions were calculated using thresholds at midpoints between integer IOP values. An inverse cumulative distribution indicating the percentage of subjects with IOPs greater than the abscissa value was calculated by summing the histograms and subtracting the sums from 100. First-, second- and third-order polynomials were fitted to the logarithm of the cumulative distribution by linear regression to smooth the distribution and facilitate interpolation. Goodness of fit of the polynomials was assessed by examining R2, the standard errors of the regressions and the statistical significance of the coefficients. Confidence intervals (95%) around mean predicted values were calculated.21 The proportion of subjects who had OHT (IOP>21 mm Hg) was estimated from the polynomial. To estimate the effects of systematic measurement errors, the proportion was re-estimated assuming the tonometer systematically over- and under-read by 0–4 mm Hg at 0.1 mm Hg intervals. The sensitivity of over- and under-detection of OHT to the cutoff IOP was investigated by repeating the analysis for cutoff IOPs of 20 and 22 mm Hg. Data analysis was performed using Matlab 2009b (Mathworks, Nattick, MA, USA).

Results

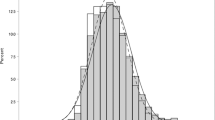
Histograms of right and left IOP measurements are shown in Figure 1. The difference between the IOP of left and right eyes was 0.09 ±1.95 (mean±SD) mm Hg and the Pearson correlation coefficient was 0.78. Results for left, right and highest IOPs were similar, therefore we report results for highest IOPs only. The cumulative distribution indicating the percentage of subjects with highest IOP greater than 17.5–27.5 mm Hg is shown in Figure 2, in which the vertical scale is logarithmic. The SE of the first-, second- and third-order regressions were 0.0900, 0.0219, and 0.0233 logarithmic units, corresponding to 1.230, 1.052, and 1.055 percentage points, respectively. Respective R2 values were 0.975, 0.999, and 0.999. The coefficients of the second-order polynomial were all significantly different from 0 at the 95% level of confidence. Therefore, the relationship between the logarithm of the inverse cumulative distribution and IOP is described best by a second-order polynomial.

Figure 1
figure 1

Histograms of all baseline intraocular pressures measured in the Blue Mountains Eye Study.1

Full size image
Figure 2
figure 2

Inverse cumulative distributions showing proportions (%) of participants with highest IOP greater than the abscissa value. Lines above and below the regression line indicate 95% confidence interval (CI) of predicted mean value. Vertical and horizontal lines indicate percentages of participants (with corresponding 95% CI) in whom ocular hypertension (IOP>21 mm Hg) would be detected when the tonometer has a systematic error of −2, 0, and +2 mm Hg, respectively.

Full size image

Over- and under-detection of OHT (highest IOP>21 mm Hg) caused by systematic errors of ±2 mm Hg are indicated by the construction lines in Figure 2. Changes in the apparent prevalence of OHT that would be caused by systematic errors in IOP measurements of ±1, ±2, ±3 and ±4 mm Hg are shown in Table 1. Figure 3a and b show the effects of systematic errors in IOP on the detection of OHT over the continuous ranges 0 to +4 and −4 to 0 mm Hg, respectively, using cutoff IOPs of 20, 21, and 22 mm Hg.

Table 1 Apparent prevalence (%) of ocular hypertension (highest IOP>21 mm Hg) in the Blue Mountains Eye Study1 associated with systematic errors in IOP measurements
Full size table
Figure 3
figure 3

Over-detection of ocular hypertension caused by positive systematic measurement errors (a), and proportion of individuals with ocular hypertension who would be missed due to negative systematic measurement error (b). The dotted and broken lines indicate the effects of variations in cutoff IOP on over- and under-detection.

Full size image

Discussion

In this study, we show that detection of OHT is very sensitive to systematic errors in IOP measurements. When a population is screened for OHT, a tonometer that over-reads by 1 mm Hg may result in the number of positive results increasing by ∼58% (Figure 3a) or ∼3.3% of the population (Table 1). Conversely, a tonometer that under-reads by 1 mm Hg may result in ∼34% of individuals with OHT (1.9% of the population) being missed (Figure 3b). Systematic errors of +1.5 mm Hg and −1.7 mm Hg may result in the number of individuals with detected OHT doubling or halving, respectively. Larger systematic errors of ±4 mm Hg may result in the number of positive screening results increasing by a factor of seven (Figure 3a), or 76% of individuals with OHT being missed (Figure 3b). Some patients whose IOP is screened with an inadequately calibrated tonometer may be referred to an ophthalmologist unnecessarily and, some patients with OHT may not be referred and be at unnecessarily increased risk of glaucoma.

Figure 3a and b shows that under- and over-detection of OHT does not depend strongly on the IOP cutoff used to define OHT. For example, at a systematic error of +3 mm Hg, a change of cutoff from 21–22 mm Hg changes over-detection from 345 to 293 (Figure 3a), a change of only (293−345)/345×100=−15%. An earlier study that showed when the logarithm of the inverse cumulative distribution is linear, variations in the cutoff have no effect on over- and under-detection.20 The weak non-linearity shown in Figure 2 is associated with small changes in under- and over-detection of OHT with changes in IOP cutoff.

Systematic error or bias may be common in both non-contact and applanation tonometers in regular clinical use. Three non-contact tonometers evaluated against a calibrated Goldmann applanation tonometer exhibited mean errors of 0.5, 2.9, and 1.8 mm Hg after 20, 9, and 24 months of operation, respectively.8 Choudhari et al9 checked the calibration of 132 Goldmann applanation tonometers, using the standard weight bar supplied by the manufacturer, 6 months after they had been calibrated by hospital biomedical engineers, and found calibration errors ranging from −8 to +20 mm Hg. Intra- and inter-observer limits of agreement for duplicate calibrations were up to 4 mm Hg.9 At 20 mm Hg, 55%, 10%, and 5% of tonometers had errors greater than or equal to 2, 4, and 6 mm Hg respectively.9 Only 4% of tonometers complied with the manufacturer’s tolerance of ±0.5 mm Hg. Sandhu et al12 found that 6 months after 34 Goldmann tonometers had been calibrated by a specially designated technician, 41% exhibited calibration errors of 3 mm Hg or greater at a nominal 20 mm Hg. Four months later, 52% exhibited calibration errors of 3 mm Hg or greater.12 George et al22 assessed in vivo agreement between two calibrated Goldmann applanation tonometers from different manufacturers and found limits of agreement of −2.47 to +6.16 mm Hg. Systematic measurement errors may also be caused by distortions of the applanating surface of disposable tonometer heads.23

In a survey of 155 ophthalmology units in the United Kingdom, Kumar et al17 found that 39% of units checked the calibration of their Goldmann tonometers either never or in a random manner. In a separate UK survey of ophthalmology residents, 85% never checked tonometers and 70% felt that calibration checks were not part of their responsibility.16 Only 7% checked the tonometer at the start of each clinical session and 8% would only check the tonometer if they had suspicious or unexpected measurements.16

IOP is not the only variable used by ophthalmologists to estimate risk of loss of vision. Glaucoma occurs in many patients whose IOP is below 21 mm Hg. Clinical optic disc examination and other quantitative measurements24 contribute to the detection, treatment and management of glaucoma. IOP, however, is an important risk factor for glaucoma25 measured to screen for OHT, and it is important that the measurement is reliable.

Intra-individual variation of IOP can be several mm Hg,26, 27 often substantially larger than calibration errors, possibly leading to an assumption that small systematic errors are not important. Systematic errors are approximately constant and create a bias at every IOP reading in every individual. The effect is similar to a shift in the population distribution of IOP. Decisions regarding treatment or follow-up are made, explicitly or implicitly, for every patient examined. On average, over a large number of patients, a small positive systematic error will result in more patients being treated or referred for further investigation, and a small negative systematic error will result in some patients not being treated or referred, who otherwise would be. This study quantifies those effects and shows that the influence of small systematic errors may be surprisingly large.

Important limitations of this study include the intra-individual variability of IOP of the participants and the possibility of undetected calibration errors in the tonometers used in the Blue Mountains Eye Study. Intra-individual variability and random calibration errors would increase the inter-individual IOP variance, broaden the IOP distribution and hence reduce the slope of the inverse cumulative distribution of IOP. This slope reduction would reduce the apparent sensitivity of OHT detection to tonometer calibration errors. Hence, this study may under-estimate the sensitivity.

We conclude that tonometers should be maintained and properly calibrated at intervals short enough to control systematic errors in IOP measurements to substantially less than 1 mm Hg.