Model-Based Multifactor Dimensionality Reduction to detect epistasis for quantitative traits in the presence of error-free and noisy data

Abstract

Detecting gene–gene interactions or epistasis in studies of human complex diseases is a big challenge in the area of epidemiology. To address this problem, several methods have been developed, mainly in the context of data dimensionality reduction. One of these methods, Model-Based Multifactor Dimensionality Reduction, has so far mainly been applied to case–control studies. In this study, we evaluate the power of Model-Based Multifactor Dimensionality Reduction for quantitative traits to detect gene–gene interactions (epistasis) in the presence of error-free and noisy data. Considered sources of error are genotyping errors, missing genotypes, phenotypic mixtures and genetic heterogeneity. Our simulation study encompasses a variety of settings with varying minor allele frequencies and genetic variance for different epistasis models. On each simulated data, we have performed Model-Based Multifactor Dimensionality Reduction in two ways: with and without adjustment for main effects of (known) functional SNPs. In line with binary trait counterparts, our simulations show that the power is lowest in the presence of phenotypic mixtures or genetic heterogeneity compared to scenarios with missing genotypes or genotyping errors. In addition, empirical power estimates reduce even further with main effects corrections, but at the same time, false-positive percentages are reduced as well. In conclusion, phenotypic mixtures and genetic heterogeneity remain challenging for epistasis detection, and careful thought must be given to the way important lower-order effects are accounted for in the analysis.

INTRODUCTION

Understanding the effects of genes on the development of complex diseases and traits in human is a major aim of genetic epidemiology. These kinds of diseases are controlled by complex molecular mechanisms characterized by the joint action of several genes that could have different effect sizes. In this context, traditional methods within a regression paradigm involving single markers have limited use and more advanced and efficient methods are needed to identify gene–gene interactions and epistatic patterns of susceptibility. One of these methods is the Multifactor Dimensionality Reduction (MDR) method,¹ which nicely tackles the dimensionality problem involved in interaction detection by pooling multi-locus genotypes into two groups of risk based on some threshold value. Those cells with a case/control ratio equal to or above the threshold are labeled as High risk and the remaining cells as Low risk. Although MDR has been widely and successfully used for interaction detection (eg, URL: http://compgen.blogspot.com/2006/05/mdr-applications.html), it suffers from ;some major drawbacks, including that important interactions could be missed owing to pooling too many cells together or that proposed MDR analyses will only reveal at most one significant epistasis model, selection being based on computationally demanding cross-validation and permutation strategies. To overcome the aforementioned hurdles, Calle et al^{2, 3} developed Model-Based MDR (MB-MDR) for dichotomous traits and unrelated individuals, hereby providing the basis for a flexible framework to detect gene–gene interactions. The method has been made available via an R package mbmdr. The principal difference between MDR and MB-MDR is that MB-MDR merges multi-locus genotypes exhibiting some significant evidence of High or Low risk, based on association testing or modeling, rather than on comparison with a threshold value. In addition, those multi-locus genotypes that either show no evidence of association or have no sufficient sample size contribute to an additional MB-MDR category, that of ‘No Evidence for risk’. Note that despite the fact that Lou et al⁴ recognized in part the necessity to adjust for covariates and to extend MDR to quantitative traits, issues related to significance assessment remain, as explained in detail by Cattaert et al.⁵

Although a β-version of MB-MDR for quantitative traits has already been applied by Mahachie John et al,⁶ its power under several conditions, including the presence of error sources or noise (eg, genotyping errors, missing genotypes, phenotypic mixtures and genetic heterogeneity (GH)), has never been investigated. The aim of this study is to evaluate the power of MB-MDR for quantitative traits to detect gene–gene interactions, for a variety of simulated scenarios. We will restrict attention to two-order interactions, although MB-MDR can be used to highlight gene–gene interactions of any order.

METHODS

MB-MDR

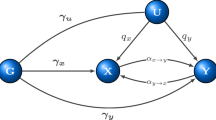
The three steps of the MB-MDR strategy used for this simulation study are summarized below and visualized in Figure 1. For more general details, we refer to Cattaert et al.⁵

Figure 1

Graphical presentation of the key steps involved in MB-MDR analysis.

MB-MDR step 1: multi-locus cell prioritization

For every pair of markers, data are organized in a two-way table, with nine genotype cells. Each two-locus genotype cell, c_j, in such a table, is assigned to one of three risk categories, High risk (H), Low risk (L) or No Evidence for risk (O), as a result of association tests on each of the individual two-locus genotype cells with the response variable Y. Cell-dependent testing for H, L and O labeling is carried out with a Student's t-test, at the liberal significance level of 0.10, as the power to detect association using individual cells is likely to be limited. If for a two-locus cell, the Student's t-test, comparing the cell's mean with the mean of the remaining eight cells, is not significant at 0.10, the cell is labeled as O. The sign of the Student's t-test statistic is used to distinguish between H and L: a positive (negative) sign refers to risk H (L).

MB-MDR step 2: association test on lower-dimensional construct

The result of the first step is thus a new categorical variable X with values H, L and O, which captures information about the importance of the pair of markers with respect to the trait. A new association test is subsequently performed now for the new construct X on Y. In particular, we consider the maximum of W_H and W_L, which are Student's t-tests for comparing H versus {L, O} means and L versus {H, O} means, respectively.

MB-MDR step 3: significance assessment

Once the dimensionality reduction procedure has been implemented and tests for association have been performed, for every pair of markers in the data, a single test result {W_H, W_L} per marker pair is obtained. Because the test statistics are obtained after combining cells according to X, using information about the trait Y, W_H and W_L will no longer be t-distributed. In fact, these tests are expected to generate inflated type I errors. We therefore assess the significance of max {W_H, W_L} per marker pair, by adopting a permutation-based strategy (999 replicates) that corrects for multiple testing (over all marker pairs) and adequately controls family-wise error rate at α=5%. In particular, we implement the step-down maxT-adjusted P-values approach, as outlined by Westfall and Young.⁷

Adjustment for main effects

Some interactions can be identified simply because of highly significant lower-order effects, and are therefore not genuine. That is why we also consider MB-MDR adjusted analyses in the following way: with and without adjustment for main effects of functional SNPs. Main effects are adjusted for in MB-MDR by first regressing them out in a data preparation step and then considering the residuals from the regression model as new traits. Two extreme ways of correcting are considered: the additive model and the co-dominant model. When adjusting for main effects in the presence of GH, we take into account that different functional pairs are relevant for heterogeneous subpopulations.

Data simulation

Each of 500 data sets in a simulation setting consists of 1500 unrelated individuals with 10 SNPs (in linkage equilibrium), two of which are functional. The minor allele frequencies of a non-functional marker SNP_j are fixed at p_j=0.1+(j−3) × 0.05, j=3,…,10, whereas the minor allele frequencies of the functional SNPs (SNP₁, SNP₂) are taken to be equal, and varying as (p₁, p₂)=(p, p), p∈{0.1, 0.25, 0.5}. All SNPs are assumed to be in Hardy–Weinberg Equilibrium.

Two epistasis models that incorporate varying degrees of epistasis are considered: Model 27 and Model 170 of Evans et al,⁸ hereafter referred to as M27 and M170, respectively. To increase the phenotypic mean, M27 requires an individual to have at least one copy of the increaser allele at both loci, whereas M170 requires an individual to be heterozygous at one locus and homozygous at the other. As p increases, the contribution to the total genetic variance of epistasis variance relative to main effects variances increases for M170 (decreases for M27) (Table 1).⁵ The phenotypic means for these epistasis models only take two values, μ_L (Low phenotypic mean) and μ_H (High phenotypic mean). The total phenotypic variance σ_tot², that is, the sum of genetic variance at both loci 2σ₁²=σ_main² (the minor allele frequencies for the functional SNPs are taken to be the same), epistasis variance σ_epi² and environmental variance σ_env², is fixed at 1. As a consequence, the total genetic variance, defined as 2σ₁²+σ_epi², has an interpretation of a broad heritability measure. Throughout this document it will further be referred to as g², to clearly indicate that the interpretation as a heritability is due to the imposed normalization constraints. The parameter g² is varied as g²∈{0.01, 0.02, 0.03, 0.05, 0.1}. Explicit formulae for these variance components can be obtained from Evans et al.⁸

Table 1 Proportion σ²_gen/g² of the total genetic variance in error-free data that is due to genetics in the error-prone data, exhibiting either 5% (GE5) or 10% (GE10) genotyping errors, or 25% (PM25) or 50% (PM50) phenotypic mixture

In addition, 1000 null data sets are generated under the most general null hypothesis of no association between any of the 10 SNPs and the trait (ie, g²=0, no main effects and no epistasis).

Introducing noise

Apart from simulating error-free data, we also simulate different error sources to investigate their impact on the performance of MB-MDR. These involve introducing 5 and 10% missing genotypes (MG5 and MG10), 5 and 10% genotyping error (GE5 and GE10), 25 and 50% phenotypic mixtures (PM25 and PM50) and 50% GH. It is important to realize that the foregoing derivations of variance decomposition relate to a population as whole. When generating sources of error, estimates of variability will no longer tend to the estimates at the population level. In other words, the actual genotypic variance will no longer equal g². Missing genotypes (MG5 and MG10) and genotyping errors (GE5 and GE10) are also introduced in the null data, leading to a total of 255 simulation settings, so as to be able to assess the impact of these on MB-MDR's type I error control in the presence of noise.

In particular, scenarios MG5 and MG10 are generated by selecting genotypes completely at random from the original data and by setting them to missing. This introduces different per-individual and per-SNP percentages of missingness, reducing the effective sample size, yet maintaining the validity of the variance component estimates.

As in Ritchie et al,⁹ genotyping error is simulated using a directed-error model.¹⁰ This model postulates that there is a larger probability for the minor allele to be consistently mis-genotyped (over-represented). In this study, either 5% (GE5) or 10% (GE10) of the available genotypes in the original data set are sampled. From these, homozygous genotypes for the common allele become heterozygous and heterozygous genotypes for the rare allele become homozygous. The effect of adding genotyping errors to the original data is that the actual genetic contribution, σ_gen², to the trait variance is reduced compared to the assumed genetic variance, g², of the simulation setting due to the additional variability (noise) introduced into the system (Table 1).

GH is simulated such that there are actually two different two-locus combinations increasing/decreasing the phenotypic mean. Half of the individuals have one pair of functional SNPs (SNP1 and SNP2), and the other half have the other pair of functional SNPs (SNP3 and SNP4). Introducing the notations G_L (G_H) as the multi-locus genotypes leading to a Low (High) phenotypic mean, traits are simulated according to the distributions specified below:

Minor allele frequencies of all four functional SNPs are taken to be equal, that is, p∈{0.1, 0.25, 0.5}.

Phenotypic mixing in genetics may occur when a percentage of individuals with high phenotypic mean have genotype combinations that are consistent with low phenotypic mean.

In particular, a mixing proportion of w∈[0,1] of phenotypic mixture, trait values are simulated according to

with mixing proportion either 25% (PM25) or 50% (PM50), and π, the probability of a multi-locus genotype giving rise to a high phenotypic mean μ_H.

RESULTS

The impact of not correcting for lower-order effects

Table 2 gives an overview of MB-MDR empirical type I error rates in the absence and presence of noise (MG and GE). We observe that MB-MDR empirical type I error percentages are close to the nominal type I error percentage of 5%, when no correction for main effects is performed. When we adjust for main effects, type I error percentages are further reduced and seem to drop below the theoretical value. Similar trends are observed when genotyping errors and missing genotypes are introduced in the data.

Table 2 Type I error percentages for data generated under the general null hypothesis of no genetic association in the absence and presence of noise

Power estimates of MB-MDR to detect the correct interacting pair, SNP1 × SNP2 (in the absence of GH) from error-free and noisy data are shown in Figure 2. The actual numerical results of the power profiles plotted in Figure 2 are presented in Supplementary Table S1. This table also includes the corresponding empirical power estimates related to main effects adjusted analyses.

Figure 2

Empirical power estimates of MB-MDR as the percentage of analyses where the correct interaction (SNP1 × SNP2) is significant at the 5% level, for error-free and noise-induced simulation settings. Results are shown for MB-MDR analysis without main effects adjustment and simulated scenarios other than GH.

In the absence of any adjustment for lower-order genetic effects (ie, main effects), we notice that power profiles largely follow the same trajectory, except in the presence of 50% phenotypic mixture (PM50). For all scenarios of p, power increases with increasing g² (Figure 2 and Supplementary Table S1). Moreover, the power of MB-MDR (ranging from 54 to 100%, p=0.1, 38–100%, p=0.25, 33–100%, p=0.5 under M170 and from 44 to 100%, p=0.1, 43–100%, p=0.25, 39–100%, p=0.5 under M27 for error-free data; Supplementary Table S1) is hardly affected by introducing small percentages of missing genotypes (MG5 in Figure 2), irrespective of the epistasis model under investigation. Power estimates for MG5 range from 42 to 100%, p=0.1, 33–100%, p=0.25, 28–100%, p=0.5 and from 33 to 100%, p=0.1, 34–100%, p=0.25, 31–100%, p=0.5 under M170 and M27, respectively (Supplementary Table S1). For MG10, power obviously reduces further, but not in a dramatic way compared to MG5: power estimates reduce to a minimum of 31%, p=0.1, 25%, p=0.25, 25%, p=0.5 and to a minimum of 31%, p=0.1, 28%, p=0.25, 22%, p=0.5 for M170 and M27, respectively). When 5% genotyping errors are introduced in the population, systematically lower power curves are obtained than that in the presence of randomly missing genotypes. However, high percentages of genotyping error (GE10) or high percentages of phenotypic mixture (PM50) generally lead to the lowest power performance of MB-MDR (Figure 2). Power estimates in the presence of 10% genotyping errors are in the range of 12–100%, p=0.1, 8–100%, p=0.25, 12–100%, p=0.5 for model M170 and in the range of 9–100%, p=0.1, 20–100%, p=0.25, 26–100%, p=0.5 for model M27 (Supplementary Table S1). High percentages of phenotypic mixture have a negative impact on MB-MDR power, which is also indicated by the minimally observed empirical power estimates for PM50. Power estimates for the latter are in the range of 3–98%, p=0.1, 3–97%, p=0.25, 2–95%, p=0.5 for M170 and in the range of 3–95%, p=0.1, 2–97%, p=0.25, 3–95%, p=0.5 for M27.

Not surprisingly, there is a higher chance of identifying epistasis models for analyses without main effects correction as compared to analyses that do account for lower-order effects. The latter epistasis models usually involve other SNPs pairing with one of the functional SNPs (results not shown) and should therefore be considered as false positives. Empirically estimated false-positive percentages, for a variety of scenarios, excluding GH settings, are reported in Supplementary Table S2 (‘No Correction’ versus ‘Main Effects Correction’ estimates). For error-free data, and no adjustments for main effects, the false-positive percentage of MB-MDR of identifying a significant epistasis model not involving the actual functional pair of SNPs ranges from 28 to 100%, p=0.1, 6–53%, p=0.25, 6–7%, p=0.5 for M170 and from 15 to 99%, p=0.1, 26–100%, p=0.25, 38–100%, p=0.5 for M27. When main effects are accounted for in error-free data, the false-positive percentage ranges from 3 to 39%, p=0.1, 3–12%, p=0.25, 3–6%, p=0.5 under M170 and from 3 to 7%, p=0.1, 3–21%, p=0.25, 2–98%, p=0.5 under M27 (Supplementary Table S2). In general, Supplementary Table S2 shows that irrespective of how the main effects adjustment is performed (using an additive or co-dominant model) and irrespective of the type of noisiness introduced, false-positive percentages are typically lower than their ‘uncorrected’ counterparts.

The impact of appropriately correcting an epistasis analysis for lower-order effects

Profiles for the empirical power estimates of MB-MDR to detect the correct two functional loci from error-free data with (additive and co-dominant) main effects correction and without main effects adjustment are plotted in Figure 3. Here, we observe that the power to identify the correct causal pair is reduced when a main effects correction is performed, with the lowest power levels obtained for co-dominant correction. The discrepancy between additive and co-dominant main effects adjustment is particularly pronounced for M27 and p=0.5. For M170 and p=0.5, the nature of the lower-order effects adjustment has virtually no influence on power. Power profiles for different sources of noise, according to main effects adjustment method, are given in Supplementary Figure S1-i (missing genotypes), Supplementary Figure S1-ii (genotyping errors) and Supplementary Figure S1-iii (phenotypic mixture). The empirical power estimates used to generate Supplementary Figure S1 are also presented in Supplementary Table S1. Here, drawing conclusions is more subtle, although generally speaking, empirical power estimates are smaller with co-dominant correction as opposed to additive correction.

Figure 3

Empirical power estimates of MB-MDR as the percentage of analyses where the correct interaction (SNP1 × SNP2) is significant at the 5% level, for error-free simulation settings. Legend: no main effects adjustment (—), main effects adjustment via additive coding (…) and co-dominant coding (- - -).

Numerical values on the effect of using different main effects adjustments on the false-positive percentage to identify incorrect two-locus models can be derived from Supplementary Table S2. For error-free data, the false-positive percentages after additive main effects correction range from 5 to 39%, p=0.1, 5–12%, p=0.25, 3–6%, p=0.5 for M170 and from 4 to 7%, p=0.1, 4–21%, p=0.25, 9–98%, p=0.5 for M27. Using co-dominant coding to adjust for lower-order effects, the false-positive percentages range from 3 to 6%, p=0.1, 3–4%, p=0.25 or p=0.5 for M170 and from 3 to 6%, p=0.1, 3–3%, p=0.25 and from 2 to 4%, p=0.5 for M27. In fact, the practice of correcting an MB-MDR epistasis analysis using a co-dominant main effects model has the tendency to be over-conservative (Supplementary Table S2).

Genetic heterogeneity

So far, we have not yet discussed the performance of MB-MDR for quantitative traits in the presence of GH. Figure 4 shows empirical power curves to identify true genetic interactions in the presence of GH for a variety of simulation settings. Results are shown for MB-MDR analysis without main effects correction (Figure 4, row 1 for M170 and row 3 for M27) and with main effects correction (additive coding) adjustment (Figure 4, row 2 for M170 and row 4 for M27). As in non-GH settings, power estimates are larger when no correction for main effects is performed than when main effects are accounted for, with generally the most severe power loss observed for co-dominant main effects correction. However, when the contribution of main effects to the total genetic variance is ignored, false-positive percentages rise as well, ranging from 7 to 100% for M27 and from 4 to 97% for M170. When we adjust for main effects (additive coding), power estimates to identify the first pair (SNP1 × SNP2) drop to less than 50% for both M27 and M170, with the exception of M170. For the latter, and a genetic variance of 0.1, MB-MDR power is estimated to be 95 and 92% for p=0.25 and 0.5, respectively. Under a co-dominant correction, power estimates drop to less than 7% for both models, with the exception of p=0.25 or 0.5 and g²=0.05 or 0.1. For the latter, power is estimated to be 15 and 26% for M170 and M27, respectively when p=0.1 and g²=0.1. For M27, power=31%, p=0.25 and g²=0.1. For M170, p=0.25 or 0.5, power estimates are around 30 and 88% for g²=0.05 and 0.1, respectively. Detailed information about empirical power estimates are given in Supplementary Table S6.

Figure 4

Empirical power estimates of MB-MDR as the percentage of analyses where the correct interactions (SNP1 × SNP2) and/or (SNP3 × SNP4) are significant at the 5% level, in the presence of GH. First 2 rows: MB-MDR without and with main effects correction for model M170, respectively. Last 2 rows: MB-MDR without and with main effects correction for model M27, respectively. Main effects are corrected for via additive coding. Different definitions for power are adopted: power to identify both interacting pairs SNP1 × SNP2 and SNP3 × SNP4 (cyan); power to identify SNP1 × SNP2 (black); power to identify SNP3 × SNP4 (magenta), power to identify at least one of the interactive pairs (coral).

DISCUSSION

Understanding the effects of genes on the development of complex diseases is a major aim of genetic epidemiology. Several studies have indicated that MDR has good power to identify gene–gene interactions in both simulated and real-life data.⁹ Although MB-MDR has profiled itself as a promising extension of MDR accommodating study designs that are more complex than unrelated case–control settings,^{2, 3, 5, 6} a thorough investigation of its full potential, under a variety of real-life distorting factors, such as missing genotypes, genotyping errors, phenotypic mixtures and last but not least GH, has never been carried out in the context of quantitative traits. This study has evaluated the power of MB-MDR, for quantitative traits and unrelated individuals, in identifying gene–gene interactions for two different epistasis models. Scenarios with and without noisy data, as well as epistasis screening with and without lower-order effects adjustments, have been considered. Although our simulations only involved 10 SNPS, conclusions about observed patterns largely remain the same when increasing the number of genetic markers (results not shown). Note that an increasing number of SNPs will lead to an increasing number of interacting pairs, resulting in an elevated multiple testing burden, and hence resulting in reduced power. A first important finding is that MB-MDR adequately deals with one of the most major concerns in genetic association analysis studies (especially those targeting higher-order gene–gene interactions), namely avoiding that the overall type I rate is out of control (Table 2). The apparent slightly conservative results, obtained when MB-MDR screening explicitly accounts for lower-order main effects, are not surprising. Indeed, under the general null hypothesis of no genetic association, adjusting for main effects involves over-fitting and hence unnecessary over-correction. However, all the empirical estimates of the MB-MDR type I error rate in Table 2 fall within the interval (0.025, 0.075), satisfying Bradley's¹¹ liberal criterion of robustness. This criterion requires that the type I error rates are controlled for any level α of significance, if the empirical type I error rate α̂ is contained in the interval 0.5α≤α̂≤1.5α. We remark that as MB-MDR assesses global significance using resampling-based maxT-adjusted P-values, the family-wise error rate will always be weakly controlled at 5%, provided the assumptions of the Westfall and Young approach⁷ are attained.

A second important finding is that MB-MDR's power performance under different scenarios can be largely explained by the quantification of the actual genetic variance σ_gen² and by the decomposition of the total genetic variance into contributions of main effects and epistasis, and/or by the decomposition of main effects into additive and dominance variance. Empirical decompositions based on classical variance component analysis of Sham¹² are reported in Supplementary Tables S3 for M170 and Supplementary Tables S4 for M27 in the absence of GH, and in Supplementary Table S5 in the presence of GH. Each of these estimates is based on simulation setting's sample size (750 000 individuals). These results support our theoretically derived variance components, which are summarized in Table 3 (details to be provided elsewhere).

Table 3 Theoretically derived proportions of the genetic variance in error-prone or -free data due to main effects (additive and dominance) or epistasis

In particular, the observed lowest power performances of non-GH settings for GE10 and PM50 can be explained by the fact that over-representation of the minor allele as well as introducing phenotypic mixture result in a loss of actual genetic variance (Table 1) and therefore a loss of power. The theoretical results, indicating that a 50% reduction in total genetic variability is established when 50% phenotypic mixture is introduced in error-free data (Table 1), are supported by our empirical results (eg, Supplementary Table S3 for M170 and Supplementary Table S4 for M27) comparing σ_gen² with g².

When 50% GH is present, theory supports our empirical results in that the total actual genetic variance due to the two causal pairs of markers is twice the total actual genetic variance due to a single pair (Supplementary Table S5). Moreover, as we have introduced two possible genetic routes for an individual to be genetically predisposed for the trait of interest under GH (route 1 via SNP1 × SNP2 or route 2 via SNP3 × SNP4), the actual genetic variance in the pooled data will be half the genetic variance in the error-free data (see also Supplementary Table S5-ii for M170 and Supplementary Table S5-iv for M27). The total genetic variance due to a single causal pair approximates g²/4 (Supplementary Tables S5-i and S5-iii), which is due to the fact that the two pairs have the same minor allele frequencies. Therefore, the theoretical genetic variance is split between the two pairs and thereafter between the two SNPs. MB-MDR was shown to be rather robust in the presence of missing genotypes and genotyping error. Note that MB-MDR handles missing genotypes by using all available cases for the SNP pair under investigation. Hence, no individuals with missing data are a priori removed from the analysis, except when functional SNPs that are adjusted for in regression models have (partially) missing information.

A third finding is that accounting for important lower-order genetic effects in epistasis screening should be made standard. There is a debate about how to best model and test for both main effects and interactions or for interactions only when epistasis is present.¹³ Although a fully non-parametric screening approach (eg, such as MDR) is beautiful in that it does not require specifying particular genetic models, there is still a need to adjust for lower-order genetic effects via a parametric paradigm when targeting significant gene–gene interaction models. The MB-MDR offers a flexible framework to make these adjustments. For MDR-like applications other than MB-MDR, this is far from obvious. For instance, MDR for binary traits, Ritchie et al⁹ does not accommodate taking corrective measures for lower-order effects. Although significant main effects can be filtered out before an MDR screening, this happens at the cost of missing out on genuinely true interactions.

Furthermore, examining the decomposition of the total genetic variance has shed more light on the scenarios in which an adjusted MB-MDR analysis is warranted. For instance, when the minor allele frequency of the causal loci is 0.5, model M170 is a pure epistatic model (Supplementary Table S3: empirical estimates σ_epi²/σ_gen² approximate 1). Hence, in this scenario the effects of correcting for main effects are taken to the extreme. Clearly, any correction for lower-order effects would be an over-correction. On the other hand, as there is no true evidence for main effects in this model, any adjustment for main effects will only remove a small portion of the variability (Supplementary Table S3: M170, p=0.5; empirical estimates of σ_main²/σ_gen² are close to zero), resulting in false positives for the corrective analysis that are similar to those for the un-corrective analysis (Supplementary Table S2: M170, p=0.5; empirical estimates close to 5% also when not adjusting for main effects). In effect, the contribution of main effects becomes increasingly important with increasing p for M27 (≈32%, p=0.1, ≈61%, p=0.25 and ≈85%, p=0.5) and the reverse holds for M170 (≈59%, p=0.1, ≈11%, p=0.25 and ≈0%, p=0.5) (Table 3, Supplementary Tables S3 and S4).

For model M170 and GH scenarios involving p either 0.25 or 0.5 for the causal pairs, the epistatic variance explains a relatively large proportion of the total genetic variance in the data (σ_epi²/σ_gen²>87%; Supplementary Table S5-ii), and correcting for main effects therefore has little effect on power. In contrast, for Model M170 and p=0.1 for the causal pairs, main effects do make an important contribution to the total genetic variance (σ_main²/σ_gen²>57%; Supplementary Tables S5-i and S5-ii) compared with epistasis effects, which translates into a severe empirical power loss and power is dramatically reduced when proper accountancy for lower-order effects is being made (Figure 4).

Summarizing, dealing with phenotypic mixtures and GH will remain challenging for epistasis screening methods, for some time to come. Our empirical results suggest that more work is needed to better accommodate these particularities. Benefits may be gained from identifying the trait-specific factors (genetic or non-genetic) that best characterize mixed phenotypic populations. For GH, the genes in which the loci are present can be part of different etiological pathways leading to the same disease or be part of the same pathway. According to Heidema et al,¹⁴ irrespective of the biological mechanism that gives rise to GH, the association of the loci with the disease will be reduced if the total sample is used for measuring the association, as was done in this study. A method that is not robust in the presence of GH will most likely suffer from a decrease in power to detect genetic effects. As our main effects corrective analyses have suggested, a way forward may be to use methods to identify the latent classes and to adapt the epistasis screening accordingly.

Finally, any epistasis screening should properly account for lower-order effects to be able to claim that an identified interaction involves a significant epistatic contribution to the total genetic variance.

Software

The implementation of MB-MDR used in this paper was coded in C++. It is available upon request from the first author (jmahachie@ulg.ac.be).