Abstract
Here we show that sexual selection can have an effect on the rate of mutation. We simulated the fate of a genetic modifier of the mutation rate in a sexual population with and without sexual selection (modelled using a female choice mechanism). Female choice for ‘good genes’ should reduce variability among male subjects, leaving insufficient differences to maintain female preferences. However, female choice can actually increase genetic variability by supporting a higher mutation rate in sexually selected traits. Increasing the mutation rate will be selected against because of the resulting decline in mean fitness. However, it also increases the probability of rare beneficial mutations arising, and mating skew caused by female preferences for male subjects carrying those beneficials with few deleterious mutations (‘good genes’) can lead to a mutation rate above that expected under natural selection. A choice of two male subjects was sufficient for there to be a twofold increase in the mutation rate as opposed to a decrease found under random mating.
Similar content being viewed by others
Introduction
There is now evidence that female subjects can gain genetic quality benefits for their offspring when they choose to mate with ornamented male subjects (Petrie, 1994; Møller and Alatalo, 1999). This makes it even more difficult to explain how genetic variance is maintained in the preferred male trait and in any fitness-determining loci that are revealed by the trait (Ritchie, 1996). Theoretically, fitness variation among male subjects should rapidly be diminished, leaving insufficient differences to maintain female preferences. This problem of how genetic variation can be maintained under sexual selection is known as the ‘lek paradox’ (Kirkpatrick and Ryan, 1991).
A number of theories have been proposed to explain this paradox (Pomiankowski and Møller, 1995; Rowe and Houle, 1996; Holland and Rice, 1998; Wilkinson et al., 1998; Lesna and Sabells, 1999; Sheldon, 1999; Randerson et al., 2000; see Tomkins et al., 2004; for a review). Predominant among these are the idea that sexual traits are condition-dependent (condition being controlled by relatively large numbers of loci which together result in high levels of genetic variation) (Rowe and Houle, 1996), and the idea that variability is maintained by modifier genes (which act to increase the number of genes contributing to a trait) (Pomiankowski and Møller, 1995). However, these theories have been criticized on the grounds that non-sexual traits may also be condition-dependent and that modifier genes may themselves go to fixation (Turner, 1995; Neff, 2000). Others suggest that sufficient levels of genetic variation in fitness can be maintained as a result of frequency-dependent or temporally and spatially varying selection (Charlesworth, 1987; Rice, 1988; Hartl and Clark, 1989; Kokko and Lindstrom, 1996; Roff, 1998). However, evidence that additive genetic variation is actually higher in secondary sexual characters than in non-sexual traits (Pomiankowski and Møller, 1995; Petrie et al., ms) despite sexual traits being subjected to sexual and natural selection suggests that the maintenance of genetic variation under sexual selection remains a key problem in evolutionary biology.
Mutation is the source of genetic variation (Falconer and Mackay, 1996; Houle et al., 1996), yet it would appear unlikely that the maintenance of genetic variation in sexual traits could be explained by an adaptive increase in mutation rate. This is because, notwithstanding the finding that the optimum mutation rate may be higher (Leigh, 1973), selection will tend to drive the mutation rate downwards (Metzgar and Wills, 2000; Sniegowski et al., 2000). Nevertheless, recent work has highlighted modifiers of the mutation rate, in particular mutator genes, which were originally identified in bacteria (Cox, 1976). Simulations have shown how mutators could spread through asexual populations by hitch-hiking with beneficial mutations (Taddei et al., 1997; Tenaillon et al., 1999). They have also been demonstrated to increase the rate of adaptive evolution, at least in certain conditions (de Visser et al., 1999), though others have found that mutator lines did not differ in fitness (Sniegowski et al., 1997).
In sexual populations, recombination can be expected to disrupt hitch-hiking unless the mutator and associated beneficial mutation are strongly linked (Johnson, 1999; Partridge and Barton, 2000). Because of the increasing mutational load associated with the mutator, we would expect that once the beneficial becomes fixed, there will be selection for individuals in which reversion to the wild-type has occurred or in which recombination between the mutator and the loci under selection has occurred. As yet, there are few studies relating to these predictions (Gillespie, 1981; Tenaillon et al., 2000). However, this reasoning takes no account of the effects of sexual selection on the fate of mutator genes, and all recent simulation models in sexual populations have assumed random mating. Here, we show how one mechanism of sexual selection, female choice, can support an increase in mutation rate above that expected under natural selection, and we argue that this effect can contribute to the maintenance of genetic variability in fitness-related traits.
Methods
We simulated the fate of a modifier of the mutation rate in sexually reproducing populations with and without sexual selection. Our approach followed work on asexual populations (Taddei et al., 1997), and as in those simulations, the parameters reflected literature estimates where available, subject to the constraint that the model was intended as a simple abstraction of reality and not an attempt to simulate an entire genome. The simulations began by setting up a population of P individuals, half of each sex. Individuals were given a pair of homologous ‘chromosomes’ (i.e. we assume diploidy) each bearing a ‘mutator gene’ and an associated string of 10 ‘viability genes’. We do not assume that these genes constituted the entire genome; only that there are no interactions between the genes of interest and those at other sites and that all other things are equal. Each viability gene was subjected to a mutation process in which the rates of deleterious, lethal and beneficial mutations varied between simulations but were always given by d>l⩾b. The absolute rates of mutation were determined by the mutator gene M, which increased the rates of all types of mutation at the viability loci by a factor Bm where B was either 2 or 10 and m was initialized at zero and allowed to evolve through mutation. We assume that the mutator gene affected DNA repair only in a relatively small region of the genome (Metzgar and Wills, 2000), namely the set of viability genes referred to above, and we exclude from consideration unaffected areas. Furthermore, the mutator does not affect its own mutation rate. Mutations are more likely to disrupt the DNA repair mechanism than improve it, so we would expect that the rate of reversion of the mutator should be lower than the rate of mutation to the mutator genotype. However, so as not to bias the simulations in the direction of the mutator, we conservatively set the mutator gene so that m mutated upwards and downwards in increments of 1 with probability 10−3 in each direction. The mutator gene was assumed to be adjacent to the first of the row of viability genes, and the crossover rate between the mutator and the first viability gene was the same as between each other gene.
Individuals were subjected to a mortality process, whereby their probability of survival was a function of their genetic quality. Deleterious mutations were assumed to have larger phenotypic effects than beneficial mutations: deleterious mutations reduced the wild type fitness of 1 by 0.05; beneficial mutations increased it by 0.02, and individuals with lethal mutations had zero fitness (Taddei et al., 1997). The model assumed co-dominance with additive fitness effects, so the effects of mutations were summed to give genetic qualities, which determined individual survivorship in a mortality process. Therefore an individual in the first generation with two deleterious mutations at one locus, for example, would have had a 90% chance of surviving to breed. In later generations, fitness values were re-scaled as proportions of the maximum fitness in that generation.
Surviving individuals reproduced, either with random mating or with female choice. Random mating involved selecting a male and a female subject at random. In the case of female choice, a female subject was selected at random, and a set of F male subjects was selected at random. The female then bred with the male of highest genetic quality from that set. This ‘best of n’ rule is the most widely used rule in modelling female choice (Janetos, 1980; Johnstone and Earn, 1999). For each mating, one offspring was produced by bringing together chromosomes contributed by both parents. This was carried out by selecting a chromosome at random from each parent and allowing crossover between each adjacent gene with probability x. The process of selecting parents and producing offspring was repeated until the population was replaced by a new generation of P individuals.
Implicit in our model is the assumption that, in addition to determining survival, the mutations that a male accumulates determine the condition of some trait, which is used by female subjects in mate choice. Thus, we assume that a male's ‘good genes’ are ‘revealed’ in the trait and the female subjects use that information to select the best male. This assumption is supported by the literature on ‘good genes’ effects in sexual selection (Møller and Alatalo, 1999) and by the demonstration that sexual traits can reveal genetic quality (David et al., 2000; Hale et al., ms). It is also consistent with other sexual selection models (Kokko et al., 2002). For each mating, one offspring was produced by bringing together chromosomes contributed by both parents and allowing crossover between each adjacent genes.
All results were based on sets of 10 simulations, each of 20 000 generations. Unless otherwise stated, standard parameters used were population size P=1000 individuals, crossover rate between adjacent genes x=0.01; mutation rates for deleterious, lethal and beneficial mutations d=10−3, l=10−6 and b=10−6, respectively. These mutation rates were based as far as possible on available literature estimates (e.g. Drake et al., 1998). Mutation rates were in each case multiplied by the mutator value which was initialized at 20; the power mutated upwards and downwards in increments of 1 at a rate of 10−3 in each direction.
A second programme sharing similar assumptions was written in a different language (Visual Basic) by a different programmer (R Ascroft), showing that the results we obtained were not an anomalous feature of the programme or any subjectivity on behalf of the programmer.
Simulation results: evolution of mutation rate under sexual selection
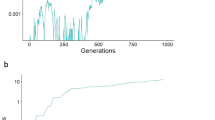
Given that an increase in mutation rate would have increased the number of deleterious mutations, we predicted that mutations in the mutator gene, which raised the mutation rate above the starting level, should have been selected against. This prediction was upheld in the case of random mating, but with female choice fixation of mutation rates of several times the starting parameters occurred (Figure 1).
Comparison between simulations with random mating (blue line) and with female choice (red line). The first of a set of 10 simulations is shown for each case in order to illustrate the evolutionary dynamics. The y axis displays the value of the mutator gene as a multiple of the initial mutation rate. Values plotted are means for each generation computed across the 1000 individuals. Mutation rates were d=10−3, l=10−6, b=10−6; crossover rate x=0.01; female choice F=1 for random mating, F=10 for choice. See Methods for simulation procedure and other parameters.
This shows that female choice has an effect on the evolution of a mutator gene when compared to random mating, but a key question is whether the level of female choice required is within a realistic range. We found that increasing female choice did increase the mean mutation rate, but that a choice of two male subjects was sufficient for there to be an approximately twofold increase in average rate (M=2.14±0.34), as opposed to the decrease found with no choice (M=0.35±0.14; t18=5.25, P<0.0005; Figure 2a). Our results therefore show that we require only that female subjects choose between two male subjects for there to be an effect on the evolution of the mutation rate.
The effect of female choice on genome evolution. Female choice is plotted as the number of randomly selected male subjects from which a female can choose the best. (a) Effect of female choice on the mutator gene (M), a modifier of the mutation rate, plotted as a multiple of the initial mutation rate. (b) Effect of female choice on beneficial mutations, plotted as the number accumulated per genome per generation. (c) Effect of female choice on deleterious mutations, plotted as the number accumulated per genome per generation. Parameters other than female choice are as for Figure 1.
What were the consequences for the evolutionary dynamics of new mutations? Comparing cases with no female choice and with choice between two male subjects, the number of beneficial mutations accumulating per genome per generation nb increased (nb=0.0057±9.9 × 10−5 and 0.086±1.5 × 10−3, respectively; t18=54.12, P<0.0005; Figure 2b) whereas the number of deleterious mutations nd decreased (nd=6.8 × 10−5±1.1 × 10−6 and 6.4 × 10−6±8.6 × 10−7, respectively; t18=45.29, P<0.0005; Figure 2c). As female choice increased further from 2 to 20 male subjects, beneficial mutations continued to increase, whereas deleterious mutations also showed some increase (Figure 2c). These processes reflect a balance between the strong selective effect of female choice in fixing beneficial and removing deleterious mutations, and the effect of the increasing mutation rate associated with increasing female choice, which results in more new mutations arising.
To test the strength of sexual selection in our simulations we calculated the variance in male mating success (Wade and Arnold, 1980). To give an illustrative example, we sampled from the midpoint (generation 10 000) of simulations with random mating and with female subjects choosing the best of 10 male subjects. In the latter case, the variance in male mating success was 17.98, considerably higher than the 2.19 found under random mating. Thus, our female choice rule was effectively implementing sexual selection. Nevertheless, the way we implemented the ‘best of n’ algorithm by allowing female subjects to choose from different sets of male subjects meant that the mating skew at a population level was relatively low. Thus, in the above example, the maximum number of matings achieved by any one male was 24, or 2.4% of those available (compared with 0.7% under random mating). This is low compared with estimates from lekking species (Höglund and Alatalo, 1995).
Sexual selection or natural selection?
Our results might be due to the strength of selection rather than to sexual selection operating in a different manner from natural selection. To test this, we ran simulations in which there was no female choice but instead there was a second round of natural selection (the fitness-dependent mortality process). The effect of the extra round of natural selection was evident both in the reduced number of deleterious mutations (which decreased from 6.78 × 10−5±1.05 × 10−6 per genome per generation to 4.68 × 10−5±8.33 × 10−7, t18=−15.63, P<0.0005) and the increased number of beneficials (from 5.66 × 10−3±9.93 × 10−5 to 8.48 × 10−3±1.17 × 10−4, t18=18.40, P<0.0005). However, despite these clear effects of direct selection, there was no evidence of indirect selection on the mutator, which remained unchanged (at 3.51 × 10−4±4.58 × 10−5 and 4.44 × 10−4±5.56 × 10−5 times the initial mutation rate, respectively, t18=1.28, P=0.216). Therefore, increasing the strength of natural selection did not allow for an increase in the rate of mutation. Intuitively, this is not surprising as natural selection will act to reduce the mutation rate as this produces a net survival cost to the individual. Sexual selection, on the other hand, can result in the evolution of traits that carry survival costs, like the peacock's train, which is heavy and cumbersome to carry around (Petrie, 1992). Sexual selection as we have shown can result in an increase in mutation rate. We have shown that female choice which results in a variance in male mating success can have this effect.
Realistically, female subjects may not always choose the best male subjects, whether because phenotype is influenced by environmental effects as well as genotype; because of imperfect discrimination by female subjects; or because of costs associated with searching for and selecting the best male subjects. Allowing for imperfect female choice did reduce the magnitude of the effect of sexual selection on the mutator, but did not eliminate it. For example, with female subjects choosing the best of two male subjects with probability 0.75 the mean mutator was 1.14±0.19, which was less than that for perfect selection of the best of two male subjects (2.14±0.34, t18=2.56, P=0.02) but nevertheless greater than that for random mating (0.35±0.046, t18=3.97, P=0.001).
Although we have modelled female choice explicitly, other mechanisms of sexual selection that result in variance in male mating success could theoretically also have the effect of opposing natural selection and allowing the evolution of an increase in the rate of mutation, by whatever mechanism this is achieved. For example, male/male competition acting on say a genetic modifier of the rate of recombination may also have the same main result of sexual selection promoting genetic variation. However, confirmation of this must await further detailed modelling which is currently beyond the scope of this present paper.
Are our results peculiar to sexual selection? Could another form of selection result in the same effect? Our results suggest that all that is necessary for the maintenance of an increased mutation rate (which is under genetic control) is a genetic benefit that outweighs the genetic costs of an increase in mutation rate. Female choice for good genes in our model provides that genetic benefit, and this is realistic as there is ample evidence from nature that this occurs. It is possible that some other genetic benefit could also overcome the inevitable genetic costs associated with an increased mutation rate. For example, some form of kin selection/group selection/demic selection may provide the same effect. However, while it is known that kin selection can outweigh the costs of altruism (Hamilton's rule) no one has considered the possibility that kin selection could maintain an elevated mutation rate, and no one has modelled this. Although we would dearly like to explore the other possibilities suggested by our model and our results this must remain a task for the future as it is beyond the scope of this paper.
Some workers argue that it is unnecessary to distinguish between sexual and natural selection and that sexual selection is a form of natural selection. This is true in a strict sense and as argued clearly by Stearns and Hoekstra (2000) many traits besides sexually selected characters reduce survival, including reproduction itself. However, although Darwin's distinction between natural and sexual selection is not logically necessary it is however extremely useful in understanding the evolution of traits, including processes at the level of genome, that also carry survival costs.
What happens to variance in fitness?
Compared to the random mating case, we have shown that sexual selection can cause the mutation rate to increase. However, in order to show that this can resolve the lek paradox, we need to show that this increase in mutation rate counters the loss of variance in fitness that otherwise results from female choice. Sexual selection (as represented by an increase from 1 to 10 in the number of male subjects from which female subjects can select the best) reduced variance between individuals in their numbers of both beneficial (1.84±0.41 and 0.33±0.05; t18=3.62, P=0.005) and deleterious (1.92±0.15 and 0.037±0.004; t18=12.24, P<0.0005) mutations (Figure 3). However, this reduction in variance was less in the presence of a mutator gene that allowed evolution of higher mutation rates. This is shown by the fact that, under female choice, variances were higher when mutation rate was variable than when it was constant (for beneficial mutations variances were 1.07±0.22 and 0.33±0.05, respectively, t18=3.33, P=0.008; and for deleterious mutations, 0.56±0.13 and 0.037±0.004 respectively, t18=3.90, P=0.004). There is therefore evidence both that mutation rates can evolve upwards under female choice and that this effect can counteract the effect of female choice in reducing variance.
Variance in fitness in relation to sexual selection and mutation rate. Variance in fitness is expressed as variance in numbers of (a) beneficial and (b) deleterious mutations. Random mating (where female subjects mate with a randomly selected male) is compared with female choice (where female subjects mate with the male of highest genetic quality of 10 randomly chosen male subjects). Mutation rate is either held constant (at rates d, l and b) or is allowed to vary as some multiple of these rates as determined by a mutator gene. Parameters as in Figure 1 unless otherwise indicated.
What is the effect of varying the parameters used?
How robust is our finding that mutation rates can increase under female choice to variations in the parameters used? A key parameter is the rate of beneficial mutations: as it is so difficult to measure empirically, it is particularly important to know how dependent are our results on this factor. We found that decreasing the rate of beneficial mutations by several orders of magnitude while holding deleterious mutations constant had little effect on the fate the mutator (Figure 4a). In contrast, decreasing the rate of deleterious mutations while holding the rate of beneficials constant had a more marked effect (Figure 4b). However, these results are contingent on a particular set of parameter values and therefore must be treated with caution. Further simulations are required to fully investigate all combinations of rates of beneficial and deleterious mutations.
Evolution of the mutator in relation to (a) varying rates of beneficial mutations while holding deleterious mutations at 10−3; (b) varying rates of deleterious mutations while holding beneficial mutations at 10−6; (c) rate of crossing over, plotted as probability of a break occurring between any two genes. Parameters as in Figure 1 unless otherwise indicated.
Examining the effects of other parameters, as population size increased from 250 individuals to 2000, mean mutator increased from 2.30±0.40 to 12.81±2.34. Lowering the rate of mutation in the mutator gene itself lowered the mean level of the mutator from 6.36±1.44 with rates of 10−3 both forwards and backwards to 1.32±2.56 with rates of 10−6. Correspondingly, when the forward rate (10−3) was higher than the backward rate (10−6) the mean mutator increased to 24.04±0.95, whereas when the rates were reversed it decreased to 0.10±0.02. Given that mutations are more likely to disrupt the DNA repair mechanism than improve it (Taddei et al., 1997), we would expect that the rate of reversion of the mutator should be lower than the rate of mutation to the mutator genotype, so we predict an increase in mean mutator level rather than a decrease. Changing the increments by which the mutator evolved had little effect on the results (with random mating the mean mutator was 0.35±0.05 when it incremented in powers of 2, compared with 0.1553±0.0289 when incrementing with powers of 10; whereas with female choice 10, the mutator was 6.36±1.44 when it incremented in powers of 2 versus 6.5726±0.6639 when it incremented in powers of 10.
Why does female choice have such an effect on the fate of mutator genes? Previous theory concerning increases in mutation rate has emphasized the role of hitch-hiking of a mutator gene with a closely linked beneficial mutation (Taddei et al., 1997). The unstable dynamics we observed were similar to those reported by these authors, suggesting that similar processes may have been at work. We therefore expect the mutator to be sensitive to the rate of crossing over: because it is disadvantageous, it should be lost as soon as any beneficial to which it is linked has reached fixation. Consistent with this argument, we found that the mutator did decrease from 8.77±1.32 with a 0.005 probability of a break between any two adjacent genes, to 5.37±0.96 with a 0.05 probability. We consider this to be a relatively high rate of crossing over, given our assumption that we are dealing with a mutator that affects only a set of closely linked genes over a small region of a chromosome. There remains a substantial increase in the mutation rate despite the fact that the mutator and the furthest of the 10 genes were then assorting independently.
Evidence for the robustness of our results is provided by the fact that a separate set of simulations developed by another programmer in a different language showed a similar contrast between an increase in the mutator gene under female choice and its decline under random mating.
At the end of the day it must be borne in mind that the results, although controversial, are based on a comparison of two situations, one with female choice and one without. The genetic architecture, rate of crossing over, population size and so on are identical in both conditions; the only difference comes when a female has a chance to mate with the better of two male subjects.
Discussion: a self-sustaining resolution to the lek paradox
Our results show that mutation rate can increase under sexual selection, and that this process counteracts the reduction in genetic variance caused by sexual selection. The effect appears to be owing to hitch-hiking of a mutator gene with beneficial mutations. Such an effect has been reported in bacteria but was thought to be less prevalent in sexual systems owing to recombination (Johnson, 1999; Tenaillon et al., 2000). Our finding is that sexual selection has a decisive effect on whether a mutator can increase in a sexual population. Why should hitch-hiking of a mutator be more prevalent under sexual selection? Assuming that accumulated mutational load is apparent through some revealing trait (Pomiankowski et al., 1991), and assuming that female subjects choose male subjects on the basis of this trait, then female subjects will be able to select to breed with those male subjects that carry the beneficial mutations that are associated with the mutator gene, but which have accumulated relatively few of the deleterious mutations that will also be more common among those carrying the mutator. Thus, although the mutator is not selected directly, female choice acts on it indirectly, facilitating its establishment and reducing the rate at which it is lost. There is a further advantage to male subjects in this system. Male subjects of high genetic quality will on average have greater mating success and this could also result in the costly mutator gene becoming established and maintained in the population. The cyclical dynamics we observe by which mutators arise, are maintained for several generations and are lost are similar to those reported for asexual populations (Tenaillon et al., 1999). This discussion highlights an important distinction between the hitch-hiking process and the process proposed by Pomiankowski and Møller (1995) by which variance is maintained through the operation of genetic modifiers. In their model, an accelerating fitness function means that increasing variance is adaptive. In ours, the spread of the variance-increasing modifier is actually maladaptive.
Our results have implications for the problem of how variability is maintained under sexual selection, the lek paradox. A successful resolution to this problem has remained elusive, despite a number of recent theories. Previously, female choice has been thought to reduce variation, but we have shown here that it can actually select for continued generation of variation through mutational input in those traits, which are subject to sexual selection. The crucial aspect of our mechanism is that, unlike other proposed mechanisms, it is self-sustaining. It has previously been shown that variance among male subjects is required for female choice to be adaptive (Petrie and Lipsitch, 1994); now we have gone full circle by showing that choice promotes variability, and so will itself increase the selection pressure for choice.
The mechanism explicitly involves ‘good genes’ effects: we assume female subjects prefer male subjects of high genetic quality and that genetic quality is revealed in sexual ornamentation. However, while we have framed our model in terms of female choice, we would stress that any mechanism of sexual selection (such as male–male competition or sperm competition) that resulted in mating skew in favour of those of highest genetic quality is equally compatible with our model. That is, were the male of highest genetic quality to win a contest among n male subjects to mate with a female, we would obtain precisely the same results.
Is the effect we find particular to sexual selection? This is difficult to know as without modelling different forms of selection that can oppose survival costs we will not know, and this would require extensive further work. In particular, it would be very interesting to model those forms of selection that have been developed to explain costly altruism (for example, group selection) which may also allow for an elevated mutation rate. Interestingly, sexual selection has also been invoked to explain costly altruism (Roberts, 1998). Sexual selection is a widely recognized mechanism that operates counter to natural selection and can act to produce higher mutation rates, in an exactly analogous way to how sexual selection produces and maintains morphological traits (such as the peacock's train) that are costly under natural selection.
Although it is increasingly being recognized that adaptability may itself be subject to selection, the processes that could increase adaptability are not thought to operate in sexual organisms (Partridge and Barton, 2000). Our results contrast with this theory and show that there are mechanisms whereby adaptability may be increased in sexual populations. However, our model does require a continued need for adaptation. The models assume that it is possible to improve the genome, even if only very rarely and by a small degree. We therefore still require explanations of what is driving the need for adaptation, whether it be evolutionary arms races between parasites and hosts (Hamilton and Zuk, 1982) or male subjects and female subjects (Holland and Rice, 1998).
We have advanced a hypothesis about how variability could be maintained under female choice. Whether factors that control the mutation rate, be they mutators or some other mechanism (e.g. modifiers of the recombination rate (Burt and Bell, 1987)), operate in the way proposed by our model is a matter for empirical investigation. Our theory predicts that sexual selection will not lead to the fixation of variation in male sexual characters and that there will continue to be genetic benefits from female choice. Consistent with this, inter-specific variation in the proportion of extra-pair offspring is positively related to genetic variability (Petrie et al., 1998). Our mechanism can explain how, despite being subject to strong directional selection, sexual traits can be more phenotypically variable and have higher additive genetic variation than non-sexual traits (Pomiankowski and Møller, 1995). We predict that there should be a higher mutation rate in sexually selected species, particularly where female subjects choose among a large number of male subjects and where this results in high mating skew (Höglund and Alatalo, 1995), and that mutation rates will be higher in sexual as opposed to non-sexual traits, as a mutation modifier associated with such traits will be selected against. Furthermore, the greater accumulation of beneficial mutations that we observed with female choice leads us to predict that there will be a higher rate of evolution in sexually selected lineages. There are no direct tests but there is some evidence that is consistent: the Y chromosome in mammals mutates four to seven times faster than the X in mammals, as does the Z in birds (Ellegren and Fridolfsson, 1997). A recent study of the male to female mutation bias (αm) which was estimated by comparing Z-linked and W-linked substitution rates in gametologous introns found that αm differences between avian clades positively covaried with both generation time and sexual selection measured as the frequency of extra pair paternity (Bartosch-Harlid et al., 2003). Møller and Cuervo (2003) have recently found evidence for an increased mutation rate in species with more intense sexual selection. Increased mutation was not associated with increased sperm production, and they independently suggest that species with intense sexual selection may maintain elevated mutation rates because sexual selection continuously benefits viability alleles expressed in condition-dependent characters.
Our results could also be important in understanding the maintenance of sexual reproduction. Theoretical work on the evolution of sex has tended to assume that individuals mate randomly, yet our simulations illustrate just how powerful is mate choice in determining the evolutionary dynamics of new mutations (Agrawal, 2001; Siller, 2001). This means that, whether the advantages of sex lie in bringing beneficial combinations together or removing deleterious mutations (Barton and Charlesworth, 1998), mate choice and its effect on mutation rate could shift the balance of costs and benefits towards sexual reproduction.
Lastly, we have modelled a genetic modifier of the mutation rate or a mutator gene, but we predict that our results, which demonstrate the role of sexual selection on the maintenance of genetic variation, are not exclusive to this particular mechanism but will operate on any other costly genetic mechanism that introduces genetic variation, for example, recombination (which is not a genome-wide mechanism).
To conclude, our simulation model shows that organisms with some form of sexual selection can potentially deal with higher mutational loads/rates, although the applicability of the model to real systems is unclear and needs empirical testing. We would also like to see the development of further models along similar lines and hope that one day an analytical model could be developed to fully test the generality of the theoretical idea.
References
Agrawal AF (2001). Sexual selection and the maintenance of sexual reproduction. Nature 411: 692–695.
Barton NH, Charlesworth B (1998). Why sex and recombination? Science 281: 1986–1990.
Bartosch-Harlid A, Berlin S, Smith NGC, Møller AP, Ellegren H (2003). Life history and the male mutation bias. Evolution 57: 2398–2406.
Burt A, Bell G (1987). Mammalian chiasma frequencies as a test of two theories of recombination. Nature 326: 803–805.
Charlesworth B (1987). The heritability of fitness. In: Bradbury JW, Andersson MB (eds) Sexual Selection: Testing the Alternatives. John Wiley & Sons: Chichester. pp 21–40.
Cox EC (1976). Bacterial mutator genes and the control of spontaneous mutation. Annu Rev Genet 10: 135–156.
David P, Bjorksten T, Fowler K, Pomiankowski A (2000). Condition-dependent signalling of genetic variation in stalk-eyes flies. Nature 406: 186–188.
de Visser JAGM, Zeyl CW, Gerrish PJ, Blanchard JL, Lenski RE (1999). Diminishing returns from mutation supply in asexual populations. Science 283: 404–406.
Drake JW, Charlesworth B, Charlesworth D, Crowe JF (1998). Rates of spontaneous mutation. Genetics 148: 1667–1686.
Ellegren H, Fridolfsson AK (1997). Male-driven evolution of DNA sequences in birds. Nat Genet 17: 182–184.
Falconer DS, Mackay TFC (1996). Introduction to Quantitative Genetics. Longman: London.
Gillespie JH (1981). Mutation modification in a random environment. Evolution 35: 468–476.
Hale M, Verduijn MH, Møller AP, Wolff K, Petrie M (ms). The peacock's train is an honest signal of genetic quality at the major histocompatibility complex. Nature Genetics (submitted).
Hamilton WD, Zuk M (1982). Heritable true fitness and bright birds: a role for parasites. Science 218: 384–387.
Hartl DL, Clark AG (1989). Principles of Population Genetics. Sinauer: Sunderland, MA.
Höglund J, Alatalo RV (1995). Leks. Princeton University Press: Princeton.
Holland B, Rice WR (1998). Chase away sexual selection: antagonistic seduction versus resistance. Evolution 52: 1–7.
Houle D, Morikawa B, Lynch M (1996). Comparing mutational variabilities. Genetics 143: 1467–1483.
Janetos AC (1980). Strategies of female mate choice: a theoretical analysis. Behav Ecol Sociobiol 7: 107–112.
Johnson T (1999). Beneficial mutations, hitchhiking and the evolution of mutation rates in sexual populations. Genetics 151: 1621–1631.
Johnstone RA, Earn DJD (1999). Imperfect female choice and male mating skew on leks of different sizes. Behav Ecol Sociobiol 45: 277–281.
Kirkpatrick M, Ryan MJ (1991). The evolution of mating preferences and the paradox of the lek. Nature 350: 33–38.
Kokko H, Brooks R, McNamara JM, Houston AI (2002). The sexual selection continuum. Proc R Soc Lond B 269: 1331–1340.
Kokko H, Lindstrom J (1996). Evolution of female preference for old mates. Proc R Soc Lond B 263: 1533–1538.
Leigh EG (1973). The evolution of mutation rates. Genetics 73: 1–18.
Lesna I, Sabells MW (1999). Diet dependent female choice for males with ‘good genes’ in a soil predatory mite. Nature 401: 581–584.
Metzgar D, Wills C (2000). Evolutionary changes in mutation rates and spectra and their influence on the adaptation of pathogens. Microbes Infect 2: 1513–1522.
Møller AP, Alatalo RV (1999). Good genes effects in sexual selection. Proc R Soc Lond B 266: 85–91.
Møller AP, Cuervo JJ (2003). Sexual selection, germline mutation rate and sperm competition. BMC Evol Biol 3: 6.
Neff BD (2000). Females aren't perfect: maintaining genetic variation and the lek paradox. Trends Ecol Evol 15: 395.
Partridge L, Barton NH (2000). Evolving evolvability. Nature 407: 457–458.
Petrie M (1992). Peacocks with low mating success are more likely to suffer predation. Anim Behav 44: 585–586.
Petrie M (1994). Improved growth and survival of offspring of peacocks with more elaborate trains. Nature 371: 598–599.
Petrie M, Cotgreave P, Pike TW (ms). Variation in the peacock's train shows a genetic component. Heredity (submitted).
Petrie M, Doums C, Møller AP (1998). The degree of extra-pair paternity increases with genetic variability. Proc Natl Acad Sci USA 95: 9390–9395.
Petrie M, Lipsitch M (1994). Avian polygyny is most likely in populations with high variability in heritable male fitness. Proc R Soc Lond B 256: 275–280.
Pomiankowski A, Iwasa Y, Nee S (1991). The evolution of costly mate preferences. I. Fisher and biased mutation. Evolution 45: 1422–1430.
Pomiankowski A, Møller AP (1995). A resolution of the lek paradox. Proc R Soc Lond B 260: 21–29.
Randerson JP, Jiggins FM, Hurst LD (2000). Male killing can select for male mate choice: a novel solution to the paradox of the lek. Proc R Soc Lond B 267: 867–874.
Rice WR (1988). Heritable variation in fitness as a prerequisite for adaptive female choice: the effect of mutation-selection balance. Evolution 42: 817–820.
Ritchie M (1996). What is ‘the paradox of the lek’? Trends Ecol Evol 11: 175.
Roberts G (1998). Competitive altruism: from reciprocity to the handicap principle. Proc R Soc Lond B 263: 427–431.
Roff DA (1998). The maintenance of phenotypic and genetic variation in threshold traits by frequency-dependent selection. J Evol Biol 11: 513–529.
Rowe L, Houle D (1996). The lek paradox and the capture of genetic variance by condition dependent traits. Proc R Soc Lond B 263: 1415–1421.
Sheldon BC (1999). Revealing quantitative genetic relationships in sexual selection using molecular markers. In: Adams N, Slotow R (eds) Proceedings of the 22nd International Ornithology Congress, Durban. Birdlife South Africa: Johannesburg. pp 1099–1114.
Siller S (2001). Sexual selection and the maintenance of sex. Nature 411: 689–692.
Sniegowski P, Gerrish PJ, Jonson T, Shaver A (2000). The evolution of mutation rates: separating causes from consequences. Bioessays 22: 1057–1066.
Sniegowski PD, Gerrish PJ, Lenski RE (1997). Evolution of high mutation rates in experimental populations of E. coli. Nature 387: 703–705.
Stearns SC, Hoekstra RF (2000). Evolution: An Introduction. Oxford University Press: New York.
Taddei F, Radman M, Maynard Smith JM, Toupance B, Gouyon PH, Godelle B (1997). Role of mutator alleles in adaptive evolution. Nature 387: 700–702.
Tenaillon O, Le Nagard H, Godelle B, Taddei F (2000). Mutators and sex in bacteria: conflict between adaptive strategies. Proc Natl Acad Sci USA 97: 10465–10470.
Tenaillon O, Toupance B, Le Nagard H, Taddei F, Godelle B (1999). Mutators, population size, adaptive landscape and the adaptation of asexual populations of bacteria. Genetics 152: 485–493.
Tomkins JL, Radwan J, Kotiaho JS, Tregenza T (2004). Genic capture and resolving the lek paradox. Trends Ecol Evol 19: 323–328.
Turner GF (1995). The lek paradox resolved? Trends Ecol Evol 10: 473–474.
Wade MJ, Arnold SJ (1980). The intensity of sexual selection in relation to male sexual behavior, female choice, and sperm precedence. Anim Behav 28: 446–461.
Wilkinson GS, Presgraves DC, Crymes L (1998). Male eye span in stalk eyed flies indicates genetic quality by meiotic drive suppression. Nature 391: 223–224.
Acknowledgements
We are grateful to Malte Andersson, Jack Bradbury, Andre Gilburn, GK Chambers, Andrew Cockburn, L Morris Gosling, Geoff Graves, Mark Hauber, Mike Jennions, Teresa Jones, Rebecca Kilner, Tom Kirkwood, Loeska Kruuk, Mike Magrath, Rob Magrath, Raoul Mulder, Anders Pape Møller, Richard Nichols, Geoff Parker, Andrew Pomiankowski, Mike Ritchie, Gunilla Rosenqvist, Locke Rowe, Tom Sherratt, Ilik Saccheri, Dave Shuker, Tom Tregenza and Nina Weddell and a number of anonymous referees for comments and discussion. We are particularly grateful to Geoff Parker for his unfailing encouragement during the long gestation of this idea (and our 10 previous attempts to publish it) and S Mahmoodi and R Ascroft for programming support. GR modelled an original idea of MP, which she first submitted as sole author in January 1997.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Petrie, M., Roberts, G. Sexual selection and the evolution of evolvability. Heredity 98, 198–205 (2007). https://doi.org/10.1038/sj.hdy.6800921
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/sj.hdy.6800921
Keywords
This article is cited by
-
Heritability of morphological and behavioural traits in evolving robots
Evolutionary Intelligence (2023)
-
Sexual selection for males with beneficial mutations
Scientific Reports (2022)
-
Selection for male stamina can help explain costly displays with cost-minimizing female choice
Behavioral Ecology and Sociobiology (2022)
-
Experimental evidence for effects of sexual selection on condition-dependent mutation rates
Nature Ecology & Evolution (2020)
-
A Paradox of Genetic Variance in Epigamic Traits: Beyond “Good Genes” View of Sexual Selection
Evolutionary Biology (2016)