Abstract
Limited dispersal distances in plant populations frequently cause local genetic structure, which can be quantified by spatial autocorrelation. In clonal plants, three levels of spatial organization can contribute to positive autocorrelation; namely, the neighbourhood of (a) ramets, (b) clone fragments and (c) entire clones. Here we use data from an exhaustive sampling scheme on a clonal plant to measure the contribution of the neighbourhoods of each distinct clonal structure to total spatial autocorrelation. Four plots (256 grid points each) within dense meadows of the marine clonal plant Zostera marina (eelgrass) were sampled for clone structure with nine microsatellite markers (≈80 alleles). We found significant coancestry (fij), at all three levels of spatial organization, even when not allowing for joins between samples of identical genets. In addition, absolute values of fij and the maximum distance with significant positive fij decreased with the progressive exclusion of joins between alike genotypes. The neighbourhood of this clonal plant thus consists of three levels of organization, which are reflected in different kinship structures. Each of these kinship structures may affect the level of biparental inbreeding and the physical distance between flowering shoots and their outcrossing neighbourhood. These results also emphasize the notion that spatial autocorrelation crucially depends on the scale and intensity of sampling.
Similar content being viewed by others
Introduction
Spatially limited dispersal in many plant species has led to the prediction that plant populations show kinship structure on a local scale (Levin and Kerster, 1971; Bradshaw, 1972; Heywood, 1991). In addition, plant–plant interactions that involve competition and/or facilitation are usually limited to the immediate neighbourhood of a particular individual (Harper, 1977). Hence, kinship structuring in the immediate neighbourhood can lead to interactions, such as competition for outcrossing opportunities (Price and Waser, 1979), between close relatives. Such local genetic structure is likely to influence the evolutionary dynamics of a population (Maynard Smith, 1976; Nakamura, 1980) and therefore needs to be quantified.
Genetic structuring in natural populations can be quantified by spatial autocorrelation (Sokal and Oden, 1978a). In general, spatial autocorrelation can be defined as the property of variables taking values, at pairs of locations a certain distance apart, that are more similar (positive autocorrelation) or less similar (negative autocorrelation) than expected for randomly associated pairs of observations (Legendre, 1993). Under limited dispersal of seeds and/or pollen, nearest neighbours should provide the highest autocorrelation because kinship is expected to diminish monotonically with distance (Kimura and Weiss, 1964).
Spatial autocorrelation of genotypic data has been investigated mainly in nonclonal plant species (Sokal and Oden, 1978a; Legendre, 1993; Smouse and Peakall, 1999; reviewed in Heywood, 1991). In contrast, clonal plants that often dominate aquatic and terrestrial vegetation (van Groenendael and de Kroon, 1990; Klimes et al, 1997) need special attention. The complex growth geometry in this large group of successful plant species prohibits straightforward use of spatial autocorrelation. The physical connections between shoots often breaks over time through rotting of their rhizomes and/or disturbance events. The loss of physical connections facilitates the formation of spatially separated clusters of rhizomes from a single genotype. Hence, we can distinguish three distinct levels of spatial organization of clones, namely: (a) Ramets corresponding to rhizome modules with a variable degree of physiological integration (Watson and Casper, 1984; Callaghan et al, 1992) which are organized in (b) clone fragments (spatial aggregations of ramets), separated by intruding growth of other genotypes and/or disturbance, and finally (c) the entire clone as the sum of all ramets belonging to one distinct multilocus genotype. Owing to the spatial disruption of clones, the genetic individuals can often only be reconstructed after sampling and subsequent identification with genetic markers (Sydes and Peakall, 1998; Suzuki et al, 1999).
Most studies, using autocorrelation of genotypic data in clonal plants, have focused on quantifying the degree of aggregation for units of single clones within sampled areas (clonal structure (a) from above) (Caujape-Castells and Pedrola-Monfort, 1997; Caujape-Castells et al, 1999; Major and Odor, 1999; Suzuki et al, 1999; Burke et al, 2000). However, including all possible joins between samples in spatial autocorrelation of a clonal plant, without taking the spatial spread of the genetic individuals into account, will have the effect that significant autocorrelation may be due to both limited gene flow and clonal growth, which cannot be distinguished from one another (Reusch et al, 1999b).
The aim of the present study was to use genotypic data from an extensive fine-scale sampling in monospecific meadows of the clonal plant Zostera marina along the Baltic Coast. Our goal was (i) to evaluate the contributions of the three levels of clonal structure to spatial autocorrelation, and hence to local kinship structure and (ii) to test whether kinship structure in the local neighbourhood of clones is higher than expected from random dispersal. We expected a decrease in the absolute values of coancestry and in the maximum distance with significant spatial genetic structure with the progressive exclusion of joins between like genotypes. In addition, from the empirical evidence of limited dispersal in this species, we expected to find kinship structure beyond the spatial spread of clones. Sampling was extensive both spatially (1 m intervals, 256 grid points, four plots) and genotypically (nine microsatellite markers representing ≈80 alleles). We used regularly spaced lattices of sampling points for their desirable properties in an autocorrelation context (Epperson, 1993). The lattices were square plots to minimize edge effects and the plots were replicated both within and between two populations to verify that the spatial scale of sampling was within the context of a larger spatial pattern (Epperson, 1993).
Materials and methods
Study species, area and sampling
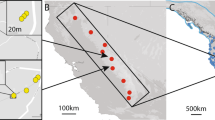
Z. marina (eelgrass) is a marine angiosperm with a true subaqueous mating system (den Hartog, 1970). Along the nontidal Baltic Coast, the species is perennial and forms dense meadows through a mixture of sexual reproduction and clonal growth. In each of two Baltic Z. marina populations, we sampled two 15-m × 15-m plots on a regular grid in 1-m intervals using SCUBA. The ‘Falkenstein’ population grows on the west side of the Kiel Förde, Schleswig Holstein (54°24′ N, 10°12′ E) in 3–3.5 m water depth. The ‘Maasholm’ population grows in an estuary at the mouth of the river Schlei, Schleswig Holstein (54°41′ N, 10°00′ E) in 1.5–2.5 m water depth. The ‘Maasholm’ population grows in an embayment and depending on the speed and direction of the wind, the water level can vary up to 60 cm (Marahrens, 1995). The shallower waters of Maasholm make this population prone to disturbance by swan grazing and ice scour.
Leaf material (3–5 cm) of the shoots closest to the grid points was collected and preserved through drying in silica-gel for DNA amplification. Total genomic DNA was extracted with the Qiagen plant DNA extraction kit (Qiagen, Hilden, Germany). The DNA-extract was processed in two combined PCR-amplifications using nine polymorphic microsatellite markers specifically designed for Z. marina (representing ≈80 alleles). PCR-reactions with fluorescently labelled primers followed standard protocols (Reusch et al, 2000). Alleles were scored on ABI 377 and ABI 3100 automated sequencers, using the software packages GeneScan 3.1 or 3.7 and Genotyper 2.0 or 3.7 (Biosystems, 1998, 2001). Intercalibration samples assured consistent allele designation across both sequencers. This produced 256 pixel images of the genet composition in the plots (Figure 1) (Hämmerli and Reusch, 2003). All typed samples of one distinct genotype in each plot were treated as a clone. No clone occurred in more than one plot and the likelihood that ramets were erroneously assigned to the same genet because they exhibited the same nine-locus genotype by chance was very small (all Pgen≪0.001) (Parks and Werth, 1993). We detected weak linkage disequillibrium between some loci which were however different between sampling locations. Hence, there was no indication for physical linkage among the used markers (see also Hämmerli and Reusch, 2003).
Sampling grid of a 15 m × 15 m plot in a continuous meadow of Z. marina (eelgrass) in c. 3 m water depth off the Baltic Coast. Gridpoints are indicated by running numbers for each distinct multilocus genotype detected through genotyping leaf samples from each grid point with nine polymorphic microsatellite markers.
Autocorrelation analysis with multilocus genotypes
Patterns of spatial genetic autocorrelation are scale dependent and therefore influenced by the chosen sampling scheme (Epperson, 1993). For example, the spatial scale of sampling should be smaller than the spatial autocorrelation (Sokal and Oden, 1978b; Epperson and Li, 1997) and each distance class should contain an adequate number of pairwise comparisons (N>60) to give reliable autocorrelation estimates (Doligez and Joly, 1997; Epperson and Li, 1997).
We performed spatial autocorrelation on the genotypic plot data from the two populations to quantify the genetic structure and to assess the effect of a decomposition of clonal structure on autocorrelation estimates. For the pairwise comparison, we generated three different data sets ((a)–(b)–(c)) using MATLAB 6.12. codes (Math Works, 2000). Each data set corresponds to one aspect of the clonal structure as illustrated in Figure 2 and described in Table 1.
-
a)
Including all samples, this analysis most closely quantifies the genetic neighbourhood of ramets.
-
b)
Including only one sample from each clone fragment with a rooks definition of neighbourhood (horizontal or vertical connection between grid points). This analysis quantifies the genetic neighbourhood of clone fragments. Other neighbourhood definitions (eg queens definition) yield similar results. The coordinates were moved to the centre point of each fragment. The centre points were calculated as S(xy) = Σij(x,y)ij/ni where x,y are the grid coordinates of the j sample of clone i and n is the total number of samples of clone i.
-
c)
Including only the centre point of the largest clone fragment. This analysis quantifies the genetic neighbourhood of entire clones. If≥2 large fragments had the same area, one of the largest fragments was chosen at random. Here we present only the analysis with the largest fragments. Other choices of fragments such as the smallest or a random fragment yielded similar results.
Definition of joins among genotypes in Z. marina (eelgrass) representing three different subsets of genotypic data that were analysed with spatial autocorrelation using multilocus microsatellite genotypes: (a) Including all samples of each clone, (b) centre points of all fragments of each clone and (c) centre point of the largest fragment of each clone. Only one clone is presented in the figure for reasons of clarity. The two circles in each plot represent the two shortest distance classes used in the autocorrelation (d1=1 m and d2=2 m) and illustrate the progressive exclusion of joins between like genotypes (a–c) by a decrease in the number of samples (n) with identical multilocus genotype included in each distance class and for each analysis. The procedure is analogous for all 15 distance classes.
Genetic correlations between individuals can be summarized over a range of distance intervals in terms of a multilocus estimate of coancestry (Cockerham, 1969) or kinship (Barbujani, 1987). The advantage of genetic structure statistics such as the kinship coefficient is that they have a well-developed foundation in population genetic theory and provide a natural means of combining data over alleles at a locus and over loci (Heywood, 1991).
Following the methods of Loiselle et al (1995) and Burke et al (2000), we estimated the coancestry (fij) of all possible pairs of individuals within each population from their multilocus genotypes; fij measures the correlation in the frequencies of homologous alleles at each locus for each pair of mapped ramets (Cockerham, 1969) as

where pi and pj are the frequencies of homologous alleles of i, j pairs of mapped individuals, with the population sample allele frequency p̄ and k, the total number of possible pairwise connections located a discrete number of map units apart and N is the total number of samples used in each analysis. Mean values of fij were obtained for discrete distance intervals (1 m in all four plots, minimal distance 2 m, maximal distance 16 m) by averaging over all pairs of sampling points located within that interval as ∑pi(1 - pi). To obtain a multilocus measure of spatial genetic structure, the results were combined over loci by weighting each locus by its expected heterozygosity (He).
To assess statistical significance, fij values were compared to 95% confidence envelopes generated under the null hypothesis of no spatial genetic structure. Specifically, included samples (depending on the analysed clone structure (a)–(c)) were drawn at random with replacement and assigned to occupied map locations within each population. This procedure was repeated 399 times, with the observed fij representing the 400th statistic in each distance class. For a given distance class, fij is significantly different from zero at P<0.05 if the observed value falls above or below 95% of these statistics. When fij=0, there is no significant correlation among individuals at the spatial scale of interest; when fij>0, individuals in a given distance class are more closely related than expected by chance; and when fij<0, individuals within a given distance class are less related than expected by chance. It has been suggested that each distance class should contain at least 30, preferably >60 pairwise comparison for reliable estimates (Doligez and Joly, 1997; Epperson and Li, 1997). In the present work, each distance class contained >160 pairwise comparisons (mean=772±44), and hence estimates seem to be sufficiently reliable. Calculations were performed using programs developed by J Nason (University of Iowa). For fij we used FijAnal version 2.1 and for the bootstrap estimates BS_fij version 2.1. Both programs can be downloaded from the site http://www.nceas.ucsb.edu/papers/geneflow/software/index.html.
Results
The definition of joins as generated by the three different data sets that were analysed with autocorrelation on multilocus genotypes are presented in Figure 2. Each of these data sets represents the genetic neighbourhood of one specific level of organization of a clonal plant. The neighbourhood of a single unit (≈ramet) is most closely represented by the full data set including all original sampling points (Figure 2a). The neighbourhood of clone fragments (spatially independent aggregations of units) is represented by a reduced data set with only one sample per fragment and the coordinates moved to the centre. Finally, the neighbourhood of the genetic individual is represented by the data set that includes only one sampling point (eg centre point of the largest fragment) per genet.
All autocorrelation values were significantly higher than expected from a random pattern over short distances both for the Falkenstein and Maasholm plots (Figure 3). As expected, the absolute values for fij were highest when all samples were included in the analysis (Figure 3a). Here the aggregation of units with identical genotype through clonal expansion leads to high average fij values. The values decreased sharply with the stepwise decomposition of the clonal structure, excluding first joins within clone fragments, and then between any identical clone members (left to right Figure 3(a)–(c)). Within the shortest distance class (2 m), all fij were significantly positively correlated, but their absolute values varied between replicated plots both within and among populations (Table 1). It has been proposed that the x-intercept can be considered a measure of the spatial scale of autocorrelation (Upton and Fingleton, 1985; Epperson and Li, 1997). Likewise, the intercept with the confidence envelopes should provide a conservative estimate of the spatial scale with significant autocorrelation. The intercept of positive autocorrelation with the upper confidence limit decreased from 5 m in Falkenstein and 4 m in Maasholm to 2 m in both sites (Table 1) with the progressive exclusion of joins between identical genotypes. While for a single unit, the neighbourhood of up to 6 m radius consisted of close relatives (Figure 3a), for fragments (Figure 3b) and whole genets (Figure 3c) only the immediate neighbourhood was close kin. The plot pairs from each population showed similar values for the maximum distance of significant fij, but varied greatly in absolute values of fij 3 and Table 1).
Z. marina (eelgrass) autocorrelation of coancestry (fij) performed on genotypic data (a) including all samples, (b) including centre points of all fragments and (c) including center point of largest fragment for two plots (plot 1 open circles; plot 2 closed circles) in each of two populations (Falkenstein and Maasholm). Lines give 95% confidence envelopes around the null hypothesis fi=0 for plot 1 (solid) and plot 2 (dotted) in each population. Note that the scale of all axes is indicated only along the periphery, for reasons of clarity.
Discussion
Autocorrelation of microsatellite data on a fine-scale spatial grid showed that local genetic patterns in two Z. marina populations on the Baltic Coast are nonrandom at different levels of clonal structure. The significant positive autocorrelation for the data set representing only one individual of each clone (Figure 2c) revealed kinship structure beyond the spatial aggregation of ramets belonging to identical genotypes, suggesting limited gene flow in Z. marina meadows.
We are aware of only two other autocorrelation studies, that have explicitly considered the fact that individual clones can cover larger areas. First, in a study of allozyme polymorphism in a stand of Quercus chrysolepsis, Montalvo et al (1997) found that compared to an analysis including all possible joins (clonal structure (a) Table 1), significant positive autocorrelation of coancestry over the shortest distance class (2 m) decreased after excluding joins between clone mates (clonal structure (c) Table 1). Since absolute values were still substantially higher than expected for full and half-sib progeny, they assumed that a large amount of the genetic structure, which occurs over short distances, is due to clonal growth and might have been caused by scoring errors and/or somatic mutations. In addition, they report five cases in which two clones separated by >4 m within a plot share a common genotype. It is unlikely that the resolution of the chosen markers was not high enough to separate these common genotypes into different clones, because overall the probability for chance encounters was low (<0.01). Alternatively, the five cases reported may represent spatially independent clusters of one clone (structure (b) Table 1). Including these identical multilocus genotypes, as different clones in the analysis, will inflate autocorrelation estimates and may have been responsible for the very high coancestry values observed in their study. Second, in a study of the clonal plant Z. marina (eelgrass), Reusch et al (1999b) used standard deviate autocorrelation of microsatellite allele frequencies to compare a full analysis, including all samples (clonal structure (a) Table 1), with an analysis on a reduced data set, excluding joins within genets (clonal structure (c) Table 1). They found no significant autocorrelation over short distances when considering the spatial spread of genets and concluded that clonal growth is responsible for positive autocorrelation. The size of the sampled area (20 m × 80 m) was chosen according to estimates by Ruckelshaus (1996) for neighbourhood areas of c. 20–25 m (525 m2). For Z. marina, direct measurements of seed (Orth et al, 1994) and seed and pollen (Ruckelshaus, 1996) movement have shown that dispersal distances are no more than a few meters. Short dispersal distances of propagules are widespread among species of the marine coastal habitat despite strong water movements (Denny and Shibata, 1989; Engel et al, 1999). In the light of these empirical studies, the lack of positive autocorrelation over short distances in Z. marina was unexpected.
If the neighbourhood area was smaller in the Baltic than the 20–25 m estimated by Ruckelshaus (1996) for Pacific populations, then the scale of sampling in the study of Reusch et al (1999b) that had intended to cover four neighbourhood areas based on the limited information available at that time might have been too coarse to capture kinship structure. This is why the scale and intensity of sampling has been significantly increased in the present study.
Z. marina clones show spatial fragmentation (clone structure (b) Figure 2 and Table 1). Spatially separated groups of trees with identical genotype also indicated such a structure to be present in Quercus chrysolepsis (Montalvo et al, 1997). In the latter study, it was probably responsible for values of coancestry too high to be explained solely by limited dispersal. Spatial autocorrelation representing the clones (Figure 2c) requires the choice of only one sample per genotype, which most simply could be defined as the centre point of a clone. However, in the case of several clone fragments (Figure 2b) more than one centre point can be defined. In this study, we chose the centre point of the largest fragment because this fragment is expected to lay on average most closely to the origin of initial recruitment of a given clone. Analysis with the centre point of the smallest or a random fragment of each clone only slightly affected absolute values with no significant change in the results.
In the absence of inbreeding, the expected value of fij for full and half-sib progeny is 0.25 and 0.125, respectively (Queller and Goodnight, 1989). If we assume linear generations without backcrossing and low levels of inbreeding (as is known for Z. marina (Ruckelshaus, 1995)), then fij≈(0.5)n with n=number of generations. This yields an estimated maximum number of generations necessary to reach the observed significant fij values for the clone neighbourhood (Figure 3c, Table 1) of between four and six generations. This is most probably an overestimate of the generations needed to establish such a neighbourhood because Z. marina is self-compatible (de Cock, 1980) and backcrosses can be expected. Exact values are speculations, but the conservative rough estimates indicate that the immediate neighbourhood of a target clone is surprisingly young. In northern latitudes, turnover seems to be much lower as some clones from the northern Baltic Sea were estimated to be more than 1000 years old (Reusch et al, 1999a).
In the context of other studies on coancestry it seems, however, that absolute values can vary greatly among clonal plant species. Our values from the analysis including all samples range from 0.028 to 0.161 for the 2 m interval (Table 1). For the same distance, autocorrelation values from Louisiana iris hybrid populations showed a range of ≈0–0.2 (Burke et al, 2000) and for populations of canyon life oak ≈0.38–0.42 and 0.25 excluding multiple samples per genet (Montalvo et al, 1997). For the marine environment, Coyer has reported significant coancestry values of 0.060–0.092 for Z. noltii (Jim Coyer, unpublished data) at the 2 m scale and JL Olsen reported significant coancestry of 0.25 for Ascophyllum sp on a scale of 40 cm–1 m (Jeanine L Olsen, unpublished data). Both studies correspond to kinship among unique genotypes with no confounding clonal structure and their values are relatively high compared to the range of 0.009–0.015, excluding joins within genets, from this study (Table 1).
Dispersal distances for seed and pollen in Z. marina were found to be no more than a few meters (Orth et al, 1994; Ruckelshaus, 1996). In the sampled plots, we found significant kinship structure only within 2–4 m from a target individual, which seems to be in line with the empirical data. However, these figures could underestimate the neighbourhood area for eelgrass because the size of the panmictic breeding unit may be influenced by several factors. (i) We took the confidence limit intercept as threshold for both the absolute values of fij and the maximum distance with significant kinship structure. For the maximum distance, this threshold may be too conservative (Upton and Fingleton, 1985; Epperson and Li, 1997). Taking the x-intercept as a threshold instead would yield distances of 6–10 m. On the other hand, values within confidence limits should be interpreted with caution because they lay within the boundaries of random variation. Using standard normal deviate for spatial autocorrelation of five allozyme loci in Z. marina, Ruckelshaus (1998) used the x-intercept and estimated patch sizes of between 80 m × 80 m and 64 m × 64 m. This seems very large compared to the values from this study. (ii) To explore the clone level, the coordinates of the original sampling points were moved to the centre, which slightly reduced the physical distance to neighbouring points in the pairwise comparison. (iii) All clones within each of the 256 m2 plots were found to be in Hardy–Weinberg equilibrium, which indicates that the scale of panmixis may be larger than estimated from the maximum distance with significant coancestry.
Autocorrelation data from within-plant populations are complementary to studies of genetic differentiation between populations, often quantified as standardized allelic variance Fst. While autocorrelation analysis capture the left end of a dispersal–frequency vs distance function, that is the typical dispersal events, populations connectivity is mainly determined by occasional, rare long-distance dispersal events (Higgins and Richardson, 1999). There has been much debate on occasional dispersal of both seed and pollen through rafting shoots (Ruckelshaus, 1998). Although most observations of this process are anecdotal (but see Reusch, 2002), it is well possible that rafting of seed-bearing shoots is contributing to the local gene pool, influencing the size of the genetic neighbourhood through long-range dispersal. Even when taking the above-mentioned points into consideration, an assumed neighbourhood size of 525 m2 (Ruckelshaus, 1996) seems to overestimate the size of the panmictic breeding unit at least for the observed Baltic Sea populations of this study. For a more thorough understanding of both short- and long-range dispersal it would be desirable to be able to distinguish between the contributions of pollen and seeds to the local genetic structure. This may be possible in the near future with the establishment of maternal markers.
Another question is whether genet density within local populations reflects the initial colonizing cohort and its subsequent survivorship (initial seedling recruitment) or a continuous recruitment of genets (repeated seedling recruitment) (Eriksson, 1993). Still very little is known about recruitment patterns in Z. marina populations, and seagrass species in general. Recruitment through seedlings in the dense meadow is considered a rare event (Robertson and Mann, 1984; Olesen and Sand-Jensen, 1994a, 1994b, and personal observation). Although quantitative data are lacking for our study site, it is possible that seedling recruitment regularly occurs during the lifespan of clones (Reusch et al, 1999a). In general, for long-lived organisms such as clonal plants, assuming restricted dispersal, populations will have exceedingly long memories of initial colonization patterns and subsequent disturbance events (Heywood, 1991). If seedling recruitment is extremely low (low turnover) then this ‘memorizing effect’ should reduce kinship structuring and possibly cancel out significant autocorrelation signals. Since we find significant positive autocorrelation over short distances, we would argue that, although rare, continuous seedling recruitment is contributing to the local gene pool. Competition for space seems to be another important mechanism shaping mainly the size distribution of clones in eelgrass meadows. There is evidence that the more heterozygous clones are able to outcompete their relatively inbred neighbours (Hämmerli and Reusch, 2003).
One of the consequences of clonal growth is increasing between-ramet selfing (geitonogamy) with increasing distance of flowering shoots from their outcrossing neighbourhood. Our data show that as a direct consequence of kinship clusters, outcrossing between related individuals (biparental inbreeding) may augment the effects of geitonogamy. Both, geitonogamy (Handel, 1985; Eckert, 2000; Reusch, 2001) and biparental inbreeding, (Price and Waser, 1979; Levin, 1989; Fenster, 1991; Waser and Price, 1994) have been shown to result in reduced offspring fitness. Hence for pollen of a single flowering shoot within a clone, the mating landscape with increasing distance to its outcrossing neighbourhood is a continuum of between-ramet selfing (geitonogamy), biparental inbreeding and full outcrossing. The decomposition of the clonal structure (Figure 3, left-right) can be viewed as a simulation of reduced physical distance to the full outcrossing neighbourhood with an increase of chances for successful fertilization. If this effect translates into selection pressure for outcrossing in the natural environment, then the tendency for spatial disintegration of larger clones into fragment clusters may be adaptive in Z. marina. This could be an interesting starting point for future experiments.
The present study has shown that the stepwise decomposition of clonal structure reduces the positive spatial autocorrelation both in absolute terms and in terms of the maximum distance with significant deviation from random expectations. Even with this reduction, considering the spatial spread of genetic individuals, clones grow in a neighbourhood of significant kinship structure. Hence, spatial autocorrelation crucially depends on the scale of sampling (representation of dispersal distances) and in the case of clonal plants, on the sampling scheme (representation of clonal structure). It will be desirable for future studies to have direct measurements of recruitment patterns in Z. marina meadows to obtain deeper insights into the connection between pattern and process.
References
Barbujani B (1987). Autocorrelation of gene frequencies under isolation by distance. Genetics 117: 772–782.
Biosystems A (1998). Genotyper. PE Biosystems: Foster City.
Biosystems A (2001). Genotyper. PE Biosystems: Foster City.
Bradshaw AD (1972). Some of the evolutionary consequences of being a plant. In: Dobzhansky, Theodosius, Heiht MK, Steeve WC (eds), Evolutionary Biology, Plenum Press: New York. pp 25–47.
Burke JM, Bulger MR, Wesselingh RA, Arnold ML (2000). Frequency and spatial patterning of clonal reproduction in Louisiana iris hybrid populations. Evolution 54: 137–144.
Callaghan TV, Carlsson BA, Jonsdottir IS, Svensson BM, Jonasson S (1992). Clonal plants and environmental change: introduction to the proceedings and summary. Oikos 63: 341–347.
Caujape-Castells J, Pedrola-Monfort J (1997). Space–time patterns of genetic structure within a stand of Androcymbium Gramineum (Cav.) Mcbride (Colchicaceae). Heredity 79: 341–349.
Caujape-Castells J, Pedrola-Monfort J, Membrives N (1999). Contrasting patterns of genetic structure in the South African species Androcymbium bellum, A. guttatum and A. pulchrum (Colchicaceae). Bioch Syst Ecol 27: 591–605.
Cockerham CC (1969). Variance of gene frequencies. Evolution 23: 72–84.
De Cock A.W.A.M (1980). Flowering pollination and fruiting in Zostera marina L. Aquat Bot 9: 201–220.
den Hartog C (1970). The seagrasses of the wold. Verhandlingen Koninglijk Nederlandse Akademie Wetenschapen Afdeling Natuurkunde 59: 1–275.
Denny MW, Shibata MF (1989). Consequences of surf-zone turbulence for settlement and external fertilization. Am Nat 134: 859–889.
Doligez A, Joly HI (1997). Genetic diversity and spatial structure within a natural stand of a tropical forest tree species, Carapa procera (Meliaceae), in French Guiana. Heredity 79: 72–82.
Eckert CG (2000). Contributions of autogamy and geitonogamy to self-fertilization in a mass-flowering, clonal plant. Ecology 81: 532–542.
Engel CR, Wattier R, Destombe C, Valero M (1999). Performance of non-motile male gametes in the sea: analysis of paternity and fertilization success in a natural population of a red seaweed. Gracilaria gracilis. Proc Rl Soc B 266: 1879–1886.
Epperson BK (1993). Recent advantages in correlation studies of spatial patterns of genetic variation. In: Hecht MK, MacIntyre RJ Clegg MT (eds), Evolutionary Biology, Plenum Press: New York, pp 95–155.
Epperson BK, Li T-Q (1997). Gene dispersal and spatial genetic structure. Evolution 51: 672–681.
Eriksson O (1993). Dynamics of genets in clonal plants. TREE 8: 313–316.
Fenster CB (1991). Gene flow in Chamaecrista fasciculata. II. Gene establishment. Evolution 45: 410–422.
Hämmerli A, Reusch TBH (2003). Inbreeding depression influences genet size distribution in a marine angiosperm. Mol Ecol 12: 619–629.
Handel SN (1985). The intrusion of clonal growth patterns on plant breeding systems. Am Nat 125: 367–384.
Harper JL (1977). Population Biology of Plants. Academic Press: New York.
Heywood JS (1991). Spatial analysis of genetic variation in plant populations. Ann Rev Ecol Syst 22: 335–355.
Higgins SI, Richardson DM (1999). Predicting plant migration rates in a changing world: the role of long-distance dispersal. Am Nat 153: 464–475.
Kimura M, Weiss GH (1964). The stepping stone model of population structure and the decrease of genetic correlation with distance. Genetics 49: 561–567.
Klimes L, Klimesova J, Hendriks R, van Groenendael J (1997). Clonal plant architecture: a comparative analysis form and function. In: de Kroon and H, van Groenendael J (eds), The Ecology and Evolution of Clonal Plants, Backhuys Publishers: Leiden, The Netherlands, pp. 1–29.
Legendre P (1993). Spatial autocorrelation: Trouble or new paradigm? Ecology 74: 1659–1673.
Levin DA (1989). Proximity-dependent cross-compatibility in Phlox. Evolution 43: 1114–1116.
Levin DA, Kerster HW (1971). Neighbourhood structure in plants under diverse reprocuctive methods. Am Nat 105: 345–354.
Loiselle BA, Sork VL, Nason J, Graham C (1995). Spatial genetic structure of a tropical understory shrub, Psychotria officinalis (Rubiaceae). Am J Bot 82: 1420–1425.
Major A, Odor P (1999). Genet composition of Diphasiastrum complanatum in Western Hungary: a case study. Am Fern J 89: 106–123.
Marahrens M (1995). Biologisch-ökologische Untersuchungen der Windwatten des NSG ‘Oehe-Schleimünde’ unter dem Aspekt ihrer Verfügbarkeit als Nahrungsraum für die im Schutzgebiet brütenden und rastenden Seevögel. In: Schlussbericht Verein Jordsand (eds), Institut für Naturschutz- und Umweltschutzforschung (INUF) des Verein Jordsand.
Math Works I (2000). MATLAB. The Math Works: Natick.
Maynard Smith J (1976). The Evolution of Sex. Cambridge University Press: Cambridge.
Montalvo AM, Conard SG, Conkle MT, Hodgskiss PD (1997). Population structure, genetic diversity, and clone formation in Quercus shrysolepsis (Fagaceae). Am J Bot 84: 1553–1564.
Nakamura RR (1980). Plant kin selection. Evol Theor 5: 117.
Olesen B, Sand-Jensen K (1994a). Demography of shallow eelgrass (Zostera marina) populations – shoot dynamics and biomass development. J Ecol 80: 379–390.
Olesen B, Sand-Jensen K (1994b). Patch dynamics of eelgrass Zostera marina. Mar Ecol Prog Ser 106: 147–156.
Orth RJ, Luckenback M, Moore KA (1994). Seed dispersal in a marine macrophyte: implications for colonization and restoration. Ecology 75: 1927–1939.
Parks JC, Werth, CR (1993). A study of spatial features of clones in a population of bracken fern, Pteridium aquilinum (Dennstaedtiaceae). Am J Bot 80: 537–544.
Price MV, Waser NM (1979). Pollen dispersal and optimal outcrossing in Delphinium nelsoni. Nature 277: 294–297.
Queller DC, Goodnight KF (1989). Estimating relatedness using genetic markers. Evolution 43: 258–275.
Reusch TBH (2001). Fitness-consequences of geitonogamous selfing in a clonal marine angiosperm (Zostera marina). J Evol Biol 14: 129–138.
Reusch TBH (2002). Microsatellites reveal high population connectivity in eelgrass (Zostera marina) in two contrasting coastal areas. Limnol and Ooanogr 47: 78–85.
Reusch TBH, Bostrom C, Stam WT, Olsen JL (1999a). An ancient eelgrass clone in the Baltic. Mar Ecol Prog Ser 183: 301–304.
Reusch TBH, Hukriede W, Stam WT, Olsen JL (1999b). Differentiating between clonal growth and limited gene flow using spatial autocorrelation of microsatellites. Heredity 83: 120–126.
Reusch TBH, Stam WT, Olsen JL (2000). A microsatellite-based estimation of clonal diversity and population subdivision in Zostera marina, a marine flowering plant. Mol Ecol 9: 127–140.
Robertson AI, Mann KH (1984). Disturbance by ice and life-history adaptations of the seagrass Zostera marina. Mar Biol 80: 131–141.
Ruckelshaus MH (1995). Estimates of outcrossing rates and of inbreeding depression in a population of the marine angiosperm, Zostera marina. Mar Biol 123: 583–593.
Ruckelshaus MH (1996). Estimation of genetic neighborhood parameters from pollen and seed dispersal in the marine angiosperm Zostera Marina L. Evolution 50: 856–864.
Ruckelshaus MH (1998). Spatial scale of genetic structure and an indirect estimate of gene flow in eelgrass, Zostera marina. Evolution 52: 330–343.
Smouse PE, Peakall R (1999). Spatial autocorrelation analysis of individual multiallele and multilocus genetic structure. Heredity 82: 561–573.
Sokal RR, Oden NL (1978a). Spatial autocorrelation in biology. 2. Some biological implications and four applications of evolutionary and ecological interest. Biol J Linn Soc 10: 229–249.
Sokal RR, Oden NL (1978b). Spatial autocorrelation in biology. 1. Methodology. Biol J Linn Soc 10: 199–228.
Suzuki JI, Herben T, Krahulec F, Hara T (1999). Size and spatial pattern of Festuca rubra genets in a mountain grassland: its relevance to genet establishment and dynamics. J Ecol 87: 942–954.
Sydes MA, Peakall R (1998). Extensive clonality in the endangered shrub Haloragodendron lucasii (Haloragaceae) revealed by allozymes and RAPDs. Mol Ecol 7: 87–93.
Upton GJG, Fingleton B (1985). Point Pattern and Quantitative Data,Wiley: New York.
van Groenendael J, de Kroon H (1990). Clonal Growth in Plants: Regulation and function. SPB Academic: The Hague.
Waser NM, Price MV (1994). Crossing-distance effects in Delphinium nelsonii: outbreeding and inbreeding depression in progeny fitness. Evolution 48: 842–852.
Watson MA, Casper B (1984). Morphogenetic constraints on patterns of carbon distribution in plants. Ann Rev Ecol Syst 15: 233–258.
Acknowledgements
We thank Anneli Ehlers and Sascha Romatzki for helping in the field, Silke Carstensen and Catha Schmuck for help with the fragment analysis, Annelis Lüscher, John Thompson and two anonymous referees for comments on an earlier draft of this manuscript, Jérôme Goudet for discussion, Jeanine L Olsen and Jim Coyer for permission to cite unpublished data and Manuel Kägi for statistical advice.
This work has been funded by a grant to TR from the Deutsche Forschungsgemeinschaft (DFG). Grant No. 1108/3-1.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hämmerli, A., Reusch, T. Genetic neighbourhood of clone structures in eelgrass meadows quantified by spatial autocorrelation of microsatellite markers. Heredity 91, 448–455 (2003). https://doi.org/10.1038/sj.hdy.6800310
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/sj.hdy.6800310
Keywords
This article is cited by
-
Seed Production Patterns in Zostera marina: Effects of Patch Size and Landscape Configuration
Estuaries and Coasts (2017)
-
Genetic variability and population structure in a collection of inbred lines derived from a core germplasm of castor
Journal of Plant Biochemistry and Biotechnology (2017)
-
Fine-scale patterns of genetic variation in a widespread clonal seagrass species
Marine Biology (2016)
-
Fine-scale spatial genetic structure and clonal distribution of the cold-water coral Lophelia pertusa
Coral Reefs (2012)
-
Microscale genetic differentiation in a sessile invertebrate with cloned larvae: investigating the role of polyembryony
Marine Biology (2007)