Main

For a confocal unstable resonator consisting of a large concave mirror and a small convex feedback mirror sharing a common focus, the rays spill over the small mirror so that its size and shape define the output aperture (Fig. 1, insets); the other mirror is so large that its size and shape are irrelevant. The properties of an unstable resonator are determined by the round- trip magnification M and the (equivalent) Fresnel number N of the resonator: N≡(M−1)a2/2λL, where λ is the optical wavelength, 2a is the size of the small mirror, and L is the cavity length1. The existence of a round-trip magnification M is characteristic for unstable resonators, as stable resonators lack such magnification. The value of M determines the round-trip spill-over loss around the small mirror, and N controls the size of the smallest details in the transverse mode profile as determined by diffraction. In an unstable-cavity laser, the losses are compensated by the gain provided by the laser medium.

Figure 1: Calculated lowest-loss eigenmode of an unstable resonator with a triangular mirror.
figure 1

Left inset, a three-dimensional view; right inset, a side view. M=1.5, N=10.5. The intensity distribution |u|2 on the small mirror is shown: white, high; red, medium; blue, low. Bottom, magnification of the centre part, with colour coding adjusted to exploit the full dynamical range.

Full size image

Free-space propagation of the optical field is described by the Huygens–Fresnel integral1, and cavity eigenmodes u(x,y) are defined by the requirement that, after one round trip, the field profile remains unchanged apart from a complex multiplier (the eigenvalue of the mode). We have calculated the mode patterns for a range of different aperture shapes, concentrating particularly on regular polygons and rhomboids. This calculation is numerically very demanding, so we used a non-orthogonal grid2 to increase efficiency. For square or circular apertures, the diffraction problem can be reduced to a one-dimensional calculation, with the mode patterns for the square factorizing into x and y components.

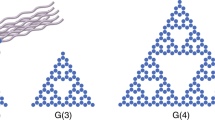
A typical modal intensity distribution for triangular aperturing is shown in Fig. 1. Smaller and smaller triangles keep appearing as the mode pattern is repeatedly magnified. This shows the self-similar nature of the mode, which continues down to the diffraction limit of approximately a/4N. On even smaller scales, further magnification does not reveal further substructure (Fig. 1, bottom). In the asymptotic limit λ↓0 (N→∞), the diffractive spreading becomes negligible, leading to an ideal fractal. Large-N resonators are feasible (for example, N=14 has already been realized in ref. 3).

The origin of the self-similarity can be understood intuitively: the existence of the round-trip magnification M means that the eigenmode must consist of (de)magnified copies of itself. Note that the hermite–gaussian modes of stable resonators are not self-similar because the round-trip magnification is absent.

A characteristic property of fractals is their non-integer fractal dimension Df (refs 4,5). We found that an accurate determination of Df for two-dimensional modes (as in Fig. 1) would require calculations at much higher N than considered here, and hence computational resources beyond those available; in earlier calculations6 for one-dimensional resonators with N=103, we found that Df was 1.6±0.1.

It has been shown that a tetraedical stacking of four reflecting spheres represents a chaotically scattering system with inherent fractal properties7. Our results help to explain this: light rays repeatedly scattering in the inner chamber of the tetraedical stacking undergo geometrical magnification owing to the reflecting spheres, just as in our unstable resonator. Coincidentally, the ‘aperture’ in ref. 7 is approximately triangular, like our aperture in Fig. 1, leading to similar patterns. The self-similar aspect seems to be a useful unifying feature of optical-pattern generation, providing insight into chaotic scattering7 and transverse nonlinear optics8. In the latter case, there is competition between bulk nonlinear behaviour and boundary-imposed linear diffraction as pattern-generating mechanisms.