Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

World Year of Physics

A direct test of E=mc2

Nature volume 438, pages 1096–1097 (2005)Cite this article

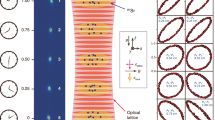
Abstract

One of the most striking predictions of Einstein's special theory of relativity is also perhaps the best known formula in all of science: E=mc2. If this equation were found to be even slightly incorrect, the impact would be enormous — given the degree to which special relativity is woven into the theoretical fabric of modern physics and into everyday applications such as global positioning systems. Here we test this mass–energy relationship directly by combining very accurate measurements of atomic-mass difference, Δm, and of γ-ray wavelengths to determine E, the nuclear binding energy, for isotopes of silicon and sulphur. Einstein's relationship is separately confirmed in two tests, which yield a combined result of 1−Δmc2/E=(−1.4±4.4)×10−7, indicating that it holds to a level of at least 0.00004%. To our knowledge, this is the most precise direct test of the famous equation yet described.

Your institute does not have access to this article

Relevant articles

Open Access articles citing this article.

Access options

Buy article

Get time limited or full article access on ReadCube.

$32.00

Buy

All prices are NET prices.

Figure 1: Typical data for testing E=Δmc2.

References

  1. Mohr, P. J. & Taylor, B. N. Rev. Mod. Phys. 77, 1–107 (2005).

    ADS  CAS  Article  Google Scholar 

  2. Kessler, E. G. et al. Phys. Lett. A 255, 221–229 (1999).

    ADS  CAS  Article  Google Scholar 

  3. Kessler, E. G. et al. Nucl. Instrum. Meth. Phys. Res. A 457, 187–202 (2001).

    ADS  CAS  Article  Google Scholar 

  4. Dewey, M. S. et al. Preprint nucl-ex/0507011 at http://arxiv.org (2005).

  5. Rainville, S., Thompson, J. K. & Pritchard, D. E. Science 303, 334–338 (2004).

    ADS  CAS  Article  Google Scholar 

  6. Audi, G., Wapstra, A. H. & Thibault, C. Nucl. Phys. A 729, 337–676 (2003).

    ADS  Article  Google Scholar 

  7. Thompson, J. K., Rainville, S. & Pritchard, D. E. Nature 430, 58–61 (2004).

    ADS  CAS  Article  Google Scholar 

  8. NIST Chemistry WebBook, NIST Standard Reference Database Number 69 (eds Linstrom, P. J. & Mallard, W. G.) (National Institute of Standards and Technology, Gaithersburg, Maryland, 2003).

  9. Chase, M. W. J. Phys. Chem. Ref. Data Monogr. 9, 1–1951 (1998).

    Google Scholar 

  10. Greene, G. L., Dewey, M. S., Kessler, E. G. & Fischbach, E. Phys. Rev. D 44, R2216–R2219 (1991).

    ADS  CAS  Article  Google Scholar 

Download references

Author information

Author notes

  1. Hans G. Börner

    Present address: Institut Laue-Langevin, Grenoble, 38042, Cedex, France

  2. Simon Rainville

    Present address: Département de Physique, Université Laval, Québec, G1K 7P4, Canada

Authors and Affiliations

  1. Department of Physics, Research Laboratory of Electronics, MIT–Harvard Center for Ultracold Atoms, Massachusetts Institute of Technology, Cambridge, 02139, Massachusetts, USA

    Simon Rainville, James K. Thompson & David E. Pritchard

  2. Department of Physics, Florida State University, Tallahassee, 32306-4350, Florida, USA

    Edmund G. Myers

  3. Department of Chemistry, The Physical and Theoretical Chemistry Laboratory, South Parks Road, Oxford, OX1 3QZ, UK

    John M. Brown

  4. National Institute of Standards and Technology, Gaithersburg, 20899, Maryland, USA

    Maynard S. Dewey, Ernest G. Kessler Jr & Richard D. Deslattes

  5. Institut Laue-Langevin, Grenoble, 38042, Cedex, France

    Michael Jentschel & Paolo Mutti

Authors
  1. Simon Rainville
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. James K. Thompson
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Edmund G. Myers
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. John M. Brown
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Maynard S. Dewey
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Ernest G. Kessler Jr
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Richard D. Deslattes
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Hans G. Börner
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Michael Jentschel
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Paolo Mutti
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. David E. Pritchard
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Simon Rainville.

Supplementary information

Rights and permissions

Reprints and Permissions

About this article

Cite this article

Rainville, S., Thompson, J., Myers, E. et al. A direct test of E=mc2. Nature 438, 1096–1097 (2005). https://doi.org/10.1038/4381096a

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/4381096a

Further reading

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing