Abstract
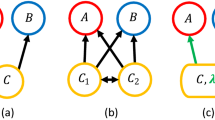
Most species live in species-rich food webs; yet, for a century, most mathematical models for population dynamics have included only one or two species1,2,3. We ask whether such models are relevant to the real world. Two-species population models of an interacting consumer and resource collapse to one-species dynamics when recruitment to the resource population is unrelated to resource abundance, thereby weakening the coupling between consumer and resource4,5,6. We predict that, in nature, generalist consumers that feed on many species should similarly show one-species dynamics. We test this prediction using cyclic populations, in which it is easier to infer underlying mechanisms7, and which are widespread in nature8. Here we show that one-species cycles can be distinguished from consumer–resource cycles by their periods. We then analyse a large number of time series from cyclic populations in nature and show that almost all cycling, generalist consumers examined have periods that are consistent with one-species dynamics. Thus generalist consumers indeed behave as if they were one-species populations, and a one-species model is a valid representation for generalist population dynamics in many-species food webs.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

Similar content being viewed by others
References
Lotka, A. J. Elements of Physical Biology (Dover, New York, 1925, reprinted 1956)
Hassell, M. P., Lawton, J. H. & May, R. M. Patterns of dynamical behaviour in single species populations. J. Anim. Ecol. 45, 471–486 (1976)
Gurney, W. S. C. & Nisbet, R. M. Ecological Dynamics (Oxford Univ. Press, New York, 1998)
McCauley, E., Nisbet, R. M., De Roos, A. M., Murdoch, W. W. & Gurney, W. S. C. Structured population models of herbivorous zooplankton. Ecol. Monogr. 66, 479–501 (1996)
Persson, L. et al. Ontogenetic scaling of foraging rates and the dynamics of a size-structured consumer-resource model. Theor. Popul. Biol. 54, 270–293 (1998)
Briggs, C. J., Nisbet, R. M. & Murdoch, W. W. Host age-specific parasitoid gain, delayed-feedback, and multiple attractors in a host-parasitoid model. J. Math. Biol. 38, 317–345 (1999)
Kendall, B. E. et al. Why do populations cycle? A synthesis of statistical and mechanistic modeling approaches. Ecology 80, 1789–1805 (1999)
Kendall, B. E., Prendergast, J. & Bjornstad, O. N. The macroecology of population dynamics: taxonomic and biogeographic patterns in populations cycles. Ecol. Lett. 1, 160–164 (1998)
Stenseth, N. C., Falck, W., Bjornstad, O. N. & Krebs, C. J. Population regulation in snowshoe hare and Canadian lynx: Asymmetric food web configurations between hare and lynx. Proc. Natl Acad. Sci. USA 94, 5147–5152 (1997)
Bjornstad, O. N., Sait, S. M., Stenseth, N. C., Thompson, D. J. & Begon, M. The impact of specialized enemies on the dimensionality of host dynamics. Nature 409, 1001–1006 (2001)
Gurney, W. S. C. & Nisbet, R. M. Fluctuation periodicity, generation separation, and the expression of larval competition. Theor. Popul. Biol. 28, 150–180 (1985)
Jones, A. E., Nisbet, R. M., Gurney, W. S. C. & Blythe, S. P. Period to delay ratio near stability boundaries for systems with delayed feedback. Math. Anal. Appl. 135, 354–368 (1988)
Blythe, S. P., Nisbet, R. M. & Gurney, W. S. C. Instability and complex dynamical behaviour in population models with long time delays. Theor. Popul. Biol. 22, 147–176 (1982)
Higgins, K., Hastings, A. & Botsford, L. W. Density dependence and age structure: Nonlinear dynamics and population behaviour. Am. Nat. 149, 247–269 (1997)
Nisbet, R. M. & Bence, J. R. Alternative dynamic regimes for canopy-forming kelp: A variant on density-vague population regulation. Am. Nat. 134, 377–408 (1989)
Lauwerier, H. A. & Metz, J. A. J. Hopf bifurcation in host-parasitoid models. Inst. Math. Appl. J. Math. Appl. Med. Biol. 3, 191–210 (1986)
Nisbet, R. M. & Gurney, W. S. C. Modelling Fluctuating Populations (Wiley, New York, 1982)
NERC Centre for Population Biology, Imperial College The Global Population Dynamics Database, (NERC, Ascot 1999); available at http://www.sw.ic.ac.uk/cpb/cpb/gpdd.html
Finerty, J. P. The Population Ecology of Cycles in Small Mammals: Mathematical Theory and Biological Fact (Yale Univ. Press, New Haven, 1980)
Lindstrom, E. R. et al. Disease reveals the predator: Sarcoptic mange, red fox predation, and prey populations. Ecology 75, 1042–1049 (1994)
O'Donoghue, M., Boutin, S., Hofer, E. J. & Boonstra, R. in Ecosystem Dynamics of the Boreal Forest: the Kluane Project (eds Krebs, C. J., Boutin, S. & Boonstra, R.) 325–340 (Oxford Univ. Press, New York, 2001)
Bulmer, M. G. A statistical analysis of the 10-year cycle in Canada. J. Anim. Ecol. 43, 701–718 (1974)
Berryman, A. A. What causes population cycles of forest Lepidoptera? Trends Ecol. Evol. 11, 28–32 (1996)
Ginzburg, L. R. & Taneyhill, D. E. Population cycles of forest Lepidoptera: a maternal effect hypothesis. J. Anim. Ecol. 63, 79–92 (1994)
Thomson, D. J. Spectrum estimation and harmonic analysis. Proc. IEEE 70, 1055–1096 (1982)
Park, J., Lindberg, C. R. & Vernon, F. L. Multitaper spectral analysis of high-frequency spectrograms. J. Geophys. Res. 92, 12675–12684 (1987)
Lees, J. M. & Park, J. Multiple-taper spectral analysis: a stand-alone C-subroutine. Comput. Geosci. 21, 199–236 (1995)
Acknowledgements
We thank C. Godfray for permission to analyse time series from the Global Population Dynamics Database (GPDD). We thank J. Fryxell, B.K. Gilbert, S. Henke, P.J. Hudson, C.J. Krebs, L. Oksanen, B. Sanderson, S. Taylor and M. Tewes for discussions on particular taxa, and J.A.J. Metz for discussions of cycle periods. The research was supported by grants from the NSF and United States Department of Agriculture (USDA).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests
Rights and permissions
About this article
Cite this article
Murdoch, W., Kendall, B., Nisbet, R. et al. Single-species models for many-species food webs. Nature 417, 541–543 (2002). https://doi.org/10.1038/417541a
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/417541a
This article is cited by
-
Wavelet clustering analysis as a tool for characterizing community structure in the human microbiome
Scientific Reports (2023)
-
The regulating effect of growth plasticity on the dynamics of structured populations
Theoretical Ecology (2022)
-
Herbivore population dynamics in response to plant allocation strategies
Theoretical Ecology (2022)
-
Integrated sustainability policy assessment – an agent-based ecological-economic model
Journal of Evolutionary Economics (2022)
-
An updated perspective on spiders as generalist predators in biological control
Oecologia (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.