Abstract
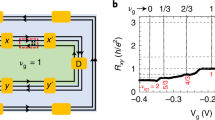
The discreteness of charge in units of e led Schottky in 1918 to predict that the electrical current in a vacuum tube fluctuates even if all spurious noise sources are eliminated carefully1. This phenomenon is now widely known as shot noise. In recent years, shot noise in mesoscopic conductors, where charge motion is quantum-coherent over distances comparable to the system size, has been studied extensively2,3,4,5. In those experiments, charge does not propagate as an isolated entity through free space, as for vacuum tubes, but is part of a degenerate and quantum-coherent Fermi sea of charges. It has been predicted that shot noise in mesoscopic conductors can disappear altogether when the system is tuned to a regime where electron motion becomes classically chaotic6. Here we experimentally verify this prediction by using chaotic cavities where the time that electrons dwell inside can be tuned7. Shot noise is present for large dwell times, where the electron motion through the cavity is ‘smeared’ by quantum scattering, and it disappears for short dwell times, when the motion becomes classically deterministic.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Schottky, W. Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern. Ann. Phys. (Leipz.) 57, 541–568 (1918).
Blanter, Y. M. & Büttiker, M. Shot noise in mesoscopic conductors. Phys. Rep. 336, 1–166 (2000).
Lesovik, G. B. Excess quantum noise in 2D ballistic point contacts. JETP Lett. 49, 592–594 (1989).
Reznikov, M., Heiblum, M., Shtrikman, H. & Mahalu, D. Temporal correlation of electrons: Suppression of shot noise in a ballistic quantum point contact. Phys. Rev. Lett. 75, 3340–3343 (1995).
Kumar, A., Saminadayar, L., Glattli, D. C., Jin, Y. & Etienne, B. Experimental test of the quantum shot noise reduction theory. Phys. Rev. Lett. 76, 2778–2781 (1996).
Agam, O., Aleiner, I. & Larkin, A. Shot noise in chaotic systems: Classical to quantum crossover. Phys. Rev. Lett. 85, 3153–3156 (2000).
Oberholzer, S. et al. Shot noise by quantum scattering in chaotic cavities. Phys. Rev. Lett. 86, 2114–2117 (2001).
Hartmann, C. A. Über die Bestimmung des elektrischen Elementarquantums aus dem Schroteffekt. Ann. Phys. (Leipz.) 65, 51–78 (1921).
Hull, A. W. & Williams, N. H. Determination of elementary charge e from measurements of the shot-effect. Phys. Rev. 25, 147–173 (1925).
Büttiker, M. Scattering theory of current and intensity noise correlations in conductors and wave guides. Phys. Rev. B 46, 12485–12507 (1992).
Beenakker, C. W. J. & van Houten, H. Semiclassical theory of shot noise and its suppression in a conductor with deterministic scattering. Phys. Rev. B 43, 12066–12069 (1992).
van Wees, B. J. et al. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 60, 848–851 (1988).
Wharam, D. A. et al. One-dimensional transport and the quantisation of the ballistic resistance. J. Phys. C 21, L209–L214 (1988).
Blanter, Y. M. & Sukhorukov, E. V. Semiclassical theory of conductance and noise in open chaotic cavities. Phys. Rev. Lett. 84, 1280–1283 (2000).
Jalabert, R. A., Pichard, J.-L. & Beenakker, C. W. J. Universal quantum signatures of chaos in ballistic transport. Europhys. Lett. 27, 255–2660 (1994).
Acknowledgements
We thank H. Büttiker and H. Thomas for discussions. This work was supported by the Swiss National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Oberholzer, S., Sukhorukov, E. & Schönenberger, C. Crossover between classical and quantum shot noise in chaotic cavities. Nature 415, 765–767 (2002). https://doi.org/10.1038/415765a
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/415765a
This article is cited by
-
Conductance fluctuations in high mobility monolayer graphene: Nonergodicity, lack of determinism and chaotic behavior
Scientific Reports (2016)
-
Integrable Aspects of Universal Quantum Transport in Chaotic Cavities
Constructive Approximation (2015)
-
Effect of magnetic field on shot noise in diffusive conductors and cascaded barriers
Journal of Computational Electronics (2008)
-
Shot noise in transport through quantum dots: Clean versus disordered samples
Journal of Computational Electronics (2007)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.