Abstract
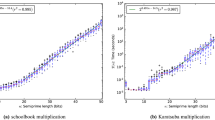
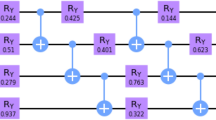
The number of steps any classical computer requires in order to find the prime factors of an l-digit integer N increases exponentially with l, at least using algorithms known at present1. Factoring large integers is therefore conjectured to be intractable classically, an observation underlying the security of widely used cryptographic codes1,2. Quantum computers3, however, could factor integers in only polynomial time, using Shor's quantum factoring algorithm4,5,6. Although important for the study of quantum computers7, experimental demonstration of this algorithm has proved elusive8,9,10. Here we report an implementation of the simplest instance of Shor's algorithm: factorization of N = 15 (whose prime factors are 3 and 5). We use seven spin-1/2 nuclei in a molecule as quantum bits11,12, which can be manipulated with room temperature liquid-state nuclear magnetic resonance techniques. This method of using nuclei to store quantum information is in principle scalable to systems containing many quantum bits13, but such scalability is not implied by the present work. The significance of our work lies in the demonstration of experimental and theoretical techniques for precise control and modelling of complex quantum computers. In particular, we present a simple, parameter-free but predictive model of decoherence effects14 in our system.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Knuth, D. E. The Art of Computer Programming Vol. 2, Seminumerical Algorithms (Addison-Wesley, Reading, Massachusetts, 1998).
Koblitz, N. A Course in Number Theory and Cryptography (Springer, New York, 1994).
Bennett, C. H. & DiVincenzo, D. P. Quantum information and computation. Nature 404, 247–255 (2000).
Shor, P. in Proc. 35th Annu. Symp. on the Foundations of Computer Science (ed. Goldwasser, S.) 124–134 (IEEE Computer Society Press, Los Alamitos, California, 1994).
Shor, P. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26, 1484–1509 (1997).
Ekert, A. & Jozsa, R. Quantum computation and Shor's factoring algorithm. Rev. Mod. Phys. 68(3), 733–753 (1996).
Beckman, D., Chari, A. N., Devabhaktuni, S. & Preskill, J. Efficient networks for quantum factoring. Phys. Rev. A 54, 1034–1063 (1996).
Jones, J. A. NMR quantum computation. Prog. NMR Spectrosc. 38, 325–360 (2001).
Vandersypen, L. M. K. et al. Experimental realization of an order-finding algorithm with an NMR quantum computer. Phys. Rev. Lett. 85, 5452–5455 (2000).
Knill, E., Laflamme, R., Martinez, R. & Tseng, C.-H. An algorithmic benchmark for quantum information processing. Nature 404, 368–370 (2000).
Gershenfeld, N. & Chuang, I. L. Bulk spin-resonance quantum computation. Science 275, 350–356 (1997).
Cory, D. G., Fahmy, A. F. & Havel, T. F. Ensemble quantum computing by NMR spectroscopy. Proc. Natl Acad. Sci. 94, 1634–1639 (1997).
Schulman, L. & Vazirani, U. in Proc. 31st ACM Symp. on Theory of Computing 322–329 (Association for Computing Machinery, New York, 1999).
Chuang, I. L., Laflamme, R., Shor, P. & Zurek, W. H. Quantum computers, factoring, and decoherence. Science 270, 1633–1635 (1995).
Freeman, R. Spin Choreography (Spektrum, Oxford, 1997).
Braunstein, S. L. et al. Separability of very noisy mixed states and implications for NMR quantum computing. Phys. Rev. Lett. 83, 1054–1057 (1999).
Schack, R. & Caves, C. M. Classical model for bulk-ensemble NMR quantum computation. Phys. Rev. A 60, 4354–4362 (1999).
Linden, N. & Popescu, S. Good dynamics versus bad kinematics: Is entanglement needed for quantum computation? Phys. Rev. Lett. 87, 047901 (2001).
Coppersmith, D. An Approximate Fourier Transform Useful in Quantum Factoring (IBM Res. Rep. RC19642, IBM T. J. Watson Research Centre, Yorktown Heights, New York, 1994).
Vold, R. L. & Vold, R. R. Nuclear magnetic relaxation in coupled spin systems. Prog. NMR Spectrosc. 12, 79–133 (1978).
Jeener, J. Superoperators in magnetic resonance. Adv. Magn. Reson. 10, 1–51 (1982).
Bloch, F. Nuclear induction. Phys. Rev. 70, 460–474 (1946).
Kraus, K. States, Effects, and Operations: Fundamental Notions of Quantum Theory (Springer, Berlin, 1983).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, Cambridge, 2000).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Vandersypen, L. M. K. et al. Implementation of a three-quantum-bit search algorithm. Appl. Phys. Lett. 76, 646–648 (2000).
Aho, A. V., Sethi, R. & Ullman, J. D. Compilers: Principles, Techniques and Tools (Addison-Wesley, Reading, Massachusetts, 1986).
Green, M., Mayne, N. & Stone, F. G. A. Chemistry of the metal carbonyls. Part XLVI. Perfluorobutadienyl iron, rhenium and manganese complexes. J. Chem. Soc. A 902–905 (1968).
Leung, D. W. et al. Efficient implementation of selective recoupling in heteronuclear spin systems using Hadamard matrices. Phys. Rev. A 61, 042310 (2000).
Acknowledgements
We thank X. Zhou and J. Preskill for discussions, J. Smolin for the use of his IBM workstation, D. Miller for help with spectral analysis, A. Schwartz and his team for their technical assistance, and J. Harris, W. Risk and H. Coufal for their support. L.V. acknowledges a Yansouni Family Stanford graduate fellowship. This work was supported in part by the QuARC project under a DARPA Quantum Information Science and Technology grant.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Vandersypen, L., Steffen, M., Breyta, G. et al. Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887 (2001). https://doi.org/10.1038/414883a
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/414883a
This article is cited by
-
Effective prime factorization via quantum annealing by modular locally-structured embedding
Scientific Reports (2024)
-
Quantum clock synchronization under decoherence effect
Applied Physics B (2024)
-
On the Various Ways of Quantum Implementation of the Modular Exponentiation Function for Shor’s Factorization
International Journal of Theoretical Physics (2024)
-
Concrete quantum cryptanalysis of binary elliptic curves via addition chain
Quantum Information Processing (2024)
-
Scalable and robust quantum computing on qubit arrays with fixed coupling
npj Quantum Information (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.