Abstract
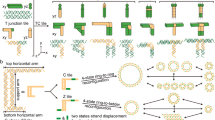
Recent work1,2,3 has demonstrated the self-assembly of designed periodic two-dimensional arrays composed of DNA tiles, in which the intermolecular contacts are directed by ‘sticky’ ends. In a mathematical context, aperiodic mosaics may be formed by the self-assembly of ‘Wang’ tiles4, a process that emulates the operation of a Turing machine. Macroscopic self-assembly has been used to perform computations5; there is also a logical equivalence between DNA sticky ends and Wang tile edges6,7. This suggests that the self-assembly of DNA-based tiles could be used to perform DNA-based computation8. Algorithmic aperiodic self-assembly requires greater fidelity than periodic self-assembly, because correct tiles must compete with partially correct tiles. Here we report a one-dimensional algorithmic self-assembly of DNA triple-crossover molecules9 that can be used to execute four steps of a logical (cumulative XOR) operation on a string of binary bits.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Winfree, E., Liu, F., Wenzler, L. A. & Seeman, N. C. Design and self-assembly of two-dimensional DNA crystals. Nature 394, 539–544 (1998).
Liu, F., Sha, R. & Seeman, N. C. Modifying the surface features of two-dimensional DNA crystals. J. Am. Chem. Soc. 121, 917– 922 (1999).
Mao, C., Sun, W. & Seeman N. C. Designed two-dimensional DNA Holliday junction arrays visualized by atomic force microscopy. J. Am. Chem. Soc. 121, 5437–5443 (1999).
Wang, H. in Proceedings of a Symposium in the Mathematical Theory of Automata 23–26 (Polytechnic Press, New York, 1963).
Rothemund, P. W. K. Using lateral capillary forces to compute by self-assembly. Proc. Nat. Acad. Sci. USA 97, 984– 989 (2000).
Winfree, E. in DNA Based Computers: Proceedings of a DIMACS Workshop, April 4, 1995, Princeton University (eds Lipton, R. J. & Baum, E. B.) 199– 221 (American Mathematical Society, Providence, RI, 1996).
Winfree, E. Algorithmic Self-Assembly of DNA. PhD Thesis, Caltech ( 1998).
Adleman, L. Molecular computation of solutions to combinatorial problems. Science 266, 1021–1024 ( 1994).
LaBean, T. et al. The construction, analysis, ligation and self-assembly of DNA triple crossover complexes. J. Am. Chem. Soc. 122, 1848–1860 (2000).
Seeman, N. C. Nucleic acid nanostructures and topology. Angew. Chem. Int. Edn Engl. 37, 3220–3238 ( 1998).
Faulhammer, D., Cukras, A. R., Lipton, R. J. & Landweber, L. F. Molecular computation: RNA solutions to chess problems. Proc. Natl Acad. Sci. USA 97, 1385–1389 (2000).
Harada, K. & Orgel, L. E. Unexpected substrate specificity of T4 DNA ligase revealed by in vitro selection. Nucleic Acids Res. 21, 2287–2291 (1993).
Winfree, E., Yang, X. & Seeman, N. C. in DNA Based Computers: II Proceedings of a DIMACS Workshop, June 10–12, 1996, Princeton University (eds Landweber, L. F. & Baum, E. B.) 217–254 (American Mathematical Society, Providence, RI, 1999).
Liu, Q. et al. DNA computing on surfaces. Nature 403, 175–179 (2000).
Pirrung, M. C. et al. The arrayed primer extension method for DNA microchip analysis. Molecular computation of satisfaction problems. J. Am. Chem. Soc. 122, 1873–1882 ( 2000).
Sakamoto, K. et al. Molecular computation by DNA hairpin formation. Science 288, 1223–1226 ( 2000).
Gehani, A., LaBean, T. H. & Reif, J. H. in DNA Based Computers: Proceedings of a DIMACS Workshop, June 1999, MIT (ed. E. Winfree) (DIMACS Series in Discrete Mathematics and Theoretical Computer Science, American Mathematical Society, Providence, RI, in the press).
Reif, J. H. in DNA Based Computers: III Proceedings of a DIMACS Workshop, June 23–25, 1997, University of Pennsylvania (eds Rubin, H. & Wood D. H.) 217–254 (American Mathematical Society, Providence, RI, 1999).
Acknowledgements
We thank E. Winfree and A. Carbone for valuable discussions. This work has been supported by grants from DARPA and the National Science Foundation to J.H.R. and N.C.S.; ONR, USAF, NSF and NIH grants to N.C.S.; and NSF and ARO grants to J.H.R.
Author information
Authors and Affiliations
Corresponding author
Supplementary information
Rights and permissions
About this article
Cite this article
Mao, C., LaBean, T., Reif, J. et al. Logical computation using algorithmic self-assembly of DNA triple-crossover molecules. Nature 407, 493–496 (2000). https://doi.org/10.1038/35035038
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/35035038
This article is cited by
-
Bounded Wang tilings with integer programming and graph-based heuristics
Scientific Reports (2023)
-
Generic and scalable DNA-based logic design methodology for massive parallel computation
The Journal of Supercomputing (2023)
-
Ned Seeman (1945–2021)
Nature (2021)
-
DNA structures embedded with functionalized nanomaterials for biophysical applications
Journal of the Korean Physical Society (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.