Abstract
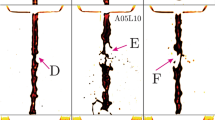
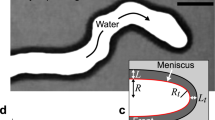
What happens when one attempts to push water through a fluid of higher viscosity? Under appropriate experimental conditions, the water breaks through in the form of highly branched patterns called viscous fingers. Water was used to push a more viscous but miscible, non-newtonian fluid in a Hele-Shaw cell. The resulting viscous finger instability was found to be a fractal growth phenomenon. Reproducible values of the fractal dimension df were found and were interpreted using a modification of the diffusion limited aggregation model.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
Saffman, P. G. & Taylor, G. I. Proc. R. Soc. A245, 312–329 (1958).
Chuoke, R. L., Van Meurs, P. & Van der Poel, C. J. petrol. Tech. 11, 64–70 (1959).
Stalkup, F. I. Miscible Displacements (Soc. of Petroleum Eng., AIME, N.Y., 1983).
Hele Shaw, J. S. S. Nature 58, 34–36 (1898).
Mandelbrot, B. B. The Fractal Geometry of Nature (Freeman, San Francisco, 1982).
Brady, R. M. & Ball, R. C. Nature 309, 225–229 (1984).
Avnir, D., Farin, D. & Pfeiffer, P. Nature 308, 261–263 (1984).
Matsushita, M., Sano, M., Hayakawa, Y., Honjo, H. & Sawada, Y. Phys. Rev. Lett. 53, 286–289 (1984).
Powles, J. G. & Quirke, N. Phys. Rev. Lett. 52, 1571–1574 (1984).
Forrest, S. L. & Witten, T. A. J. Phys. A12, L109–112 (1979).
Lamb, H. Hydrodynamics (Cambridge University Press, London, 1932).
Chandrasekhar, S. Rev. mod. Phys. 15, 1–89 (1943).
Witten, T. A. & Sander, L. M. Phys. Rev. Lett. 47, 1499–1501 (1981).
Witten, T. A. & Sander, L. M. Phys. Rev. B27, 5685–5697 (1983).
Herrmann, H. J. Phys. Rep. (in the press).
Stanley, H. E. Fractals in Statistical Physics (Oxford University Press, New York, 1985).
Meakin, P. Phys. Rev. A27, 1495–1507 (1983).
Peters, E. J. & Flock, D. L. J. Soc. petrol. Engng 21, 249–258 (1981).
Paterson, L. J. Fluid Mech. 113, 513–529 (1981).
Todd, M. R. & Longstaff, W. J. J. petrol. Tech. 253, 874–882 (1972).
Stanley, H. E. Introduction to Phase Transitions and Critical Phenomena (Oxford University Press, 1971).
Niemeyer, L., Pietronero, L. & Wiesmann, H. J. Phys. Rev. Lett. 52, 1033–1036 (1984).
Paterson, L. Phys. Rev. Lett. 52, 1621–1624 (1984).
Maher, J. V. Phys. Rev. Lett. (submitted).
Tang, C. Phys. Rev. A (submitted).
Kadanoff, L. P. J. stat. Phys. (submitted).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Nittmann, J., Daccord, G. & Stanley, H. Fractal growth viscous fingers: quantitative characterization of a fluid instability phenomenon. Nature 314, 141–144 (1985). https://doi.org/10.1038/314141a0
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/314141a0
This article is cited by
-
Air invasion into three-dimensional foam induces viscous fingering instabilities
Scientific Reports (2024)
-
Stability Analysis of Miscible Viscous Fingering in Bingham and Carreau Fluids
Transport in Porous Media (2022)
-
Fractal structures arising from interfacial instabilities in bio-oil atomization
Scientific Reports (2021)
-
Unstable Displacement of Non-aqueous Phase Liquids with Surfactant and Polymer
Transport in Porous Media (2019)
-
On the displacement of two immiscible Oldroyd-B fluids in a Hele-Shaw cell
ANNALI DELL'UNIVERSITA' DI FERRARA (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.