Abstract
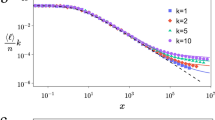
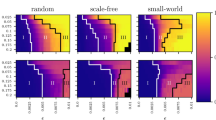
Networks of coupled dynamical systems have been used to model biological oscillators1,2,3,4, Josephson junction arrays5,6, excitable media7, neural networks8,9,10, spatial games11, genetic control networks12 and many other self-organizing systems. Ordinarily, the connection topology is assumed to be either completely regular or completely random. But many biological, technological and social networks lie somewhere between these two extremes. Here we explore simple models of networks that can be tuned through this middle ground: regular networks ‘rewired’ to introduce increasing amounts of disorder. We find that these systems can be highly clustered, like regular lattices, yet have small characteristic path lengths, like random graphs. We call them ‘small-world’ networks, by analogy with the small-world phenomenon13,14 (popularly known as six degrees of separation15). The neural network of the worm Caenorhabditis elegans, the power grid of the western United States, and the collaboration graph of film actors are shown to be small-world networks. Models of dynamical systems with small-world coupling display enhanced signal-propagation speed, computational power, and synchronizability. In particular, infectious diseases spread more easily in small-world networks than in regular lattices.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Winfree, A. T. The Geometry of Biological Time(Springer, New York, 1980).
Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence(Springer, Berlin, 1984).
Strogatz, S. H. & Stewart, I. Coupled oscillators and biological synchronization. Sci. Am. 269(6), 102–109 (1993).
Bressloff, P. C., Coombes, S. & De Souza, B. Dynamics of a ring of pulse-coupled oscillators: a group theoretic approach. Phys. Rev. Lett. 79, 2791–2794 (1997).
Braiman, Y., Lindner, J. F. & Ditto, W. L. Taming spatiotemporal chaos with disorder. Nature 378, 465–467 (1995).
Wiesenfeld, K. New results on frequency-locking dynamics of disordered Josephson arrays. Physica B 222, 315–319 (1996).
Gerhardt, M., Schuster, H. & Tyson, J. J. Acellular automaton model of excitable media including curvature and dispersion. Science 247, 1563–1566 (1990).
Collins, J. J., Chow, C. C. & Imhoff, T. T. Stochastic resonance without tuning. Nature 376, 236–238 (1995).
Hopfield, J. J. & Herz, A. V. M. Rapid local synchronization of action potentials: Toward computation with coupled integrate-and-fire neurons. Proc. Natl Acad. Sci. USA 92, 6655–6662 (1995).
Abbott, L. F. & van Vreeswijk, C. Asynchronous states in neural networks of pulse-coupled oscillators. Phys. Rev. E 48(2), 1483–1490 (1993).
Nowak, M. A. & May, R. M. Evolutionary games and spatial chaos. Nature 359, 826–829 (1992).
Kauffman, S. A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 22, 437–467 (1969).
Milgram, S. The small world problem. Psychol. Today 2, 60–67 (1967).
Kochen, M. (ed.) The Small World(Ablex, Norwood, NJ, 1989).
Guare, J. Six Degrees of Separation: A Play(Vintage Books, New York, 1990).
Bollabás, B. Random Graphs(Academic, London, 1985).
Achacoso, T. B. & Yamamoto, W. S. AY's Neuroanatomy of C. elegans for Computation(CRC Press, Boca Raton, FL, 1992).
Wasserman, S. & Faust, K. Social Network Analysis: Methods and Applications(Cambridge Univ. Press, 1994).
Phadke, A. G. & Thorp, J. S. Computer Relaying for Power Systems(Wiley, New York, 1988).
Sattenspiel, L. & Simon, C. P. The spread and persistence of infectious diseases in structured populations. Math. Biosci. 90, 341–366 (1988).
Longini, I. M. J Amathematical model for predicting the geographic spread of new infectious agents. Math. Biosci. 90, 367–383 (1988).
Hess, G. Disease in metapopulation models: implications for conservation. Ecology 77, 1617–1632 (1996).
Blythe, S. P., Castillo-Chavez, C. & Palmer, J. S. Toward a unified theory of sexual mixing and pair formation. Math. Biosci. 107, 379–405 (1991).
Kretschmar, M. & Morris, M. Measures of concurrency in networks and the spread of infectious disease. Math. Biosci. 133, 165–195 (1996).
Das, R., Mitchell, M. & Crutchfield, J. P. in Parallel Problem Solving from Nature(eds Davido, Y., Schwefel, H.-P. & Männer, R.) 344–353 (Lecture Notes in Computer Science 866, Springer, Berlin, 1994).
Axelrod, R. The Evolution of Cooperation(Basic Books, New York, 1984).
Gray, C. M., König, P., Engel, A. K. & Singer, W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature 338, 334–337 (1989).
Acknowledgements
We thank B. Tjaden for providing the film actor data, and J. Thorp and K. Bae for the Western States Power Grid data. This work was supported by the US National Science Foundation (Division of Mathematical Sciences).
Author information
Authors and Affiliations
Author notes
Correspondence and requests for materials should be addressed to D.J.W.
- Duncan J. Watts
Corresponding author
Rights and permissions
About this article
Cite this article
Watts, D., Strogatz, S. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998). https://doi.org/10.1038/30918
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/30918
This article is cited by
-
ECDEP: identifying essential proteins based on evolutionary community discovery and subcellular localization
BMC Genomics (2024)
-
Modelling the impact of human behavior using a two-layer Watts-Strogatz network for transmission and control of Mpox
BMC Infectious Diseases (2024)
-
Long ties accelerate noisy threshold-based contagions
Nature Human Behaviour (2024)
-
A study of correlations between cephalometric measurements in Koreans with normal occlusion by network analysis
Scientific Reports (2024)
-
Reactivation of encoding ensembles in the prelimbic cortex supports temporal associations
Neuropsychopharmacology (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.