Abstract
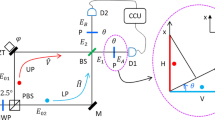
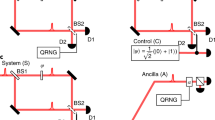
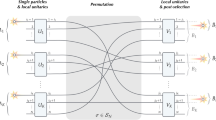
Motivated by the question of which kind of physical interactions and processes are needed for the production of quantum entanglement, Peres has put forward the radical idea of delayed-choice entanglement swapping. There, entanglement can be ‘produced a posteriori, after the entangled particles have been measured and may no longer exist’. Here, we report the realization of Peres’s gedanken experiment. Using four photons, we can actively delay the choice of measurement—implemented through a high-speed tunable bipartite-state analyser and a quantum random-number generator—on two of the photons into the time-like future of the registration of the other two photons. This effectively projects the two already registered photons onto one of two mutually exclusive quantum states in which the photons are either entangled (quantum correlations) or separable (classical correlations). This can also be viewed as ‘quantum steering into the past’.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Change history
26 April 2012
In the version of this Article originally published online, the definition of the witness operator given in the paragraph after equation (4) was incorrect. This error has been corrected in all versions of the Article.
References
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Schrödinger, E. Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften 23, 807–812; 823–828; 844–849 (1935). English translation in Proc. Am. Philos. Soc. 124, (1980), reprinted in Wheeler, J. A. & Zurek, W. H. (eds) Quantum Theory and Measurement 152–167 (Princeton Univ. Press,1984).
Žukowski, M., Zeilinger, A., Horne, M. A. & Ekert, A. K. ‘Event-ready-detectors’ Bell experiment via entanglement swapping. Phys. Rev. Lett. 71, 4287–4290 (1993).
Peres, A. Delayed choice for entanglement swapping. J. Mod. Opt. 47, 139–143 (2000).
Cohen, O. Counterfactual entanglement and nonlocal correlations in separable states. Phys. Rev. A 60, 80–84 (1999).
Jennewein, T., Achleitner, U., Weihs, G., Weinfurter, H. & Zeilinger, A. A fast and compact quantum random number generator. Rev. Sci. Instrum. 71, 1675–1680 (2000).
Bohr, N. in Quantum Theory and Measurement (eds Wheeler, J. A. & Zurek, W. H.) 9–49 (Princeton Univ. Press, 1984).
Wheeler, J. A. Mathematical Foundations of Quantum Theory 9–48 (Academic, 1978).
Wheeler, J. A. in Quantum Theory and Measurement (eds Wheeler, J. A. & Zurek, W. H.) 182–213 (Princeton Univ. Press, 1984).
Alley, C. O., Jacubowicz, O. G. & Wickes, W. C. in Proc. Second International Symposium on the Foundations of Quantum Mechanics (ed. Narani, H.) 36–47 (Physics Society of Japan, 1987).
Hellmut, T., Walther, H., Zajonc, A. G. & Schleich, W. Delayed-choice experiments in quantum interference. Phys. Rev. A 35, 2532–2541 (1987).
Baldzuhn, J., Mohler, E. & Martienssen, W. A wave-particle delayed-choice experiment with a single-photon state. Z. Phys. B 77, 347–352 (1989).
Kim, Y-H., Yu, R., Kulik, S., Shih, Y. & Scully, M. O. Delayed ‘choice’ quantum eraser. Phys. Rev. Lett. 84, 1–4 (2000).
Jacques, V. et al. Experimental realization of Wheeler’s delayed-choice gedanken experiment. Science 315, 966–968 (2007).
Jacques, V. et al. Delayed-choice test of quantum complementarity with interfering single photons. Phys. Rev. Lett. 100, 220402 (2008).
Jennewein, T., Weihs, G., Pan, J-W. & Zeilinger, A. Experimental nonlocality proof of quantum teleportation and entanglement swapping. Phys. Rev. Lett. 88, 017903 (2001).
Sciarrino, F., Lombardi, E., Milani, G. & De Martini, F. Delayed-choice entanglement swapping with vacuum–one-photon quantum states. Phys. Rev. A 66, 024309 (2002).
Schrödinger, E. Discussion of probability relations between separated systems. Proc. Camb. Phil. Soc. 31, 555–563 (1935).
Aspect, A., Dalibard, J. & Roger, G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 49, 1804–1807 (1982).
Weihs, G. et al. Violation of Bell’s inequality under strict Einstein locality conditions. Phys. Rev. Lett. 81, 5039–5043 (1998).
Scheidl, T. et al. Violation of local realism with freedom of choice. Proc. Natl Acad. Sci. USA 107, 19708–19713 (2010).
Coffman, V., Kundu, J. & Wootters, W. K. Distributed entanglement. Phys. Rev. A 61, 052306 (1993).
Pan, J-W., Bouwmeester, D., Weinfurter, H. & Zeilinger, A. Experimental entanglement swapping: Entangling photons that never interacted. Phys. Rev. Lett. 80, 3891–3894 (1998).
Riebe, M. et al. Deterministic quantum teleportation with atoms. Nature 429, 734–737 (2004).
Barrett, M. D. et al. Deterministic quantum teleportation of atomic qubits. Nature 429, 737 (2004).
Matsukevich, D. N., Maunz, P., Moehring, D. L., Olmschenk, S. & Monroe, C. Bell inequality violation with two remote atomic qubits. Phys. Rev. Lett. 100, 150404 (2008).
Halder, M. et al. Entangling independent photons by time measurement. Nature Phys. 3, 692–695 (2007).
Yuan, Z-S. et al. Experimental demonstration of a BDCZ quantum repeater node. Nature 454, 1098–1101 (2008).
Kaltenbaek, R., Prevedel, R., Aspelmeyer, M. & Zeilinger, A. High-fidelity entanglement swapping with fully independent sources. Phys. Rev. A. 79, 040302 (2009).
Briegel, H-J., Duer, W., Cirac, J. I. & Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Duan, L-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Chen, Y-A. et al. Experimental quantum secret sharing and third-man quantum cryptography. Phys. Rev. Lett. 95, 200502 (2005).
Simon, C. & Irvine, W. T. M. Robust long-distance entanglement and a loophole-free Bell test with ions and photons. Phys. Rev. Lett. 91, 110405 (2003).
Greenberger, D. M., Horne, M. & Zeilinger, A. Bell theorem without inequalities for two particles. I. Efficient detectors. Phys. Rev. A. 78, 022110 (2008).
Greenberger, D. M., Horne, M., Zeilinger, A. & Žukowski, M. Bell theorem without inequalities for two particles. II. Inefficient detectors. Phys. Rev. A. 78, 022111 (2008).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Mattle, K., Weinfurter, H., Kwiat, P. G. & Zeilinger, A. Dense coding in experimental quantum communication. Phys. Rev. Lett. 76, 4656–4659 (1996).
Jennewein, T., Aspelmeyer, M., Brukner, Č. & Zeilinger, A. Experimental proposal of switched delayed-choice for entanglement swapping. Int. J. Quant. Info. 3, 73–79 (2005).
Kwiat, P. G. et al. New high-intensity source of polarization-entangled photon pairs. Phys. Rev. Lett. 75, 4337–4341 (1995).
Brukner, Č., Aspelmeyer, M. & Zeilinger, A. Complementarity and information in delayed-choice for entanglement swapping. Found. Phys. 35, 1909–1919 (2005).
Ma, X-S. et al. A high-speed tunable beam splitter for feed-forward photonic quantum information processing. Opt. Express 19, 22723–22730 (2011).
Gühne, O. et al. Detection of entanglement with few local measurements. Phys. Rev. A 66, 062305 (2002).
Zhang, Q. et al. Experimental quantum teleportation of a two-qubit composite system. Nature Phys. 2, 678–682 (2006).
Gühne, O. & Toth, G. Entanglement detection. Phys. Rep. 474, 1–75 (2009).
Žukowski, M., Zeilinger, A. & Weinfurter, H. Entangling photons radiated by independent pulsed sources. Ann. N.Y. Acad. Sci. 755, 91–102 (1995).
Acknowledgements
We are grateful to N. Tetik and A. Qarry for help during the early stages of the experiment, and M. Aspelmeyer and P. Walther for fruitful discussions. We acknowledge support from the European Commission, Q-ESSENCE (No. 248095), ERC Advanced Senior Grant (QIT4QAD) and the John Templeton Foundation, as well as SFB-FOQUS and the Doctoral Program CoQuS of the Austrian Science Fund (FWF).
Author information
Authors and Affiliations
Contributions
X-s.M. designed and carried out the experiment and analysed data. S.Z. provided experimental assistance. J.K. provided the theoretical analysis and analysed data. R.U. provided experimental and conceptual assistance. T.J. conceived the research, planned and performed the experiment and analysed data. Č.B. provided theoretical suggestions and analysis. A.Z. conceived the research, designed the experiment and supervised the project. All authors wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 599 kb)
Rights and permissions
About this article
Cite this article
Ma, Xs., Zotter, S., Kofler, J. et al. Experimental delayed-choice entanglement swapping. Nature Phys 8, 479–484 (2012). https://doi.org/10.1038/nphys2294
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2294
This article is cited by
-
Delayed choice experiments: an analysis in forward time
Quantum Studies: Mathematics and Foundations (2024)
-
Quantum causality emerging in a delayed-choice quantum Cheshire Cat experiment with neutrons
Scientific Reports (2023)
-
Indefinite causal order with fixed temporal order for electrons and positrons
Quantum Studies: Mathematics and Foundations (2023)
-
Entanglement and the Path Integral
Foundations of Physics (2023)
-
Experimental assessment of physical realism in a quantum-controlled device
Communications Physics (2022)