Abstract
Our ability to control friction remains modest, as our understanding of the underlying microscopic processes is incomplete1,2,3. Atomic force experiments4,5,6,7,8,9,10,11,12,13,14 have provided a wealth of results on the dependence of nanofriction on structure5,6, velocity7,8,9,10 and temperature11,12,13, but limitations in the dynamic range, time resolution, and control at the single-atom level have hampered a description from first principles3. Here, using an ion-crystal system with single-atom, single-substrate-site spatial and single-slip temporal resolution15,16, we measure the friction force over nearly five orders of magnitude in velocity, and contiguously observe four distinct regimes, while controlling temperature and dissipation. We elucidate the interplay between thermal and structural lubricity for two coupled atoms, and provide a simple explanation in terms of the Peierls–Nabarro potential17. This extensive control at the atomic scale enables fundamental studies of the interaction of many-atom surfaces, possibly into the quantum regime.
Similar content being viewed by others
Main
In the simplest scenario for stick–slip friction, a single atom at an object–substrate interface experiences a force resisting its motion due to a periodic potential created by the substrate2 (Fig. 1a). A finite external force is then required to cause the atom to slip from one potential well to the next across an energy barrier UB. Interestingly, in the case of more than one atom forming the contact interface, friction can be greatly reduced by a structural mismatch of the object and substrate, an effect coined superlubricity5,6,15,18, and observed in friction force microscopy5,6, colloidal monolayers19, and recently in our friction simulator15. Thermally activated transitions between neighbouring potential wells at temperatures T ∼ UB can also reduce the friction force significantly, making it velocity-dependent7,8,9,10,13,20,21,22,23,24. Separate observations have spanned from the high-temperature regime of thermolubricity21 to the low-temperature regime of strong stick–slip8. In the present work, as a function of velocity, we observe the continuous transition between four regimes: thermal drift21, where friction is small and (nearly) velocity-independent; thermal activation7,8,10,21,24, where friction increases logarithmically with velocity; the friction plateau8,9, where friction is large and nearly velocity-independent; and velocity weakening20, where friction decreases with velocity because the damping is not fast enough to remove the energy released in a slip. For a two-atom contact, we observe that the measured friction force is substantially reduced by the interaction between the atoms when they are arranged so as to cancel the forces from the substrate. In our previous work15, we had observed this effect for multiple atoms as a continuous transition from stick–slip to superlubricity when varying the arrangement of the atoms, while driving at a fixed large velocity where thermal effects are minor. In the present work, we link this structural lubricity to a reduced barrier  in the Peierls–Nabarro potential17,25,26, and distinguish structurally induced thermolubricity (
in the Peierls–Nabarro potential17,25,26, and distinguish structurally induced thermolubricity ( ) from structural lubricity (
) from structural lubricity ( ) by observing the full velocity dependence.
) by observing the full velocity dependence.
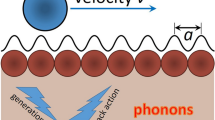
a,b, Model of the friction interface; one Yb+ ion of mass m = 2.9 × 10−25 kg (or two coupled ions separated by a distance d ≍ 5 μm) is confined in a Paul trap27 with a spring constant K = mω02 (ω0/2π = 363 kHz), whose equilibrium point is translated at a constant velocity v by applying a time-varying electric field. An optical standing wave, detuned by ∼12 GHz from the atomic 2S1/2 → 2P1/2 transition, creates a sinusoidal potential of periodicity a = 185 nm and depth Ul/h ≍ 20 MHz along the radiofrequency nodal line of the Paul trap16. The ion is kept at a temperature T ≍ 40 μK by means of continuous laser cooling with a dissipation rate constant γ = τc−1 ≍ 104 s−1. c,d, Temperature dependence of stick–slip friction. At low temperature or high velocity, the ion (red solid circle) sticks in its initial well, corresponding to a rise in its scattered fluorescence (1–2, dark blue open circles) until it slips to the next well, and the added energy is dissipated through laser cooling (3, dark blue open circles). The ion fluorescence is highest when the slip occurs. At high temperature or low velocity, the ion thermalizes over the energy barrier (1–2), and so smoothly transitions to the next well without frictional dissipation (3). If the trap translation direction is reversed, maximum hysteresis is observed in the low-temperature or high-velocity regime (dark open symbols). A reduced hysteresis is present for an intermediate temperature or velocity regime (light filled symbols). The friction force F is measured by means of the separation 2F between the slips in the hysteresis loop. Error bars are statistical and represent one standard deviation.
Our implementation15,16,27 of a friction interface, which simulates solid-state nanofriction26,28,29 with an atomically sharp tip4, consists of one or two electrically trapped atomic ions pulled against the sinusoidal potential (Fig. 1a, b) of a standing wave of light (optical lattice)16,30,31. We observe each ion’s trajectory with resolution finer than the lattice period by means of the ion’s position-dependent fluorescence15. Each time the ion slips into the next well, its fluorescence reaches a maximum and decreases as the ion is laser-cooled into the new potential minimum (Fig. 1c, d). Hysteresis in the timing of the slip as the electrostatic parabolic trapping potential is pulled back and forth reveals the maximum static friction force exerted by the lattice on the ion (Fig. 1d). At finite ion temperature T, the observed hysteresis and corresponding friction force are reduced (Fig. 1c, d).
At zero temperature2,3,22, the dynamical behaviour is determined by the ratio of the lattice confinement frequency  to the electrostatic confinement frequency
to the electrostatic confinement frequency  , where Ul is the depth of the lattice potential, and K is the spring constant of the electrostatic trap (Fig. 1a). The corresponding dimensionless corrugation parameter η = ωl2/ω02 determines the number of minima in the overall potential energy landscape. For η ≤ 1, there is no stick–slip friction as only a single minimum is translated with the applied force. In our regime of interest, 1 < η < 4.6, there are at most two local minima in the overall potential at any time, separated by a maximum energy barrier UB/Ul ≃ (η − 1)2/η2. At finite temperature, the ion can also slip owing to thermal activation before the barrier height is reduced to zero by the applied force (Fig. 1c), leading to a reduced hysteresis and friction (thermolubricity) that depend on the transport velocity v.
, where Ul is the depth of the lattice potential, and K is the spring constant of the electrostatic trap (Fig. 1a). The corresponding dimensionless corrugation parameter η = ωl2/ω02 determines the number of minima in the overall potential energy landscape. For η ≤ 1, there is no stick–slip friction as only a single minimum is translated with the applied force. In our regime of interest, 1 < η < 4.6, there are at most two local minima in the overall potential at any time, separated by a maximum energy barrier UB/Ul ≃ (η − 1)2/η2. At finite temperature, the ion can also slip owing to thermal activation before the barrier height is reduced to zero by the applied force (Fig. 1c), leading to a reduced hysteresis and friction (thermolubricity) that depend on the transport velocity v.
We observe, for the first time in a single experiment, four contiguous regimes of friction with distinct velocity dependences (Fig. 2a). These regimes can be organized by the hierarchy of three timescales, namely the thermal hopping time between lattice wells τth, the transport time for the external trap to move by one lattice well a/v, and the ion recooling time τc. When τth ≪ a/v, thermal hopping dominates, and the ion remains in thermal equilibrium, following the slowly moving ion trap—a regime called thermal drift, where the friction force due to stick–slip (almost) vanishes21. In the thermal activation regime τth ∼ a/v, the stick–slip process is only partially suppressed by thermal fluctuations and contributes to an average friction force, which grows logarithmically with velocity7. For even larger velocities τth ≫ a/v ≫ τc, thermal hopping across lattice wells is negligible on the transport timescale a/v. This is the friction plateau regime, where the friction force reaches its maximum value8. We also observe a fourth regime of friction, sometimes called velocity weakening20, where the friction force decreases logarithmically with velocity13. In our system, this regime arises because the ion does not have sufficient time to recool after the slip for a/v ≲ τc. This effectively increases the ion’s kinetic energy before the next slip event and reduces the friction force (Fig. 2a). Having direct access to all system parameters through independent microscopic measurements, we also show a full-dynamics simulation22,23, without any free parameters, that closely follows our data over all four regimes of friction. Figure 2a furthermore shows that, in the thermal activation and velocity weakening regimes, simple analytical models for the velocity-dependent friction developed previously3,23,24 match our data quantitatively (Supplementary Information). The same good agreement between experimental data and theoretical models is attained when we change the barrier depth UB or the temperature T (Fig. 2b).
The transport time a/v should be compared to two timescales: the thermal hopping time between two lattice wells, given by τth = τ0exp(UB/kBT) for a maximum barrier height UB (where kB is the Boltzmann constant and τ0(τc, ω0, ωl) is the hopping attempt time23,24); and the recooling time after a slip τc. a, Here τth ≍ 10 ms and τc ≍ 100 μs. Four regimes of friction are observed. The friction force is normalized by its zero-temperature maximum value for η = 2.2, Fη=2.2 ≍ 0.36 πUl/a. Here Ul/h = 9.5 MHz and kBT/Ul = 0.15(4). The solid orange line shows the expected result  , where vth ∼ 1 mm s−1, from an analytical model in the thermal activation regime3,23,24. Similarly in the velocity weakening regime, we model the friction as
, where vth ∼ 1 mm s−1, from an analytical model in the thermal activation regime3,23,24. Similarly in the velocity weakening regime, we model the friction as  (orange dotted line), where kBT/Ul = 0.3 and vc = a/τc ∼ 2 mm s−1 (Supplementary Information). The Langevin simulation (dashed green line) is in good agreement with the data over all four velocity regimes for parameters η = 2.2, kBT/Ul = 0.15, τc = 100 μs. b, At a larger lattice depth Ul/h = 20 MHz, where η = 4.6, increasing the temperature from kBT/Ul = 0.04(1) (blue squares) to kBT/Ul = 0.17(1) (red diamonds) reduces the friction in the thermal activation region 10−5 m s−1 ≲ v ≲ 10−3 m s−1 while leaving the friction plateau in the region 10−3 m s−1 ≲ v ≲ 10−2 m s−1 almost unaffected. Here, τc ≍ 50 μs. The friction force is normalized by its zero-temperature maximum value for η = 4.6, Fη=4.6 ≍ 0.61πUl/a. Solid lines show the expected results from the analytical thermal activation model. Data from a, normalized to Fη=4.6 is shown as open black circles. Langevin simulations (inset, solid lines) are in good agreement with the data for parameters η = 4.6, kBT/Ul = 0.05 (blue), kBT/Ul = 0.13 (red), τc = 50 μs. Error bars are statistical and represent one standard deviation.
(orange dotted line), where kBT/Ul = 0.3 and vc = a/τc ∼ 2 mm s−1 (Supplementary Information). The Langevin simulation (dashed green line) is in good agreement with the data over all four velocity regimes for parameters η = 2.2, kBT/Ul = 0.15, τc = 100 μs. b, At a larger lattice depth Ul/h = 20 MHz, where η = 4.6, increasing the temperature from kBT/Ul = 0.04(1) (blue squares) to kBT/Ul = 0.17(1) (red diamonds) reduces the friction in the thermal activation region 10−5 m s−1 ≲ v ≲ 10−3 m s−1 while leaving the friction plateau in the region 10−3 m s−1 ≲ v ≲ 10−2 m s−1 almost unaffected. Here, τc ≍ 50 μs. The friction force is normalized by its zero-temperature maximum value for η = 4.6, Fη=4.6 ≍ 0.61πUl/a. Solid lines show the expected results from the analytical thermal activation model. Data from a, normalized to Fη=4.6 is shown as open black circles. Langevin simulations (inset, solid lines) are in good agreement with the data for parameters η = 4.6, kBT/Ul = 0.05 (blue), kBT/Ul = 0.13 (red), τc = 50 μs. Error bars are statistical and represent one standard deviation.
The friction force is expected to be particularly sensitive to temperature when τth ≲ a/v, owing to exponential activation21, and almost independent of it when τth ≫ a/v. In Fig. 3, we verify experimentally11,12,13 that for low velocities (τth ≤ a/v) the friction force changes by an order of magnitude when we change the temperature by a factor of seven (Supplementary Information), whereas for high velocities (τth ≫ a/v) the force varies by less than a factor of two. This confirms that an effectively zero-temperature stick–slip regime15 can be experimentally accessed at high transport velocity v ≫ a/τth.
In the thermal drift regime τth ≪ a/v, the friction force is proportional to exp(Ul/kBT), whereas it depends only weakly on temperature in the friction plateau regime23 τth ≫ a/v. We vary temperature from kBT/Ul = 0.06 to kBT/Ul = 0.4, and show the friction force on a logarithmic scale against 1/T. We fit data to the model F/Fη=4.6 = fexp(cUl/kBT), where f is a free parameter, and c represents the fitted sensitivity to temperature and is close to unity in the thermal drift regime. For a high velocity (v ≍ 1 mm s−1) corresponding to the friction plateau regime (green), friction is almost constant for Ul/kBT ≥ 5, and the fit to the model in this temperature range (dashed green line) gives c = 0.016—that is, a very weak temperature dependence. For a low velocity (v ≍ 40 μm s−1) close to the regime of thermal drift (orange), the friction force is sensitive to temperature, and the fit to the model (red dashed line) gives c = 0.17. Experimental parameters are η = 4.6, Ul/h = 20 MHz and τc ≍ 50 μs. Error bars are statistical and represent one standard deviation.
To study the interplay between structural lubricity, arising from mismatch between the object and substrate corrugations, and thermolubricity, we place a second ion in the trap along the optical lattice direction (Fig. 1a, b). If the effective spring force arising from the Coulomb interaction between the ions were infinitely stiff, the friction force on the two-ion system could be made to vanish by placing the two ions at positions where they experience opposite lattice forces. It is the essence of structural lubricity that a substantial friction reduction persists even for finite ion–ion interaction that is comparable to the substrate corrugation. When the ions experience opposite lattice forces, it is energetically favourable for them to pass the energy barrier between wells one at a time, as illustrated by the two-dimensional energy landscapes of Fig. 4d, e. This results in a reduced barrier depth  , and therefore a reduced friction force. Using the electrical trap, the spacing d between the ions can be tuned to be an exact multiple of a (that is, d mod a = 0), or to be mismatched (that is, d mod a = a/2). We have found in our previous work that mismatch greatly reduces the friction force15, as has been also observed for graphite flakes on a graphite substrate under certain orientations5. The friction reduction can be due to pure structural lubricity (stick–slip motion in a Peierls–Nabarro potential17 with reduced energy barrier
, and therefore a reduced friction force. Using the electrical trap, the spacing d between the ions can be tuned to be an exact multiple of a (that is, d mod a = 0), or to be mismatched (that is, d mod a = a/2). We have found in our previous work that mismatch greatly reduces the friction force15, as has been also observed for graphite flakes on a graphite substrate under certain orientations5. The friction reduction can be due to pure structural lubricity (stick–slip motion in a Peierls–Nabarro potential17 with reduced energy barrier  ) or to structurally induced thermolubricity (
) or to structurally induced thermolubricity ( ), easily distinguished experimentally, as only the latter is velocity-dependent.
), easily distinguished experimentally, as only the latter is velocity-dependent.
a–c, Velocity dependence of the friction force for two ions, for η = 4.6. a, In the matched case (red circles), where the ion spacing is an integer multiple of the lattice period a, for kBT/Ul = 0.055(10) the data agree with one ion at approximately the same temperature (blue squares), and reach a maximal value near Fη=4.6. Langevin simulations (solid lines) are in good agreement with data for η = 4.6, kBT/Ul = 0.05. b, In the matched case (red diamonds) for a temperature of kBT/Ul = 0.15(2), the maximal friction is ∼0.7Fη=4.6. By comparison, the friction for the mismatched case (green circles), where the two ions at their unperturbed position experience opposite forces by the optical lattice, at the same temperature of kBT/Ul = 0.15(3), reaches a maximum of ∼0.15Fη=4.6. Finite-temperature Langevin simulations (solid lines) are in good agreement with data for η = 4.6, kBT/Ul = 0.15. c, The ratio of friction forces in the matched and mismatched cases (black circles, 3-point running average) is unity in the low-velocity thermal drift regime, and constant in the high-velocity friction plateau regime, where its value ∼4.8 is mostly due to structural lubricity, in good agreement with Langevin simulations (solid gold line). Although barely visible in the data, the peak in the simulations is due to structurally induced thermolubricity: a window of velocities for which the structural friction reduction is enhanced by thermal activation over a reduced energy barrier  . d,e, Energy potential landscape for two interacting atoms. In the mismatched case (e), the energy barrier
. d,e, Energy potential landscape for two interacting atoms. In the mismatched case (e), the energy barrier  between the wells is reduced by a factor of ∼3.7 and the ions pass the barrier one at a time (inset), compared to the matched case UB (d) where the ions pass the barrier simultaneously (inset). At fixed T for a single ion in the friction plateau regime, this barrier reduction
between the wells is reduced by a factor of ∼3.7 and the ions pass the barrier one at a time (inset), compared to the matched case UB (d) where the ions pass the barrier simultaneously (inset). At fixed T for a single ion in the friction plateau regime, this barrier reduction  would lead to a thermal friction reduction of ∼1.4, as can be inferred from the green data in Fig. 3. The expected total reduction of 3.7 × 1.4 = 5.2 is in good agreement with the observed reduction of ∼4.8. Error bars are statistical and represent one standard deviation.
would lead to a thermal friction reduction of ∼1.4, as can be inferred from the green data in Fig. 3. The expected total reduction of 3.7 × 1.4 = 5.2 is in good agreement with the observed reduction of ∼4.8. Error bars are statistical and represent one standard deviation.
In the matched case, the two-ion system is expected to behave as a rigid object akin to a single particle, because only the centre-of-mass mode is affected by lattice forces. Figure 4a shows that the observed velocity dependence of friction in the matched case indeed agrees with the one-ion case. In the mismatched case, the lattice forces on the centre-of-mass mode cancel out, and we observe that, for the same temperature, friction is significantly reduced compared to the matched case (Fig. 4b), in good agreement with Langevin simulations. When comparing the friction in the mismatched case to the matched case, we find that there is no reduction in the thermal drift regime, and reduction by a factor of ∼4.8 in the friction plateau regime (Fig. 4c). A calculation of the two-ion energy landscape (Fig. 4d, e) shows that in the matched case the barrier is identical to the one-ion case, whereas in the mismatched case it is approximately four times lower ( ). The additional ∼20% friction reduction compared to
). The additional ∼20% friction reduction compared to  can be explained by structurally induced thermolubricity at fixed temperature due to the lower barrier depth
can be explained by structurally induced thermolubricity at fixed temperature due to the lower barrier depth  (Fig. 3). The high-velocity friction reduction plateau of Fig. 4c, where thermal hopping is negligible, then represents a direct observation of structurally induced lubricity or ‘superlubricity’5,6,15,18. This interpretation is consistent with the observation that, in this regime, the ions pass the barrier one at a time (Fig. 4e inset), reminiscent of a kink defect being transported across the two-atom chain17. Thus, measuring the reduced friction force directly reveals the Peierls–Nabarro barrier17
(Fig. 3). The high-velocity friction reduction plateau of Fig. 4c, where thermal hopping is negligible, then represents a direct observation of structurally induced lubricity or ‘superlubricity’5,6,15,18. This interpretation is consistent with the observation that, in this regime, the ions pass the barrier one at a time (Fig. 4e inset), reminiscent of a kink defect being transported across the two-atom chain17. Thus, measuring the reduced friction force directly reveals the Peierls–Nabarro barrier17  for two atoms in a periodic potential.
for two atoms in a periodic potential.
To facilitate comparison of our ion-crystal system with typical solid-state systems, Table 1 summarizes the important physical parameters at play. Although parameters such as the lattice spacing a, the lattice depth Ul, the spring constant K, and the temperature T differ by several orders of magnitude, the important dimensionless parameters2,3,21 that govern the frictional behaviour take on the same range of values in the two systems. In the future, the ion-crystal system could be used to study the more complex behaviours found in the multi-slip friction regime14, and many-body phenomena arising from the strong particle interactions in the corrugated potential, such as the Aubry transition2,17,26,29. Furthermore, cooling to the vibrational ground state may provide access to a regime of quantum friction dominated by quantum tunnelling.
References
Urbakh, M., Klafter, J., Gourdon, D. & Israelachvili, J. The nonlinear nature of friction. Nature 430, 525–528 (2004).
Vanossi, A., Manini, N., Urbakh, M., Zapperi, S. & Tosatti, E. Colloquium: Modeling friction: From nanoscale to mesoscale. Rev. Mod. Phys. 85, 529–552 (2013).
Krylov, S. Y. & Frenken, J. W. M. The physics of atomic-scale friction: Basic considerations and open questions. Phys. Status Solidi 251, 711–736 (2014).
Mate, C., McClelland, G., Erlandsson, R. & Chiang, S. Atomic-scale friction of a tungsten tip on a graphite surface. Phys. Rev. Lett. 59, 1942–1945 (1987).
Dienwiebel, M. et al. Superlubricity of graphite. Phys. Rev. Lett. 92, 126101 (2004).
Socoliuc, A., Bennewitz, R., Gnecco, E. & Meyer, E. Transition from stick–slip to continuous sliding in atomic friction: Entering a new regime of ultralow friction. Phys. Rev. Lett. 92, 134301 (2004).
Gnecco, E. et al. Velocity dependence of atomic friction. Phys. Rev. Lett. 84, 1172–1175 (2000).
Riedo, E., Gnecco, E., Bennewitz, R., Meyer, E. & Brune, H. Interaction potential and hopping dynamics governing sliding friction. Phys. Rev. Lett. 91, 084502 (2003).
Liu, X.-Z. et al. Dynamics of atomic stick–slip friction examined with atomic force microscopy and atomistic simulations at overlapping speeds. Phys. Rev. Lett. 114, 146102 (2015).
Li, Q., Dong, Y., Perez, D., Martini, A. & Carpick, R. W. Speed dependence of atomic stick–slip friction in optimally matched experiments and molecular dynamics simulations. Phys. Rev. Lett. 106, 126101 (2011).
Zhao, X., Phillpot, S., Sawyer, W., Sinnott, S. & Perry, S. Transition from thermal to athermal friction under cryogenic conditions. Phys. Rev. Lett. 102, 186102 (2009).
Jansen, L., Hölscher, H., Fuchs, H. & Schirmeisen, A. Temperature dependence of atomic-scale stick–slip friction. Phys. Rev. Lett. 104, 256101 (2010).
Barel, I., Urbakh, M., Jansen, L. & Schirmeisen, A. Unexpected temperature and velocity dependencies of atomic-scale stick–slip friction. Phys. Rev. B 84, 115417 (2011).
Medyanik, S., Liu, W., Sung, I.-H. & Carpick, R. Predictions and observations of multiple slip modes in atomic-scale friction. Phys. Rev. Lett. 97, 136106 (2006).
Bylinskii, A., Gangloff, D. & Vuletic, V. Tuning friction atom-by-atom in an ion-crystal simulator. Science 348, 1115–1118 (2015).
Karpa, L., Bylinskii, A., Gangloff, D., Cetina, M. & Vuletić, V. Suppression of ion transport due to long-lived subwavelength localization by an optical lattice. Phys. Rev. Lett. 111, 163002 (2013).
Braun, O. M. & Kivshar, Y. S. The Frenkel–Kontorova Model: Concepts, Methods, and Applications (Springer, 2004).
Meyer, E. & Gnecco, E. Superlubricity on the nanometer scale. Friction 2, 106–113 (2014).
Bohlein, T., Mikhael, J. & Bechinger, C. Observation of kinks and antikinks in colloidal monolayers driven across ordered surfaces. Nature Mater. 11, 126–130 (2012).
Jagla, E. A. Velocity weakening and possibility of aftershocks in nanoscale friction experiments. Phys. Rev. B 86, 155408 (2012).
Jinesh, K., Krylov, S., Valk, H., Dienwiebel, M. & Frenken, J. Thermolubricity in atomic-scale friction. Phys. Rev. B 78, 155440 (2008).
Müser, M. Velocity dependence of kinetic friction in the Prandtl–Tomlinson model. Phys. Rev. B 16, 1–15 (2011).
Dong, Y., Vadakkepatt, A. & Martini, A. Analytical models for atomic friction. Tribol. Lett. 44, 367–386 (2011).
Sang, Y., Dubé, M. & Grant, M. Thermal effects on atomic friction. Phys. Rev. Lett. 87, 174301 (2001).
Igarashi, M., Natori, A. & Nakamura, J. Size effects in friction of multiatomic sliding contacts. Phys. Rev. B 78, 165427 (2008).
Benassi, A., Vanossi, A. & Tosatti, E. Nanofriction in cold ion traps. Nature Commun. 2, 236 (2011).
Cetina, M. et al. One-dimensional array of ion chains coupled to an optical cavity. New J. Phys. 15, 053001 (2013).
Pruttivarasin, T., Ramm, M., Talukdar, I., Kreuter, A. & Häffner, H. Trapped ions in optical lattices for probing oscillator chain models. New J. Phys. 13, 075012 (2011).
Mandelli, D., Vanossi, A. & Tosatti, E. Stick–slip nanofriction in trapped cold ion chains. Phys. Rev. B 87, 195418 (2013).
Enderlein, M., Huber, T., Schneider, C. & Schaetz, T. Single ions trapped in a one-dimensional optical lattice. Phys. Rev. Lett. 109, 233004 (2012).
Linnet, R. B., Leroux, I. D., Marciante, M., Dantan, A. & Drewsen, M. Pinning an ion with an intracavity optical lattice. Phys. Rev. Lett. 109, 233005 (2012).
Acknowledgements
We acknowledge support from the NSF-funded Center for Ultracold Atoms. D.G. and A.B. acknowledge funding from NSERC.
Author information
Authors and Affiliations
Contributions
D.G., A.B. and V.V. designed the experiments. D.G., A.B. and I.C. collected and analysed data. All authors discussed the results and contributed to the manuscript preparation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 917 kb)
Rights and permissions
About this article
Cite this article
Gangloff, D., Bylinskii, A., Counts, I. et al. Velocity tuning of friction with two trapped atoms. Nature Phys 11, 915–919 (2015). https://doi.org/10.1038/nphys3459
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3459
This article is cited by
-
Coherent control of \(^{171}\mathrm{Yb}^{+}\) ion qubit states and thermometry using motional decoherence
Journal of the Korean Physical Society (2021)
-
Probing nanofriction and Aubry-type signatures in a finite self-organized system
Nature Communications (2017)
-
Observation of Aubry-type transition in finite atom chains via friction
Nature Materials (2016)
-
Microscopic friction emulators
Nature (2015)