Main

Quantum correlations are particularly important in the context of quantum simulation12,13,14, quantum phase transitions15,16, as well as for quantum computation17. In these experiments, one typically strives to study quantum many-body dynamics in high-dimensional Hilbert spaces. However, it is precisely in these complex systems where it becomes increasingly difficult to experimentally detect quantum correlations because standard methods such as full state tomography are impractical18. Therefore, it seems natural to restrict oneself to measurements of a smaller controllable subsystem19. Similarly, in quantum communication protocols, each party has access only to its part of the shared correlated state but may want to confirm the presence of quantum correlations locally3. All these situations can be described in the framework of a well-controlled open quantum system in contact with an inaccessible environment6.

Initial system–environment correlations can significantly change the dynamics of open systems6,7,8,9. The standard master equation approach to open systems assumes an initial state with vanishing total correlations, which may not be appropriate unless a product state is explicitly prepared20,21. Moreover, the information flow between the system and its environment and the corresponding degree of non-Markovianity is closely related to the presence of correlations9,22,23,24.

The present experiment follows a recently proposed protocol to detect nonclassical system–environment correlations of an arbitrary, unknown state by accessing only the open system10,11. The correlations are revealed through their effect on the open system dynamics. The protocol does not require any knowledge about the environment or the nature of the interaction, making it applicable to a wide range of scenarios where only partial access to a possibly correlated dynamical system is granted.

Previous experiments have detected correlations between system and environment in photonic systems20,21, without distinguishing between classical and quantum correlations. In this work, we identify the detected correlations as quantum discord. A definition for this particular notion of quantum correlations will be given in the context of the local detection protocol. For pure total states, quantum discord is equivalent to entanglement. Quantum discord is considered a resource for certain quantum information processing protocols based on mixed states where little or no entanglement is needed2,25,26.

The local detection protocol is outlined in Fig. 1. It is based on the comparison of the time evolution of the locally accessible system with and without quantum correlations between the system and its environment. Any difference in these time evolutions proves the presence of quantum correlations. The first step consists in performing state tomography of the locally accessible part of the total state ρ, yielding the reduced density matrix ρS = TrEρ of the system, where TrE denotes the partial trace over the environment6. On the basis of the eigenvectors |i〉 of we define the dephasing operation Φ as

This operation acts only on the accessible part of the state ρ, creating a reference state , where denotes the identity operation on the environment. The local dephasing operation is the central element of the detection process: it is implemented on a strictly local level but erases all quantum correlations between the system and the environment. To see this, we first note that this operation does not change the reduced density matrices of either the system or the environment11. The only difference between the states ρ and ρ′ is the absence of certain coherences in ρ′. These coherences constitute the quantum correlations in ρ according to the notion of quantum discord2. Hence, the state ρ contains quantum discord if and only if . The next step of the protocol consists of subjecting both states ρ and ρ′ to the same global unitary time evolution U(t). We then compare how the subsystem evolves in time. More precisely, if the subsystem time evolution without quantum correlations,

differs from the original time evolution,

one has detected non-vanishing quantum discord in the state ρ.

Figure 1: Outline of the local detection protocol.
figure 1

The outer box represents the total system, which is connected to its accessible local subsystem in the grey box through the partial trace operation TrE (dashed arrows). First, the accessible part ρS of the unknown state ρ is measured. The eigenbasis of ρS determines the local dephasing operation . Local dephasing removes the quantum correlations of ρ and creates a reference state ρ′. The two states have the same initial reduced density matrices, ρS = ρ′S. Now, both total states ρ and ρ′ are subject to the same unitary time evolution U(t). A different time evolution in the open system, that is , reveals the presence of quantum correlations in ρ (ref. 10).

Full size image

We apply the described protocol to a trapped ion system, consisting of an electronic two-level system coupled to a single mode of the ion’s motion. The electronic state of the ion represents the open system, whereas we regard the ion motion as a simple environment. Using this model system allows us to establish quantum correlations in a well-controlled manner and, thus, to assess the performance of the protocol accurately.

For our experiments, we trap a single 40Ca+ ion in a linear Paul trap. We encode a qubit in the two-level system consisting of the states |g〉 = |S1/2,mj = −1/2〉 and |e〉 = |D5/2,mj = −5/2〉, coherently manipulated with narrow band laser light at 729 nm, see Fig. 2. The frequencies (ωx,ωy,ωz) of the harmonic ion motion are 2π×(2.8,2.6,0.2) MHz.

Figure 2: Description of open system and environment.
figure 2

The left side depicts the relevant electronic levels of 40Ca+. We use a narrow linewidth 729 nm laser on the quadrupole transition between the |g〉 = |S1/2,mj = −1/2〉 and |e〉 = |D5/2,−5/2〉 states for qubit manipulations. A magnetic field of 100 μT along the axial direction lifts the degeneracy of different Zeeman levels. The ion is optically pumped into |g〉. State readout and Doppler cooling are performed using the 397 nm transition27. An additional blue-detuned laser on the same transition implements the local dephasing operation via the AC-Stark effect. Detuning the 729 nm laser to the blue sideband couples the electronic state to the ion’s motion, described by a quantum harmonic oscillator.

Full size image

Correlations between the electronic state and the motion can be created by detuning the laser from the qubit transition to one of the motional sidebands. In particular, choosing a blue detuning of +ωx generates the anti-Jaynes–Cummings Hamiltonian (see Supplementary Information)27

We have introduced the effective Rabi frequency Ωn, eigenstates |n〉 of the harmonic oscillator, σ+ = |e〉〈g| and ℏ = h/2π, where h is Planck’s constant. This Hamiltonian couples the pairs of states |g,n〉 and |e,n+1〉.

Using a combination of Doppler and sideband cooling, we prepare thermal states of motion, resulting in the total state

with , where denotes the mean occupation number of the motional state27. A correlated state ρ(t0) is then created by driving the blue sideband transition for a time t0. We first determine the density matrix of the local state, that is the qubit, ρS = TrEρ(t0), see Fig. 3. As expected from theoretical considerations, we find that the eigenbasis of the qubit is given by the computational basis {|g〉,|e〉} for all t0 (see Supplementary Information). Hence, local dephasing (equation (1)) must be implemented in this basis. To this end, we shift the ground state energy by h×40 kHz with an AC-Stark shift generated by laser light detuned by +400 GHz with respect to the S1/2–P1/2 transition. By varying the interaction time, we generate different phase shifts between |e〉 and |g〉. We sample over different phases between 0 and 2π such that the phase factors average to zero, effectively removing all coherences in the basis {|g〉,|e〉}. We show in the Supplementary Information that this method can achieve dephasing in an arbitrary basis if it is combined with two unitary rotations.

Figure 3: Local detection of qubit-motion quantum correlations.
figure 3

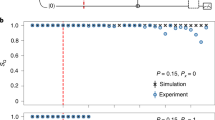
a, The experimental sequence is illustrated. b, After a preparation sideband pulse of duration t0, state tomography yields the reduced density matrix ρS of the initial state (absolute values plotted). d,e, The evolution of the excited state population 〈e|ρS(t)|e〉 is observed under the subsequent sideband interaction of duration t1 (plotted in red). This evolution is compared to a second realization where the local dephasing operation (equation (1)) is applied in between the two pulses (blue). Comparisons of the time evolution of the excited state population are shown for a Doppler-cooled state (; d) and a sideband-cooled state (; e). Even though the initial reduced density matrix is the same with and without dephasing (b,c), the time evolution is noticeably different. We fit 〈e|ρS(t)|e〉 to a theoretical model which is outlined in the Supplementary Information (red/black dots and lines). The obtained fit parameters determine the predicted evolution for the dephased state (dashed blue line) which is compared with the measured data (blue dots). The error bars indicate the statistical errors , where n = 1,000 is the number of measurements for each data point.

Full size image

Figure 3b,c shows the density matrix before and after the dephasing and confirm that this operation leaves the local state unaffected. The estimated scattering rate is less than 10−3 photons during the dephasing and, thus, also the motional state remains unaltered (see Supplementary Information for details).

To detect the presence of quantum correlations, we compare the dynamics of the qubit with and without dephasing. Figure 3d,e compares the time evolution of the excited state population under blue sideband interaction for different temperatures of the environment over a time interval t1. We find pronounced differences in the open-system dynamics of the qubit, demonstrating the presence of quantum discord in the initial state. The signature of the correlations is more dominant when the ion was prepared in a nearly pure state by sideband-cooling (Fig. 3e). If the total system is known to be in a pure state, quantum correlations in form of entanglement can be detected by observation of mixed states in the open system1. However, the presented method does not require any assumptions about the total state and works well even for thermal states of higher temperature (as shown in Fig. 3d). The evolution is in good agreement with the theoretical prediction for both temperature regimes.

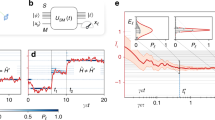
We measure the signature of the correlations on the reduced dynamics as a function of preparation duration t0 and detection duration t1, see Fig. 4. We quantify the difference in the time evolution by means of the trace distance of the reduced states,

where denotes the trace norm and d(t0,t1) = 〈e|ρS(t0+t1)−ρ′S(t0+t1)|e〉 the difference of populations in the excited state.

Figure 4: Open-system trace distance for environmental states of different temperatures.
figure 4

(Left side: , right side: .) The contour plots show the theoretical prediction for the trace distance D(ρS(t0+t1),ρ′S(t0+t1)) of the open-system states, which serves as a witness for quantum correlations. The measured distance evolution after different preparation durations is shown in comparison with the theoretical curve in the subfigures. The time axis is scaled by the characteristic sideband interaction strength for the ground state η Ω, with η = 0.04 being the Lamb-Dicke factor and Ω≈2π×100 kHz the Rabi frequency of the carrier. The black lines are the theoretical predictions for the parameters obtained by fitting 〈e|ρS(t)|e〉 for each of the preparation durations. The contour plot is generated with the average parameters of the individual measurements. In the sideband-cooled state, the time evolution is mostly determined by the ground state contribution. This makes the time evolution more periodic, as opposed to the case of a Doppler-cooled state when multiple motional states with different Rabi frequencies contribute. The error bars report statistical errors of 1,000 measurements for each point.

Full size image

As the only difference between the original state ρ(t0) and the dephased state ρ′(t0) is the lack of quantum discord in ρ′(t0), we can use

to quantify the quantum correlations of ρ(t0) (ref. 28). Owing to the contractivity property of the trace distance3, the local distance (equation (2)) provides, for every value of t1, a lower bound for the quantum correlations (ref. 11). The best lower bound is found by maximizing the local distance over all values of t1:

As shown in Fig. 5, we find the experimentally obtained lower bound remarkably close to the actual quantum correlations for both environmental temperatures (see Supplementary Information for further details).

Figure 5: Maximum of the local distance and quantum correlations at the dephasing time.
figure 5

The maximum of the local distance provides a lower bound to the amount of quantum correlations present at the time the dephasing was employed, see equation (3). For a state with the average properties of the four sideband-cooled realizations () we find the lower bound almost reaching the actual value of the quantum correlations. Even for the average Doppler-cooled state (), the experimentally obtained maximal distance provides a reasonably tight lower bound for the quantum correlations and in most cases reaches the theoretical limit, which is obtained by numerical simulations. For the low-temperature state the theoretical maximum is not attained within the measured range for the detection time, which is shown in Fig. 4. The error bars contain statistical errors (y axis) and the error for the fit of the Rabi frequency (x axis).

Full size image

The techniques developed in this work can be broadly applied to unknown states of open systems interacting with an arbitrary environment. In this context, it is important to note that for strong system–environment couplings initial correlations are known to have a substantial influence on the open system dynamics even for large, realistic environments with an infinite number of degrees of freedom and a continuous spectral density6,29.

We foresee the application of this method to characterize quantum phase transitions through the observation of quantum correlations15,16 in systems where full access to the quantum state is not feasible, for example large trapped-ion crystals30 or cold atoms in optical lattices19 (see Supplementary Information for further details). Furthermore, we believe that the demonstrated scheme will be helpful in experimentally identifying situations where the standard master equation treatment will fail to describe an open system in contact with an inaccessible or even unknown environment.