Abstract
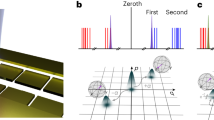
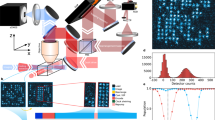
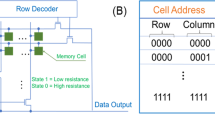
Shor and Grover demonstrated that a quantum computer can outperform any classical computer in factoring numbers1 and in searching a database2 by exploiting the parallelism of quantum mechanics. Whereas Shor's algorithm requires both superposition and entanglement of a many-particle system3, the superposition of single-particle quantum states is sufficient for Grover's algorithm4. Recently, the latter has been successfully implemented5 using Rydberg atoms. Here we propose an implementation of Grover's algorithm that uses molecular magnets6,7,8,9,10, which are solid-state systems with a large spin; their spin eigenstates make them natural candidates for single-particle systems. We show theoretically that molecular magnets can be used to build dense and efficient memory devices based on the Grover algorithm. In particular, one single crystal can serve as a storage unit of a dynamic random access memory device. Fast electron spin resonance pulses can be used to decode and read out stored numbers of up to 105, with access times as short as 10-10 seconds. We show that our proposal should be feasible using the molecular magnets Fe8 and Mn12.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Shor, P. in Proc. 35th Ann. Symp. Foundations of Computer Science (ed. Goldwasser, S.) 124–134 (IEEE Computer Society Press, Los Alamitos, 1994).
Grover, L. K. Quantum computers can search arbitrarily large databases by a single query. Phys. Rev. Lett. 79, 4709–4712 (1997).
Lloyd, S. Quantum search without entanglement. Phys. Rev. A 61, R010301-1–010301-4 (1999).
Ekert, A. K. & Jozsa, R. Quantum computation and Shor's factoring algorithm. Rev. Mod. Phys. 68, 733–753 (1996).
Ahn, J., Weinacht, T. C. & Bucksbaum, P. H. Information storage and retrieval through quantum phase. Science 287, 463–465 (2000).
Thiaville, A. & Miltat, J. Magnetism: small is beautiful. Science 284, 1939–1940 (1999).
Thomas, L. et al. Macroscopic quantum tunnelling of magnetization in a single crystal of nanomagnets. Nature 383, 145–147 (1996).
Friedman, J. R., Sarachik, M. P., Tejada, J. & Ziolo, R. Macroscopic measurement of resonant magnetization tunneling in high-spin molecules. Phys. Rev. Lett. 76, 3830–3833 (1996).
Sangregorio, C., Ohm, T., Paulsen, C., Sessoli, R. & Gatteschi, D. Quantum tunneling of the magnetization in an iron cluster nanomagnet. Phys. Rev. Lett. 78, 4645–4648 (1997).
Wernsdorfer, W., Sessoli, R., Caneschi, A., Gatteschi, D. & Cornia, A. Nonadiabatic Landau-Zener tunneling in Fe8 molecular nanomagnets. Europhys. Lett. 50, 552–558 (2000).
Fitzgerald, R. Pulse shaping improves efficiency of soft X-ray harmonic generation. Phys. Today 53, 24–28 (2000).
Cohen-Tannoudji, C., Diu, B. & Laloë, F. Quantum Mechanics Vol. 2, 1323–1339 (Wiley, New York).
Barra, A. L., Gatteschi, D. & Sessoli, R. High-frequency EPR spectra of a molecular nanomagnet: Understanding quantum tunneling of the magnetization. Phys. Rev. B 56, 8192–8198 (1997).
Mirebeau, I. et al. Low-energy magnetic excitations of the Mn12-acetate spin cluster observed by neutron scattering. Phys. Rev. Lett. 83, 628–631 (1999).
Leuenberger, M. N. & Loss, D. Spin tunneling and phonon-assisted relaxation in Mn12-acetate. Phys. Rev. B 61, 1286–1302 (2000).
Leuenberger, M. N. & Loss, D. Incoherent Zener tunneling and its application to molecular magnets. Phys. Rev. B 61, 12200–12203 (2000).
Acknowledgements
We thank G. Salis and J. Schliemann for useful comments. This work has been supported in part by the Swiss NSF and by the European Union Molnanomag network.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Leuenberger, M., Loss, D. Quantum computing in molecular magnets. Nature 410, 789–793 (2001). https://doi.org/10.1038/35071024
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/35071024
This article is cited by
-
Vibronic effects on the quantum tunnelling of magnetisation in Kramers single-molecule magnets
Nature Communications (2024)
-
A hybrid-qudit representation of digital RGB images
Scientific Reports (2023)
-
A trivalent 4f complex with two bis-silylamide ligands displaying slow magnetic relaxation
Nature Chemistry (2023)
-
Magnetic molecules lose identity when connected to different combinations of magnetic metal electrodes in MTJ-based molecular spintronics devices (MTJMSD)
Scientific Reports (2023)
-
A near-linear lanthanide complex that displays magnet-like behaviour
Nature Chemistry (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.