Introduction

The mapping of multiple quantitative trait loci (QTLs) is typically framed as a regression problem, where the phenotypic trait values, , of n genotyped individuals are regressed on their genotypes at p candidate maker loci (for example, Haley and Knott, 1992; Sen and Churchill, 2001). More specifically, the mapping model has the form

where α is the intercept, xij is the genotype code of individual i at locus j (j=1, …, p), bj is the genetic effect of locus j and ei (i=1, …, n) are independent and identically distributed (i.i.d.) residual errors assumed to be Gaussian with mean 0 and variance σ02. Here, attention is restricted to controlled crosses such as backcross or double-haploid progeny with only two possible genotypes at any locus, and xij is coded as 0 for one genotype and 1 for the other. In matrix notation, (1) becomes

where 1n is an n-vector of ones, b=(b1, …, bp)T, e=(e1, …, en)T and X is the n × p design matrix comprising the genotype profiles of the p loci.

When marker effects are assumed to be strictly additive (that is, no dominance effect involved) as in (1), the phenotypic variance σy2 may be partitioned into the genetic variance (VG) and the residual variance (σ02). The expression of the genetic variance of a QTL depends on the assumed genotype coding. For example, the genetic variance for a biallelic QTL in an F2 population under the genotype coding AA=1, AB=0 and BB=−1 is given by , where is the estimated genetic effect of the QTL of interest, whereas p and q are the allele frequencies, with q=(1−p). When p=q=0.5, the genetic variance of a QTL is . In a double-haploid or a backcross population, under the genotype coding 1/−1 for the two possible genotypes, and under the genotype coding 1/0 which is used here, with p and q=1−p denoting the frequencies of the two possible genotypes (for example, AA/BB in double haploids, and AA/AB in backcross) at the focal locus. Hence, in a double-haploid or a backcross population under the genotype coding 1/0 when p=q=0.5 (for example, Xu, 2003a). For more details on the derivation of the genetic variance with regard to the assumed genotype coding, see Supplementary Appendix A. If denotes the empirical phenotypic variance estimated from the data, then the extent to which phenotypes are determined by the particular QTL transmitted from the parents is measured by the ratio , known as QTL-heritability in the narrow sense, or simply QTL-heritability (Falconer and Mackay, 1996, pp. 123–127).

The QTL-heritability concept takes into account the allele frequencies at QTLs, and is more relevant in outbred populations. However, it provides a practical means of individually evaluating the importance of QTLs even in experimental crosses where allele frequencies are determined by the crossing design, and will be used here for this purpose.

QTL mapping models based on dense sets of molecular markers are typically saturated, implying that the number of candidate loci exceeds the sample size (the number of genotyped individuals). On the other hand, strong correlations among dense marker genotypes induce multi-collinearity issues (Xu, 2003b). Using saturated models and/or models involving collinear predictors, traditional estimation methods such as maximum likelihood estimation are prone to over-fitting.

It is, however, widely recognized that the genetic bases of quantitative traits are typically sparse, in the sense that most of the candidate loci have a weak or no effect on the phenotype (for example, Xu, 2003b; O'Hara and Sillanpää, 2009). Therefore, enforcing model sparsity has emerged as a legitimate means to avoid over-fitting, while improving the model's interpretability and enhancing its predictive performance in gene mapping studies. Several methods have been proposed for sparse model representation under both the classical (frequentist) and Bayesian approaches. These can be classified roughly into two categories, namely, variable selection and regularization or shrinkage methods.

Variable selection methods entail the idea of excluding the presumably redundant predictors from the model. Classical forward selection, backward elimination and stepwise selection techniques (Broman, 2001; Broman and Speed, 2002), as well as Bayesian spike-and-slab approaches such as stochastic search variable selection (George and McCulloch, 1993; Yi et al., 2003; Mutshinda et al., 2009, 2011) or Bayes B (Meuwissen et al., 2001), fit into this category.

Regularization or shrinkage methods, on the other hand, attempt to estimate all regression coefficients simultaneously, but involve a mechanism for automatically shrinking the effects of redundant predictors (spurious effects) towards 0.

Classical shrinkage methods such as ridge regression (Hoerl and Kennard, 1970; Whittaker et al., 2000) and the absolute shrinkage selection operator (LASSO; Tibshirani, 1996) are essentially penalized maximum likelihood techniques. There, model sparsity is achieved by imposing on the negative log-likelihood (the cost function to be minimized) a penalty function intended to promote smaller parameters values. Different shrinkage methods are determined by the form of the penalty function. For example, ridge regression and LASSO penalize the L2 and L1 norms of the regression coefficient vector, respectively.

In Bayesian shrinkage analysis (for example, Xu, 2003b; Yi and Xu, 2008; Mutshinda and Sillanpää, 2010; Sun et al., 2010), model sparsity is achieved through the use of the so-called sparsity-inducing priors. These are typically defined to be centred on 0, with no thinner than Gaussian tails. More importantly, when each regression coefficient (marker effect) is assigned its own variance parameter, adaptive shrinkage is allowed to take place through differences in the magnitudes of these idiosyncratic variances. The idea is to give larger penalties (corresponding to smaller variances) to unimportant variables to heavily shrink their associated coefficients, and vice versa (for example, Figueiredo, 2003; Xu, 2003b). This feature allows Bayesian shrinkage models to handle a number of predictors many times larger than the sample size (Xu, 2003b; Hoti and Sillanpää, 2006; Zhang et al., 2008).

It has been well-recognized as a major problem in Bayesian shrinkage analysis of large-scale associations that the prior setting for marker effects (both the tail-decay rate and the parameter setting) much affects the effectiveness of QTL mapping and the prediction of genomic breeding values (for example, Gianola et al., 2009). For example, a centred normal prior leaves the regression coefficients (marker effects) non-zero. By contrast, a centred Laplacian or double exponential prior can shrink some of the spurious effects to 0, owing to its sharp peak at the mode, while allowing the effect sizes of important predictors to take values much larger than 0 as a result of its heavy-tailedness. These two attributes allow the Bayesian shrinkage model under a Laplacian prior to combine parameter shrinkage with variable selection. This explains the increasing interest in the LASSO-type penalties.

In practice, the shape of shrinkage priors is routinely preset to be, for instance, of the Gaussian, Laplacian or Student-t forms, with no regard for the range of plausible alternatives, and the fact that the most suitable shape may depend on the data at hand.

In this paper we introduce the shape-adaptive shrinkage prior (SASP) approach to address this issue, focusing on QTL mapping in experimental crosses. The underlying principle of the SASP approach is to impose on each regression parameter a hierarchical prior involving a generalized Gaussian (GG) distribution at the lowest level. The shape parameter of the GG is set as a free parameter to be estimated alongside the other model parameters to suitably adjust the tail decay of the priors for the data set at hand.

Materials and methods

Before delving into details regarding the prior specification and model fitting issues, it may be instructive to reconsider the GG distribution.

The GG distribution

The probability density function of a random variable X having a GG distribution is given by

(Niehsen, 1999; Mitra and Sicuranza, 2001), where μ∈ℜ is a location parameter representing the mean of the distribution and v>0 is the shape parameter, which determines the rate of tail decay. For 0<v<2, the tails decay more slowly than those of the normal distribution, resulting in heavier-tailed distributions. δ>0 is the scale parameter relating to the variance of X through , and Γ(.) denotes Euler's Gamma function: , z>0.

The GG family encompasses a continuum of distributional shapes, with the Laplacian, the Gaussian and the uniform distributions arising as particular cases when v=1, v=2 and v → ∞, respectively. Henceforth, GG (v, δ) denotes the probability density function of a GG distribution centred on 0, with shape parameter v and scale parameter δ.

Hierarchical Bayesian specification of the model

We adopt a hierarchical Bayesian modelling approach (Gelman et al., 2003). Hierarchical modelling is a conceptual and philosophical approach to model construction, with proven practical advantages regardless of whether one is adopting a Bayesian approach or not (for example, Royle and Dorazio, 2008). Under the Bayesian framework, all unknown quantities are assigned prior distributions. The joint prior of the model parameters is combined, through Bayes formula, with the likelihood to produce the posterior distribution, that is, the conditional distribution of the parameters given the data. Bayesian inferences are made in terms of probability statements about the unknown parameters or yet unobserved data (prediction), with regard to the posterior distribution.

A hierarchical Bayesian model is a Bayesian model where the prior distributions are specified in a hierarchy: parameters in the likelihood have priors, some of which may also have priors (hyper-priors). The parameters of hyper-priors (called hyper-parameters) may in turn have priors etc., with the process coming to an end when no more priors are introduced. The HB model specification makes it easier to exploit the structural links between different pieces of data by expressing complex joint distributions as products of simple conditional distributions, and adopting prior specifications that convey substantive knowledge of the underlying mechanisms. The likelihood for our model (1) is

As noted earlier, we proceed by imposing independent GG priors on each marker effect bj for (j=1, …, p). More specifically, we let , where . The hyper-parameters λ and ηj are, respectively, intended to control the model sparsity level and the degree of shrinkage specific to locus j (cf. Mutshinda and Sillanpää, 2010).

After suitable priors p(α), p(σ02) and p(v) have been specified for the intercept, the residual variance and the shape or tail-decay parameter of the GG distribution, the joint prior of all model parameters and their joint posterior are, respectively, given by

It goes without saying that the high-dimensional posterior distribution (4) does not have a familiar form. However, as we discuss in the section on model fitting issues below, we can simulate from it through sampling-based methods such as Markov chain Monte Carlo (MCMC) methods (Gilks et al., 1996; Gelman et al., 2003).

Model fitting issues

As already pointed out, the model fitting to the data can be performed by MCMC simulation methods through standard Bayesian freeware such as BUGS (WinBUGS/OpenBUGS; Spiegelhalter et al., 2003; Thomas et al., 2006). The only stumbling block seems to be simulation from the GG distribution. This, however, turns out to be straightforward after a suitable variable transformation (that is, change of variables). More briefly, if we let , then a sample can be obtained as , where and . The factor is introduced to make positive and negative values of bj equally likely, given that the GG distribution is symmetric and supported on the entire real line. Supplementary Appendix B provides more details on this issue. This simulation scheme can easily be implemented in BUGS (see Supplementary Appendix C).

Simulation studies

We conducted two simulation studies to investigate the performance of our model, using the extended Bayesian LASSO (EBL; Mutshinda and Sillanpää, 2010) as benchmark for comparison. Simulation studies I and II were, respectively, based on real-world barley (Hordeum vulgare L.) marker data and on a synthetic dense marker map simulated through the WinQTL Cartographer 2.5 program (Wang et al., 2006). The empirical statistical power (ESP) of detecting true QTLs can be evaluated in replicated data analysis by the proportion of the replicates in which the estimated QTL effect size exceeds the empirical significance threshold used to declare QTLs (see the sections below). The ESP relates to the type-II error, β, as β=1−ESP.

Xu (2010) argued that the effect of a QTL failing to be detected can be picked up by a neighbouring locus. Along his lines, we consider three consecutive loci with a true QTL in the middle as QTLs. All computations were performed on an AMD Turion X2 Dual, equipped with a 64-bit operating system with a 2.10 GHz processor and 4 GB of RAM.

Results

Simulation study-I: Our first simulation study is based on a real-world barley marker data set from the North American Barley Genome Mapping project (Tinker et al., 1996). This data set comprises 127 biallelic markers on 145 doubled-haploid lines for which the phenotype ‘number of days to heading averaged over 25 environments’ was available from the original data. The markers span seven chromosomes, with an average distance of 10.5 cM between consecutive markers. The few missing genotypes were filled in with random draws from Bernoulli(0.5) before the analysis. The phenotypic trait values were simulated under sparse underlying biology with only four QTLs (QTL1, QTL2, QTL3 and QTL4), namely, at loci 4, 25, 50 and 65, with respective effects set to 2.5, −2.5, 4 and −4. Loci are here identified by their marker indices (for example, 4, 25, 50 and 65). The intercept was set to 0 without loss of generality, and the residual variance was set to 2, yielding a rough heritability of 0.80. The simulated QTL-heritabilities of QTL1, QTL2, QTL3 and QTL4 were, respectively, 0.14, 0.14, 0.35 and 0.35 under the assumption that p=q=0.5.

We generated 50 replicated data sets and analysed each replicate using the SASP-based Bayesian shrinkage model and the EBL selected as a benchmark for comparison. The choice for EBL as the reference line was motivated by the fact that the latter makes a clear distinction between model sparsity and parameter shrinkage, and arises as a particular case of the SASP-based model when the shape parameter is fixed to 1.

The model fitting was performed by MCMC simulation through OpenBUGS (see BUGS code in SOM; Supplementary Appendix C) using the following fairly uninformative priors: ; , , bearing in mind that 0<v<2 is required for inducing fatter-than-normal tails. We set the prior of λ to be , which has an expected value 5 and a quite large (50) variance. Finally, we assume that independently for , where I(.) denotes the indicator function. The prior mode of ηj is 1, and p(ηj) is properly truncated to steer clear of negative values. Updating of λ to the adequate model sparsity level will push the shrinkage factors ηj towards lower values than 1 for genuine QTLs effects and towards larger values for spurious effects to achieve adaptive shrinkage. As the support of ηj is a priori unbounded from above, ηj can take larger values and effectively prune redundant predictors from the model.

Initially, we ran 20 000 iterations of two MCMC chains starting from dispersed initial values to assess the mixing of the MCMC. The chains seemed to reach their target distribution after about 500 iterations. The computation time was higher for the SASP relative to the EBL, owing presumably to the convoluted hierarchical priors involved in the former. The 20 000 iterations of two chains took 3000 s for the EBL versus 10 000 s for the SASP model.

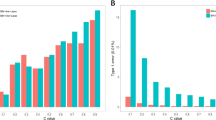
We used the phenotype permutation method (Churchill and Doerge, 1994) to determine the empirical significance thresholds for distinguishing QTLs from non-QTLs under each model. This procedure consists of the following three steps: (1) Randomly shuffling the data (N times, say) by pairing one individual's genotypes with another's phenotype, in order to simulate data sets with the observed linkage disequilibrium structure under the null hypothesis of no intrinsic genotype-to-phenotype relationship; (2) performing mapping analysis and obtaining the value of a suitable test statistic, for example, the maximum (absolute) effect size, for each of N shuffled data sets. This yields an empirical distribution F of the test statistic under the null hypothesis; (3) selecting the 100 × (1−α) percentile of F as a critical threshold for declaring QTLs, where 0<α<1 is chosen to control the type-I error (false discovery rate). We used N=50 phenotype permutations and for each permuted data set, we ran 6000 iterations of a single MCMC chain, discarding the first 2000 samples as burn-in and thinning the remainder to each fifth sample. The significance thresholds, T, for QTL effect sizes based on a significance level α=0.10 for the EBL and the SASP-based model are shown as dashed horizontal lines in Figure 1. There, the vertical needles represent the estimated QTL effects as posterior means averaged over 50 replications under the two models, and the solid diamonds indicate the true QTL effects.

Figure 1
figure 1

True values (grey diamonds) and posterior means of marker effects (vertical bars) averaged over 50 replicated data sets under the EBL (top) and the SAP approach (bottom) plotted against the marker indices, for simulations based on the barley marker data. The dashed horizontal lines indicate the permutation-based QTL significance thresholds. EBL, extended Bayesian LASSO; QTL, quantitative trait locus; SASP, shape-adaptive shrinkage prior.

Full size image

Table 1 shows the true values and the posterior means averaged over 50 replicated data sets for the model parameters that are common to the EBL and the SASP-based model.

Table 1 True parameter values and the posterior means averaged over 50 replicated data sets and associated standard errors (s.e.s) under the EBL and the SASP approach, for simulations based on barley marker data
Full size table

For the SASP-based model, the range of the posterior mean of the shape parameter over replicates was [0.59, 1.12], with a median value of 0.85, implying a relatively stronger shrinkage than under the EBL. This resulted in a clearer separation between genuine QTL effects and spurious ones under the SASP-based model as can be seen from Figure 1. On the other hand, the prior specification adopted for the locus-specific shrinkage factors ηj seemed to effectively prevent true QTL effects from strong shrinkage, thereby allowing them to be estimated with reasonable accuracy as suggested by the results depicted in Figure 1. The estimated QTL-heritabilities of QTL1, QTL2, QTL3 and QTL4 averaged over the 50 replicated data sets were, respectively, 0.11, 0.10, 0.28 and 0.30 for the EBL and 0.12, 0.11, 0.31 and 0.32 for the SASP-based model under the assumption that p=q=0.5, with the SASP-based values being slightly closer to the true values than their EBL counterparts.

All true QTLs were detected in all replicated analyses under both models, implying an empirical statistical power of roughly 100%. Adjacent loci to true QTL positions were also occasionally selected under the EBL. We conducted a second simulation study to investigate the performance of our model in oversaturated models with dense and highly correlated markers.

Simulation study-II: The second simulation study was based on a synthetic dense marker map simulated through the WinQTL Cartographer 2.5 programme (Wang et al., 2006), and involving 102 markers for 50 backcross progeny (more than twice more markers than individuals). The marker data set used here is a random sample from a data set used by Sillanpää and Noykova (2008). It comprises three chromosomes, with 34 evenly spaced markers on each chromosome, and just 3 cM between consecutive markers. The phenotypic values were simulated from a sparse model with only four QTLs (QTL1, QTL2, QTL3 and QTL4), with the same positions and effects as in Simulation study-I. The intercept was again set to 0 and the residual variance to 1, yielding a rough heritability of 0.80. The simulated QTL-heritabilities of QTL1, QTL2, QTL3 and QTL4 were, respectively, 0.15, 0.15, 0.38 and 0.38.

The model fitting to the data was performed by MCMC through OpenBUGS using the same prior specification as in Simulation study-I. We analysed a couple of replicated data sets, running 10 000 iterations of a single chain, discarding the first 3000 as burn-in and thinning the remainder to each tenth sample. The running times for the EBL and the SASP-based model were, respectively, 1017 s and versus 9000 s.

We noticed that, with dense markers, the genetic effects were usually broken up over nearby loci to actual QTL positions with varying magnitudes not only in different replicates but also in different model runs using the same data set, as a result of multi-collinearity. This makes it unreasonable to average the results over replicated data sets. It is however worth pointing out that the estimated genetic effect of each of nearby loci was in general relatively small, implying negligible QTL-heritabilities when the actual QTL effect was shared by multiple loci.

Figure 2 shows a typical plot of the posterior means of the QTL effects against the marker indices under the EBL and the SASP-based models. The dashed lines indicate the empirical QTL significance levels based on 50 phenotype permutations, with same number of iterations as in Simulation study-I.

Figure 2
figure 2

Posterior mean QTL effects plotted against the marker indices for the EBL and the SASP approach for a single data set under the simulated dense marker map. The grey diamonds represent ‘true’ QTL effects and the dashed horizontal lines indicate the permutation-based QTL significance thresholds. EBL, extended Bayesian LASSO; QTL, quantitative trait locus; SASP, shape-adaptive shrinkage prior.

Full size image

The range of v for the SASP-based model was 0.56–1.22. A relatively stronger shrinkage for spurious effects was observed under the SASP-based model as compared with that under the EBL. The estimates of spurious effects were typically two orders of magnitude lower than those of genuine QTL effects under the SASP-based approach, making the separation between genuine QTL effects and spurious effects clearer (Figure 2).

The empirical statistical power was roughly 100% for QTL3 and QTL4 under the two models. For each of the two other loci, namely, QTL1 and QTL2, the ESP under the EBL and the SASP-based model were, respectively, 91 and 96%.

It is perceptible from Figure 2 that some of the estimated QTL effect sizes may be far below their true values, as a result of collinearity among markers. Buhlmann and Meier (2008) pointed out that, when viewing the shrinkage mechanism as a variable filtering method, an additional step may be necessary to go from the shrinkage estimates to the true model. This additional step is what we refer to as accurate re-estimation of the genetic effects of the selected QTL loci. We discuss a procedure for doing this in the following section.

Accurate re-estimation of QTL effects

The shrinkage-induced bias on the estimated effects of the selected QTLs can be alleviated by re-estimating them from the so-called ‘relaxed model’. This is nothing but the mapping model limited to the low-dimensional subspace of the selected markers, with no shrinkage imposed on their effects, that is, under diffuse (that is, fairly flat) priors such as i.i.d. centred Gaussians with large variance. By doing so, the estimated effects of the selected loci are adjusted in the direction of the least squares solution. This relaxed estimation can be implemented handily without having to modify the original marker data as follows: Let be a vector of indicators with γj=1 when locus j is selected as QTL, and γj=0 otherwise, and let be a vector of auxiliary Gaussian variables. To implement the relaxed estimation, it suffices to replace b in Equation 2 by the point-wise vector multiplication β•γ, with i.i.d. zero-mean diffuse Gaussians placed on the component of β. This can be easily achieved using BUGS for MCMC sampling (see Supplementary Appendix D).

After the re-estimation step, the search for additional QTLs can be attempted by re-fitting the shrinkage model barring the already selected QTLs and pre-conditioning on their effects, that is, deducting their effects from the phenotypic data (phenotype adjustment). The exclusion of the already selected loci can also be conveniently implemented through the indicator-based technique described above. This two-step procedure (QTL selection followed by re-estimation of their genetic effects) can be iterated until no locus is selected.

We evaluated the performance of the re-estimation procedure using 50 replicated data sets basing the QTL detection step on the SASP approach, using a single data replicate. The phenotype generation process was based on the same parameter setting as in Simulation study-II. Because we assumed that three consecutive loci represent the same QTL, only the locus with the largest effect size was preliminarily selected from each group of three consecutive loci for use in re-estimation in cases where the QTL effects were broken up to show significant effects over multiple loci. Our procedure was able to select the four loci corresponding to actual QTLs indices, namely loci 4, 25, 50 and 65, although this may not always be the case in practice. Moreover, no additional QTL was found in subsequent chromosome sweeps. This implies that the four loci selected for re-estimation seemed to fully account for the genetic signal in the data. We thus fitted the relaxed model restricted to these four loci to 50 replicated data sets. Figure 3 depicts the error bars (mean±s.e.) of the re-estimated posterior mean QTL effects over the 50 replicates.

Figure 3
figure 3

Error-bars (mean±s.e.) of re-estimated posterior mean QTL effects over 50 replicated data sets under the simulated dense marker map. The black solid circles represent the averaged posterior means over the 50 replicates and the grey diamonds represent the true values. QTL, quantitative trait locus.

Full size image

The results plotted in Figure 3 show that the re-estimation method can provide remarkably accurate estimates of the genetic effects. The estimated QTL-heritabilities of QTL1, QTL2, QTL3 and QTL4 averaged over the 50 replicates were, respectively, 0.13, 0.14, 0.36 and 0.40, which are close to the true values.

Discussion

In this paper we introduced the SASP approach to sparse Bayesian regularization, focusing on QTL mapping in experimental crosses. The rationale of the SASP-based shrinkage approach is to assign to each marker effect a hierarchical prior involving at the lowest level a GG distribution. The shape parameter of the involved GG distributions is set as a free parameter to be estimated alongside the other model parameters to accommodate a continuum of distributional shapes that can be optimized from the data.

We conducted two simulation studies based on real-world barley (H. vulgare L.) markers and on a synthetic dense marker map simulated through the WinQTL Cartographer 2.5 programme to evaluate the performance of our new method, using the EBL (Mutshinda and Sillanpää, 2010) as benchmark for comparison.

Simulation results showed that the separation between true QTL effects and spurious effects can be made clearer using the SASP-based Bayesian regularization model, making it a promising approach for QTL mapping where good separation is the ultimate goal.

Simulation results also showed that, with highly correlated markers, some estimated QTL effect sizes may be well below their true values as a result of multi-collinearity. We discussed a re-estimation procedure intended to mitigate the shrinkage-induced bias on the effects of detected QTLs. The methodology consisted of re-estimating the effects of detected QTLs without shrinkage (that is, under diffuse Gaussian priors) from the regression model barring the presumably spurious predictors. The search for additional QTLs may be attempted by pre-conditioning on the effects of the already selected loci until no QTL is detected. In simulations, the re-estimation procedure proved to provide remarkably accurate estimates of QTL effects. This approach may open new prospects for many disciplines such as bioinformatics where oversaturated models are booming.

It is worth mentioning that the re-estimation procedure consisting of separately solving subset selection and parameter estimation has already been considered in different settings. For example, Meinshausen (2007) proposed a relaxation to the LASSO penalty subsequently to initial model selection to address the issue of high bias of LASSO estimates in high-dimensional models. Our re-estimation approach is related to the (non-Bayesian) relaxed LASSO of Meinshausen (2007) when φ → 0. The LARS-OLS approach of Efron et al. (2004) is also based on the same principle.

The model fitting to the data was performed using MCMC methods using the freeware OpenBUGS. BUGS (WinBUGS or OpenBUGS) can be used to fit models of essentially arbitrary complexity without requiring the derivation of posterior distributions. It has, however, been pointed out (for example, Gelman and Hill, 2007, p. 567) that under BUGS, the MCMC samplers can be slow to converge in extremely high-dimensional or in the presence of highly correlated parameters. In such cases and instances where BUGS does not seem to work, one needs to write her/his own sampler and implement it in a convenient programming language. This may not be straightforward in many cases, including for the SASP-based shrinkage model proposed here. Supplementary Appendix E provides some guidelines as to how this can be done for our model, noting that a hybrid algorithm combining Gibbs sampling (Geman and Geman, 1984; Gelman et al., 2003) with Metropolis–Hastings ( Metropolis et al., 1953; Hastings, 1970) steps would be required. The Metropolis–Hastings steps are needed to sample from the posteriors of model parameters for which the full conditionals are not available in closed-form as is the case for the genetic effects bj, (j=1, …, p). A key advantage of user-designed samplers is that the analyst has direct control on the adaptive rules, and may, for example, select optimal proposal kernels for the Metropolis–Hastings steps.

It should be emphasized that the methodology presented here focuses on experimental crosses. With outbred populations, one needs to correct for confounding effects of population structure and cryptic relatedness (Sillanpää, 2011). However, simultaneous variable selection and estimation has been pointed out to be relatively robust to these confounders in multi-locus models (Pikkuhookana and Sillanpää, 2009; Sillanpää, 2011).

Many studies, including those by Edwards et al. (1987), Bost et al. (2001), Hayes and Goddard (2001) and Xu (2003b), have pointed out the typical L-shaped aspect of the distribution of (absolute) QTL effects. This feature follows from the fact that most of the marker effects are 0 or nearly so (that is, most of the mass of the QTL effects is concentrated near 0), with just a few ones having moderate-to-large effects. The tenet of the SASP-based approach introduced here is to infer the tail-decay rate of priors that are intended to induce the L-shaped distribution of estimated QTL effects, which is rather an outcome than a distributional model assumption.