Abstract
When drinking a cup of coffee under the morning sunshine, you may notice white membranes of steam floating on the surface of the hot water. They stay notably close to the surface and appear to almost stick to it. Although the membranes whiffle because of the air flow of rising steam, peculiarly fast splitting events occasionally occur. They resemble cracking to open slits approximately 1 mm wide in the membranes and leave curious patterns. We studied this phenomenon using a microscope with a high-speed video camera and found intriguing details: i) the white membranes consist of fairly monodispersed small droplets of the order of 10 μm; ii) they levitate above the water surface by 10 ~ 100 μm; iii) the splitting events are a collective disappearance of the droplets, which propagates as a wave front of the surface wave with a speed of 1 ~ 2 m/s; and iv) these events are triggered by a surface disturbance, which results from the disappearance of a single droplet.
Similar content being viewed by others
Introduction
As a Japanese physicist Torahiko Terada wrote in his fascinating essay “Chawan no yu (A cup of hot tea)” in 1922 (in “The Complete Works of Terada Torahiko”, vol 2, pp.3–9, Iwanami, 1997), many interesting phenomena occur in a teacup filled with hot tea, including convection, condensation and vortex flow. Many are related to a wide range of natural phenomena in larger scales and have been subjects of active study in physics during the last few decades. One phenomenon in his essay that has not been systematically studied is the misty thin skin that covers a hot water surface (Fig. 1). He also mentioned the crack patterns that run through the skins and conjectured that the patterns must be related to the temperature variation developed by the convection flow in hot water. Nearly 50 years later, another essay on this phenomenon was written by Schaefer in 19711. He performed some simple experiments and conjectured that the white skins were made of small charged droplets that levitated because of the rising evaporation flow from the surface. He contended that the patterns on the skins delineate the Rayleigh-Bénard convection pattern in hot water and suggested that the slits suddenly appeared because of micro whirlwinds that develop in the rising hot moist air flow.
Misty skins over hot coffee.
Peculiar patterns are observed in white membranes on the coffee surface. The photo is provided through the courtesy of Machida-Sagamihara portal site Vita (http://vita.tc) and Tamagawa Coffee Club and is allowed for use in this paper with reference to the companies.
Recently, a similar phenomenon was accidentally discovered by Fedorets in a different setting when he was examining the surface of water layer on an ebonite substrate heated with a lamp2. He found a layer of microdroplets of approximately 10 μm forming a triangular lattice and observed that a segment of a droplet cluster suddenly disappears within 0.04 sec, i.e., a single-frame interval of his video camera. In a series of works2,3,4,5, Fedorets and co-workers examined several conceivable mechanisms of the droplet levitation and suggested two possibilities: the force from droplet spinning because of the Marangoni effect and the Stokes drag force because of the rising evaporation flow.
In this work, we examine the surface of bulk hot water using a microscope with a high-speed video camera and report what the white membranes are and how the “cracking events” actually occur.
Results
We performed two sets of experiments: preliminary observations on several types of hot water/beverages and detailed observations on hot tap water with a high-speed video camera. The preliminary experiments were performed with a simple setting; the hot water/beverage in a beaker was examined by eye and with a video camera. We made observations on several types of hot water, such as coffee, tea, water with detergent and pure water filtered using a Milli-Q system and we did not find significant differences in the white membranes for all cases. The microscope observations showed that the white membranes consist of micro droplets of the order of 10 μm. The droplets were also found on the surface of moderately hot water with a temperature of approximately 50°C, although they were notably sparse.
After the preliminary observations, we made closer observations of hot tap water with a high-speed video camera using a setup designed for this phenomenon (Fig. 2). The experimental setup had a water container, a liquid light-guide illumination system and a microscope with a high speed-video camera (KEYENCE VW-9000, Japan). To avoid water condensation on the lens, the water surface was observed from below under bright- or dark-field illuminations from above. The dual wall chamber was used for the water container to reduce external disturbances. The container was filled with hot water of 60 ~ 90°C in the room temperature environment of 20 ~ 25°C; the room temperature and humidity were not controlled during the experiments. The recorded images were analysed using image-processing software, mainly ImageJ.
Snapshots
Figure 3 shows typical microscope pictures at three different temperatures. Droplets are scattered on the surface and drifting together at approximately a few mm/s. They do not stay on the surface but levitate above the surface, which is confirmed with the independence of their drift motions on those of dust particles that float on the surface. The distance above the surface is estimated to be 10 ~ 100 μm from the focus depth of the microscope.
Figure 3 shows the following: that the droplets are more populous and larger at higher temperature; that the droplets are relatively monodispersed at each temperature; that there is a clear boundary between the dense and the sparse regions of the droplets; and that the droplets tend to form a triangular lattice in the dense regions.
Figure 4 shows the size distributions and average sizes of the droplets at several temperatures. The radius distributions show narrow dispersion, whose standard deviations are typically less than half of their average value. The average radius of the droplet gradually decreases when the temperature decreases. The data at T < 60°C may contain systematic error because the average radius becomes comparable to the resolution limit of the images, i.e., 4.74 μm for 1 pixel.
Observations with high-speed camera.
Careful examination of the video images reveals that the droplets occasionally fall from above to settle above the surface and they occasionally fall down to the water surface to individually disappear. In addition to such individual disappearances, we observed occasional collective disappearances of hundreds of droplets within a single-frame interval of the 30 fps video camera; this collective event corresponds to the aforementioned splitting event. To study this fast process during the collective disappearance, we made observations using the high-speed video camera with frame speeds of 1000 and 8000 fps and a shutter speed of 1/16000 sec.
Figure 5 shows three consecutive frames of 1000 fps video, which captured a collective vanishing event. A millimetre-sized droplet cluster vanished within a couple of frame intervals. The streaks appeared in the middle frame because of the droplet motion during a single-frame exposure. It should be noted that not all droplets in the region vanished and there were surviving droplets, i.e., some isolated droplets and/or clusters of droplets survived in the region that had a collective event. The videos also show a continuous falling of droplets from above onto the surface, some of which settled in the clusters and caused rearrangement of the surrounding droplets (Supplementary video 1).
Collective vanishing event of a droplet cluster.
Three consecutive frames of the 1000 fps video are shown. Levitating water droplets are observed as the bright spots under dark-field illumination. (Supplementary video 2)
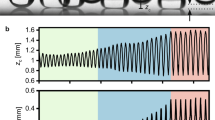
Figure 6 shows nine consecutive frames of the 8000 fps video, which reveal that the vanishing event propagated as a wave front at speed of approximately 1 m/s. It is also observed that the wave front was accompanied by a surface wave of the water, which propagated at an approximately identical speed. The four consecutive frames in Fig. 7 capture the initial stage of a collective event. The collective event was triggered by the disappearance of a single droplet, from which the disturbance wave front propagated outward and caused a massive disappearance event that involved thousands of droplets. We also observed concurrent events, where two collective and/or individual events occurred within a 10 ms time interval, although they did not seem causally related through the surface wave because they were spatially separated from each other.
Wave front propagation of a collective vanishing event.
Nine consecutive video frames of 8000 fps are shown. (Supplementary video 3)
Finally, Fig. 8 shows a vanishing event in the system with the surfactant Triton X-100. The concentration was 0.3 mM, which is above the critical micelle concentration at room temperature, i.e., 0.24 mM. One can observe that the event is qualitatively similar to the one in the tap water. The surfactant does not appear to significantly change the droplet size and the propagation speed.
Discussion
With these observations, we found the following: 1) The phenomenon is not sensitive to the type of water, i.e., coffee, tea, water with detergent and Milli-Q water; 2) the white membranes consist of the fairly monodispersed microdroplets that fall from above and levitate immediately above the water surface; 3) the typical size of the droplets is on the order of 10 μm, the average size decreases as the water temperature decreases and the levitation height is 10 ~ 100 μm; 4) the splitting events in the membranes are the propagation of the collective disappearance of droplets, which is triggered by a single droplet; and 5) their propagation fronts are accompanied by the surface wave, both of which propagate at ca. 1 m/s.
These observations provide more questions than answers: 1) What is the levitation force? 2) Why are the droplets so monodispersed? 3) What triggers the collective vanishing event? 4) How does the vanishing wave front propagate? 5) Why do some droplets survive after a vanishing event?
Non-coalescent drops
Before discussing some of these issues, let us briefly mention an apparently similar phenomenon, i.e., non-coalescent drops, which you may observe when you make drip coffee. Some drops stay on the coffee surface for several seconds and roll over it before they coalesce into the coffee in the pot. The droplets float above the surface also in this case, but the droplet size is notably different: 1 cm for the dripping droplets and 10 μm for the droplets in the white membranes. This type of non-coalescent liquid drops has been studied in various situations6,7 and it has been shown that two surfaces of the same liquid that are pressed against each other can be stabilised without coalescing for quite a long time because of a thin air layer, which is maintained by various mechanisms, such as the air drag by liquid viscosity8, externally driven air flow9, air flow driven by the thermal Marangoni effect10,11,12,13, surfactant surface elasticity14, or vibration8, etc. However, the relevance to the present phenomenon is not direct because of the size difference.
Levitation force
The required force to levitate a 10 μm diameter droplet against gravitation is approximately 5 pN. The levitation force may depend on the water temperature because the average droplet size increases with the water temperature. The evaporation flow from the hot water surface is a candidate as Schaefer previously conjectured in his essay1. Recently, this mechanism was examined in more detail by Fedorets and co-workers3,5. They also explored another mechanism; the droplets may be levitated by the air flow induced by the spinning motion because of the Marangoni effect3. They estimated that the droplets could spin as fast as 50 rotations per second (rps) by a possible temperature variation in the droplets. Both mechanisms should be sensitive to the water temperature and environmental humidity. Another possibility is an electrostatic force because small droplets can be easily charged. In the present case, the droplets are likely charged because they form a triangular lattice in densely populated regions. With this mechanism, the levitation force should be sensitive to the electric status of the surface, which should be affected by salt or other impurities in the water. It is puzzling that the phenomenon appears insensitive to variations in the water temperature, humidity and water purity.
Size distribution of the droplets
The droplets are relatively monodispersed. The standard deviations of the linear size distributions are less than 50% of the averages. If there is no particular size of approximately 10 μm for the droplets to be thermodynamically stable, their size may be selected based on the force balance between gravitation and the levitation force.
In a slightly different situation from the present case, Arinshtein and Fedorets made an interesting observation on this connection4: there appeared droplets as large as 100 μm in diameter over the water layer on the ebonite substrate when the water surface was heated at a localized region of 1 mm in size.
Vanishing events
Droplets individually and collectively vanish. In a collective event, the vanishing front propagates at approximately 1 m/s, which is close to the capillary surface wave speed of the water with a wave-length of 0.1 ~ 1 mm. Thus, it is natural to assume that the droplets are swamped by the surface wave, which is sustained by the surface energy of the swamped droplets. A simple estimate of the energy balance shows that the energy input from the swamped droplets can maintain the surface wave with a sufficiently large amplitude to swamp the droplets in the regions of high density of droplets (see the Methods section).
We observed that a single-droplet disappearance caused a collective event, although there are also many isolated events that do not trigger a collective event. The single-droplet events tend to occur in less populous regions, which is consistent with the above mechanism of collective vanishing because in a sparse region, the disturbance decays before it reaches neighbouring droplets; otherwise, it should trigger a collective vanishing event.
Whether a vanishing event triggers a collective event or not, it is not clear what causes a droplet to vanish in the first place; the reason may be fluctuations in the evaporation flow or an electric disturbance that is caused by a cosmic ray if the droplets are levitated by the electrostatic force. The observed concurrent events are likely to be triggered by a common disturbance in the levitation force because it is highly improbable that more than one event occurs in less than 10 ms in a small area of the microscope field of view.
If the levitation force is provided by the temperature, the spatial pattern of the droplet disappearance events may reflect spatial variations in the surface temperature of the water, which would explain the observation of Terada and Schaefer1 that the splits in the white membranes appear to delineate the Rayleigh-Bénard convection pattern in the cup. The collective disappearance events should in the low-surface-temperature region of descending convection, where the levitation force is weaker and thus the droplets stay closer to the surface.
Surviving droplets
If the swamp mechanism of the collective droplet disappearance is true, some droplets can survive if they are levitated higher. However, the surviving droplets do not necessarily appear smaller than the vanished droplets, which does not appear consistent with the idea that the levitation height is determined by the force balance because a smaller droplet should stay higher in this mechanism. To determine the mechanism, experimental observations of the levitation heights and their correlation with the droplet size and surface temperature are important.
In conclusion, a cup of hot tea continues to provide us with interesting phenomena that deserve scientific research. The phenomenon that we studied here can be observed everyday and should have been noticed by many scientists, yet very few people appear to have imagined such fascinating phenomena happening in a teacup.
Methods
In this section, the amplitude of the surface wave is estimated based on the described swamping mechanism. In the steady propagation, there should be an energy balance between the energy input from the swamped droplets and the energy dissipation in the surface wave because of the viscosity. Assuming that the surface wave is localised around the wave front region with the width and depth of the wave-length λ (Fig. 9), the energy dissipation per unit time per unit length along the wave front is estimated as

where η is the water viscosity, τ is the wave period and h is the height or amplitude of the wave. The energy input is estimated as the product of the number of swamped droplets and the surface energy of a droplet,

where v ≡ λ/τ, n, σ and d are the wave speed, area density of the droplets, surface tension of the water and droplet diameter, respectively. By equating ediss and einput, we obtain

If we use

with the following viscosity and the surface tension for water,

Eq. (3) is estimated as

This estimate suggests that the sufficiently large amplitude of the surface wave can be maintained by the surface energy of the swamped droplets for the observed droplet density in densely populated regions.
Change history
15 July 2015
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.
References
Schaefer, V. J. Observations of an early morning cup of coffee. Am. Sci. 59, 534–535 (1971).
Fedorets, A. Droplet cluster. JETP Lett. 79, 372–374 (2004).
Fedorets, A. On the mechanism of noncoalescence in a droplet cluster. JETP Lett. 81, 437–441 (2005).
Arinshtein, E. & Fedorets, A. Mechanism of energy dissipation in a droplet cluster. JETP Lett. 92, 658–661 (2010).
Fedorets, A., Marchuk, I. & Kabov, O. Role of vapor flow in the mechanism of levitation of a droplet-cluster dissipative structure. Tech. Phys. Lett. 37, 116–118 (2011).
Rayleigh, L. Investigations in Capillarity:–The size of drops.–The liberation of gas from supersaturated solutions.–Colliding jets.–The tension of contaminated water-surfaces. Phil. Mag. 48, 321–337 (1899).
Neitzel, G. P. & Dell'Aversana, P. Noncoalescence and nonwetting behavior of liquids. Annu. Rev. Fluid Mech. 34, 267–289 (2002).
Couder, Y., Fort, E., Gautier, C.-H. & Boudaoud, A. From bouncing to floating: Noncoalescence of drops on a fluid bath. Phys. Rev. Lett. 94, 177801 (2005).
Sreenivas, K. R., De, P. K. & Arakeri, J. H. Levitation of a drop over a film flow. J. Fluid Mech. 380, 297–307 (1999).
Dell'Aversana, P., Banavar, J. R. & Koplik, J. Suppression of coalescence by shear and temperature gradients. Phys. Fluids 8, 15–28 (1996).
Dell'Aversana, V., Tontodonato, P. & Carotenuto, L. Suppression of coalescence and of wetting: The shape of the interstitial film. Phys. Fluids 9, 2475–2485 (1997).
Monti, R., Savino, R. & Tempesta, S. Wetting prevention by thermal marangoni effect. experimental and numerical simulation. Euro. J. Mech. B 17, 51–77 (1998).
Savino, R., Paterna, D. & Lappa, M. Marangoni flotation of liquid droplets. J. Fluid Mech. 479, 307–326 (2003).
Amarouchene, Y., Cristobal, G. & Kellay, H. Noncoalescing drops. Phys. Rev. Lett. 87, 206104 (2001).
Acknowledgements
The authors thank Clive Ellegaards, Namiko Mitarai, Takahiro Sakaue and Yoko Ishii for stimulating discussions. This work was supported by JSPS KAKENHI Grant Number 25610124.
Author information
Authors and Affiliations
Contributions
H.N. and M.I. wrote the main manuscript text and T.U., M.O. and M.I. performed the experiments. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Umeki, T., Ohata, M., Nakanishi, H. et al. Dynamics of microdroplets over the surface of hot water. Sci Rep 5, 8046 (2015). https://doi.org/10.1038/srep08046
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep08046
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.