Introduction

Versatile, low-power means to selectively control magnetization states at the nanoscale are critical across a host of applications, both in fundamental science and device-oriented systems. Alongside mature technologies such as data storage, nanomagnetic arrays support a host of more recent applications including neuromorphic computation1,2,3,4,5, superconducting vortex control6,7,8,9 and reconfigurable magnonic crystals10,11,12,13,14 (RMCs). RMCs are nanopatterned metamaterials harnessing varying magnetic configurations to manipulate and store information by tuning magnonic (spin-wave) dynamics15,16,17,18,19,20,21,22,23,24,25,26.

RMCs promise to be key functional elements in the burgeoning field of magnonics13,16,17,18,19,21,22. Comprising arrays of interacting nanomagnets, different magnetization configurations of the array (or ‘microstates’) allow a range of functional behaviours including amplifying and attenuating specific frequency channels27,28,29,30,31 or bandgap creation and tuning32,33,34. Existing magnonic crystal designs have shown strong initial promise, but are severely limited by a lack of practical means to access more than a handful of microstates. N-element arrays possess 2N microstates and, typically, systems with 210–2100 potential microstates are restricted to operating within just two or three configurations11, imposing a hard limit on scope and utility.

Of the existing microstate control techniques, from simple applications of system-wide magnetic fields to Oersted-field stripline techniques and intricate multilayered spin-transfer torque devices35,36,37,38, few are able to selectively reverse the magnetization of an arbitrary element in a strongly interacting nanoarray without affecting neighbouring elements. Many approaches struggle to function without disturbing delicate magnetic states elsewhere in the system due to large stray fields or a reliance on global external fields. The remaining methods rely on mechanical apparatus orders of magnitude larger than the nanomagnet, either a hard-disk style write-head or scanning-probe with magnetic tip39,40,41—unsuitable for on-chip integration and susceptible to damage.

To address the pressing need for non-invasive, global-field free means for nanomagnetic writing, we build on the fundamental principles of ‘topological magnetic writing’39 to present a scheme enabling low-power, fully solid-state access to the entire microstate space of strongly interacting nanomagnetic systems. The tightly localized stray field of a current-driven 180° transverse domain wall (DW) in a nanowire is used to induce dynamic topological defects in adjacent ferromagnetic (FM) nanoislands, driving magnetic reversal. Topological defects in planar nanomagnets are conserved quasi-particles protected by energies on the order of the exchange interaction, granting the writing method strong thermal stability and tolerance for patterning imperfections42,43,44. By varying the drive-current amplitude in the nanowire, fully selective reversal is achieved and nanoislands may be switched or ‘skipped’ at will as the DW passes. The versatility and utility of the technique are demonstrated via two active magnonic system designs: a reconfigurably gateable one-dimensional (1D) transmission-line RMC optimized for travelling-wave magnons supporting multiple gate types and on/off ratios up to 35 and a two-dimensional (2D) RMC optimized for standing-wave magnons with single-frequency on/off ratios of up to 9 × 103 and mode shifting of Δf = 0.96 GHz.

Results and discussion

Working principle of reversal method

The reversal process is depicted schematically in Fig. 1a–d with a corresponding time evolution series shown in Fig. 1e. The system comprises a FM DW-carrying ‘control’ nanowire (here Permalloy (Py)) and Ising-like Py ‘bit’ nanoisland(s) at a height h below the control wire. The control wire serves as a track allowing a transverse control-DW (hereafter c-DW) to traverse the nanoislands via current-induced spin-transfer torque. The c-DW stray field influences the nanoisland magnetizations as it moves over them, allowing the islands to serve as rewritable bits. N.B. the c-DW nomenclature serves just to distinguish the control-nanowire DW from DWs in the bit nanoislands. All DWs discussed are standard transverse DWs. Figure 1e shows a detailed micromagnetic time evolution of the reversal process. Here we view a single Py nanoisland from above (positive z-direction, nanoisland in the xy-plane) as traversed by a c-DW (white circle) in the Py control nanowire, moving with \({v}_{{\rm{c}}-{\rm{DW}}}=+\hat{x}\). The nanoisland is initially magnetized with \(M=-\hat{y}\) and the chirality of the c-DW such that its magnetization at the c-DW centre points in the \(-\hat{z}\) direction towards the nanoisland. The nanoisland dimensions are 400 × 75 × 5 nm3 and the nanowire has quasi-infinite length, 40 × 40 nm2 cross-section and suspension height h = 10 nm above the nanoisland.

Fig. 1: Schematic of the magnetic reversal method.
figure 1

a Representation of the ferromagnetic domain wall-carrying ‘control’ nanowire and ‘bit’ nanoisland, separated by a non-magnetic gap of height h. b–d Time-evolution series of the magnetic reversal process in two-nanoisland system. Both nanoislands are initially magnetized with \(M=-\hat{y}\) (b) before the current-driven ‘control’ domain wall (c-DW) traverses the right-hand nanoisland, inducing magnetization reversal (c), leaving it magnetized \(M=+\hat{y}\), whereas the left-hand nanoisland remains unswitched (d). It is noteworthy that the internal domain wall structure in c and d is slightly distorted by the drive-current; b shows the static, relaxed domain wall state. e Detailed time-evolution series of the reversal process in a single 400 × 75 × 5 nm3 nanoisland. The dynamic c-DW is represented by the white circle traversing the nanoisland midpoint, moving with \({v}_{{\rm{c}}-{\rm{DW}}}=+\hat{x}\). t = 0 s is defined when the c-DW begins moving from its origin, 112 nm to the nanoisland’s left. The partially formed contorted nanoisland domain wall is highlighted in t = 0.6 ns by the dashed grey line, with the partially formed straight island domain wall highlighted by longer grey dashes in t = 0.65 ns. Topological defects are labelled with their winding numbers. Corresponding time-evolution series are provided in Supplementary Movies 1–6.

Full size image

As the c-DW approaches the nanoisland (Fig. 1e, t = 0.6 ns), the c-DW stray-field HDW distorts the spins on the left edge of the nanoisland, forcing them out of a collinear state to lie along the locally divergent radial HDW. This distortion of the nanoisland magnetization introduces a pair of edge-bound topological defects with opposite polarity  ±1/2 winding numbers43, seen on the nanoisland left edge. Winding numbers in a ferromagnet are conserved and must sum to 1 in a hole-free nanoisland. As the c-DW progresses across the nanoisland (t = 0.65 ns), the influence of HDW extends to the nanoisland’s right edge, eventually causing a corresponding pair of edge-bound ∓1/2 topological defects to form (t = 0.7 ns).

Continuous chains of reversed spins now connect each topological defect pair across the nanoisland width, effectively binding the  ±1/2 defects together via the exchange-energy penalty for breaking the spin chains. Each bound defect pair constitutes a 180° DW; however, the two nanoisland DWs (hereafter i-DWs) are formed asymmetrically. The lower (y-direction) i-DW directly under the c-DW path (dashed white arrow in panel t = 0.6 ns) forms in its lowest-energy straight conformation parallel to the nanoisland width, as HDW is locally oriented along this axis. For the upper i-DW, HDW is oriented in the positive y-direction antiparallel to the initial nanoisland magnetization. This forces the nascent upper i-DW to assume a contorted conformation around the growing \(M=+\hat{y}\) domain (yellow–green region in Fig. 1e), with a corresponding exchange-energy penalty relative to the straight lower i-DW. The difference in nascent i-DW conformations is seen in t = 0.65 ns, with the lower, straight and upper, contorted i-DWs highlighted by long and short grey dashed lines, respectively.

Once the c-DW progresses far enough to introduce topological edge defects to the nanoisland’s far side, the \(M=+\hat{y}\) domain is fully formed and the contorted i-DW no longer forced to assume a high-energy conformation. As such it rapidly straightens out, assuming a low-energy conformation straight across the nanoisland width and converting its excess exchange energy into motion in the process. The released exchange energy propels the i-DW along the nanoisland in the positive y-direction until it collides with the nanoisland’s upper end. Upon reaching the island end the  ±1/2 defects are free to reach and annihilate each other, unwinding the i-DW to a collinear state and emitting a spin-wave burst down the nanoisland (t = 0.9 ns). The spin-wave burst interacts with the remaining i-DW39,41,45, exerting a torque that accelerates it towards the nanoisland bottom (t = 1.3 ns). As the remaining i-DW approaches the nanoisland bottom, it is increasingly magnetostatically attracted to it, further driving acceleration (t = 2.0 ns) until the i-DW unwinds on contact as described above, leaving a DW-free nanoisland magnetized antiparallel to its initial state (t = 2.5 ns) with reversal completed  ~2 ns after the c-DW reaches the nanoisland.

Distinct modes of reversal method

The process above describes the core physics behind the reversal process, however the Oersted-field HOe arising from the drive-current through the control nanowire has not yet been considered. In the absence of HOe (for instance, if the c-DW was driven via global B field), the reversal process occurs as described previously for all permutations of Ising-like initial nanoisland magnetizations (\(M=\pm\hat{y}\)) and c-DW trajectories (\({v}_{{\rm{c}}-{\rm{DW}}}=\pm\hat{x}\)). However, reversing the c-DW velocity when driving via current requires reversing the current direction and therefore the direction of HOe in the nanoisland plane (±y-direction). This leads to two distinct reversal regimes occurring at different nanowire suspension heights: a fully selective mode where h = 20–5 nm, allowing reversal of any desired element in a nanoarray, and a close-proximity mode allowing nanoisland reversal at lower current density and higher bit-density than HOe stripline-based techniques occurs where h = 2–11 nm, albeit at reduced selectivity relative to the h = 20–25 nm mode. Nanoislands of dimensions 400 × 75 × 5 nm3 are considered in both reversal regimes.

Close-proximity, low-power reversal mode

Considering first the close-proximity mode, here the contorted high-energy i-DW is injected with sufficient energy to overcome the influence of both possible \(\pm \hat{y}\)HOe directions and will unwind into its nearest nanoisland end as the c-DW passes as in Fig. 1e, t = 0.7–0.9 ns. However, the behaviour of the initially static low-energy i-DW is determined by the drive-current polarity and corresponding HOe direction. Figure 2 shows the low-energy i-DW driven ‘favourably’ (a) by an HOe aligned antiparallel to the initial nanoisland magnetization—unwinding at the opposite nanoisland end as the high-energy i-DW and successfully mediating reversal, or ‘unfavourably’ (b) by an HOe parallel with the initial island magnetization—unwinding at the same end as the high-energy i-DW, leaving an unswitched nanoisland magnetized along its initial direction. The dependence of reversal success on initial nanoisland magnetization is illustrated in Fig. 2c, where a four-nanoisland array is prepared in a mix of ‘favourable’ (islands 1 and 4) and ‘unfavourable’ initial magnetization states. After c-DW traversal, only the favourably magnetized islands are reversed.

Fig. 2: Close-proximity and fully selective reversal modes.
figure 2

a–c Close-proximity reversal mode. d Fully selective reversal. a With Oersted-field HOe antiparallel to the initial nanoisland magnetization HOe aids reversal, driving the low- and high-energy nanoisland domain walls (i-DWs) to opposite nanoisland ends and achieving successful switching. b With HOe aligned to the initial nanoisland magnetization, the reversal process is hindered, HOe drives the low- and high-energy i-DWs into the same nanoisland end, resulting in failed switching. c Four-island array initialized (‘before’ panel) with second and third islands in \(M=+\hat{y}\) state, and first and fourth in \(M=-\hat{y}\) state. Control domain wall (c-DW) is then driven across the array such that \({{\bf{H}}}_{{\rm{Oe}}}=+\hat{y}\), driving successful reversal of \(M=-\hat{y}\) islands (as described in a) and failed reversal of \(M=+\hat{y}\) islands (as in b). d c-DW begins to the left of two nanoislands (t = 0). It is driven over the first nanoisland by a J = 2.0 × 1012 A/m2 ‘skip’ current pulse, leaving the nanoisland unswitched as HOe + HDW < HN, the nucleation field. The c-DW is then driven over the second nanoisland with a J = 5.5 × 1012 A/m2 ‘write’ pulse, switching the nanoisland magnetization as HOe + HDW ≥ HN.

Full size image

Successful reversal therefore requires an HOe aligned antiparallel to the initial nanoisland magnetization. This means that in the close-proximity regime microstates may be written from a collinear initial state (all nanoislands identically magnetized) such that every nanoisland traversed by the c-DW is switched, with the halting point of the c-DW decided by the user. For instance, in a field-saturated ten-island array with c-DW initialized left of the array, island 1 could be switched, or islands 1–5, but island 5 could not be switched without reversing islands 1–4. For the 400 × 75 × 5 nm3 nanoislands considered here the close-proximity mode functions with a minimum current density of J = 3 × 1012 A/m2 for 5 nm-thick Py nanoislands, a factor of 2.3×  lower than the minimum J required for conventional non-selective HOe reversal of matching nanoisland and nanowire dimensions. As power consumption and Joule heating scale as J2, c-DW-driven reversal leads to an 82% reduction in power consumption compared to using only the Oersted field while still affording partial selectivity.

The upper bound of h = 11 nm is given for close-proximity reversal as for lower separations, the minimum J required to overcome magnetostatic attraction between c-DW and nanoisland and move the c-DW across the island will also generate sufficient HOe to switch the nanoisland, negating ‘skip’ events where the c-DW passes a nanoisland without switching it and hence preventing full selectivity. Increments of 0.5 nm were considered for h down to a minimum of h = 2 nm.

Fully selective reversal mode

In the fully selective h = 20–25 nm regime, the increased nanowire–nanoisland separation means the magnitude of the c-DW stray field HDW at the nanoisland is lower than the critical nucleation field HN required to overcome exchange energy and begin locally rearranging spins to nucleate a nascent domain; hence, HDW alone is unable to drive reversal. However, when combined with a sufficient magnitude HOe such that HDW + HOe ≥ HN, reversal occurs as described above. This allows for two current-driving operations to be performed as shown in Fig. 2d: a ‘skip’ event (t = 1.7 ns), where a low current-density pulse J = 1.5–3.0 × 1012 A/m2 is used to move the c-DW over a nanoisland, while maintaining an HOe magnitude below the reversal threshold, and a ‘write’ event (t = 2.9 ns) where a higher current-density pulse J = 5.0–7.0 × 1012 A/m2 is used to move the c-DW, while providing a sufficiently high HOe such that magnetic reversal occurs (Fig. 2d), t = 1.4 ns). By combining sequences of these ‘skip’ and ‘write’ events, any desired microstate may be realized. To allow for reliable position-control of the c-DW, 5 nm notches were inserted into the control nanowire between island positions (seen in Fig. 2d), providing local potential wells to ensure that c-DW traverses only one island per pulse and provide a well-defined end position for the c-DW after each pulse.

The threshold current values were determined using simulation increments of 0.5 × 1012 A/m2 and defined as follows; ‘skip’ mode: above minimum J to overcome magnetostatic attraction between c-DW and nanoisland and drive the c-DW across the nanoisland, and below maximum J satisfying HDW + HOe < HN—and ‘write’ mode: above minimum J satisfying HDW + HOe ≥ HN and below maximum J where induced nanoisland DWs leave a non-turbulent regime and begin exhibiting Walker breakdown, which can cause stochastic reversal failure by driving both i-DWs into the same nanoisland end. Functionality of both reversal modes in nanoisland arrays was investigated, with both modes acheiving switching as described above down to a minimum inter-island spacing of 60 nm, below which dipolar coupling between islands begins to interfere with the reversal process. The current densities employed here are on the high side, but similar to those employed in existing devices46. There is significant scope for reducing current density, with several relevant approaches investigated in the literature including material choice47, nanowire geometry48,49,50, or replacing the DW with another magnetic charge source such as a Skyrmion51.

Existing solid-state magnetic reversal schemes require two control lines to address a single element in an array; typically two orthogonal sets of current lines above and below the array35,36,37,38. Here, the same control is achieved with a single set of lines, a reduction of n lines in an n-row array. The c-DW may be prepared electrically using previously described stripline-based schemes44,52.

One-dimension RMC: reconfigurably gated waveguide

Magnonic device designs hinge on deterministic control of the magnon signal output, either via amplitude or phase modulation. Amplitude control has been demonstrated in two-state ‘transistor’-like devices and via a 1D gateable RMC11,13,21,23,53,54,55,56. However, gate positions are static—hard-coded at the nanofabrication stage by distinct patterning of ‘gate’ nanoislands relative to the rest of array and microstate control is restricted to just two of the 2N available states (in an N-island array) and reliant on global-field sequences. These designs function well and are important proofs of concept, but the reliance on global-field limits their utility in systems containing magnetically sensitive states and presents device integration challenges and static gate positions limit flexibility and scope. In addition, the number and location of distinctly patterned gate nanoislands affects the frequency and Q-factor of resonant modes even in the ungated state, causing functional behaviour to vary between arrays with different gate positions or numbers.

Here we present an RMC allowing reconfigurable current-controlled gating with no global-field requirement or differential nanoisland patterning. The design comprises a 1D nanoisland array situated above an underlying control nanowire. Selective nanoisland reversal is achieved by using current-pulses to shift the c-DW position relative to the array as described above. Our reversal scheme allows for a range of gate types, from single-island gating to more complex multi-island gates offering a range of functional benefits.

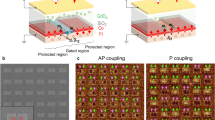
The RMC is depicted schematically in Fig. 3a, comprising 25 Py nanoislands of dimensions 350 × 120 × 5 nm3 with 60 nm inter-island spacing and 40 × 40 nm2 cross-section Py control nanowire along the array long axis. The first four islands are covered by a 550 nm wide Au coplanar waveguide, using pulsed HOe to locally excite magnons via which propagate along the RMC via dipolar inter-island interactions. The nanoislands have stable Ising-like magnetization in the  ± y-direction, initialized here with \(M=\hat{y}\) referred to as the ‘ungated’ state. Figure 3b–k illustrate magnon power transmission through the RMC in a selection of array microstates. Figure 3h shows the spatial power map of the magnon edge mode centred on 2.1 GHz in the ungated array, with good magnon transmission throughout the array. Considering first the fully selective reversal mode (control nanowire at h = 20 nm above nanoislands), Fig. 3b, e, i show the ‘single gate’ case, where one nanoisland in the array is reversed to \(M=-\hat{y}\) via a high-J ‘write’ c-DW traversal. Figure 3i shows magnon transmission strongly attenuated at the reversed gate island with ‘on/off’ ratios up to 10 observed (Fig. 3e), calculated from the ratio of integrated power at island 20 in the ungated to gated case.

Fig. 3: Schematic of the one-dimensional reconfigurable magnonic crystal.
figure 3

Coplanar Au microwave waveguide is at image top and underlying domain wall-carrying control nanowire is shown protruding at image bottom. b–d Edge-mode spin-wave power vs. array position for b single, c ‘antiferro’ and d ‘domain’ gate types. Coplanar microwave waveguide covers islands 1–4. Nanoisland positions denoted by dashed vertical lines with power vs. position traces colour-coded by gate position. e, f Corresponding magnon ‘on/off’ ratio vs. gate position for each gate type, calculated from the ratio of integrated power at island 20 in the ungated to gated case. h–k Spatial power maps of resonant magnon edge mode for h ungated, i single, j ‘antiferro’ and k ‘domain’ gate types. Power is normalized to ungated case. Array microstate is shown with green (purple) representing unswitched (switched) islands magnetized in the positive y (negative-y) direction. Control nanowire is shown over array, coplanar Au waveguide covers islands 1–4. Control nanowire is in fully selective h = 20 nm reversal regime for all cases other than ‘domain gate’, which operates in low-power h = 10 nm regime.

Full size image

One benefit of our reversal technique is the freedom to explore gating involving multiple reversed nanoislands. Figure 3c, f, j show one example of this, involving two reversed islands separated by an unreversed island. Termed an ‘antiferromagnetic’ (AFM)-type gate, on/off ratios are substantially improved to  ~30 across a range of gate positions with a peak ratio of 35 at position 5. While the previous gate types may be accessed in the fully selective h = 20 nm reversal mode, the low-power reversal mode switches all nanoislands traversed by the c-DW so microstates containing isolated reversed islands in otherwise unreversed arrays are not possible. With this in mind, Fig. 3d, g, k show a h = 10 nm RMC in a gated state comprising continuously reversed nanoislands one on array side with the other side left unreversed, termed a ‘domain’-type gate. The presence of the c-DW in the h = 10 mode introduces a 180° DW in the adjacent nanoisland from the influence of HDW, seen in the Fig. 3k microstate. This is the stable relaxed state and serves to improve gating efficacy relative to domain-type gates prepared in the h = 20 nm mode which do not introduce 180° DWs to any nanoisland. The ratios acheived here compare well with existing designs, matching or outperforming the prior art11,54,55,56 for a single-island gated 1D array RMC using differential patterning of the gate island. The domain-type gate perpared in the low-power, h = 10 nm reversal mode has the additional benefit of affecting the bulk-localized magnon mode more significantly than other gate cases, illustrated in Supplementary Fig. 1 with accompanying discussion in Supplementary Note 1.

Two-dimension RMC: reconfigurable filter

The 1D RMC above controls travelling k ≠ 0 magnon modes. Here we present a second RMC design leveraging the reversal method to control standing-wave k = 0 magnons in a 2D nanoisland array. Manipulating frequency and intensity of standing-wave magnons allows for key functionality including opening and closing specific frequency channels and selective band-pass filtering, with enhanced q-factor and transmission/rejection ratios relative to travelling-wave magnons27,28,29,30,31,32,33,34,57.

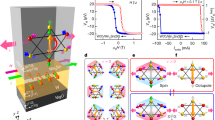
The RMC is depicted schematically in Fig. 4a, comprising adjacent columns of Py nanoislands each with a corresponding DW-carrying control nanowire. Columns are separated by a gap gx and islands within a column by gap gy. Adjacent columns are offset in the y-axis by a gap \(\frac{{g}_{y}}{2}\) to optimize dipolar coupling and hence difference between spectra of distinct microstates. The array considered here has nanoisland dimensions 300 × 94 × 5 nm3 and inter-island spacings gx = 84 nm, gy = 190 nm. Dimensions and spacings were optimized for RMC gain functionality.

Fig. 4: Two-dimension magnonic crystal.
figure 4

a Schematic of the 2D magnonic crystal incorporating control nanowires above each column of the nanomagnet array. b–d Schematics of the b FM, c AFM and d ‘stripe’ microstates illustrating magnetization directions of each nanoisland and control-nanowire positions. e Spin-wave spectra of ferromagnetic (FM), antiferromagnetic (AFM) and ‘stripe’ microstates on a 4 × 6 nanoisland magnonic crystal. Each state shows two main resonances, an edge-localized mode (1–3 GHz) and a centrally localized mode (5–8 GHz). Spatial magnon power maps for each mode are displayed next to peaks. f Spin-wave amplitude gain achieved by transitioning between microstates, i.e., moving from FM to AFM state (solid orange line).

Full size image

Figure 4b–d show three microstates termed ‘ferromagnetic’ (FM) (b), ‘antiferromagnetic’ (AFM) (c) and ‘stripe’ (d), accessible via shuttling c-DWs through control nanowires as described above. The RMC was prepared in each microstate and the spin-wave response studied after broadband excitation via an out-of-plane HExt sinc pulse. Figure 4e shows the resultant spin-wave spectra, with two distinct modes present for each microstate; a nanoisland-edge localized 1–3 GHz mode (fedge of 2.43, 1.78 and 2.74 GHz for FM, AFM and stripe, respectively), and a nanoisland-centre localized 5–8 GHz mode, with spatial mode profiles displayed next to each peak. The cause of distinct modes in each microstate is the differing local field Hloc profile from nanoisland stray dipolar fields58,59,60,61,62,63,64,65. These are at their strongest at the nanoisland edges and it follows that the edge-localized modes display greater microstate sensitivity. This sensitivity allows for considerable mode control, with a frequency shift of Δf = 0.96 GHz achieved by transitioning between the AFM and stripe states, with the FM state providing an interstitial frequency midpoint.

In addition to frequency shifting, microstate control affords substantial magnon amplitude modulation. Figure 4f shows the gain factor obtained by switching between the three microstates, with a gain of  ~9 × 103 achieved at the FM peak frequency f = 2.43 GHz by moving between the FM and AFM states, and a gain of  ~1 × 103 achieved at the AFM peak frequency f = 2.74 GHz by moving between the AFM and stripe states. The h = 20 nm fully selective mode is capable of accessing the entirety of the RMC’s microstate space, the three states presented here are a representative selection of the potential functionality available. States such as ‘AFM’ where entire columns of nanoislands are reversed are accessible in the h = 10 nm low-power mode, with the added benefit that control nanowires need only be patterned for the reversed columns—a reduction of 50% in the AFM case. In addition, array geometries containing nanoislands at different angles such as square artificial spin ice62,64 may be written by patterning control nanowires above and below the nanoislands at different angles. For instance, in the case of square artificial spin ice the y-axis control nanowires may be below the nanoislands and the x-axis control wires above.

The states in Fig. 4 are chosen as they have identical Hloc values at each nanoisland (relative to the nanoisland magnetization) so magnon modes are clearly defined. However, the writing technique enables access to all microstates, including states with different Hloc values at different array positions and hence multiple magnon modes. These mixed-Hloc microstates may be finely tailored, providing control over mode amplitude, frequency, bandwidth and the number of active modes. Detailed discussion of mixed states and their spectra is presented in Supplementary Fig. 2 and Supplementary Note 2 including the effects of gradual transitions between the FM, AFM and stripe states. Both RMC described here are suitable for signal readout via optical (micro-focused Brillouin light spectroscopy) or electrical (FM resonance) means.

Conclusions

In this work, we outline a powerful fully solid-state magnetic writing technique, allowing total microstate control without global fields and excellent integration propspects for on-chip systems. The technique allows a class of nanomagnetic systems deriving versatile functionality from a broad range of microstates to become viable candidates for technological advancement, as evidenced by the two RMC designs presented here.

By opening the entire range of microstates for exploration and exploitation, the writing technique described here invites a host of novel nanomagnetic system designs, in addition to the refinement and enhancement of existing designs which are currently limited to narrow regions of microstate space. Functional benefits are offered across diverse applications including neuromorphic logic and superconducting vortex control.

Although Py is employed as the FM material throughout this work, it is chosen for its ubiquity and familiarity in current nanomagnetic systems and near-zero shape anisotropy rather than ideal magnonic performance. Low-damping ferromagnets such as YIG66, various Heusler alloys67,68 and more simple bimetallic alloys such as CoFe69 have superior characteristics for low-loss, longer distance magnon transmission, enhancing functionality of the proposed and related devices incorporating our reversal method. In addition, the array dimensions reported here represent a proof-of-concept and are chosen to be readily fabricated using widely available equipment and techniques. Reducing array separation and fine tuning dimensions will enhance the spectral effects reported here and the related functionalities. We have focused here on magnetic reversal of Ising-like nanoelements. Prior studies have demonstrated injection of 360° DWs41 and Skyrmions using related locally divergent stray fields (magnetic force microscope tips in these cases) in nanostructures and writing states in nanodisks70. The DW-based writing method is highly suitable for integration with such writing schemes, offering substantial future scope.

Methods

Reversal method

All simulations were performed using MuMax3 71,72,73. Magnetic parameters for Py (Ni80Fe20) of A = 13 pJ/m, α =  0.02 and Ms = 800 × 103 kA/m. A cell size of 4 × 4 × 4 nm3 is used and two numerical solvers are employed at different stages of the simulation: (i) an equilibrium head-to-head transverse domain wall is formed in the nanowire by minimizing the total energy of the system using the conjugate gradient method and (ii) the temporal evolution of the system is computed by solving the modified version of Landau–Lifshitz–Gilbert equation that includes terms for spin-transfer-torque using the Dormand–Prince method (RK45)72. The advantage of the Dormand–Prince method is adaptive time steps, dependent on the error magnitude at each iteration, reducing computational intensity.

Boundary conditions are applied to the current-carrying nanowire ends to remove surface charges and associated stray fields, simulating a quasi-infinite wire. A 5 nm window of spins at wire ends are fixed to eliminate turbulent fluctuations when an electric current is applied. HOe in and around the current-carrying nanowire is simulated by solving Maxwell’s equation ∇ × B = μ0J, approximating the wire as an infinitely long cylinder and adding the corresponding vector field component to each of the finite-difference cells. The validity of the cylindrical-wire assumption was examined using Finite Element Method Magnetics74, with the comparison between HOe profiles of cylindrical and cuboid nanowires shown in Fig. 5. Near-identical field profiles are seen, with the small discrepancy for low distances from the nanowire accounted for in the reversal simulations by varying J to match the cuboid case.

Fig. 5: Field profiles of current-carrying cylindrical and cuboid nanowires.
figure 5

Field profile experienced by a nanoisland that is positioned h = 10 nm below an infinitely long cylinder and cuboid. There is a small discrepancy of 0.15 × 104 Am−1 around x = 0, which can be minimized by adjusting the value of the current density.

Full size image

Reconfigurably gated magnonic waveguide

To remove stochasticity from nanoisland edge-curl states (i.e., s-  and c-states) and allow direct comparison between gating types and positions, arrays are relaxed in a 1 mT global field, applied 5° above in the positive x-direction.

Magnons are excited with a 20 mT sinc pulse in the z-direction applied locally under the Au waveguide, exciting modes up to 20 GHz. The function has a sinusoidal wavelength of 550 nm along the array long axis, covering the first four nanoislands under the waveguide (see Fig. 3h) for visual of waveguide position). The pulse begins at 50 ps and the magnetization is recorded every 25 ps for 800 time steps, a total simulation time of 40 ns.

For both RMC simulations, the damping parameter α was reduced to 0.006 for greater correspondence with experiment. Simulation cell sizes of 5 nm were used in all dimensions.

Reconfigurable magnonic filter

A quasi-infinite array is simulated using periodic boundary conditions, with a two-column, seven island per-column unit cell. Spin-waves are excited by an out-of-plane HExt sinc pulse applied uniformly across the array, exciting modes between 0.1 and 25 GHz. Simulation cell sizes of 3 nm × 2.2 nm × 5 nm were used in the x, y and z directions respectively.

Magnons are excited with a 20 mT sinc pulse in the z-direction, exciting modes up to 25 GHz. The function is applied across the entire system. The pulse begins at 50 ps and the magnetization is recorded every 20 ps for 256 time steps, a total simulation time of 5.12 ns.