Abstract
A neuron that extracts directionally selective motion information from upstream signals lacking this selectivity must compare visual responses from spatially offset inputs. Distinguishing among prevailing algorithmic models for this computation requires measuring fast neuronal activity and inhibition. In the Drosophila melanogaster visual system, a fourth-order neuron—T4—is the first cell type in the ON pathway to exhibit directionally selective signals. Here we use in vivo whole-cell recordings of T4 to show that directional selectivity originates from simple integration of spatially offset fast excitatory and slow inhibitory inputs, resulting in a suppression of responses to the nonpreferred motion direction. We constructed a passive, conductance-based model of a T4 cell that accurately predicts the neuron’s response to moving stimuli. These results connect the known circuit anatomy of the motion pathway to the algorithmic mechanism by which the direction of motion is computed.
Similar content being viewed by others
Main
The computation of directional selectivity has been studied for decades in both vertebrate and invertebrate visual systems and has given rise to competing algorithmic models1. The Hassenstein–Reichardt (HR) detector uses a synergistic combination of offset excitatory inputs2 to enhance responses to motion in the preferred direction, whereas the Barlow–Levick (BL) detector uses inhibitory input to ‘veto’ an offset excitatory input3, suppressing motion in the nonpreferred, or null, direction.
The HR detector, which was originally formulated to account for motion detection in insects, has become a canonical example of a neuronal computation1,4. This model has endured because its elegant mechanism accounted for a wide array of behavioral results2,5,6 and for the detailed response properties of large motion-sensitive output neurons of the fly visual system1,7,8. Recent progress on the visual circuits upstream of these motion sensitive neurons in Drosophila has revealed that stimuli are processed through ON and OFF pathways9,10,11,12,13,14. In the ON pathway, the columnar T4 neurons are the first cell type to exhibit directionally selective signals10,11,14,15; four T4 subtypes are each directionally selective in one of four cardinal directions9,11,16.
A prevalent hypothesis for how T4 cells could implement the HR detector was proposed based on different input cell types providing the temporally14 and spatially9 offset inputs, but further analysis of the circuit15,17 has ruled out this circuit mechanism. The other recent approach to identifying the mechanism responsible for directional selectivity in the T4 circuit has been to use calcium imaging to measure T4 responses to structured visual stimuli. Several studies found evidence for enhanced responses to preferred-direction motion18,19, while several others found both preferred-direction enhancement and null-direction suppression20,21,22. A number of groups have recently proposed that motion detection in flies may be implemented as a hybrid mechanism featuring elements of both the HR and BL algorithms15,21,22,23. However, direct evidence for either mechanism has been elusive, in large part because these studies rely on calcium imaging. Calcium indicator responses are insensitive to fast events, obscuring the small timing differences required by the HR detector, and are also insensitive to hyperpolarization, thereby preventing the direct measurements of inhibition, a defining feature of the BL model.
Results
To directly measure the physiological properties of T4 neurons, we used targeted in vivo whole-cell electrophysiology. We confirmed the identity of GFP-labeled T4 neurons by measuring reliable depolarizations in response to small ON flashes (Fig. 1a and Supplementary Fig. 1). We used online stimulus generation and analysis to localize the center (within ~2°) of the receptive field (RF) of each recorded neuron (Supplementary Fig. 1b,c). To measure directional selectivity in single T4 cells, we presented a narrow (~2° wide) ON bar moving in eight different directions through the mapped RF center (Fig. 1b,c). The T4 membrane potential showed small depolarizations in response to several directions of motion (Fig. 1b) but large responses to movement in a ~90° range, centered around the preferred direction (PD; opposite to the null direction, ND), in agreement with the tuning width measured with calcium imaging11. Our moving-bar stimulus generates apparent motion: the bar appears to move in a series of discrete (~2°) steps, where the speed of movement is determined by the duration the bar remains at each position. To examine the computation of directional selectivity across a behaviorally relevant range, we presented four movement speeds. The responses to the moving stimuli were averaged across individual recordings once aligned to the PD (Fig. 1c). We quantified the strength of directional selectivity using a directional selectivity index (DSI, defined in Methods) and saw significant tuning at all stimulus speeds (P < 0.05, one sided unpaired t test), with stronger directional selectivity at the two slower speeds (P < 0.05, one sided paired t test; Fig. 1d). At slow speeds, the membrane potential exhibited prominent hyperpolarizing responses, both following the response to PD motion and preceding the depolarizing response to ND motion (Fig. 1c; detailed in Supplementary Fig. 2). The sequence of depolarizing and hyperpolarizing signals depended on the direction of motion, suggesting that inhibitory and excitatory inputs to T4 may be spatially offset, in agreement with recent anatomical findings17.
a, Top: schematic of Drosophila visual system with example T4 cell; whole-cell recordings are targeted to cell body. Bottom: a moving bar (1 × 9 LEDs) is presented as a sequence of discrete steps. b, Responses to a bright bar moving in eight directions (indicated by arrows) at 28°/s. Individual trial responses in gray (n = 3 trials); mean in maroon. Center: response to each direction at the time of maximal directional selectivity. c, Baseline-subtracted responses (n = 17 cells) to bar motion, aligned to the PD of each cell (mean ± s.e.m.). Arrows represent the direction of stimulus motion. Arrowheads indicate hyperpolarization following (or preceding) response to PD (or ND) motion. Colored horizontal bars indicate stimulus presentation. d, DSI for bar motion responses (n = 17 cells). Crosses represent outliers, and triangles denote data points outside of the plot (see Methods for boxplot conventions).
Mapping the T4 receptive field reveals a spatiotemporal asymmetry
In order to characterize the fine structure of the T4 RF, we first localized the RF center and identified the PD–ND axis. We decomposed the moving-bar stimulus into its elementary components—single-position bar flashes with a fixed duration—and presented them at all positions, randomly interleaved, along the PD–ND axis. Aligning the single-position flash responses (SPFRs) based on the position of peak depolarization (Fig. 2a) revealed two key properties. (i) The center and leading side of the T4 RF exhibited excitatory responses. These responses were larger and lasted longer for longer flash stimuli (corresponding to slower speeds). Additionally, longer flashes presented on the leading side of the RF revealed depolarizing responses that were not observed for short flashes. (ii) The inputs along this axis were spatially asymmetrical; hyperpolarizing inputs only appeared on the trailing side of the RF (most clearly seen for the longer duration flashes). Overlaying voltage traces from leading and trailing RF positions exposed a temporal asymmetry in the inputs (Fig. 2b,d). Responses on the trailing side decayed faster than responses at equivalent positions on the leading side. This temporal sharpening can be seen across speeds, including the shortest duration flash where hyperpolarization was not directly recorded (Fig. 2b).
a, Averaged baseline-subtracted responses (mean ± s.e.m.) to single-position bar flash stimuli (top) along the PD–ND axis of each cell (n = 17 cells). b, Mean responses from indicated positions in a, aligned to stimulus presentation (gray rectangles). Arrowheads emphasize differences in decay times. c, Maximum depolarizing and hyperpolarizing responses (mean ± s.e.m.) by stimulus position for 80-ms flashes (n = 17 cells). d, Response-onset time and decay time to flashes near the RF center (medians and quartiles). Cell numbers vary for each position and duration combination (see Methods). e, Slope of the linear regression of onset time against position and the slope of the decay time against position, calculated separately for each cell and each duration (n = 17, 17, 14, 9 cells; * indicates slope < 0 with P < 0.01, one-sided unpaired t test; gray crosses represent outliers; see Methods for boxplot conventions).
For the longer-duration flash stimuli, our RF mapping (Fig. 2c and Supplementary Fig. 3) shows a spatially offset distribution of depolarizing and hyperpolarizing inputs to T4, with the hyperpolarizing input on the trailing side of the RF. Notably, the offset between the peaks of excitatory and inhibitory inputs (~6° of visual angle; Supplementary Fig. 3b) corresponds to the approximate angular separation between adjacent ommatidia on the fly eye, matching the predicted structure for the inputs of the Drosophila motion detector5. Because we did not measure excitatory and inhibitory currents directly, the underlying overlap between excitation and inhibition is expected to extend beyond positions where we can reliably measure hyperpolarizing input.
If T4 implements an HR-like mechanism, we expect that SPFRs on the leading side of the RF would be time-delayed relative to trailing-side SPFRs2,14. A simple expectation for relative time delays between offset visual stimulation generated through differential filtering by either upstream cells and/or synaptic transmission is that the responses would occur with a relative temporal offset. However, the onset time of the flash response was constant across the RF (Fig. 2d,e). Nevertheless, a significant position effect was seen in the decay time (Fig. 2d,e), which we attribute to temporal sharpening (Fig. 2b) due to overlapping inhibitory inputs on the trailing side of the RF (Fig. 2c). Rather than a relative time delay between offset inputs, we find that the temporal differences in the SPFRs can be explained by fast excitatory inputs on the leading side combined with slower inhibitory inputs on the trailing side of the RF.
Directional selectivity results from ND suppression
The classical models for motion detection use a nonlinear combination of offset inputs, resulting in either an enhancement of PD responses (HR) or a suppression of ND responses (BL). A simple test for directional selectivity is to deliver flash stimuli at two positions in the T4 RF and examine whether the response to sequential stimulation in one direction is larger than the response to the opposite sequence of stimulation. We implemented this two-step apparent-motion stimulus using single-position flashes (160 ms in duration) for pairs of positions around the RF center (Fig. 3a). To assess the effect of direction, we compared each two-step response to the superposition of the corresponding two single-position responses (offset in time and summed; Fig. 3b). This comparison revealed no enhanced response to the second bar appearing toward the PD but a reduction in the second bar response when it appears toward the ND. Flashes separated by ~10° (bottom row) did not appear to interact, showing neither enhancement nor suppression. Furthermore, the suppression was most prominent for bar pairs ‘moving’ in the ND that begin on the trailing side, consistent with our finding that the distribution of inhibitory inputs is skewed towards this side of the RF. By comparing the apparent-motion responses to the same bar pairs but in opposite directions (Fig. 3c), we found that the leading side of the RF—corresponding to the primarily excitatory domain of the SPFRs (Fig. 2)—was motion blind (see also Supplementary Fig. 4). Strong directional selectivity was only seen for the bar pairs that included the trailing side of the RF and was only produced by ND suppression.
a, Averaged baseline-subtracted responses (mean ± s.e.m.) to 160-ms flash stimuli presented along the PD–ND axis (n = 3 cells). Single-position responses are shown along the diagonal; PD motion (red) and ND motion (blue) are shown in the lower and upper triangles, respectively. Stimulus positions indicated correspond to those in Fig. 2. Apparent motion is presented as two flash stimuli timed to appear as instances of a bar moving at 14°/s. Space–time plots of the stimuli are depicted in each inset. b, Comparison of mean measured responses to two-step stimulation to the superposition (time-aligned sum) of the single-position responses. Each row shows responses to stimuli presented at the same positions but in the reversed temporal order. Arrow shows magnitude of ND supression. c, Mean PD and ND responses from the corresponding rows in b are compared, with DSI indicated. DSI values are averaged from 3 cells (individual values for top panel: 0.02, 0.06, 0.1; for middle panel: 0.47, 0.5, 0.16).
The superposition of stationary responses generates directional selectivity
The two-step apparent-motion responses (Fig. 3) suggest that it is the integration of offset excitatory and inhibitory inputs that generates directionally selectivity. However, is this mechanism sufficient to explain the directionally selective responses to moving bars? To address this question, we compared the responses to moving-bar stimuli, comprised of an ordered sequence of single-position bar flashes (Fig. 4a,b), with the superposition of SPFRs (summed after appropriate temporal alignment; Fig. 4c). Notably, the only difference between the summed PD and the summed ND responses was the order in which the SPFRs were aligned. This comparison is conceptually similar to our treatment of the two-step apparent-motion responses but probes more interactions across the entire receptive field. We find that the simple sum of SPFRs (Fig. 4c) captures the essential dynamics of the moving-bar response (Fig. 4c,d) and shows significant directional selectivity at all four speeds (Fig. 4e).
a, Schematized T4 dendrites overlaid on nine bar-stimulus positions (colors as in Fig. 2). b, Mean PD and ND motion responses from an example cell to the 28°/s bar motion. c, Top: SPFRs from the example cell in b colored by position, temporally aligned to account for moving-bar position. Bottom: summed SPFRs for PD and ND motion. d, Comparison of mean measured moving bar responses and mean summed SPFRs (n = 31 trajectories, 16 cells). e, Boxplots of DSI values for measured and summed responses across speeds (mean ± s.e.m.; n = 31 trials, 16 cells; see Methods for boxplot conventions). Crosses represent outliers; triangle denotes a point outside the scope of the plot (* indicates DSI > 0 with P < 0.01, one-sided unpaired t test). f, As in d but juxtaposing measured responses and summed SPFRs for PD and ND motion separately (mean ± s.e.m.).
The summed responses approximated the measured responses without any nonlinear integration, an unexpected result as both the HR and BL models of motion detection require a nonlinear interaction to compute directional selectivity. To be clear, we are not claiming that directional selectivity emerges from linear operations (for example, the DSI computation is nonlinear); rather we emphasize that these directionally asymmetric responses expose a significant discrepancy between the T4 mechanism and the classical models. To gain further insight, we examined features of the SPFRs for contributions to directional selectivity in the summed responses and found that it is the position-dependent differences (such as the response shape, sign and magnitude) that account for the DSI of the summed responses (Supplementary Fig. 5). However, the summation of aligned SPFRs only accounted for approximately half of the measured T4 DSI (Fig. 4e). Summing negative and positive potentials undercounts the effect of inhibition. For example, in shunting inhibition, a small inhibitory current can eliminate a much larger excitatory current. The effect of this undercounting is most prominently seen in the overestimated ND responses (Fig. 4f). Does this mismatch suggest that T4 implements a nonlinear step like the classical models, or could biophysically realistic integration of inhibitory inputs explain the additional measured DSI?
A conductance-based simulation quantitatively predicts the T4 motion response
To answer this question, we built a conductance-based model of a T4 neuron reconstructed from electron microscopy data (Fig. 5a). In our model, we randomly distributed excitatory and inhibitory synapses along the dendritic arbor of the cell but fit the synaptic strengths, the time course of the excitatory and inhibitory conductance changes, and the membrane and axial resistivity using an optimization procedure that minimizes the error between simulated responses to bar flashes and our measured SPFRs (from all positions and all speeds; Fig. 5a and Supplementary Fig. 6a–c). We then used the resulting model to simulate the T4 response to a moving bar (Fig. 5b). Notably, we fit our model’s parameters using responses to stationary stimuli (the SPFRs) but used the model to predict the responses to an independent motion stimulus (the moving-bar responses), thus testing the generalization of this model.
a, Anatomical reconstruction of a T4 cell used in the simulation, with expanded dendrite showing positions of modeled excitatory (dark green) and inhibitory (light green) synapses. Enlarged markers indicate active synapses for an example stimulus position. Spatial filters, which determine synaptic weight, are shown normalized and aligned to the dendrite, and temporal filters are shown in inset. b, Mean measured motion responses (from Fig. 4) compared to the simulated predictions. c, Peak PD and ND responses measured in T4s, compared to the summed SPFRs (from Fig. 4) and simulation results. d, DSI for the mean measured responses compared to: (left) model simulation results and summed responses; (center) simulation results without inhibition; (right) simulation results with all synaptic inputs placed in same location, and a separate single-compartment simulation (detailed in Methods).
In comparison to the summed responses (Fig. 4d), the simulated responses more accurately reproduced the measured responses to both PD and ND motion (Fig. 5b,c). Furthermore, the same simulation qualitatively reproduced the dynamics of T4 responses (Fig. 5b) and quantitatively reproduced the magnitude of the directionally selective responses (Fig. 5c,d and Supplementary Fig. 6d–f) at all tested speeds, suggesting that the same mechanism can account for directional selectivity, even at the fastest speeds tested where hyperpolarization was not directly measured (Fig. 2).
One classical neuronal computation of directional selectivity, based on passive cable properties24, is that sequential depolarization directed toward the (thicker) axon generates stronger responses than activation in the opposite direction. To test whether this mechanism could contribute to directional selectivity in T4, we zeroed all inhibitory conductance changes in our model. When the simulation was repeated, only the excitatory synapses were activated as the ‘stimulus’ swept in the PD or ND. We found that in the absence of inhibition, the DSI of the simulated T4 is abolished at all speeds (Fig. 5d), indicating that depolarizing inputs alone cannot produce directional selectivity. This suggests that inhibitory inputs to T4, in addition to providing the slow hyperpolarization that characterizes responses to slow motion (Fig. 1c), also establish the temporal sharpening of trailing side responses, critical for directional selectivity at faster speeds (Supplementary Fig. 5b).
The striking retinotopic alignment of T4 dendrites with the PD–ND axis was an important anatomical clue in their identification as directionally selective cells9,25. We used our simulation to test whether the neuron’s morphology substantially contributes to directional selectivity. By positioning all 154 synaptic inputs (inhibitory and excitatory) at the base of the dendrite (all other parameters held constant), we found that these simulation results are almost indistinguishable from the unmodified simulation (Fig. 5d). As a consequence of this result, we expected that a single-compartment neuron simulation should also be able to capture the response dynamics of T4. Indeed, this simpler model reproduces the moving-bar responses of T4 with only negligible differences from the multicompartment simulation results (Fig. 5d). These results suggest that the critical role of the elaborate and directional T4 dendrite is limited to collecting different input signals across a small region of the fly’s eye. Taken together, these modeling results corroborate our central finding that inhibitory inputs sculpt the essential asymmetry for directionally selective responses in T4 cells; no additional mechanisms are required.
Discussion
We used intracellular recordings to probe the mechanism of directionally selectivity for ON motion in T4 neurons. Using online stimulus generation, we finely mapped the receptive field of T4 neurons (Fig. 2). Notably, this RF structure, comprised of responses to stationary ON bars, can be used to predict the response of T4 to moving bars (Fig. 4). We then improved these predictions with a parsimonious biophysical model integrating offset excitatory and inhibitory conductances (Fig. 5).
In the present study, we show that directional selectivity in T4 neurons arises solely from ND suppression. Recent studies that used calcium imaging of T4 neuron responses to a two-step apparent-motion stimulus found evidence for PD enhancement18,19 or for both PD enhancement and ND suppression20,22. These discrepancies may arise from differences in the stimulus design, differences between single-neuron and population recordings, differences between measurements of membrane potential versus calcium indicator fluorescence, or from combinations of these factors. Since the transformation between membrane potential and calcium indicator fluorescence is likely to be superlinear21, measured calcium responses may appear enhanced when compared to their summed components, even when the underlying voltage response does not show this enhancement (Supplementary Fig. 7). However, as Fisher et al.18 controlled for this possibility, we believe that the difference is most likely explained by differences in stimulus design (centered bars versus edges18; centered narrow bars versus centered wider spots20). Haag et al.20 found PD enhancement in T4 cells, but only for stationary stimuli wider than those used here. These larger stimuli, in addition to strongly depolarizing the measured T4 cells, also effectively stimulate neighboring T4 cells. But since T4 neurons synapse onto other T4 cells with exquisite precision—only cells with the same directional tuning are connected and only along the direction of preferred motion17—this circuit mechanism should produce a superlinear response in one direction (along the PD), but not in the opposite direction. This enhancement of PD motion over a slightly larger spatial scale appears to be evidence for directed facilitation from neighboring T4 cells but not for an HR-like mechanism responsible for directional selectivity (since blocking synaptic transmission in T4 neurons does not substantially reduce directionally selective responses in T4 cells15,22). This factor may partially explain the measurement of PD enhancement in Fisher et al.18, but future experiments will be required to clarify these discrepancies.
Anatomical studies have shown that dendrites of T4 cells are aligned with the PD9,25 and receive spatially offset synaptic inputs from distinct columnar neuron types17. The arbors span several (3–4) retinotopic columns in the medulla16, which, given the ~5° visual angle per column, corresponds well to our measured RF width of ~20° (Fig. 2). The cholinergic columnar neurons Mi1 and Tm3 preferentially synapse onto T4 in the central to distal part of the arbor, while the GABAergic neurons Mi4, C3 and CT1 synapse mainly onto the base of the dendrite15,17,26,27. This anatomical arrangement agrees remarkably well with the functional organization of our measured T4 receptive field, with leading-side excitation and trailing-side inhibition.
A recent study from our lab used circuit perturbations to also propose a hybrid mechanism for T4 motion responses15. Although we showed nonlinear integration of excitatory inputs by T4, we did not show that this nonlinearity contributes to the computation of directional selectivity, so these results do not conflict with the current findings. In fact, electron microscopy–based circuit analysis9,17, as well as a number of functional studies14,15,23,26,28,29, suggests that multiple cell types (at least Mi1 and Tm3) contribute to the excitatory ON component of our measured RF, without evidence for a spatial offset required for an HR-like mechanism17. In our previous study, we also showed that silencing one of the main inhibitory inputs to T4 (Mi4) does not reduce directional selectivity15. Since our current results strongly suggest that inhibition is necessary for computing directional selectivity, it is entirely possible that the critical inhibitory inputs to T4 are not simply contributed by a single cell type (other candidates include CT1, C3 and TmY1517).
Synthesis of experimental results with classical computational models for motion detection
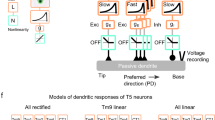
Historically, the computation of directional selectivity has been conceptualized with algorithmic models outlining the general properties that transform nonselective inputs into a directionally selective output. Here we compare our results with the implications of the classical models and present an algorithmic summary of our findings. Motion-detector models typically describe a ‘fully opponent’ computation, whereby local motion estimates in opposing directions are subtracted to minimize nonmotion signals1. Since T4 is now understood to reside one step before this opponent subtraction30, we only consider the subunits of each model type before this subtractions stage. The classical model for insect motion detection is the HR detector2. This detector generates directional selectivity by delaying leading-side excitatory input and combining it with trailing-side excitatory input with a nonlinear amplification, thus enhancing the PD response (Fig. 6a). If T4 directional selectivity was based on an HR-like mechanism, we would expect to find (i) excitatory inputs spanning the receptive field, (ii) differing temporal filtering of inputs resulting in a delayed leading side and (iii) enhanced responses to PD motion (Fig. 6a). We did not find evidence for any of these properties: (i) T4 receives offset excitatory and inhibitory inputs (Fig. 2c), (ii) leading side responses are not temporally delayed (Fig. 2d, e and Supplementary Fig. 8), and (iii) PD motion is not enhanced (Figs. 3, 4 and 5). Furthermore, the excitatory region of the receptive field is motion blind (Supplementary Fig. 4).
a, The HR detector2 uses slower filtering on the leading side arm and a multiplicative nonlinearity to produce coincidence detection of excitatory signals. The time constants are labeled as 𝝉E-Lead and 𝝉E-Trail, where E indicates filtering of an excitatory leading (lead, L) or trailing (trail, T) signal. The semicircles represent two neighboring inputs to the motion detectors. b, The BL detector3 combines a slow trailing-side inhibitory (I) arm with a faster leading-side excitatory (E) arm through an AND–NOT operation that vetoes motion in the null direction. c, The AB detector31 uses oriented spatiotemporal filters, created from offset spatial and fast and slow temporal filters, to produce directional selectivity. d, A summary of the T4 mechanism formatted for comparison to the algorithmic models, based on the Torre–Poggio model35. The simple RF structure of T4 (Supplementary Fig. 8) does not require the more complex spatial and temporal filters used in the AB model. Instead we use filters fit to T4 measurements (Fig. 5), which produce a fast, excitatory leading signal and a delayed, inhibitory trailing signal. As in the AB model, directionally selective responses can be obtained through a linear combination of these signals (gray lines). The dynamic nonlinearity operates on the magnitude of excitatory (E) and inhibitory (I) conductances (detailed in Methods) to produce a directionally selective membrane potential response.
An alternative classical model is the BL detector3, which integrates fast leading-side excitation and slower trailing-side inhibition through the nonlinear ‘AND–NOT’ operation (Fig. 6b). Directional selectivity is computed when excitatory input precedes the inhibitory input; in the reverse order, ND motion is suppressed. We find several properties in our T4 recordings that agree with this framework: (i) leading-side excitatory responses and trailing-side inhibitory responses (Fig. 2), (ii) longer temporal filtering on the trailing side, such that inhibition outlasts excitation (Figs. 2 and 5 and Supplementary Fig. 8) and (iii) clear evidence for ND suppression with both two-step and moving-bar apparent motion (Figs. 3c and 4f).
While the organization of the T4 RF agrees with the algorithmic principle of the BL model, we find an important difference in the integration mechanism. The BL model uses a strong nonlinearity and so does not produce directionally selective responses from the superposition of the responses to stationary inputs (which our T4 recordings show; Figs. 3 and 4). This seemingly technical distinction is in fact quite consequential, because in both the HR and BL models, the nonlinearity is a defining characteristic: without it, there are no directionally selective responses. In contrast, our T4 results show that directional selectivity is already present in the superposition of the stationary stimulus responses.
A third class of motion detectors—the Adelson–Bergen (AB) motion–energy model31—generates directional selectivity using filters that are oriented in space and time. These linear filters are combined spatial and temporal filters that feature a prominent space–time tilt indicating the preferred direction. In Fig. 6c we present only the relevant subunit of the full AB model for comparison with our data. This subunit has (i) different spatial filters on each of its arms, (ii) excitatory and inhibitory inputs, (iii) a linear integration step that produces a directionally selective response from the superposition of stationary responses (as seen in simple cells of the cat visual cortex32) and (iv) a static, amplifying nonlinearity. This flexible model, whose commonalities with variants of the classical motion-detection models have been broadly discussed1,31,33, provides a useful framework for representing the T4 computation.
In light of the commonalities and discrepancies between classical algorithmic models and our results, we next provide a summary of our understanding of T4 in a format that is directly comparable to these models (Fig. 6d), with an excitatory and an inhibitory arm. The more complex spatial and temporal filters of the AB model, selected to match cortical recordings, are replaced with the filters describing T4 responses (Fig. 5 and Methods). The spatial filters create the leading-versus-trailing offset and the temporal filters create the fast-versus-slow difference between the excitatory and inhibitory arms. In contrast to the ‘point-sampling’ inputs of the classical HR and BL models, T4 shows spatially extended responses to visual input (Fig. 2b), which has previously been shown to improve the accuracy of motion detection34. While the sum of the linear filter outputs produces asymmetric responses to PD and ND motion (Fig. 6d), T4 neurons further enhance this selectivity through nonlinear integration. While the AB model employs a static, amplifying nonlinearity, we measure a suppressing nonlinearity that is well approximated with a simplified passive, biophysical model (similar to a previous formulation35; Figs. 5d and 6d, and see Methods).
Spatiotemporal receptive fields of T4 cells
Representing the response properties of neurons using spatiotemporal receptive fields, equivalent to the responses of the spatiotemporal filters in the AB model, has provided significant insight into transformation along the visual pathway of mammals36 and has recently also been applied to the responses of directionally selective neurons in flies19,21. We replotted the averaged SPFRs to approximate the spatiotemporal receptive field of a T4 neuron (Supplementary Fig. 8). As expected for a directionally selective neuron, we found a distinctive tilt in this receptive field, indicating the PD. This RF has both excitatory and inhibitory lobes, which both appear tilted, an organization that may suggest a PD-enhancing and ND-suppressing mechanism19,21. To explore the basis of the RF tilt, we used our multicompartment T4 model and replotted the simulated SPFRs (Supplementary Fig. 6c) as a spatiotemporal RF (Supplementary Fig. 8). Since the model was fit to the SPFR data, the qualitative agreement between these RFs is not surprising. The simulated RF also features a tilted excitatory lobe. When we removed inhibition in our model (Fig. 5d) and reproduced the RF (Supplementary Fig. 8), we found that the excitatory lobe was no longer tilted, consistent with our inference that inhibition sharpens trailing-side responses (Fig. 2b). This simulation shows that a tilted, two-lobed spatiotemporal RF does not necessarily support a hybrid mechanism and reiterates the lack of evidence in our data for PD enhancement.
It is worth noting that the receptive fields of T5 cells, the OFF directionally selective neurons, look qualitatively similar to those estimated for T4 neurons19,20,21. Therefore, it is possible that T5 neurons compute directional selectivity using the same simple mechanism that we have established here for T4 neurons. Notably, no small-field inhibitory inputs37,38 to T5 have thus far been identified, raising the possibility of different implementations of the same motion computation in ON and OFF pathways39,40.
Methods
Histology
To visualize the expression pattern of the T4 driver line (SS02344), brains of female flies were immunolabeled and imaged as described41. Anti-Brp was used as a stain for the neuropil marker (anti-nc82, 1:30, Developmental Studies Hybridoma Bank) and pJFRC225-5XUAS-IVS-myr::smFLAG (rat anti-FLAG, 1:100, Novus Biologicals) in VK00005 42 was used as the reporter for GAL4 expression. The image shown in Supplementary Fig. 1a was generated from a confocal stack imaged on a Zeiss LSM 710 microscope with a 63× objective, and resampled using Vaa3D43.
Electrophysiology
Experiments were performed on 1- to 2-d old female Drosophila melanogaster (flies were reared under constant light conditions at 24 °C; some flies experienced periods of darkness, including overnight, before dissection). To target T4 cells, a single genotype was used: pJFRC28-10XUAS-IVS-GFP-p1044 in attP2 crossed to stable split-GAL4 SS02344 (VT015785-p65ADZp (attP40); R42F06-ZpGdbd (attP2), generously provided by A. Nern in G. Rubin’s laboratory, Janelia; line details with expression data available from http://splitgal4.janelia.org/). Flies were briefly anesthetized on ice and transferred to a special chilled vacuum holder where they were mounted, with the head tilted down, to a customized platform machined from PEEK using UV-cured glue (Loctite 3972). CAD files for the platform and vacuum holder are available upon request. To reduce brain motion, the proboscis was fixed to the head with a small amount of the same glue. The posterior part of the cuticle was removed using syringe needles and fine forceps. The perineural sheath was peeled using fine forceps and, if needed, further removed with a suction pipette under the microscope. To further reduce brain motion, muscle 1645 was removed from between the antenna.
The brain was continuously perfused with an extracellular saline containing (in mM): 103 NaCl, 3 KCl, 1.5 CaCl2, 4 MgCl2, 1 NaH2PO4, 26 NaHCO3, 5 N-Tris (hydroxymethyl) methyl-2-aminoethane-sulfonic acid, 10 glucose and 10 trehalose46. Osmolarity was adjusted to 275 mOsm, and saline was bubbled with 95% O2 / 5% CO2 during the experiment to reach a final pH of 7.3. Pressure-polished patch-clamp electrodes were pulled for a resistance of 9.5–10.5 MΩ and filled with an intracellular saline containing (in mM): 140 KAsp, 10 HEPES, 1.1 EGTA, 0.1 CaCl2, 4 MgATP, 0.5 NaGTP and 5 glutathione46. We added 250 μM Alexa Fluor 594 hydrazide to the intracellular saline before each experiment, to reach a final osmolarity of 265 mOsm, with a pH of 7.3.
The mounted, dissected flies were positioned on a rigid platform mounted on an air table. Recordings were obtained from labeled T4 cell bodies under visual control using a Sutter SOM microscope with a 60× water-immersion objective. To visualize the GFP-labeled cells, a monochrome, IR-sensitive CCD camera (ThorLabs 1500M-GE) was mounted to the microscope, an IR LED provided oblique illumination (ThorLabs M850F2), and a 460-nm LED provided GFP excitation (Sutter TLED source). Images were acquired using Micro-Manager47 to allow for automatic contrast adjustment.
All recordings were obtained from the left side of the brain. Current-clamp recordings were low-pass filtered at 10 kHz using an Axon MultiClamp 700B amplifier, and were sampled at 20 kHz (National Instrument PCIe-7842R LX50 Multifunction RIO board) using custom LabView (2013 v.13.0.1f2; National Instruments) and Matlab (2015a; MathWorks) software. The membrane potential of recorded cells was set around –65 mV (uncorrected for liquid junction potential), which required injecting a small, hyperpolarizing current (0–3 pA), which after initial adjustment was maintained at a constant value throughout the recording. To verify recording quality, current-step injections were performed intermittently throughout the experiment. Recordings from cells in which either visual or current-step responses diminished noticeably were terminated.
Visual stimuli
The display was constructed from an updated version of the LED panels previously described48. The arena covered slightly more than one half of a cylinder (216° in azimuth and ~72° in elevation) of the fly’s visual field, with the maximum pixel diameter subtending an angle of ~2.25° on the fly eye. Green LEDs (emission peak: 565 nm) were used; bright stimuli were ~72 cd/m2 and were presented on an intermediate intensity background of ~31 cd/m2.
Visual stimuli were generated using custom-written Matlab code that allowed rapid generation of stimuli based on individual cell responses. In contrast to the published stimulus control system48, we have now implemented an FPGA-based panel display controller, using the same PCIe card (National Instrument PCIe-7842R LX50 Multifunction RIO board) that also acquired the electrophysiology data. This new control system (implemented in LabView) streams pattern data directly from PC file storage, allowing for online stimulus generation. Furthermore, this new control system featured high-precision (to 10 μs) timing and logging of all events, enabling reliable alignment of electrophysiology data with visual stimuli.
To map the receptive field (RF) center of each recorded cell, three grids of flashing bright squares (on an intermediate intensity background) were presented at increasing resolution. Each flash stimulus was presented for 140 ms. First, a 6 × 7 grid of non-overlapping bright squares (5 × 5 LEDs; ~11° × ~11°) was presented. If a response was detected, a denser 3 × 3 grid with 50% overlapping bright and dark squares (5 × 5 LEDs; ~11° × ~11°), to further verify that these were T4 cells, was presented at the estimated position of the RF center. The dark squares were used to further verify that the recorded cells were T4, and not T5, cells (see Supplementary Fig. 1). If a recorded cell was consistently responsive to the first two mapping stimuli, a third one was presented to identify the RF center. A 5 × 5 grid of 3 × 3 LED bright squares separated by single-pixel shifts was presented at the estimated center of the second grid stimulus. The location of the peak response to this stimulus was used as the RF center in subsequent experiments. Once the RF center was identified, the moving bar stimulus was presented in eight directions and four step-durations. The bar was 1 × 9 pixels. When moving in the cardinal directions, the motion spanned 9 pixels. In the diagonal directions, bar motion included more steps to cover the same distance (9 steps vs. 13 steps). Once the preferred direction had been estimated, bright bar (also 1 × 9 pixels) flashes were presented on the relevant axis. To verify full coverage of RF, this stimulus was presented over an area larger than the original motion window (at least 13 positions). In addition to these stimuli, most cells were also presented with additional stimuli following this procedure. All stimuli were presented in a pseudorandom order within stimulus blocks. All stimuli were presented three times, except for single-bar flashes, which were repeated five times. The interstimulus interval was 500 ms for moving stimuli and 800 ms for single-bar flashes (to minimize the effect of ongoing inhibition on the responses to subsequent stimuli).
Analysis
All data analysis was performed in Matlab using custom written code. Since the T4 baseline was typically stable, we included only trials in which the mean prestimulus baseline did not differ from the overall prestimulus mean for that group of stimuli by more than 10 mV. We also verified that the prestimulus mean and overall mean for that trial did not differ by more than 15 mV (or 25 mV for slow-moving bars, due to their strong responses). This was designed to identify those rare trials in which the trace became unstable only after the stimulus was presented. Responses were later aligned to the appearance of the bar stimulus and averaged (or the appearance of the bar in the central position in case of the eight-orientation moving bar). T4 cells are expected to signal using graded synapses. Consistent with this expectation, we find that T4 recordings only occasionally feature very weak, fast transients (~1–2 mV in size) that could not be verified as spikes. Therefore, we have focused our analysis on the graded (subthreshold) components of T4’s responses.
Determining PD
First, eight-direction responses were aligned to the center position for each cell. Second, for the duration of bar presentation, the mean vector response was calculated for each time point as \(\bar{R}\left(t\right)={\sum }_{k=1}^{8}R\left({{\rm{\theta }}}_{k},t\right){e}^{i{\theta }_{k}}\), with θ k being the direction of motion (in 45° intervals) and R(θ k ,t) the response at that direction at time t. Supplementary Fig. 2 shows the result of this procedure for the normalized vector magnitude and \(\bar{\theta }\) .This procedure can be thought of as mimicking a downstream neuron, receiving input from T4s with the same RF center but different PDs. The \(\bar{\theta }\) value for the cell was selected at the timepoint when the mean vector magnitude was maximal (repeated for four step-durations and averaged). In the polar plot of Fig. 1b, this timepoint is used for the response to each bar direction. The PD was determined as the θ k value with the minimal difference to \(\bar{\theta }\). For Fig. 1c, responses were then circularly shifted to align the PD with rightward motions for plotting and averaging purposes.
DSI calculation
The direction selectivity index was defined as \(R\left(PD\right)-R\left(ND\right)/R\left(PD\right)\), with each response defined as the 0.995 quantile (a robust estimate of the max) within the stimulus presentation window. DSI values for the model and model variations were calculated in the same manner.
Depolarization calculation for single-position flash response
Responses were defined as the 0.995 quantile (a robust estimate of the max) of the response during the time between bar appearance and flash duration +75 ms. If this number did not exceed 3 s.d. of the prestimulus baseline (for all bar flashes for that cell), the response was defined as zero.
Hyperpolarization calcultion for single-position flash response
These responses were calculated as for depolarization except that the time window lasted until end of trial (due to the slower time course for inhibition) and the threshold was 2 s.d. (due to the lower magnitude of hyperpolarization). These calculations were used for Fig. 2c and Supplementary Fig. 3.
Depolarization (or hyperpolarization) normalization
All detected averaged SPFRs for a given duration were normalized to the maximal depolarizing (hyperpolarizing) absolute response for that duration and that cell. Figure 2c shows the average of these normalized responses for a single duration. Supplementary Fig. 3a shows the sums for each cell, for four normalized depolarizing responses and the two slowest hyperpolarizing responses (since hyperpolarization was hard to detect for brief flashes). A position that showed the maximal response for all durations will, therefore, have a value of 4 for depolarizations and 2 for hyperpolarizations.
Onset-time calculation
Data during a window of 200 ms before stimulus presentation from all the single-bar flashes presented to a cell was used for a per-cell estimate of the s.d. of the baseline. Only presentations in which the average SPFR was detected as depolarizing were used for onset-time calculation. Onset time was defined as the time from stimulus presentation (after it was corrected for a small display latency) in which the response crossed 0.5× baseline s.d. This threshold value did not exceed 0.5 mV. This calculation is used in Fig. 2d,e. Because positions in the center of the RF feature a mixture of excitation and inhibition, the peak time is ‘contaminated’ by the inhibitory contribution and could not be used as an independent, reliable measure of the properties of the excitatory input.
Decay time calculation
The decay time (from 80% to 20% of maximal response) was calculated for all cells and all positions in which a depolarizing response was detected. If 20% of max response was not attained by the time recording ended, that data point was excluded. This calculation is used in Fig. 2d,e. The numbers of cells that passed the above threshold and were included in Fig. 2d is, for 160 ms: 17, 17, 17, 17, 17, 15, 9; for 80 ms: 15, 16, 17, 17, 16, 15, 6; for 40 ms: 11, 13, 16, 16, 16, 10, 8; and for 20 ms: 1, 8, 11, 17, 12, 8, 4.
Slope calculation (onset and decay times)
To calculate the slope in Fig. 2e, onset (decay) time values from all the positions of an individual cell were fit with a linear regression. Fits were performed only when more than four positions showed responses, to account for cases in which not all positions showed detectable depolarizing responses (especially due to fast flashes).
Summed SPFRs (superposition)
SPRFs were aligned to the time of the corresponding position appearance in the moving-bar stimulus. Responses were padded with zeros (since all were baseline-subtracted) to extend brief single-bar responses to the timescale of a moving bar. This procedure was used both for the two-step apparent-motion stimuli and for the moving-bar stimuli (Figs. 3 and 4 and Supplementary Figs. 4, 5 and 7). For moving-bar analysis, responses in which hyperpolarization did not return to zero by the end of the recording were padded with a linear fit to the last 250 ms that was extended to zero (to avoid abrupt changes). For the analysis in Fig. 4, one cell was not included because the dataset for this recording was incomplete.
Rectified SPFR sums
These were calculated as for standard sums but with all negative values in individual SPFRs set to zeros (Supplementary Fig. 5b).
Scaled center response SPFR sums
Individual SPFRs were replaced with a central response trace after rectification, scaled to the amplitude of the original positional response. This was done to eliminate the positional change in response width (Supplementary Fig. 5b).
Average traces in Fig. 4d,f and Supplementary Fig. 5a
Positions from all cells were aligned to the center zero position before averaging. All trajectories that were longer than eight positions were included in this analysis. Some were extracted from the original eight-direction stimuli (Fig. 1), which was used to determine PD, and some from additional trajectories that were presented just along the PD axis.
Squared sum in Supplementary Fig. 7
The averaged measured data (presented in Supplementary Fig. 7a) was squared (after baseline-subtraction) for both the individual presentations and the two-step positions. To generate the expected sum, individual squared responses were temporally aligned and summed.
Spatiotemporal maps in Supplementary Fig. 8
Averaged SPFRs were aligned temporally to stimulus appearance. A two-dimensional Gaussian was used to smooth the data both temporally (σ = 250 ms) and spatially (σ = one position) using Matlab function imgaussfilt. Contour plots were generated using Matlab function contourf, with a fixed ‘level list’ that was manually generated to include smaller steps for the hyperpolarized range. An identical procedure was performed on the simulated SPFRs and simulated SPFRs without inhibition (see the “Conductance model” section for details).
Statistics
To determine statistically significant differences, one-sided unpaired Student’s t tests were used for comparing groups (Figs. 2e and 4e and Supplementary Fig. 5b). Data distribution was assumed to be normal, but this was not formally tested. No statistical methods were used to predetermine sample sizes, but our sample sizes are similar to those reported in previous publications49,50,51. Data collection and analysis were not performed blind to the conditions of the experiments.
Data-plotting conventions
All boxplots presented (except Fig. 2d) were plotted with Matlab conventions. Boxes represent the first and third quartiles, center lines represent medians, and whiskers represent the farthest point within the q3 + IQR (or q1 – IQR) range. Boxplots for Fig. 2d depict only medians and quartiles due to spatial constraints. In Fig. 1, triangles denote data points outside of the plot (for 20 ms: –0.19 and –1.14; for 40 ms: –0.09 and –0.7). In Fig. 4e, triangle denotes a data point outside the plot for measured 40 ms: –0.7. Most plots used the cbrewer color library from the MathWorks file exchange.
Conductance model
A model T4 neuron was implemented using the morphology of a single T4 cell, reconstructed from electron microscopy data. The neuron morphology was generously shared by K. Shinomiya and Janelia’s FlyEM project team. The FlyEM team collected a dataset containing approximately half of a Drosophila optic lobe, imaged with isotropic 8-nm voxels by focused ion-beam milling scanning electron microscopy (FIB-SEM). The sample was prepared from the head of a female fly as previously reported, using high-pressure freezing followed by freeze-substituted embedding9,52. A 153 × 85 × 180-μm volume containing connected regions of the lamina, medulla, lobula and lobula plate was imaged. The imaged volume was segmented automatically based on an algorithm similar to one previously described53. NeuTu-EM (https://github.com/janelia-flyem/NeuTu/tree/flyem_release), in which segmented fragments of neurons are merged and split to form the complete morphology of individual neurons, was then used to proofread the segmented volume. A reconstructed T4 neuron was identified based on its distinctive morphology, with dendritic compartments spanning ~20 μm in the medulla and an axon projecting to a distinct layer of the Lobula Plate. The reconstructed neuron morphology contained 344 sections.
To correct for a small number of inconsistencies in the reconstructed morphology, the diameter of each dendritic section was smoothed by performing a moving average of the diameter of five adjacent sections (using the TREES toolbox54). The simulation was implemented and run using NEURON v.7.4 (http://www.neuron.yale.edu/neuron/). Analog synapses were placed randomly throughout the dendritic arbor (this compartment, containing 235 sections, was defined manually), and a recording electrode was attached to the soma. After identifying the primary dendritic axis (used to simulate stimulation along the PD–ND axis), we assigned each dendritic section a value corresponding to its projection on this axis (x*, between 0 and 1). We subdivided the axis into M = 11 intervals, where each interval contains an equal number of dendritic sections (21 sections), to map onto the 11 stimulated positions required to enclose the T4 receptive field. We used 11 intervals because the average traces in Fig. 4d, which were the reference for the simulation, spanned positions –5 to 5 (see “Analysis” subsection). Within an interval, we randomly selected a fixed number N of dendritic sections N E = 9 (or N I = 5) where excitatory (E; or inhibitory, I) graded synapses were placed. The reversal potential for excitatory synapses was set to 0 mV and to –70 mV for inhibitory synapses. The resting membrane potential was set to –65 mV. To simulate a visual input, mimicking the appearance of the bar at one position, all the synapses in the region were activated with conductance dynamics that were uniform for all E and different, but uniform, for all I synapses. Our model simplifies the transformation from visual input to a synaptic conductance change, so while we are not explicitly modeling the optical and neuronal prefiltering that is upstream of T4, these details are implicitly incorporated into the model, as these elements contribute to the SPFRs, which the model was fit to reproduce. To simulate an analog synapse, we used the single-electrode voltage-clamp (SEVC) point process and injected the inverse of our calculated conductance (see below) into the SEVC R s (zero conductance corresponds to 1 × 109 Ω resistance).
We computed the E and I conductance time course at each synapse (g E (t,x*), g I (t,x*)) according to the following:
where C = {E, I}, and (τ C,rise, τ C,decay) denote the rise (or decay) time constants of the synapse, I C(t,x*) is the synaptic input, and a C(x*) scales the conductance based on the location of the synapse on the PD–ND axis. We modeled the amplitude as a Gaussian profile
with an overall amplitude parameter A C, a peak location along the dendrite μ C , and a width σ C . We chose a Gaussian profile because it reasonably approximates the spatial profile of E and I inputs measured for the SPFRs (Fig. 2c and Supplementary Fig. 3a) and to reduce the number of parameters needed to describe the inputs to the simulated T4 neuron. The synaptic input, I C(t,x*), was modeled as a pulse of unit amplitude with duration T, where T = 20, 40, 80, 160 ms, and was identical for all the synapses located within one of the M intervals.
Three additional parameters of the neuronal model are the membrane resistivity (R m), membrane capacitance (C m) and axial resistivity (R a). For all simulations, C m was fixed at C m = 1 μF/cm2. We optimized the remaining model parameters, by performing nonlinear least squares minimization between the numerical simulation results combining all stimulus positions (M = 11 intervals) and durations (T), resulting in 44 simulated SPFR responses, and the corresponding measured SPFRs (Supplementary Fig. 6c). The minimization used the lsqcurvefit() function from Matlab’s Optimization Toolbox. Having fit the model parameters using the single-position flash stimuli, we used the same optimized parameters to simulate the dynamics of the model in response to moving bars (apparent-motion stimulus). The moving-bar stimulus was implemented by sequentially activating the synaptic inputs along the dendritic axis, with each interval being active for a duration T.
Model manipulations
We moved all synaptic inputs (99 excitatory and 55 inhibitory synapses) to the first dendritic section (Fig. 5d). We then removed all conductance changes mediated by the inhibitory synapses, while keeping all other settings of the model fixed. This was accomplished by setting the duration of all inhibitory synaptic inputs to zero (Fig. 5d).
Single-compartment conductance model
We modeled the time course of the membrane potential of a T4 neuron, V(t), according to the single-compartment dynamics
where \({C}_{M}\) is the membrane capacitance, \({g}_{L}\) is the leak conductance (resulting in the integration time constant of the neuron τ V = C M /g L), and V L, V E and V I are the resting, excitatory and inhibitory reversal potentials respectively (values in Supplementary Table 1). The excitatory and inhibitory conductances, \({g}_{{\rm{C}}}\left(t\right),{\rm{C}}=\left\{{\rm{E}},{\rm{I}}\right\}\), were modeled as a Gaussian weighted linear combination of stimulus location-specific conductances, \({g}_{{\rm{C}}}\left(t\right)={\sum }_{i=1}^{M}{a}_{{\rm{C}}}\left({x}_{i}\right){f}_{{\rm{C}}}\left(t,{x}_{i}\right)\) where, as for the model described in the previous section,
g C(t,x i ), the conductance change elicited by the presentation of a stimulus I C(t,x i ) in one of M = 15 locations x i , follows the dynamics
Stimuli had characteristics identical to those described in the previous section. All the parameters (with the exception of the reversal potentials) were optimized to minimize the mean squared error between model responses to single-bar inputs and average T4 SPFRs.
As with our original model, solutions to the single compartment model conformed to one of the two solution clusters. The solutions either had fast (<10 ms) time constants for E and slow membrane time constants (solution cluster 1), or slower E time constants and negligible membrane time constants (solution cluster 2).
When the time constant of the neuron is negligible compared to the time scale of the stimuli and conductances \(\left({\tau }_{V}\to 0\right)\), the relative change of membrane potential with respect to the resting potential can be written as
where \(\alpha =\frac{{V}_{{\rm{L}}}-{V}_{{\rm{I}}}}{{V}_{{\rm{E}}}-{V}_{{\rm{L}}}}\), \(E\left(t\right)={g}_{{\rm{E}}}\left(t\right){\rm{/}}{g}_{{\rm{L}}}\), and \(I\left(t\right)={g}_{{\rm{I}}}\left(t\right){\rm{/}}{g}_{{\rm{L}}}\). This is the expression used in the model schematics depicted in Fig. 6.
Note that if one combination of excitatory and inhibitory conductances elicits a hyperpolarizing response, \(\Delta {V}_{1}=\frac{{E}_{1}-\alpha {I}_{1}}{1+{E}_{1}+{I}_{1}} < 0\)
while a second one produces a depolarizing response, \(\Delta {V}_{2}=\frac{{E}_{2}-\alpha {I}_{2}}{1+{E}_{2}+{I}_{2}} > 0\),
under some conditions it is possible to obtain a supralinear response to the superposition of the two sets of conductances
For instance, when E 1 = 0, I 2 = 0, supralinearity is obtained if \({E}_{2} > \frac{1+{I}_{1}-\alpha }{\alpha }\).
Life Sciences Reporting Summary
Further information on experimental design is available in the Life Sciences Reporting Summary.
Code availability
The essential code used to generate the primary results and conduct the simulations for this study are available at https://doi.org/10.25378/janelia.c.3955843 and https://www.janelia.org/publication/simple-integration-fast-excitation-and-offset-delayed-inhibition-computes-directional.
Data availability
The data used to generate the primary results of this study are available at https://doi.org/10.25378/janelia.c.3955843 and https://www.janelia.org/publication/simple-integration-fast-excitation-and-offset-delayed-inhibition-computes-directional.
The split-GAL4 driver used to target T4 cells (SS02344: VT015785-p65ADZp (attP40); R42F06-ZpGdbd (attP2)) was generously provided by A. Nern (line details with expression data available from http://splitgal4.janelia.org/).
References
Borst, A. & Egelhaaf, M. Principles of visual motion detection. Trends Neurosci. 12, 297–306 (1989).
Hassenstein, V. B. & Reichardt, W. Systemtheoretische Analyse der Zeit-, Reihenfolgen- und Vorzeichenauswertung bei der Bewegungsperzeption des Rüsselkäfers Chlorophanus. Z. Naturforsch. B 11, 513–524 (1956).
Barlow, H. B. & Levick, W. R. The mechanism of directionally selective units in rabbit’s retina. J. Physiol. (Lond.) 178, 477–504 (1965).
Poggio, T. & Reichardt, W. Considerations on models of movement detection. Kybernetik 13, 223–227 (1973).
Buchner, E. Elementary movement detectors in an insect visual system. Biol. Cybern. 24, 85–101 (1976).
Tuthill, J. C., Chiappe, M. E. & Reiser, M. B. Neural correlates of illusory motion perception in Drosophila. Proc. Natl. Acad. Sci. USA 108, 9685–9690 (2011).
Haag, J., Denk, W. & Borst, A. Fly motion vision is based on Reichardt detectors regardless of the signal-to-noise ratio. Proc. Natl. Acad. Sci. USA 101, 16333–16338 (2004).
Borst, A., Flanagin, V. L. & Sompolinsky, H. Adaptation without parameter change: dynamic gain control in motion detection. Proc. Natl. Acad. Sci. USA 102, 6172–6176 (2005).
Takemura, S. Y. et al. A visual motion detection circuit suggested by Drosophila connectomics. Nature 500, 175–181 (2013).
Strother, J. A., Nern, A. & Reiser, M. B. Direct observation of ON and OFF pathways in the Drosophila visual system. Curr. Biol. 24, 976–983 (2014).
Maisak, M. S. et al. A directional tuning map of Drosophila elementary motion detectors. Nature 500, 212–216 (2013).
Joesch, M., Schnell, B., Raghu, S. V., Reiff, D. F. & Borst, A. ON and OFF pathways in Drosophila motion vision. Nature 468, 300–304 (2010).
Clark, D. A., Bursztyn, L., Horowitz, M. A., Schnitzer, M. J. & Clandinin, T. R. Defining the computational structure of the motion detector in Drosophila. Neuron 70, 1165–1177 (2011).
Behnia, R., Clark, D. A., Carter, A. G., Clandinin, T. R. & Desplan, C. Processing properties of ON and OFF pathways for Drosophila motion detection. Nature 512, 427–430 (2014).
Strother, J. A. et al. The emergence of directional selectivity in the visual motion pathway of Drosophila. Neuron 94, 168–182.e10 (2017).
Fischbach, K.-F. & Dittrich, A. The optic lobe of Drosophila melanogaster. I. A Golgi analysis of wild-type structure. Cell Tissue Res. 258, 441–475 (1989).
Takemura, S. Y. et al. The comprehensive connectome of a neural substrate for ‘ON’ motion detection in Drosophila. eLife https://doi.org/10.7554/eLife.24394 (2017).
Fisher, Y. E., Silies, M. & Clandinin, T. R. Orientation selectivity sharpens motion detection in Drosophila. Neuron 88, 390–402 (2015).
Salazar-Gatzimas, E. et al. Direct measurement of correlation responses in Drosophila elementary motion detectors reveals fast timescale tuning. Neuron 92, 227–239 (2016).
Haag, J., Mishra, A. & Borst, A. A common directional tuning mechanism of Drosophila motion-sensing neurons in the ON and in the OFF pathway. eLife 6, e29044 (2017).
Leong, J. C., Esch, J. J., Poole, B., Ganguli, S. & Clandinin, T. R. Direction selectivity in Drosophila emerges from preferred-direction enhancement and null-direction suppression. J. Neurosci. 36, 8078–8092 (2016).
Haag, J., Arenz, A., Serbe, E., Gabbiani, F. & Borst, A. Complementary mechanisms create direction selectivity in the fly. eLife 5, e17421 (2016).
Arenz, A., Drews, M. S., Richter, F. G., Ammer, G. & Borst, A. The temporal tuning of the Drosophila motion detectors is determined by the dynamics of their input elements. Curr. Biol. 27, 929–944 (2017).
Rall, W. Theoretical significance of dendritic trees for neuronal input-output relations. in Neural Theory and Modeling 7397 (ed. Reiss, R. F.) (Stanford University Press, Palo Alto, 1964).
Strausfeld, N. J. & Lee, J. K. Neuronal basis for parallel visual processing in the fly. Vis. Neurosci. 7, 13–33 (1991).
Pankova, K. & Borst, A. Transgenic line for the identification of cholinergic release sites in Drosophila melanogaster. J. Exp. Biol. 220, 1405–1410 (2017).
Long, X., Colonell, J., Wong, A. M., Singer, R. H. & Lionnet, T. Quantitative mRNA imaging throughout the entire Drosophila brain. Nat. Methods 14, 703–706 10 (2017).
Yang, H. H. et al. Subcellular imaging of voltage and calcium signals reveals neural processing in vivo. Cell 166, 245–257 (2016).
Ammer, G., Leonhardt, A., Bahl, A., Dickson, B. J. & Borst, A. Functional specialization of neural input elements to the Drosophila ON motion detector. Curr. Biol. 25, 2247–2253 (2015).
Mauss, A. S. et al. Neural circuit to integrate opposing motions in the visual field. Cell 162, 351–362 (2015).
Adelson, E. H. & Bergen, J. R. Spatiotemporal energy models for the perception of motion. J. Opt. Soc. Am. A 2, 284–299 (1985).
Jagadeesh, B., Wheat, H. S. & Ferster, D. Linearity of summation of synaptic potentials underlying direction selectivity in simple cells of the cat visual cortex. Science 262, 1901–1904 (1993).
van Santen, J. P. & Sperling, G. Elaborated Reichardt detectors. J. Opt. Soc. Am. A 2, 300–321 (1985).
Dror, R. O., O’Carroll, D. C. & Laughlin, S. B. Accuracy of velocity estimation by Reichardt correlators. J. Opt. Soc. Am. A Opt. Image Sci. Vis 18, 241–252 (2001).
Torre, V. & Poggio, T. Synaptic mechanism possibly underlying directional selectivity to motion. Proc. R. Soc. Ser. B Biol. Sci. https://doi.org/10.1098/rspb.1978.0075 (1978).
DeAngelis, G. C., Ohzawa, I. & Freeman, R. D. Receptive-field dynamics in the central visual pathways. Trends Neurosci. 18, 451–458 (1995).
Serbe, E., Meier, M., Leonhardt, A. & Borst, A. Comprehensive characterization of the major presynaptic elements to the Drosophila OFF motion detector. Neuron 89, 829–841 (2016).
Shinomiya, K. et al. Candidate neural substrates for off-edge motion detection in Drosophila. Curr. Biol 24, 1062–1070 (2014).
Fitzgerald, J. E. & Clark, D. A. Nonlinear circuits for naturalistic visual motion estimation. eLife 4, e09123 (2015).
Leonhardt, A. et al. Asymmetry of Drosophila ON and OFF motion detectors enhances real-world velocity estimation. Nat. Neurosci. 19, 706–715 (2016).
Aso, Y. et al. The neuronal architecture of the mushroom body provides a logic for associative learning. eLife 3, e04577 (2014).
Nern, A., Pfeiffer, B. D. & Rubin, G. M. Optimized tools for multicolor stochastic labeling reveal diverse stereotyped cell arrangements in the fly visual system. Proc. Natl. Acad. Sci. USA 112, E2967–E2976 (2015).
Peng, H., Ruan, Z., Long, F., Simpson, J. H. & Myers, E. W. V3D enables real-time 3D visualization and quantitative analysis of large-scale biological image data sets. Nat. Biotechnol. 28, 348–353 (2010).
Pfeiffer, B. D., Truman, J. W. & Rubin, G. M. Using translational enhancers to increase transgene expression in Drosophila. Proc. Natl. Acad. Sci. USA 109, 6626–6631 (2012).
Demerec, M. Biology of Drosophila (Hafner Press, New York, 1965).
Wilson, R. I. & Laurent, G. Role of GABAergic inhibition in shaping odor-evoked spatiotemporal patterns in the Drosophila antennal lobe. J. Neurosci. 25, 9069–9079 (2005).
Edelstein, A. D. et al. Advanced methods of microscope control using μManager software. J. Biol. Methods https://doi.org/10.14440/jbm.2014.36 (2014).
Reiser, M. B. & Dickinson, M. H. A modular display system for insect behavioral neuroscience. J. Neurosci. Methods 167, 127–139 (2008).
Bahl, A., Serbe, E., Meier, M., Ammer, G. & Borst, A. Neural mechanisms for Drosophila contrast vision. Neuron 88, 1240–1252 (2015).
Turner-Evans, D. et al. Angular velocity integration in a fly heading circuit. eLife 6, e23496 (2017).
Tuthill, J. C., Nern, A., Rubin, G. M. & Reiser, M. B. Wide-field feedback neurons dynamically tune early visual processing. Neuron 82, 887–895 (2014).
Takemura, S. Y. et al. Synaptic circuits and their variations within different columns in the visual system of Drosophila. Proc. Natl. Acad. Sci. USA 112, 13711–13716 (2015).
Parag, T., Chakraborty, A., Plaza, S. & Scheffer, L. A context-aware delayed agglomeration framework for electron microscopy segmentation. PLoS One 10, e0125825 (2015).
Cuntz, H., Forstner, F., Borst, A. & Häusser, M. One rule to grow them all: a general theory of neuronal branching and its practical application. PLOS Comput. Biol. 6, e1000877 (2010).
Acknowledgements
We thank A. Nern for providing the driver line and image, K. Shinomiya and Janelia’s FlyEM project team for providing the reconstructed T4 cell morphology, M. Cembrowski for assistance with the NEURON simulations and E. Rogers for help with fly husbandry. We are also grateful to A. Hermundstad, J. Dudman, N. Spruston, B. Mensh and members of the Reiser lab for comments on the manuscript. This project was supported by the Howard Hughes Medical Institute.
Author information
Authors and Affiliations
Contributions
E.G. and M.B.R. designed experiments; E.G. performed experiments and analysis. E.G. and S.R. conducted the simulation study. E.G. and M.B.R. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Integrated supplementary information
Supplementary Figure 1 Mapping T4 Receptive Field center.
(a) Top: expression pattern of the driver line used to target T4 cells (SS02344; reoriented substack of a confocal image volume). Similar images were obtained from at least 5 samples. Bottom: schematic of experimental setup. Blue square represents the full mapping stimulus grid from c. (b) Example single cell responses to ON square flashes (~11° × ~11°), presented for 140ms at each location on the indicated stimulus grid (inset). Individual trials in gray (n = 3 trials), mean in red. Inset: stimulus grid of non-overlapping squares, subtending 78.75° × 67.5° of the visual space. (c) Responses from example cell in b to bright and dark square flashes (n = 3 trials each). Note stimulus grid contains overlapping positions to map RF center more precisely. Inset: stimulus grid highlighting two of the nine stimulus positions with darker squares. This mapping procedure was performed for all the cells in the dataset.
Supplementary Figure 2 Dynamic characterization of the moving bar responses.
(a) Circular mean of preferred direction for all recorded neurons (n = 17 cells). Lines connect data from the same cell, dot color depicts different speeds, and dot size the normalized mean response vector magnitude (scale in inset). (b) Histogram of the data in a, showing three distinct peaks corresponding to three of the four cardinal directions. (c) Responses from an example cell to eight different directions (rows) at four different speeds (columns). Responses were temporally aligned to the time the bar crossed the RF center. (d,e) Mean normalized vector calculated for each time point for responses in c, decomposed into magnitude (d) and angle (e). Vector was calculated from temporally aligned responses presented in c. This procedure can be considered as mimicking a downstream cell’s readout of differently tuned T4 cells with RFs centered at the same spatial position. Note, that for the two slower speeds the instantaneous PD flips by 180° after the bar passes the center (seen clearly in 10 out of 17 cells), since PD response is now hyperpolarizing while ND response is depolarizing (denoted with gray lines).
Supplementary Figure 3 Peak depolarization/hyperpolarization of T4 receptive field.
(a) Normalized peak depolarization (red) and peak hyperpolarization (blue) for all recorded neurons. Here, PD is presented from left to right, with peak depolarization aligned to position zero. A value of 4 indicates that a particular position gave the strongest depolarizing response at all four speeds, and a 2 indicates the largest hyperpolarizing response (since only the two slowest speeds were considered). (b) Angular distance between peaks of the hyperpolarization and depolarization curves in a. Black line indicates the mean.
Supplementary Figure 4 T4 responses to two-step apparent motion show null direction suppression, but no preferred direction enhancement.
Averaged baseline-subtracted responses (mean ± s.e.m.) to 160 ms flash stimuli presented along the PD-ND axis (n = 17 cells; expanded version of stimulus protocol shown in Fig. 3, applied to all recorded T4 neurons, here the five positions sampled are shifted by one position towards the leading side). Stimulus positions indicated correspond to those in Fig. 2. Apparent motion is presented as two flash stimuli timed to match their appearance during 14°/sec motion. PD motion indicated in red and ND motion in blue. Single position responses are shown in gray along the diagonal. Gray traces above and below the diagonal are time-aligned sums (computed as the superposition) of the diagonal SPFRs. Note that no enhancement for second bar responses occurs in the lower triangle, but clear suppression is present for most responses in the upper triangle.
Supplementary Figure 5 Removing features of the SPFRs eliminates directional selectivity.
(a) Comparison of PD and ND responses (mean ± s.e.m. , n = 31 trials, 16 cells) for measured, summed, rectified (summed after hyperpolarization removal), and scaled (rectified and central position response scaled to the magnitude of each position) traces. Data presented as measured and summed is reproduced from Fig. 4d. (b) Boxplots for Directional Selectivity Index (DSI) for the same data as in a by manipulation and speed, gray crosses represent outliers (* indicates DSI > 0 with p < 0.01, one sided unpaired t-test). The response reconstructed from amplitude-scaled versions of the SPFR at the central position (which lack the temporal sharpening of the depolarized component of trailing-edge SPFRs) do not show directional selectivity (see Methods for boxplot conventions). (c) Schematic for procedures applied in rectified and scaled versions of the SPFR sums in a.
Supplementary Figure 6 Detailed simulation results.
(a) Summary of 1000 independent nonlinear least squares fits of simulation parameters (from randomized initial conditions) optimized to reproduce the measured SPFRs. Plot of sorted sum of squared errors (SSE) between each optimization result and the original SPFRs summed over all positions and all speeds. The smallest error solutions are found in distinct clusters that are color-coded and are further examined in b and c. (b) Spatial and temporal filters for excitatory and inhibitory conductances. Top: normalized conductance weights for excitatory (thicker line) and inhibitory synapses in three optimization solution-clusters. Each subplot shows resulting Gaussian distribution from 10, nearly indistinguishable, solutions (chosen at random) from each solution-cluster. Gaussian amplitudes were scaled by RM (inverse of the leak conductance), and the excitatory amplitude was further scaled by 10 for comparison. In solutions 1 and 2, the excitatory distribution is broader, and shifted towards the leading side (0 marks the leading end of the dendrite). Bottom: excitatory and inhibitory conductance pulse for 160 ms flash. In solutions 1 and 2 the excitatory conductance is much faster. Figure 5 data is based on Solution 1, example parameter values in Supplementary Table 1. (c) Comparison of measured SPFR data used for fitting and the simulation results. Only 160ms flashes are shown, but the model was fit to SPFRs at all 4 speeds. Each row shows a single solution from each solution-cluster labeled in a. The 3rd solution does not account for hyperpolarization on the trailing side and was therefore excluded from further analysis. (d) Comparison of mean measured responses to simulated predictions with parameters from solution-cluster 2 (Supplementary Table 1) to moving bars in the PD and ND. (e) Peak PD and ND responses measured in T4s, compared to the solution-cluster 2 simulation results from d. (f) DSI for the mean measured responses compared to the simulation results from d. Note that Fig. 5 b,c,d show these comparisons using solution 1 parameters.
Supplementary Figure 7 The voltage to calcium transformation may produce enhancement artifacts.
(a) Averaged baseline-subtracted responses (mean ± s.e.m.) to 40 ms flash stimuli presented along the PD-ND axis (n = 3, same cells as in Fig. 3) in black. Single position responses are shown along the diagonal. Stimulus positions indicated correspond to those in Fig. 2. The time-aligned sum of the single position responses is shown in gray. Lines demarcate the maximal response to second bar in 3 example positions. Arrows point from summed prediction to measured response. (b) As a proxy for possible effect of calcium imaging21, the same data as in a are plotted after squaring the measured responses (in green). Gray traces represent the sum of squared single position responses. Note that in example i, the slight suppression in a, becomes an enhanced response in b, in example ii minimal enhancement becomes strong enhancement, and in example iii suppression is maintained.
Supplementary Figure 8 The space-time tilt in the T4 spatiotemporal receptive fields likely originates from the interaction of excitatory and inhibitory inputs.
Left: SPFRs from Fig. 2 a (for 160 ms flashes) were replotted to approximate the spatiotemporal RF of T4 cells. Dashed line indicates stimulus onset. The RF features an excitatory lobe peaking in the center (by construction) and an inhibitory lobe following in time and offset spatially towards the trailing side. In this representation, the leading side responses appear to rise more slowly than central responses, which could conform with the temporal delay requirement of an HR-like mechanism. Center: the spatiotemporal RF plotted from simulated SPFRs generated from the (Solution 1) model parameters. Lines correspond to response traces shown in the inset. The apparent difference in onset times for different positions is the result of different response magnitudes, since the time constants at different positions in the model are identical by construction. Right: similar to center, but from simulations where the inhibitory inputs were removed. Note that in the model, removing inhibition completely removes the inseparable property of the filter, showing that the contribution of inhibition is sufficient to account for the tilt in the excitatory lobe.
Supplementary information
Supplementary Text and Figures
Supplementary Figures 1–8
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gruntman, E., Romani, S. & Reiser, M.B. Simple integration of fast excitation and offset, delayed inhibition computes directional selectivity in Drosophila . Nat Neurosci 21, 250–257 (2018). https://doi.org/10.1038/s41593-017-0046-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41593-017-0046-4
This article is cited by
-
Connectome-constrained networks predict neural activity across the fly visual system
Nature (2024)
-
A biophysical account of multiplication by a single neuron
Nature (2022)
-
The physiological basis for contrast opponency in motion computation in Drosophila
Nature Communications (2021)
-
How fly neurons compute the direction of visual motion
Journal of Comparative Physiology A (2020)
-
Elementary motion sequence detectors in whisker somatosensory cortex
Nature Neuroscience (2019)