Abstract
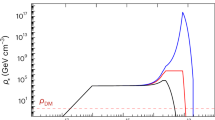
The total mass density of the Universe appears to be dominated by dark matter. However, beyond its gravitational interactions at the galactic scale, little is known about its nature1. Several proposals have been advanced in recent years for the detection of dark matter2–4. In particular, a network of atomic clocks could be used to search for transient indicators of hypothetical dark matter5 in the form of stable topological defects; for example, monopoles, strings or domain walls6. The clocks become desynchronized when a dark-matter object sweeps through the network. This pioneering approach5 requires a comparison between at least two distant optical atomic clocks7–9. Here, by exploiting differences in the susceptibilities of the atoms and the cavity to the fine-structure constant10,11, we show that a single optical atomic clock12 is already sensitive to dark-matter events. This implies that existing optical atomic clocks13,14 can serve as a global topological-defect dark-matter observatory, without any further developments in experimental apparatus or the need for long phase-noise-compensated optical-fibre links15. Using optical atomic clocks, we explored a new dimension of astrophysical observations by constraining the strength of atomic coupling to hypothetical dark-matter cosmic objects. Under the conditions of our experiments, the degree of constraint was found to exceed the previously reported limits16 by more than three orders of magnitude.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Feng, J. L. Dark matter candidates from particle physics and methods of detection. Ann. Rev. Astron. Astrophys. 48, 495–545 (2010).
Budker, D., Graham, P. W., Ledbetter, M., Rajendran, S. & Sushkov, A. O. Proposal for a cosmic axion spin precession experiment (CASPEr). Phys. Rev. X 4, 021030 (2014).
Stadnik, Y. V. & Flambaum, V. V. Searching for topological defect dark matter via nongravitational signatures. Phys. Rev. Lett. 113, 151301 (2014).
Hees, A., Guéna, J., Abgrall, M., Bize, S. & Wolf, P. Searching for an oscillating massive scalar field as a dark matter candidate using atomic hyperfine frequency comparisons. Phys. Rev. Lett. 117, 061301 (2016).
Derevianko, A. & Pospelov, M. Hunting for topological dark matter with atomic clocks. Nat. Phys. 10, 933–936 (2014).
Vilenkin, A. Cosmic strings and domain walls. Phys. Rep. 121, 263–315 (1985).
Rosenband, T. et al. Frequency ratio of Al+ and Hg+ single-ion optical clocks; metrology at the 17th decimal place. Science 319, 1808–1812 (2008).
Le Targat, R. et al. Experimental realization of an optical second with strontium lattice clocks. Nat. Commun. 4, 2109 (2013).
Nemitz, N. et al. Frequency ratio of Yb and Sr clocks with 5 × 10−17 uncertainty at 150 seconds averaging time. Nat. Photon. 10, 258–261 (2016).
Stadnik, Y. V. & Flambaum, V. V. Searching for dark matter and variation of fundamental constants with laser and maser interferometry. Phys. Rev. Lett. 114, 161301 (2015).
Stadnik, Y. V. & Flambaum, V. V. Enhanced effects of variation of the fundamental constants in laser interferometers and application to dark-matter detection. Phys. Rev. A 93, 063630 (2016).
Ludlow, A. D., Boyd, M. M., Ye, J., Peik, E. & Schmidt, P. O. Optical atomic clocks. Rev. Mod. Phys. 87, 637–701 (2015).
Nicholson, T. et al. Systematic evaluation of an atomic clock at 2 × 10−18 total uncertainty. Nat. Commun. 6, 6896 (2015).
Huntemann, N., Sanner, C., Lipphardt, B., Tamm, C. & Peik, E. Single-ion atomic clock with 3 × 10−18 systematic uncertainty. Phys. Rev. Lett. 116, 063001(2016).
Calonico, D., Inguscio, M. & Levi, F. Light and the distribution of time. EPL-Europhys. Lett. 110, 1–11 (2015).
Olive, K. A. & Pospelov, M. Environmental dependence of masses and coupling constants. Phys. Rev. D 77, 043524 (2008).
Stadnik, Y. V. & Flambaum, V. V. Manifestations of dark matter and variations of fundamental constants in atoms and astrophysical phenomena. Preprint at http://arxiv.org/abs/1509.00966 (2015).
Derevianko, A. Atomic clocks and dark-matter signatures. J. Phys. Conf. Ser. 723, 012043 (2016).
Arvanitaki, A., Huang, J. & Van Tilburg, K. Searching for dilaton dark matter with atomic clocks. Phys. Rev. D 91, 015015 (2015).
Abbott, B. P. et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016).
Ade, P. A. R. et al. Detection of B-mode polarization at degree angular scales by BICEP2. Phys. Rev. Lett. 112, 241101 (2014).
Ade, P. A. R. et al. Joint analysis of BICEP2/ Keck Array and Planck data. Phys. Rev. Lett. 114, 101301 (2015).
Bober, M. et al. Strontium optical lattice clocks for practical realization of the metre and secondary representation of the second. Meas. Sci. Technol. 26, 075201 (2015).
Morzyński, P. et al. Absolute measurement of the 1S0–3P0 clock transition in neutral 88Sr over the 330 km-long stabilized fibre optic link. Sci. Rep. 5, 17495 (2015).
Godun, R. M. et al. Frequency ratio of two optical clock transitions in 171Yb+ and constraints on the time variation of fundamental constants. Phys. Rev. Lett. 113, 210801 (2014).
Hinkley, N. et al. An atomic clock with 10−18 instability. Science 341, 1215–1218 (2013).
Al-Masoudi, A., Dörscher, S., Häfner, S., Sterr, U. & Lisdat, C. Noise and instability of an optical lattice clock. Phys. Rev. A 92, 063814 (2015).
Beringer, J. et al. Review of particle physics. Phys. Rev. D 86, 010001 (2012).
Budker, D. & Derevianko, A. A data archive for storing precision measurements. Phy. Today 68, 10 (September, 2015).
Essig, R. et al. Dark sectors and new, light, weakly-coupled particles. Preprint at http://arxiv.org/abs/1311.0029 (2013).
Angstmann, E. J., Dzuba, V. A. & Flambaum, V. V. Relativistic effects in two valence-electron atoms and ions and the search for variation of the fine-structure constant. Phys. Rev. A 70, 014102 (2004).
Flambaum, V. V. & Dzuba, V. A. Search for variation of the fundamental constants in atomic, molecular, and nuclear spectra. Can. J. Phys. 87, 25–33 (2009).
Kessler, T. et al. A sub-40-mHz-linewidth laser based on a silicon single-crystal optical cavity. Nat. Photon. 6, 687–692 (2012).
Pustelny, S. et al. The Global Network of Optical Magnetometers for Exotic physics (GNOME): a novel scheme to search for physics beyond the Standard Model. Ann. Phys.(Berlin) 525, 659–670 (2013).
Pospelov, M. et al. Detecting domain walls of axionlike models using terrestrial experiments. Phys. Rev. Lett. 110, 021803 (2013).
Takamoto, M., Hong, F.-L., Higashi, R. & Katori, H. An optical lattice clock. Nature 435, 321–324 (2005).
Phillips, W. D. & Metcalf, H. Laser deceleration of an atomic beam. Phys. Rev. Lett. 48, 596–599 (1982).
Raab, E. L., Prentiss, M., Cable, A., Chu, S. & Pritchard, D. E. Trapping of neutral sodium atoms with radiation pressure. Phys. Rev. Lett. 59, 2631–2634 (1987).
Morzyński, P. et al. Absolute frequency measurement of rubidium 5S–7S two-photon transitions. Opt. Lett. 38, 4581–4584 (2013).
Acknowledgements
We are grateful to V. V. Flambaum and Y. V. Stadnik for discussions and crucial remarks concerning the response of an atomic clock transition and an optical cavity to variations in the fine-structure constant, which helped us to properly evaluate our constraints. We also thank W. Ubachs and S. Pustelny for the inspiring discussions. The reported measurements were performed at the National Laboratory FAMO in Toruń, Poland, and were supported by a subsidy from the Polish Ministry of Science and Higher Education. Support has also been received from the project, EMPIR 15SIB03 OC18. This project has received funding from the EMPIR programme co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation programme. The individual contributors were partially supported by the National Science Centre of Poland through the following projects: 2015/19/D/ST2/02195, DEC-2013/09/N/ST4/00327, 2012/07/B/ST2/00235, DEC-2013/11/D/ST2/02663, 2015/17/B/ST2/02115 and 2014/15/D/ST2/05281. This research was partially supported by the TEAM Programme of the Foundation for Polish Science, which is co-financed by the EU European Regional Development Fund and the COST Action, CM1405 MOLIM. P.W. is supported by the Foundation for Polish Science’s START Programme.
Author information
Authors and Affiliations
Contributions
P.W. developed the concept, performed the calculations and data analysis, and prepared the manuscript. P.M. and M.B. performed the experiment. M.B., P.M., M.Z., D.L., A.C. and R.C. contributed to the development of the experimental setup. P.W., R.C., M.Z., M.B. and P.M. contributed to the interpretation and discussion of the results. R.C., M.Z., D.L., P.M. and M.B. contributed to the preparation of the manuscript. M.Z. leads the experimental group.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Wcisło, P., Morzyński, P., Bober, M. et al. Experimental constraint on dark matter detection with optical atomic clocks. Nat Astron 1, 0009 (2017). https://doi.org/10.1038/s41550-016-0009
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41550-016-0009
This article is cited by
-
Experimental realization of a 12,000-finesse laser cavity based on a low-noise microstructured mirror
Communications Physics (2023)
-
Quantum networks with neutral atom processing nodes
npj Quantum Information (2023)
-
Resolution of the paradox of the diamagnetic effect on the Kibble coil
Scientific Reports (2021)
-
The local dark sector
Experimental Astronomy (2021)
-
Search for topological defect dark matter with a global network of optical magnetometers
Nature Physics (2021)