Abstract
Electron spins in semiconductors are promising qubits because their long coherence times enable nearly 109 coherent quantum gate operations. However, developing a scalable high-fidelity two-qubit gate remains challenging. Here, we demonstrate an entangling gate between two double-quantum-dot spin qubits in GaAs by using a magnetic field gradient between the two dots in each qubit to suppress decoherence due to charge noise. When the magnetic gradient dominates the voltage-controlled exchange interaction between electrons, qubit coherence times increase by an order of magnitude. Using randomized benchmarking, we measure single-qubit gate fidelities of ~ 99%, and through self-consistent quantum measurement, state, and process tomography, we measure an entangling gate fidelity of 90%. In the future, operating double quantum dot spin qubits with large gradients in nuclear-spin-free materials, such as Si, should enable a two-qubit gate fidelity surpassing the threshold for fault-tolerant quantum information processing.
Similar content being viewed by others
Introduction
The quantum phase coherence of isolated spins in semiconductors1,2,3,4,5,6,7 can persist for long times, reaching tens of milliseconds for electron spins8 and tens of minutes for nuclear spins.9 Such long coherence times enable single-qubit gate fidelities exceeding the threshold for fault-tolerant quantum computing8 and make spins promising qubits. However, entangling spins is difficult because magnetic interactions between spins are weak. For electrons, this challenge can be met by exploiting the charge of the electron for electric-dipole10 or gate-controlled exchange coupling2 between spins. In these methods, however, the qubit energy depends on electric fields, and charge noise in the host material limits single-qubit coherence.11 Charge noise also affects other qubit platforms. For example, heating due to charge noise is a limiting factor in the coherence of trapped ion qubits,12 and the transmon superconducting qubit was designed to suppress noise from charge fluctuations in superconducting islands.13 Strategies such as composite pulses,14, 15 dynamical decoupling,11 and sweet-spot operation16,17,18 have been developed to mitigate the effects of charge noise.
In this work, we present a technique to suppress decoherence caused by charge noise. The key idea is to apply a large transverse qubit energy splitting that does not depend on electric fields and, therefore, suppresses the effects of charge fluctuations. We implement this scheme with two singlet-triplet qubits, each of which consists of two electrons in a double-quantum-dot.2 In each qubit, the voltage-controlled exchange interaction J(ε), where ε represents the gate voltage, splits the singlet \({\left| S\right\rangle } =({\left| \uparrow \downarrow \right\rangle } -{\left| \downarrow \uparrow \right\rangle })/\sqrt{2}\) and triplet \(\left|{T}_{0}\right\rangle =(\left|\uparrow \downarrow \right\rangle +\left|\downarrow \uparrow \right\rangle)/\sqrt{2}\) states in energy,2 where the left (right) arrow indicates the spin of the left (right) electron. A magnetic gradient ΔB Z between the two dots lifts the degeneracy between |↑↓〉 and |↓↑〉. These two mechanisms enable universal quantum control of singlet-triplet qubits.19 Until now, two-qubit gates for singlet-triplet qubits have operated with J(ε)≫ΔB Z , and charge noise is the limiting factor in two-qubit gate fidelities.2, 10 However, if ΔB Z ≫J(ε), the total qubit energy splitting is \(\Omega (\varepsilon)=\sqrt{\Delta {B}_{z}^{2}+J{(\varepsilon)}^{2}}\approx \Delta {B}_{z}+J{(\varepsilon)}^{2}/2\Delta {B}_{z}\), and the qubit sensitivity to charge noise \(\Omega ^{\prime} (\varepsilon) = ({J(\varepsilon)}/{\Delta {B}_{z}}) J^{\prime}\!(\varepsilon)\) is reduced by a factor of J(ε)/ΔB Z , effectively mitigating decoherence due to charge noise.
Intense magnetic field gradients in spin qubits can be created with micromagnets.6, 20, 21 In GaAs quantum dots, strong magnetic gradients can also be generated via the hyperfine interaction between the electron and Ga and As nuclear spins in the semiconductor.19, 22,23,24 Coherence times for qubit rotations around hyperfine gradients can approach one millisecond,25 which is significantly longer than typical exchange coherence times.11 Here, we show that when the magnetic gradient in a GaAs singlet-triplet qubit dominates the electrically controlled exchange interaction, coherence times increase by an order of magnitude. Through both standard and interleaved randomized benchmarking, we measure average single-qubit gate fidelities of ~ 99%. At the same time, this approach maintains a large interaction between adjacent capacitively coupled qubits. We use self-consistent two-qubit state- and measurement tomography to measure a Bell state with a maximum fidelity of 93%. Full process tomography involving 256 tomographic measurements of the two-qubit operation yields an entangling gate fidelity of 90%, consistent with theoretical simulations. In materials without nuclear spins such as silicon, even higher gate fidelities should be possible.
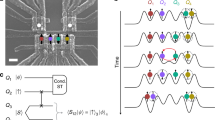
We use two singlet-triplet qubits,2 created in gate-defined double quantum dots similar to those of refs (10, 11) in a GaAs/AlGaAs heterostructure (Fig. 1a). Each double quantum dot contains two electrons. The Hamiltonian for each qubit is H(ε)=J(ε)σ z+ΔB z σ x, in the {|S〉,|T 0〉} basis. J(ε), the exchange interaction between the two spins, depends on ε, the difference in electrochemical potential between the dots (Fig. 1b). ΔB z, the difference in longitudinal magnetic field between the two dots, results from the wavefunction overlap between each electron and the Ga and As nuclear spins in the heterostructure. Although the nuclear spins are unpolarized in thermal equilibrium, ΔB z can be measured and stabilized up to several hundred mT using feedback.19, 22, 23
Experimental set-up. a Scanning electron micrograph of a two-qubit device identical to the one used in this work. Red circles indicate approximate positions of electrons in the double-well potentials created by metal depletion gates (gray). Arrows indicate the positions of sensor quantum dots. A voltage difference ε applied to plunger gates adjusts the exchange interaction. b The gate-contolled wavefunction overlap between electron spins produces the exchange interaction J(ε). Each electron also interacts with a large number of Ga and As nuclear spins (green and orange circles) via the hyperfine interaction, leading to a difference in the longitudinal magnetic gradient between the dots ΔB z = B z,L −B z,R . c Energy level diagram showing the two-electron spin states of a double quantum dot. We operate the qubit with ε < 0 and J(ε)≪ΔB z, as indicated with the dashed gray box. d Calculated qubit energy splitting J(ε) for the two cases when ΔB z = 0 and ΔB z≈1 GHz. When ΔB z is large, the qubit splitting does not depend on ε and is insensitive to electric fields
The two adjacent qubits are capacitively coupled, and the interaction Hamiltonian H int =J 12 σ z ⊗σ z , where \({J}_{12}\propto {J^\prime_1}({\varepsilon }_{1}){J^\prime_2}({\varepsilon }_{2})\),10, 26 and the subscripts refer to the different qubits. For the values of ε used here, we empirically find that J′(ε)∝J(ε). This requires that J(ε) > 0 to maintain nonzero interqubit coupling.
Figure 1c shows the energy level diagram of the two-electron spin states in a double quantum dot. The qubit states are the |S〉 and |T 0〉 levels in the regime where ΔB z≫J(ε) (Fig. 1c, d). Through dynamic nuclear polarization and feedback, we set g * μ B ΔB z/h≈1 GHz in all experiments.19, 22 Here, g * = −0.44 is the effective electron g-factor in GaAs, μ B is the Bohr magneton, and h is Planck’s constant. ΔB z is stabilized to within 3 MHz, corresponding to an inhomogeneously broadened coherence time \({T}_{2}^{\ast }\approx 100\) ns. We initialize the |0〉 state through electron exchange with the leads when ε≫0, where |S〉 is the ground state of the double dot. Then we adiabatically ramp to ε = ε 0 < 0, where 100 MHz<J(ε 0)/2π<300 MHz<ΔB z . We measure the qubit state via electron exchange with the leads in a new technique (see Supplementary Information), which is compatible with large magnetic gradients.27
We drive qubit rotations by adding an oscillating voltage to the plunger gates, such that the total voltage ε(t)=ε 0+ε 1 cos(Ωt). For ε 1≪ε 0, J(t)≈J(ε 0)+2j cos(Ωt), where \(j=\frac{ {\varepsilon}_{1}} {2} J^{\prime} ({\varepsilon }_{0})\) is the Rabi frequency. When the oscillation frequency matches the total qubit splitting \(\Omega =\sqrt{\Delta {B}_{z}^{2}+{J}^{2}({\varepsilon }_{0})}\), the time varying component of J(t) drives qubit transitions (Fig. 2a).23 In this regime, ΔB z is analogous to the external magnetic field for a single spin-1/2, while the time varying component of J(t) is analogous to a perpendicular oscillating magnetic field, which drives transitions. We emphasize that when ΔB z ≫J(ε 0), \(\Omega ({\varepsilon }_{0})\approx \Delta {B}_{z}+\frac{J{({\varepsilon }_{0})}^{2}}{2\Delta {B}_{z}}\), and the sensitivity to charge noise \(\Omega ^{\prime} ({\varepsilon }_{0})=\frac{J({\varepsilon }_{0})}{\Delta {B}_{z}}J^{\prime} ({\varepsilon }_{0})\) is smaller by a factor of \(\frac{J({\varepsilon }_{0})}{\Delta {B}_{z}}\) compared to the case where ΔB z ≪ J(ε 0) (Fig. 1d). However, a key requirement of this technique is that J(ε 0) > 0, in order to maintain J′(ε 0) > 0 for single-qubit control and two-qubit coupling.
Single-qubit operations. a Time-varying voltage pulses resonant with the qubit splitting induce Rabi oscillations. b Coherence times of driven Rabi oscillations (blue) and rotary echo (red) vs. Rabi drive strength. The solid blue line is a theoretical curve taking into account the measured charge and hyperfine noise levels in our qubit. The data agree with the model. The dashed red line between data points is a guide to the eye. At low drive strengths, hyperfine fluctuations limit the coherence time, and at large drive strengths, charge-noise-induced fluctuations in the Rabi frequency limit the coherence. c Randomized benchmarking yields an average gate fidelity of 98.6 ± 0.2%. Error bars are statistical uncertainties. Note that the qubit splitting points along the x direction, and all gates are performed with phase-modulated rf pulses. See Supplementary Information for more details on randomized benchmarking
Large magnetic gradients can, therefore, completely suppress dephasing due to charge noise, although relaxation caused by charge noise at the qubit frequency ΔB z still limits the coherence. In our case, however, nuclear spin noise causes the magnetic gradient to fluctuate. To suppress the effects of hyperfine fluctuations, we apply a strong rf drive to the qubit, causing Rabi oscillations. In the reference frame rotating around the qubit splitting σ x , the Hamiltonian is H rot=jσ z +δΩσ x , where j is the Rabi frequency, and δΩ is a fluctuation in the magnetic gradient. When j≫δ, the qubit splitting in the rotating frame \({\Omega }_{{\rm{rot}}}\approx j+\frac{\delta {\Omega }^{2}}{2j}\) is first-order insensitive to fluctuations in the magnetic gradient.
Results
Figure 2b shows the coherence time of driven Rabi oscillations as a function of drive strength for J(ε 0)/(2π)=220 MHz. The maximum coherence time (≈700 ns) is an order of magnitude larger than that for oscillations around a static exchange splitting with the same J(ε 0) (≈80 ns). However, the quality factor of Rabi oscillations is the same as for static exchange oscillations,11 because low-frequency charge noise limits the coherence time in both cases. But because j≪J(ε 0), the Rabi coherence time is much longer. It is this improvement in coherence that allows increased two-qubit gate fidelities, as described below. Reversing the phase of the drive halfway through the evolution to perform a rotary echo extends the coherence time by an additional factor of 10 (Fig. 2b). Rotating-frame echo coherence times are also an order of magnitude longer than static exchange echo11 dephasing times measured in this device. We do not observe a large increase in coherence with multi-pulse dynamical decoupling, perhaps due to high-frequency charge noise.11
As the amplitude of the oscillating voltage ε 1 increases, both the Rabi and echo coherence times reach a maximum (Fig. 2b). At low drive strengths, hyperfine fluctuations in the detuning limit the coherence. At large drive strengths, charge-noise-induced fluctuations in J′(ε), which cause the Rabi rates to fluctuate in time, limit the coherence. The observed behavior agrees well with a theoretical simulation based on measured noise levels in our qubit (Fig. 2b) (see Supplementary Information). The simulation correctly predicts the maximum coherence time and corresponding Rabi frequency. Using randomized benchmarking,28,29,30,31,32,33,34 we find an average gate fidelity of 98.6 ± 0.2%, with individual gate fidelities close to the average (Fig. 2c). (See the Supplementary Information for further experimental details on randomized benchmarking). Gate fidelities are likely coherence limited as a result of slow electric-field or hyperfine fluctuations. Given the observed quality factor of Rabi oscillations, which is ~ 5, (Fig. 2a), we would expect roughly 10 coherent π rotations within the coherence time. Assuming Gaussian decay due to low-frequency noise, the fidelity of a π-gate should be approximately \({e}^{-{\mathrm{(1/10)}}^{2}}\mathrm{=0.99}\). Because hyperfine or charge fluctuations are slow compared with gate times (≈20 ns), errors are likely correlated,35 as is the case for most spin qubits. Suppressed low-frequency charge noise or composite pulses14, 15 would improve gate fidelities.
Next, we take advantage of the long coherence times in the ΔB z -dominated regime to perform a high-fidelity two-qubit entangling gate. In the lab frame, H≈Ω1 σ x ⊗I+Ω2 I⊗σ x +J 12 σ z ⊗σ z , where I is the identity operator. The single-qubit terms in the Hamiltonian do not commute with the interaction term, and the single-qubit rotations cancel the interaction except when Ω1 = Ω2 (see Supplementary Information), in a manner analogous to the Hartmann-Hahn condition for nuclear double resonance.36 In this case, the interaction in the rotating frame is
Here \({J}_{12}\propto {J^\prime_1}({\varepsilon }_{1}){J^\prime_2}({\varepsilon }_{2})\) is the interaction energy, and ϕ i is the phase of the rf drive on each qubit. When Ω1 = Ω2 and ϕ 1 = ϕ 2, the single-qubit rotations constructively interfere, and the interaction is the same as in the lab frame, up to a factor of 1/2. The order-of-magnitude increase in single-qubit coherence discussed above, therefore, enables a substantially improved two-qubit gate fidelity. This interaction generates an operation equivalent to a controlled phase gate up to single-qubit rotations.
To entangle the qubits, we set Ω1 = Ω2 = 960 MHz and perform a simultaneous rotary echo for varying lengths of time (Fig. 3a), choosing the drive amplitude that maximizes the echo coherence time. Self-consistent two-qubit measurement and state tomography37 (see Supplementary Information) reveal an oscillating concurrence of the two-qubit state (Fig. 3c). The concurrence is defined as C=λ 4−λ 3−λ 2−λ 1, where the λ i are eigenvalues of the two-qubit density matrix, arranged from smallest to largest.38 The concurrence ranges from 1 to −0.5. A value of 0 indicates no entanglement between the qubits, a value of 1 indicates maximal entanglement, and a value of −0.5 indicates complete dephasing. The observed concurrence periodically reaches values above zero, demonstrating repeated entangling and disentangling of the qubits as the interaction time increases. Eventually, the concurrence saturates at a negative value, because both qubits have dephased. We have performed numerical simulations taking into account hyperfine noise and both low- and high-frequency charge noise (see Supplementary Information). The measured concurrence agrees with the simulation (Fig. 3c). As the concurrence reaches a local maximum, the length of the single-qubit Bloch vectors, \(l=\sqrt{{\langle {\sigma }_{x}\rangle }^{2}+{\langle {\sigma }_{y}\rangle }^{2}+{\langle {\sigma }_{z}\rangle }^{2}}\), where \(\langle \cdots \rangle\) indicates a single-qubit expectation value, approach zero, as expected for entangled states (Fig. 3d).
Entangling gate. a To entangle the qubits, we perform a simultaneous rotary echo on both for a varying total length of time t, followed by tomographic readout to reconstruct the two-qubit density matrix. b Bloch vector length for qubit 1, l 1, during the entangling gate as the phase between rf drives varies. Nodes in l 1 denote entanglement. The entanglement rate vanishes when the qubits are driven 90° out of phase. c Concurrence vs. time for the entangling gate. Positive values of concurrence indicate entangled states. Negative values of concurrence indicate decoherence. The solid red line is a theoretical simulation taking into account hyperfine and low- and high-frequency charge noise (see Supplementary Information). d Single-qubit Bloch vector lengths l 1 and l 2 during joint evolution. When the qubits are detuned from each other, the interaction vanishes
As equation (1) suggests, the interaction strength depends on the relative phase between the rf drives on each qubit. We demonstrate phase control of the two-qubit interaction by measuring the length of the Bloch vector of one qubit as we vary the relative phase between qubits (Fig. 3b). As expected, the entangling rate reaches a maximum when the two qubits are driven in phase, and the entangling rate vanishes when the two qubits are out of phase.
The two-qubit interaction also vanishes if Ω1≠Ω2. To demonstrate frequency control of the two-qubit gate, we turn off the dynamic nuclear polarization19 on qubit 2, effectively setting Ω2≈0 MHz. However, all gate voltages during the entangling operation remain the same. Measuring the Bloch vector length of qubit 1 as a function of evolution time shows no oscillations, just a smooth decay (Fig. 3d). This indicates that no entanglement takes place, and hence that the interaction vanishes, when the two qubits are detuned from each other.
To assess the gate fidelity, we perform self-consistent quantum process tomography37, 39, 40 on the two-qubit gate (Fig. 4a–d), requiring 256 tomographic measurements of the two-qubit operation. We extract a maximum gate fidelity of 90 ± 1% based on a measured tomographically complete set of input and output states (see Supplementary Information). The extracted process matrix χ has a few negative eigenvalues, which may result from partially mixed input states. Using a maximum likelihood estimation process to ensure a completely positive process matrix (see Supplementary Information), we extract a gate fidelity of 87 ± 1%, which is consistent with the fidelity obtained by direct inversion.
Process tomography for the two-qubit entangling gate. a Real component of the measured process matrix. b Imaginary component of the measured process matrix. c Real component of the ideal process matrix. d Imaginary component of the ideal process matrix. e Gate fidelity of the measured process matrix and most-likely completely positive process matrix and two-qubit Bell state fidelity as a function of interaction strength. Error bars are statistical errors
Figure 4e shows the maximum observed gate and Bell state fidelity as a function of interaction strength, which is varied by adjusting J(ε 0) on each qubit. Similar to the case of single qubit coherence times, the gate fidelity drops at low interaction rates due to hyperfine noise. Gate fidelities are also expected to drop at fast interaction times due to charge noise, but we did not perform this experiment because our dynamic nuclear polarization feedback is not stable in this regime. An additional source of error at large interaction strengths is relaxation of the qubit states during initialization due to increased charge noise. We observe a maximum concurrence of 0.86 ± 0.02, corresponding to a Bell state fidelity of 93 ± 1%. Given that the observed Bell state fidelities are equal to or slightly larger than the gate fidelities, it is likely that both decoherence and control errors play a role in overall gate fidelity.
Discussion
The maximum entangled state fidelity presented here represents a reduction in infidelity of about a factor of 4 over the previous entangling gate between singlet-triplet qubits,10 because the effects of charge noise are reduced when the magnetic gradient dominates the exchange interaction. This gate can be improved in the future by narrowing the hyperfine distribution41 through rapid Hamiltonian estimation,23 or by using spin qubits in nuclear-spin-free materials such as Si, where strong gradients can be established with micromagnets. We estimate that with laboratory frame coherence times of 1 μs (instead of ≈100 ns here), rotating frame coherence times could increase by as much as 3–4 times. Longer coherence times such as these suggest that two-qubit gate fidelities exceeding 99%, and fault-tolerant quantum computation using spins, are within reach.
Materials and methods
The two double quantum dots are fabricated on a GaAs/AlGaAs hetereostructure with a two-dimensional electron gas located 91 nm below the surface. The two-dimensional electron gas density n = 1.5 ×1011 cm−2 and mobility μ = 2.5 × 106 cm2 V−1s−1 were measured at T = 4K. Voltages applied to Au/Pd depletion gates define the double-dot potential. The qubits are cooled in a dilution refrigerator to a base temperature of ~ 20 mK. An external magnetic field B = 0.7 T is applied in the plane of the semiconductor surface perpendicular to the axis of the double quantum dots. This orientation of the magnetic field ensures effective dynamic nuclear polarization.24
References
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A. 57, 120–126 (1998).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Kim, D. et al. Quantum control and process tomography of a semiconductor quantum dot hybrid qubit. Nature 511, 70–74 (2014).
Koppens, F. H. L. et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766–771 (2006).
Eng, K. et al. Isotopically enhanced triple-quantum-dot qubit. Sci. Adv. 1, 1500214 (2015).
Pioro-Ladriere, M. et al. Electrically driven single-electron spin resonance in a slanting zeeman field. Nat. Phys. 4, 776–779 (2008).
Muhonen, J. T. et al. Storing quantum information for 30 seconds in a nanoelectronic device. Nat. Nanotechnol. 9, 986–991 (2014).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 9, 981–985 (2014).
Saeedi, K. et al. Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science 342, 830–833 (2013).
Shulman, M. D. et al. Demonstration of entanglement of electrostatically coupled singlet-triplet qubits. Science 336, 202–205 (2012).
Dial, O. E. et al. Charge noise spectroscopy using coherent exchange oscillations in a singlet-triplet qubit. Phys. Rev. Lett. 110, 146804 (2013).
Brownnutt, M., Kumph, M., Rabl, P. & Blatt, R. Ion-trap measurements of electric-field noise near surfaces. Rev. Mod. Phys. 87, 1419–1482 (2015).
Houck, A. A., Koch, J., Devoret, M. H., Girvin, S. M. & Schoelkopf, R. J. Life after charge noise: recent results with transmon qubits. Quantum Inf. Process. 8, 105–115 (2009).
Yang, X.-C. & Wang, X. Noise filtering of composite pulses for singlet-triplet qubits. Sci. Rep. 6, 28996 (2016).
Cerfontaine, P. et al. Feedback-tuned noise-resilient gates for encoded spin qubits. ArXiv e-prints, arXiv, 1606.01897 (2016). [cond-mat.mes-hall].
Bertrand, B. et al. Quantum manipulation of two-electron spin states in isolated double quantum dots. Phys. Rev. Lett. 115, 096801 (2015).
Reed, M. D. et al. Reduced sensitivity to charge noise in semiconductor spin qubits via symmetric operation. Phys. Rev. Lett. 116, 110402 (2016).
Martins, F. et al. Noise suppression using symmetric exchange gates in spin qubits. Phys. Rev. Lett. 116, 116801 (2016).
Foletti, S., Bluhm, H., Mahalu, D., Umansky, V. & Yacoby, A. Universal quantum control of two-electron spin quantum bits using dynamic nuclear polarization. Nat. Phys. 5, 903–908 (2009).
Takeda, K. et al. A fault-tolerant addressable spin qubit in a natural silicon quantum dot. Sci. Advan. 2, 1600694 (2016).
Wu, X. et al. Two-axis control of a singlet-triplet qubit with an integrated micromagnet. Proc. Natl Acad. Sci. 111, 11938–11942 (2014).
Bluhm, H., Foletti, S., Mahalu, D., Umansky, V. & Yacoby, A. Enhancing the coherence of a spin qubit by operating it as a feedback loop that controls its nuclear spin bath. Phys. Rev. Lett. 105, 216803 (2010).
Shulman, M. D. et al. Suppressing qubit dephasing using real-time Hamiltonian estimation. Nat. Commun. 5, 5156 (2014).
Nichol, J. M. et al. Quenching of dynamic nuclear polarization by spin-orbit coupling in gaas quantum dots. Nat. Commun. 6, 7682 (2015).
Malinowski, F. K. et al. Notch filtering the nuclear environment of a spin qubit. ArXiv e-prints, arXiv, 1601.06677 (2016). [cond-mat.mes-hall].
Taylor, J. M. et al. Fault-tolerant architecture for quantum computation using electrically controlled semiconductor spins. Nat. Phys. 1, 177–183 (2005).
Barthel, C. et al. Relaxation and readout visibility of a singlet-triplet qubit in an overhauser field gradient. Phys. Rev. B 85, 035306 (2012).
Knill, E. et al. Randomized benchmarking of quantum gates. Phys. Rev. A. 77, 012307 (2008).
Magesan, E., Gambetta, J. M. & Emerson, J. Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett. 106, 180504 (2011).
Magesan, E. et al. Efficient measurement of quantum gate error by interleaved randomized benchmarking. Phys. Rev. Lett. 109, 080505 (2012).
Magesan, E., Gambetta, J. M. & Emerson, J. Characterizing quantum gates via randomized benchmarking. Phys. Rev. A. 85, 042311 (2012).
Epstein, J. M., Cross, A. W., Magesan, E. & Gambetta, J. M. Investigating the limits of randomized benchmarking protocols. Phys. Rev. A. 89, 062321 (2014).
Muhonen, J. T. et al. Quantifying the quantum gate fidelity of single-atom spin qubits in silicon by randomized benchmarking. J. Phys.: Condens. Matter 27, 154205 (2015).
Kawakami, E. et al. Gate fidelity and coherence of an electron spin in an si/sige quantum dot with micromagnet. Proc. Natl Acad. Sci. 113, 11738–11743 (2016).
Ball, H., Stace, T. M., Flammia, S. T. & Biercuk, M. J. Effect of noise correlations on randomized benchmarking. Phys. Rev. A. 93, 022303 (2016).
Hartmann, S. R. & Hahn, E. L. Nuclear double resonance in the rotating frame. Phys. Rev. 128, 2042–2053 (1962).
Takahashi, M., Bartlett, S. D. & Doherty, A. C. Tomography of a spin qubit in a double quantum dot. Phys. Rev. A. 88, 022120 (2013).
Hill, S. & Wootters, W. K. Entanglement of a pair of quantum bits. Phys. Rev. Lett. 78, 5022–5025 (1997).
Chuang, I. L. & Nielsen, M. A. Prescription for experimental determination of the dynamics of a quantum black box. J. Mod. Opt. 44, 2455–2467 (1997).
Poyatos, J. F., Cirac, J. I. & Zoller, P. Complete characterization of a quantum process: the two-bit quantum gate. Phys. Rev. Lett. 78, 390–393 (1997).
Klauser, D., Coish, W. A. & Loss, D. Nuclear spin state narrowing via gate-controlled rabi oscillations in a double quantum dot. Phys. Rev. B 73, 205302 (2006).
Acknowledgements
We thank Stephen Bartlett and Andrew Doherty for valuable discussions. This research was funded by the United States Department of Defense, the Office of the Director of National Intelligence, Intelligence Advanced Research Projects Activity, and the Army Research Office grant W911NF-11-1-0068. S.P.H. was supported by the Department of Defense through the National Defense Science Engineering Graduate Fellowship Program. This work was performed in part at the Harvard University Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Infrastructure Network (NNIN), which is supported by the National Science Foundation under NSF award No. ECS0335765.
Competing Interests
The authors declare no conflict of interest.
Author information
Authors and Affiliations
Contributions
S.F., G.C.G., and M.J.M. grew and characterized the AlGaAs/GaAs heterostructure. S.P.H. fabricated the device. J.M.N. and L.A.O. performed the experiments. All authors discussed and analyzed the data and wrote the manuscript. A.Y. supervised the project.
Corresponding author
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Nichol, J.M., Orona, L.A., Harvey, S.P. et al. High-fidelity entangling gate for double-quantum-dot spin qubits. npj Quantum Inf 3, 3 (2017). https://doi.org/10.1038/s41534-016-0003-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-016-0003-1
This article is cited by
-
Long-lived valley states in bilayer graphene quantum dots
Nature Physics (2024)
-
Limitations on the maximal level of entanglement of two singlet–triplet qubits in GaAs quantum dots
Quantum Information Processing (2024)
-
Probing two-qubit capacitive interactions beyond bilinear regime using dual Hamiltonian parameter estimations
npj Quantum Information (2023)
-
Scalable and robust quantum computing on qubit arrays with fixed coupling
npj Quantum Information (2023)
-
Wigner-molecularization-enabled dynamic nuclear polarization
Nature Communications (2023)