Introduction

Atrial fibrillation (AF) is one of the most common cardiovascular diseases and has caused considerable economic burden worldwide [1, 2]. Rivaroxaban is an available non-vitamin K antagonist oral anticoagulant (NOAC), which directly inhibits the activity of factor Xa [3]. It has been widely used to prevent stroke in patients with non-valvular atrial fibrillation (NVAF) [4, 5].

Following oral administration, rivaroxaban is rapidly absorbed and reaches the maximum plasma concentration after 2–4 h [6, 7]. For doses greater than 10 mg, taking rivaroxaban with food is necessary to increase bioavailability [8]. Rivaroxaban has a high plasma protein binding (92%–95%) and a mean volume of distribution of 0.62 L/kg [3]. Approximately two-thirds of rivaroxaban is metabolized by the liver, and hepatic cytochrome P450 enzymes (CYP) 3A4/5 account for ~18% of rivaroxaban metabolism [3, 9]. Another one-third of rivaroxaban is eliminated unchanged in the urine, primarily via active renal secretion [3, 9]. P-glycoprotein and breast cancer resistance protein (BCRP), encoded respectively by the ATP-binding cassette sub-family B member (ABCB1) gene and ATP-binding cassette sub-family G member (ABCG2), are the main transporters involved in the process of active renal secretion [9, 10].

Twenty milligrams every 24 h (q24h) as a standard dose for NVAF patients with creatinine clearance (CrCl) ≥50 mL/min and 15 mg q24h for patients with CrCl 30–49 mL/min were recommended by the Food and Drug Administration (FDA) of the United States [9], the National Medical Products Administration (NMPA) of China, as well as “guideline of stroke prevention in Chinese patients with AF” [11]. However, a lower rivaroxaban dose (15 mg for CrCl ≥50 mL/min or 10 mg for CrCl 30–49 mL/min) was approved for Japanese patients by the Pharmaceuticals and Medical Devices Agency of Japan. On the one hand, a higher exposure in Japanese patients was observed compared to Caucasian patients at the same dose [12,13,14,15]. On the other hand, the efficacy and safety of the lower dose for Japanese patients was demonstrated in a phase III clinical trial of J-ROCKET AF compared with the non-Japanese trial of ROCKET AF [12, 16].

Recent studies conducted in Korea and China Taiwan, China demonstrated that a lower rivaroxaban dose was associated with a lower risk of thromboembolic events, intracranial hemorrhage, and all-cause mortality in contrast to those administered warfarin [17,18,19]. Moreover, compared to the standard 15 mg dose, a lower dose of 10 mg was associated with a lower risk of major bleeding in patients with impaired renal function [20, 21]. However, thus far, little is known about the pharmacokinetic-pharmacodynamic (PK-PD) characteristics regarding the optimal dosage of rivaroxaban in Chinese NVAF patients in a real clinical setting.

Therefore, a prospective clinical study was conducted to develop a population PK-PD model of rivaroxaban in Chinese patients with NVAF to (i) evaluate the ethnic differences in PK among Chinese, Caucasian, and Japanese populations; (ii) assess the effect of renal function and other potential variables on the PK and PD of rivaroxaban; and (ii) provide individualized dosing strategies for Chinese patients using the established model.

Materials and methods

Study design

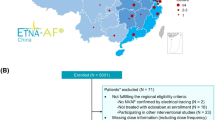
A prospective, single-center clinical study was conducted at Huashan Hospital, Fudan University, China (https://www.chictr.org.cn/index.aspx, ChiCTR2100046685). Patients diagnosed with NVAF using an electrocardiogram according to the 2016 European Heart Rhythm Association Guidelines [22] and receiving rivaroxaban for at least 3 continuous doses were recruited in this study from September 1, 2020, to June 30, 2021. Patients were excluded if they exhibited at least one of the following: (1) moderate or severe liver dysfunction (Child–Pugh classification B or C [23]); (2) severe renal dysfunction (CrCl calculated using the Cockcroft-Gault formula [24] <15 mL/min); (3) pregnancy; (4) history of malignant tumor; or (5) spontaneous bleeding tendency, such as coagulation disorder or thrombocytopenia (blood platelet count <20 × 109/L).

Patient demographics and laboratory test results were collected. Other data collected included the dosing histories of concomitant drugs that inhibit or induce CYP450 3A enzymes and drug transport systems and may change the exposure of rivaroxaban as listed in the FDA label. These drugs included ketoconazole, ritonavir, clarithromycin, erythromycin, carbamazepine, rifampin, St. John’s wort, enoxaparin, warfarin, aspirin, clopidogrel, other platelet aggregation inhibitors, or non-steroidal anti-inflammatory drugs. The rivaroxaban dose amount and dosing time were also recorded for each participant. CHA2DS2-VASc (congestive heart failure, hypertension, age, diabetes, previous stroke/transient ischemic attack, vascular disease, sex category) scores [25] and HAS-BLED (hypertension, abnormal liver/renal function, stroke history, bleeding history or predisposition, labile INR, elderly, drug/alcohol usage) scores [26] were calculated to assess the risk of thromboembolism and bleeding.

Blood samples from inpatients were collected before (defined as trough samples), 3 ± 0.5 h (defined as peak samples) and 7 ± 0.5 h after at least three continuous doses, according to the design of previous studies [14, 27]. Blood samples from outpatients were collected opportunistically. The timing of dosing and sampling was recorded for each patient.

At each sampling, 2.7 mL blood samples were collected into trisodium citrate-containing tubes for measurement of prothrombin time (PT). Another 2 mL of blood was collected into ethylenediaminetetraacetic acid-containing tubes for measurement of rivaroxaban plasma concentration and extraction of genomic DNA. Samples were centrifuged at 3000 × g for 10 min at 20 °C within 4 h of sample collection. All samples were stored at −80 °C and analyzed within 3 months.

This study followed the principles of the Declaration of Helsinki (2013) and was approved by the Ethics Committee of Huashan Hospital (KY2020-016). Informed consent was obtained from all the participants prior to enrollment.

Bioassay

A sensitive ultra-performance liquid chromatography with tandem mass spectrometry method was used to measure the rivaroxaban plasma concentration [28]. The lower limit of quantitation was 1 μg/L, and the calibration range of this assay was 1–1000 μg/L. The inter- and intra-accuracies were 85.9%–114%, and intra- and inter-day precision was less than 10%.

PT was measured with Thromborel® S (Siemens, Marburg, Germany) using a CN6000 coagulation analyzer (Sysmex, Kobe, Japan). The reported range was 0–170 s. The within-run and inter-run precision was <3% [29].

Genotyping

Single nucleotide polymorphisms (SNPs) for four genes involved in the PK of rivaroxaban—ABCB1, ABCG2, CYP3A4, and CYP3A5—were collected from the 1000 Genome Project (https://www.ncbi.nlm.nih.gov/variation/tools/1000genomes/) and the dbSNP database of the National Center for Biothechnology Information (NCBI) (https://www.ncbi.nlm.nih.gov/snp/) and analyzed using Haploview software (version 4.20, https://www.broadinstitute.org/haploview/haploview). Candidate SNPs were included in the analysis according to the following criteria: (i) the minor allele frequency was >20% and (ii) alleles identified by the tests had an r2 threshold of 0.8, as the default in the Haploview software, and have also been commonly used in previous studies [30, 31].

Genomic DNA was extracted using a TIANGEN DNA Kit (DP348, TIANGEN Biotech, Beijing, China) according to the manufacturer’s protocol. Genotypes were analyzed using the MALDI-TOF MassArray assay by Shanghai Benegene Biotechnology Co., Ltd. (Shanghai, China). The exact test for Hardy-Weinberg equilibrium was performed using the HardyWeinberg package (version 1.7.2) in R software (version 4.1.1, R Foundation for Statistical Computing, Vienna, Austria).

Population pharmacokinetic-pharmacodynamic modeling

Population PK-PD analysis was performed using non-linear mixed-effects modeling (NONMEM®, version 7.4.2; ICON Development Solutions, Ellicott City, MD, USA) with first-order conditional estimation with interaction method. The evaluation of the NONMEM output, statistical analysis, and diagnostic plots was performed using R software and Pirana software (version 2.9.7, Certara, Inc., NJ, USA).

Compared to the “gold standard” simultaneous modeling method, a sequential modeling strategy is more time-saving, and estimates are also more likely to be obtained [32, 33]. Therefore, the sequential modeling strategy was first applied to the development of the population PK model, and then individual empirical Bayesian estimates of PK parameters were used as input for the second stage of sequential PD modeling. Finally, a linked population PK-PD model was applied to estimate all PK-PD parameters simultaneously and to compare the parameter estimates via a sequential modeling strategy.

Population pharmacokinetic modeling

Base model

One-compartment and two-compartment models were tested as candidate structural models. The base model including bodyweight with allometric scaling was also tested, according to a previous pooled population PK studies based on 4918 patients [34], as well as classical allometric scaling (0.75 for apparent clearance (CL/F), and 1 for apparent volume of distribution (V/F)) [35], which considered bodyweight as a significant covariate for both CL/F and V/F. The selection of the structural model was based on the Akaike information criterion, Bayesian information criterion, condition number, and precision of estimates. An exponential model for between-subject variability (BSV) was applied to the PK parameters in below equation:

$$P_i = P_{pop}\cdot e^{\eta _i}$$
(1)

where and Pi represents the individual parameter estimate of the ith patient, Ppop represents the typical population parameter estimate, ηi is normally distributed with a mean of zero and variance of ω2.

Residual unexplained variability (RUV) was tested using an additive (Eq. (2)), proportional (Eq. (3)) or combined models (Eq. (4)):

$$Y = IPRED + \varepsilon _1$$
(2)
$$Y = IPRED\cdot (1 + \varepsilon _2)$$
(3)
$$Y = IPRED\cdot \left( {1 + \varepsilon _2} \right) + \varepsilon _1$$
(4)

where Y represents the observation, IPRED represents the individual predicted concentration, and ε1 and ε2 represent the additive and proportional error components, respectively, which are assumed to be normally distributed with a mean of zero and variance of σ2.

Covariate model

Potential covariates were tested, including age, sex, body weight, body surface area, lean body mass, white blood cell count, red blood cell count, hemoglobin (HGB), hematocrit, platelet count, aspartate aminotransferase, alanine aminotransferase, total bilirubin (TBIL), direct bilirubin, alkaline phosphatase, albumin, gamma-glutamyl transpeptidase, urea nitrogen, urea acid, serum creatinine, CrCl, and eGFR (calculated using the Chronic Kidney Disease Epidemiology Collaboration formula [36]). For concomitant drugs, only those with a comedication rate >15% were tested. Continuous covariates were tested using a proportional (Eq. (5)), exponent (Eq. (6)), or power (Eq. (7)) model.

$$P_i = P_{pop}\cdot \left( {1 + \theta \cdot \frac{{COV}}{{COV_{median}}}} \right)$$
(5)
$$P_i = P_{pop}\cdot \left( {\frac{{COV}}{{COV_{median}}}} \right)^\theta$$
(6)
$$P_i = P_{pop}\cdot e^{\theta \cdot (COV - COV_{median})}$$
(7)

where COV and COVmedian represent the individual and median values of a covariate, respectively, θ represents the estimated value of the covariate effect.

Categorical covariates, such as SNPs, were tested using a scale model (Eq. (8)).

$$P_i = \left\{ {\begin{array}{*{20}{c}} {P_{pop}(if\,{\it{homozygous}}\,wild\,type\,carriers)} \\ {P_{pop}\cdot \theta _1(if\,{\it{heterozygous}}\,mutation\,carriers)} \\ {P_{pop}\cdot \theta _2(if\,{\it{homozygous}}\,mutation\,carriers)} \end{array}} \right.$$
(8)

where θ1 and θ2 represent the change of typical values with heterozygous mutation carriers and homozygous mutation carriers compared to homozygous wild-type carriers, respectively. Each SNP was tested individually. Besides, dominant model and recessive model were also tested.

The covariate model was built using a stepwise forward inclusion and backward elimination process. The criteria for covariate selection included a decrease in objective function value (OFV) > 3.84 (df = 1, P < 0.05) in the forward selection step and an increase in OFV > 6.63 (df = 1, P < 0.01) in the backward elimination step. For continuous variables, if PK parameter estimates calculated with the maximum or minimum of the covariate changed less than 20% relative to the population PK estimate, the effect of covariates was not considered clinically relevant. Similarly, if PK parameter estimates in the presence of the categorical variable changed less than 20% relative to the population PK estimate, it was also not clinically relevant. The selection of covariate model also considered the physiological plausibility and goodness-of-fit (GOF) plots.

Population pharmacodynamic modeling

Individual PK parameters were estimated using the POSTHOC method with the established population PK model to develop the population PD model. Structural models were assessed using a linear (Eq. (9)) or near-linear (Eqs. (10, 11)) model, according to previous studies [14, 27, 37].

$$PT = PT_{base} + slope \times C_p$$
(9)
$$PT = PT_{base} + slope \times C_p^{hill}$$
(10)
$$PT = PT_{base} + slope \times C_p^{1 - hill \times C_p}$$
(11)

where PTbase represents the baseline of PT, Cp represents the rivaroxaban plasma concentration, slope represents the change in PT resulting from the change per unit concentration, and hill represents the exponent of Cp.

BSV was tested using an exponential (Eq. (1)) or additive (Eq. (12)) model.

$$P_i = P_{pop} + \eta _i$$
(12)

The RUV was tested using an additive (Eq. (2)), proportional (Eq. (3)) or combined model (Eq. (4)). The method for selection of the structural model, covariate screening, and selection criteria of covariates were the same as those in the development of the population PK model. The effect of SNPs was not tested in the PD model, because they all referred to transporters or drug-metabolizing enzymes in the PK process and had no direct effect on PD.

Model evaluation

The performance of the final model was evaluated using diagnostic GOF plots, including observed values (DV) versus population predicted values (PRED), DV versus individual predicted values (IPRED), conditional weighted residuals (CWRES) versus PRED, and CWRES versus time after last dose.

The robustness of the final model was evaluated using nonparametric bootstrap resampling (n = 2000). The median and 2.5th–97.5th percentiles of parameter estimates from the resampled datasets were calculated and compared with the final parameter estimates.

The visual predictive check (VPC) approach was used to evaluate the predictive performance of the model based on simulations (n = 1000). The median and 5th–95th percentiles of the observed data with the corresponding simulated data were compared. The consistency of variability and the central tendency between the observed and simulated data were visually assessed.

Bootstrap and VPC analyses were performed using Perl-speaks-NONMEM software (PsN, version 4.6.0, Department of Pharmaceutical Biosciences, Uppsala University, Sweden, https://uupharmacometrics.github.io/PsN/index.html).

Model-informed precision dosing

Monte Carlo simulations were employed to compare PK exposure by ethnic groups based on the established population PK model, as well as the reports from a Caucasian NVAF population [27] and Japanese NVAF population [15]. The area under the concentration-time curve over 24 h at steady state (AUC24,ss) was estimated for Caucasian, Japanese and Chinese patients taking 10, 15 or 20 mg q24h, as shown in below equation.

$$AUC_{24,ss} = \frac{{DOSE(mg)}}{{CL/F(L/h)}}$$
(13)

In each model, 1000 simulations were performed based on three typical patients, who had normal, mildly impaired, and moderately impaired renal function, respectively.

Furthermore, simulations were employed based on the final population PK-PD model to evaluate the effect of covariates on the PK and PD of rivaroxaban at various dosing levels. Rivaroxaban concentration-time and PT-time distribution under different dosing strategies to match the exposure of patients at different levels of covariates were simulated to estimate AUC24,ss and average PT at steady state (PTave,ss) for each group (n = 1000). AUC24,ss was calculated using Eq. (13), and PTave,ss was calculated according to its relationship with the average concentration at steady state (Cave,ss), as shown in Eq. (14), where Cave,ss is calculated using Eq. (15).

$$PT_{ave,ss} = f(C_{ave,ss})$$
(14)
$$C_{ave,ss} = AUC_{24,ss}/24$$
(15)

The range of the 5th–95th percentiles of AUC24,ss and PTave,ss for a typical patient was set as the reference range. The optimal dose for patients with different levels of covariates was defined as the dose at which PTave,ss and AUC24,ss falls within the reference range in maximum proportion as estimated from the established PK-PD model.

Results

Study population

Data from 195 patients were collected in this study, with 256 concentration measurements and 244 PT measurements available for PK-PD modeling. Approximately 70% and 17% of the samples were collected before and 3 ± 0.5 h after administration, respectively. Patient demographics are shown in Table 1. The prescribed daily dose ranged from 5 to 20 mg. The eGFR ranged from 22 to 128 mL/min, and 24.6% of the patients had an eGFR of 15–50 mL/min. Median CHA2DS2-VASc score and HAS-BLED score were 2.7 and 2.4, respectively. All participants were administered rivaroxaban with food. None of the investigated medications accounted for >15% of the patients.

Table 1 Baseline patient characteristics.
Full size table

By screening 1000 Genome Project and the dbSNP database of NBCI, identified SNPs included ABCB1 3435 C>T (rs1045642), 1236 C>T (rs1128503), 2677 G>T/A (rs2032582), rs2235035, rs4148738, and rs868755; ABCG2 rs1448784, rs2231137, rs2231142, and rs3114018; CYP3A4 rs2242480, rs2246709, rs3735451, and rs4646440; and CYP3A5*3 (rs776746). Primer sequences for SNPs were shown in Supplementary Table S1. ABCB1 rs2032582 failed the Hardy-Weinberg equilibrium test (P < 0.05); thus, it was excluded from further analysis. Genotype distribution and allele frequencies of the included SNPs are shown in Table 2. The minor allele frequencies of other SNPs were consistent with those reported in the dbSNP database of NCBI.

Table 2 Frequency of distribution of genetic polymorphisms.
Full size table

Population pharmacokinetic-pharmacodynamic model

Population pharmacokinetic model

The PK of rivaroxaban was described by a one-compartment model with first-order absorption and elimination. Allometric scaling factors were not included in the model because they could not be precisely estimated (relative standard error (%RSE) > 130%). Because of the limited samples in the absorption phase, a previously reported ka of 0.617 h−1 was applied in this study [15]. In addition, because the majority of the samples were collected before dosing, the BSV of V/F could not be estimated precisely and thus was removed. Of the tested RUV models, an additive RUV model had the highest OFV; a combined RUV model had a similarly lower OFV with a proportional model, and the additive error of the combined RUV could not be estimated precisely (%RSE=187%). Therefore, a proportional RUV model was adopted for the rivaroxaban concentration.

In the forward inclusion step, eGFR, ABCB1 rs4148738, and CYP3A4 rs2246709 were shown to significantly affect CL/F. In the backward elimination step, the effect of CYP3A4 rs2246709 was removed because of an increase in OFV < 6.63 (Supplementary Table S2). Moreover, the effect of ABCB1 rs4148738 on CL/F was only 19% on CL/F, which was not considered clinically relevant. Therefore, only the effect of the eGFR was retained. The BSV of V/F was not estimated, and no covariates were screened based on V/F. The estimates of the established population PK model parameters are presented in Table 3. The OFV of the final population PK model was 2211.533, with a decrease of 35.058 compared with the base model.

Table 3 Population parameter estimates for the pharmacokinetic-pharmacodynamic model.
Full size table

Population pharmacodynamic model

A linear model (Eq. (9)) described the relationship between rivaroxaban PK and PT, whereas near-linear models as Eqs. (10) and (11) failed to fit the data because of the %RSE of slope or hill > 100%. An exponential BSV model and proportional RUV model were applied to the PT model. In the forward inclusion step, the model with TBIL, eGFR, and HGB was successively detected as having significant covariates for PTbase. In the backward elimination step, HGB was removed by an increase in OFV < 6.63 (P < 0.01) (Supplementary Table S3). The OFV dropped from 582.25 in the base model to 534.86 in the final model. The estimates of the PD model parameters are presented in Table 3.

Population pharmacokinetic-pharmacodynamic model

A simultaneous modeling strategy was successfully applied to fit all the PK and PD data. The estimates of the linked population PK-PD model parameters are listed in Table 3. The difference in parameter estimates between the two modeling strategies was less than 9%. There was a drop in OFV of 85.72 in the final population PK-PD model compared to that in the base model.

The equations for CL/F and PT are as shown in below equations.

$$CL/F(L/h) = 5.03 \times \left( {\frac{{eGFR}}{{80}}} \right)^{0.53}$$
(16)
$$PT = \,13.9 \times e^{0.00574 \times (TBIL - 12)} \times \left[ {1 - 0.0872 \times \left( {\frac{{eGFR}}{{80}}} \right)} \right] \\ + 0.0133 \times C_p$$
(17)

where Cp represents rivaroxaban plasma concentration.

Model evaluation

Diagnostic GOF plots for population PK and PD models are shown in Figs. 1 and 2, respectively. The predicted and observed rivaroxaban plasma concentrations and PT levels showed adequate agreement over the whole range. No obvious bias or trends are shown in scatterplots of CWRES versus time after last dose and CWRES versus PRED.

Fig. 1: Goodness-of-fit plots of the final population pharmacokinetic model.
figure 1

(a) Observed rivaroxaban concentration (DV) versus population predicted concentration (PRED); (b) DV versus individual predicted concentration (IPRED); (c) conditional weighted residuals (CWRES) versus PRED; (d) CWRES versus time after last dose.

Full size image
Fig. 2: Goodness-of-fit plots of the final population pharmacodynamic model.
figure 2

(a) Observed prothrombin time (PT) versus population predicted PT (PRED); (b) observed PT versus individual predicted PT; (c) conditional weighted residuals (CWRES) versus PRED; (d) CWRES versus time after last dose.

Full size image

The robustness of the linked population PK-PD model was evaluated using a nonparametric bootstrap method. The median values from the resampling dataset were within ±3% of the original estimates for all PK-PD parameters, as shown in Table 3.

VPC showed that the median and 95% confidence intervals based on model-based PK-PD predictions were consistent with the observed data (Fig. 3).

Fig. 3: Visual predictive check of the final model.
figure 3

(a) Population pharmacokinetic model; (b) population pharmacodynamic model. Open circles represent the observed data. Red solid lines and blue dashed lines represent the median and 90% confidence intervals, respectively, of observed data. Red shaded areas represent nonparametric 95% confidence intervals of the median values of model-based predictions; blue shaded areas represent nonparametric 95% confidence intervals of the 5th and 95th percentiles of model-based predictions.

Full size image

Model-informed precision dosing

PK exposure in Chinese, Japanese, and Caucasian patients based on the established model as well as previous reports are shown in Fig. 4. For patients with normal renal function (eGFR or CrCl, 80 mL/min) at a 20 mg dose, the AUC24,ss increased by 31% in Chinese patients compared to that in Caucasian patients. When reducing this to a 15 mg dose for Chinese patients, the AUC24,ss was almost comparable with that in Caucasian patients taking 20 mg (Fig. 4a), and the probability of target attainment was ~85%. Compared to that in Chinese patients with normal renal function taking a 15 mg dose, the AUC24,ss in patients with mildly (eGFR or CrCl, 50 mL/min) or moderately (eGFR or CrCl, 30 mL/min) impaired renal function increased by 29% and 73%, respectively (Fig. 4b, c). For Chinese patients with moderately impaired renal function, reducing the dose to 10 mg might lead to values more comparable to the patients with normal renal function.

Fig. 4: Comparison of estimated level of pharmacokinetic exposure.
figure 4

The bold horizontal bars represent the median values of estimated AUC24,ss. The black dashed and dotted lines represent the median and 5th–95th percentiles of the AUC24,ss for Caucasian patients (CrCl ≥ 50 mL/min, taking 20 mg q24h) as reported by Mueck et al. [3]. Typical patients (a) 65 years old, SCr 0.95 mg/dL, eGFR (or CrCl) 80 mL/min, HCT 40.0%; (b) 75 years old, SCr 1.5 mg/dL, eGFR (or CrCl) 50 mL/min, HCT 40.0%; (c) 85 years old, SCr 2 mg/dL, eGFR (or CrCl) 30 mL/min, HCT 40.0%. The gray boxplot in each panel represents the dose regimen with the highest probability of target attainment for Chinese.

Full size image

The 15-mg dose was set as the standard dose for typical patients in the following analysis. The reference population was defined as male patients aged 70 years, body weight 70 kg, eGFR 80 mL/min, TBIL 12 μmol/L, and receiving rivaroxaban 15 mg q24h. The reference range of AUC24,ss (5th–95th percentiles) was 1716–5390 μg·h·L−1, which was similar to the range in Caucasian populations taking 20 mg q24h reported in a previous study (1860–5434 μg·h·L−1) [3]. The reference of PTave,ss (5th–95th percentiles) was 12.9–18.3 s.

When eGFR decreased from 80 mL/min to 50 and 30 mL/min, AUC24,ss increased by ~28.3% and 68.1% at a 15-mg dose, respectively. Patients with eGFR ≥ 50 mL/min may require a dose of 15 mg. For patients with eGFR of 30–49 mL/min, the dose needs to be reduced to 10 mg (Fig. 5a).

Fig. 5: Boxplots of the distribution of simulated area under the concentration-time curve over 24 h and average prothrombin time at steady state based on 7.5, 10, 15, and 20 mg q24h regimens for non-valvular atrial fibrillation patients.
figure 5

The distribution of simulated (a) area under the concentration-time curve over 24 h at steady state (AUC24,ss); (b) average prothrombin time at steady state (PTave,ss). The black dotted lines represent the range of the 5th–95th percentiles of AUC24,ss and PTave,ss for typical patients (70 years, body weight 70 kg, eGFR 80 mL/min, TBIL 12 μmol/L) with 15 mg q24h of rivaroxaban.

Full size image

Compared with that in a patient (eGFR 80 mL/min, TBIL 12 μmol/L) taking 15 mg q24h, the sole effect of increased TBIL or decreased eGFR was less than 20% for most patients. However, for patients with TBIL of 34 μmol/L and eGFR of 30 mL/min, the change in PTave,ss was ~25.5%. The change in PTave,ss could be less than 20% when patients received an adjusted dose based on the eGFR, as previously demonstrated. However, an approximate 18% increase in PTave,ss was still observed for patients with TBIL of 34 μmol/L and eGFR of 30 mL/min, even though the dose was reduced to 10 mg q24h (Fig. 5b).

Discussion

This is the first study to develop a population PK-PD model of rivaroxaban in Chinese patients with NVAF. The established population PK-PD model comprehensively described the effect of eGFR on CL/F as well as the effect of TBIL and eGFR on the baseline of PT. Exposure in Chinese patients receiving 15 mg q24h of rivaroxaban is similar to that in Caucasian patients taking 20 mg q24h. Patients with eGFR of 30–49 mL/min taking 10 mg have a similar exposure to that in patients with eGFR > 50 mL/min taking 15 mg. These findings support lower rivaroxaban doses in Chinese patients than in Caucasian patients. Moreover, the established PK-PD model indicated that there is a high risk of PT overexposure in patients with TBIL ≥ 34 μmol/L and eGFR ≤ 30 mL/min.

The typical value of CL/F in our study was 5.03 L/h, which is similar to the values estimated in Japanese NVAF patients (4.72–4.73 L/h) [14, 15], but was lower than that in Caucasian NVAF patients (6.10 L/h) [27]. The lower CL/F in the Japanese population than in the Caucasian population taking the same dose of rivaroxaban, which led to higher exposure, can be partly explained by the higher proportion of older age and lower body mass in Japanese patients [14, 15, 38]. These two clinical variables (age and weight) were also reported as significant covariates for CL/F in a previous population PK model [34]. A similar estimate of typical CL/F was observed between Chinese patients and Japanese patients, and it also may be attributed to the similar demographic characteristics of the two populations (age, 68 versus 72 years; body weight, 68 versus 64 kg; serum creatinine, 0.92 versus 0.9 mg/dL).

Previous studies had investigated the PK and PD of rivaroxaban in healthy Chinese subjects [39, 40]. No studies had been performed to explore the PK and PD of rivaroxaban in NVAF patients with or without renal and hepatic impairment and to assess the rationality of dose regimens. Based on the Monte Carlo simulation, Chinese patients taking 20 mg q24h of rivaroxaban experienced an increase in AUC24,ss compared to that in Caucasian patients, whereas 15 mg q24h of rivaroxaban yielded a similar exposure to that in Caucasian patients. Due to the close PK parameters between the Chinese and Japanese populations, AUC24,ss of these two ethnic groups with 15 mg q24h were also similar. Considering that a lower dose of 15 mg was approved in Japan as a standard dose and that its safety and efficacy have been demonstrated in many clinical studies [12, 20, 21, 41, 42], this may further support applying the low rivaroxaban dose from the Japanese population to the Chinese population.

Our study demonstrated the large effect of renal function on exposure and the requirement of a lower dose for patients with moderate impaired renal function. Compared with patients (eGFR 80 mL/min, TBIL 12 μmol/L) taking 15 mg, those with eGFR 30–49 mL/min experienced an ~29%–68% increase in AUC24,ss. This finding was consistent with a previous study in a Caucasian population, which indicated a 1.52-fold (90% confidence interval 1.15–2.01) increase in AUC24,ss for patients with eGFR 30–49 mL/min [43]. The median AUC24,ss of patients with eGFR 30–49 mL/min taking 10 mg were ~2560–3354 μg·h·L−1, which is similar to the exposure of patients with eGFR 80 mL/min taking 15 mg. Therefore, dose reduction is warranted in patients with renal impairment to avoid overexposure.

PT, reflecting the effect of rivaroxaban on coagulation stimulated via the extrinsic pathway of the procoagulant cascade [44, 45], was used as a PD parameter in our study. It was also the most commonly used PD marker in previous population PK-PD studies of rivaroxaban [14, 15, 27, 37, 46,47,48,49,50]. Although there is no well-recognized PD marker for rivaroxaban, PT is regarded as a biomarker to confirm the presence of rivaroxaban [51]. Moreover, PT was reported to be closely correlated with the risk of major bleeding according to the FDA [52], and a prolonged PT also indicates an increased risk of bleeding [53, 54]. Other PD parameters used previously, including activated partial thromboplastin time, prothrombinase-induced clotting time (PiCT) and Heptest [14, 27, 50], lack evidence of clinical relevance till now.

Meanwhile, it should be noted that the international normalized ratio (INR) should not be used to monitor rivaroxaban [51]. When converting PT to INR using the manufacturer-provided generic international sensitivity index (ISI) values, there is more pronounced variability, making it unreliable for clinical monitoring [55, 56]. This is because the ISI was developed from patients treated with warfarin and is not suitable for PT prolonged by factor Xa inhibitors [57].

The estimate of baseline PT in our study (13.9 s) was comparable with previous reports in Japanese patients (11.4–14 s) [14, 15, 37] and non-Japanese patients (11.4–13.9 s) [27, 47,48,49,50]. The estimate of slope in our study (0.0133 s·L·μg−1) was similar to the reported value in a study conducted in Japanese NVAF patients using the same PT bioassay (0.0158 s·L·μg−1) [37]. This indicates that there may be no obvious differences in the PT responses between Chinese and Japanese individuals.

In our study, TBIL and eGFR were detected as significant covariates of PT baseline. The effect of liver and kidney function on PT has also been reported in previous studies [15, 27, 47,48,49]. PT may be prolonged when clotting factors are deficient or inhibited due to other factors such as medication, liver disease, and vitamin K deficiency [44, 45]. Many clotting factors are synthesized by the liver and are reduced when the liver is damaged, which consequently leads to prolonged PT [45]. TBIL level is an important variable in the Child–Pugh score system for assessing the prognosis of chronic liver disease, and it may increase in cholestatic or hepatocellular diseases [23, 58]. The association between eGFR and PT may be explained by the prevalent suboptimal vitamin K status in patients with chronic kidney disease [59, 60]. Regardless, the extent to which PT changes are clinically relevant is still unclear. The overall effect of TBIL and eGFR on PT might be minor, and the maximum change in PTave,ss was ~26% in our study.

As with the current package insert, from a PK perspective, we also demonstrated the requirement for dose reductions in patients with moderately impaired renal function. Moreover, we found that patients with normal or mildly impaired liver function had a higher PT level, even after dose adjustment based on renal function. Previous studies had explored the effect of impaired renal function or liver function alone based on the PK and/or PD of rivaroxaban and well documented in the package insert [9, 43, 61], but it should be aware that there are patients with both impaired liver and renal function. Although the clinical relevance of an elevated PT is still unclear, clinicians should still pay more attention to these vulnerable patients, considering the relationship between elevated PT and the risk of major bleeding [52, 62].

Several studies have investigated the effect of genetic polymorphisms of ABCB1 on the PK of rivaroxaban [63,64,65,66]. However, only one study with a large sample size (n = 156) detected the relationship between ABCB1 rs1128503 variant and rivaroxaban trough concentration (P < 0.05) [66]. The inconsistency of the research results indicates that the ABCB1 genotype may not be a significant covariate for the PK of rivaroxaban. In the present study, the ABCB1 rs4148738 genotype was statistically significant for CL/F but without clinical relevance (<20%); accordingly, dose adjustment based on genotype does not appear to be warranted. Moreover, our study further found that genetic polymorphisms of ABCG2 and CYP3A4/5 had little impact on rivaroxaban clearance.

Our study has several limitations. First, limited samples in the absorption phase were obtained; thus, ka could not be estimated; instead, we applied values reported in a previous study [15]. In addition, we could not estimate the BSV of V/F and determine the covariates on V/F either, because the majority of collected samples in our study represented the trough concentration. However, CL/F is a more important index for patients with long-term pharmacotherapy, and the CL/F and the impacts of its covariate could be precisely estimated [67]. Second, PT tests might not be the optimal PD marker for rivaroxaban, which limits the interpretation of PT changes. Third, limited patients with eGFR < 30 mL/min and TBIL > 34 μmol/L were included in our study. Our findings may not be extrapolated to this particular population and may require further investigation.

In conclusion, a population PK-PD model of rivaroxaban was developed based on Chinese patients with NVAF. The eGFR and TBIL levels affected the PK-PD characteristics of rivaroxaban. Model-based simulation suggests that 15 mg of rivaroxaban in Chinese patients with normal renal and liver function provided a similar exposure compared with 20 mg in Caucasian patients. A lower dose is recommended for patients with renal impairment to avoid overexposure. Additionally, patients with eGFR ≤ 30 mL/min accompanied by TBIL ≥ 34 μmol/L had a higher PT level, even when the dose was adjusted according to renal function, which requires more attention with respect to the risk of major bleeding. Population PK-PD analyses could provide individualized dosing strategies considering both kidney and liver function in Chinese NVAF patients taking rivaroxaban for stroke prevention.