Abstract
Weak measurement has provided new insight into the nature of quantum measurement, by demonstrating the ability to extract average state information without fully projecting the system. For single-qubit measurements, this partial projection has been demonstrated with violations of the Leggett–Garg inequality. Here we investigate the effects of weak measurement on a maximally entangled Bell state through application of the Hybrid Bell–Leggett–Garg inequality (BLGI) on a linear chain of four transmon qubits. By correlating the results of weak ancilla measurements with subsequent projective readout, we achieve a violation of the BLGI with 27 s.d.s. of certainty.
Similar content being viewed by others
Introduction
Quantum computing promises greater processing power through the clever application of superposition and entanglement. Despite the importance of this uniquely quantum behaviour, it occurs elusively behind the non-unitary effects of measurement collapse. Weak measurements1–3 have provided new insight into this process by demonstrating the ability to extract average state information without fully collapsing the system. These gentler measurements have allowed single-configuration violations of the Leggett–Garg inequality4–11 and, more trecently, the detailed tracking of single-qubit trajectories.12,13 It is an outstanding challenge, however, to achieve the same level of measurement control with an entangled state. Here we demonstrate a continuous and controlled exchange between extracted single-qubit state information and two-qubit entanglement collapse, through the unique framework of the Bell–Leggett–Garg inequality (BLGI). We quantify this effect by correlating variable strength ancilla qubit measurements with subsequent projective readout to collect all the statistics of a Bell inequality experiment14–17 in a single quantum circuit. In addition, we demonstrate the ability to measure the Bell state with minimal entanglement collapse, by violating this hybrid BLGI18 at the weakest measurement strengths. This experiment indicates that it is possible carry out high-fidelity ancilla measurement in large entangled systems. In addition, combining this experiment with remote entanglement methods19 may eventually lead to a loophole-free violation of classical hidden variable theories.
The challenge of successfully implementing weak measurements is twofold: the first challenge is to evaluate the amount of information extracted on average by the measurement; the second challenge is to evaluate the measurement back-action on the system. For a single-qubit state, the Leggett–Garg inequality20 (LGI) provides an elegant way to do both with a single experiment. The LGI was originally designed to verify the ‘quantumness’ of macroscopic objects through the effects of projective measurement, which allows larger correlations between successive measurements (e.g., at times t1<t2<t3) than are possible classically. More recent generalisations of the LGI prepare a known state at time t1 and replace the intermediate measurement at time t2 with a weak measurement.4–11 This minimises the quantum-state disturbance while still extracting sufficient information on average. Ideally, this allows all the statistics necessary for a violation of the inequality to be measured with a single experimental configuration. Violating the inequality in this way guarantees that the state information has been extracted without significant back-action on the system.7
Evaluating the effect of weak measurements on an entangled state is more difficult because the degree of entanglement is generally challenging to quantify. The most robust method for quantifying entanglement remains a Bell test,14 which was first proposed by Bell and later refined by Clauser, Horne, Shimony and Holt into an inequality (CHSH). The CHSH term sums the correlation measurements of two spatially separated qubits in four different measurement bases and bounds the maximum total value of classical correlations to be .
In superconducting qubits, we use qubit state rotations to map the desired measurement basis onto the ground and excited states of the system. For measurement rotations a (qubit 1) and b (qubit 2), the correlation amplitude between two measurements is given by
where the term P(00) is the probability that both qubits are in the ground state. A traditional CHSH experiment combines the four correlator terms
Entangled quantum states can violate the classical bound, with a fully entangled Bell state ideally saturating the quantum upper bound of at the specific rotation angles a=0, b=π/4, a′=π/2 and b′=3π/4.
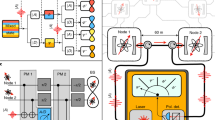
To understand the effect of weak measurement on an entangled state, we combine the spatial correlations of a Bell inequality with the temporal correlations of an LGI to construct a BLGI. The algorithm, as described by Dressel and Korotkov18 and shown in Figure 1, consists of a CHSH-style experiment in which each Bell qubit is measured twice in succession as for a simultaneous LGI.7,10,27 The initial measurements are carried out by ancilla qubits, which act as probes of the entangled system before being projectively read out. By varying the degree of entanglement between each ancilla and the Bell qubit it probes, we can vary the strength of the measurement. After preparing the Bell qubits in the anti-symmetric singlet state
each Bell qubit (β1,2) is rotated to its first measurement angle (a=0, b=π/4) and then entangled with its ancilla qubit (α1,2) to implement the tunable-strength measurement. Next, each Bell qubit is rotated to its final measurement angle (a′=π/2, b′=3π/4), and all four qubits are read out. With this procedure, the data for each measurement angle are encoded on a distinct qubit (a→α1, b→α2, a′→β1, and b′→β2). The BLGI correlator then takes the form similar to equation (2)
where each term is calculated as in equation (1).
Schematic of the hybrid Bell–Leggett–Garg inequality and optical micrograph of the superconducting quantum device. The algorithm consists of two LGI weak measurement branches, bridged by the entanglement of the central Bell qubits. The Bell pair (β1,2) is initially prepared in the anti-symmetric singlet Bell state . Next, each Bell qubit is rotated to its first measurement basis (a or b) and entangled with its ancilla qubit (α1,2). Finally, the Bell qubits are rotated and projectively read out in bases corresponding to angles a′ and b′. By correlating the final projective readout and the weak ancilla measurements, we calculate all four terms of a CHSH correlator simultaneously.
The BLGI bounds correlations between these four distinct measurements based on the classical assumptions of local-macro-realism18 (See Supplementary Information at link for further discussion of the sample, measurement techniques and mathematical assumptions). Classically, the measurement of one qubit in the Bell pair should have no affect on the other, and the strength of the ancilla measurement should have no effect on the result of the following projective readout. By encoding the measurement result for each rotation angle on an independent qubit, we can test both of these assumptions at the same time. Quantum mechanically, if the ancilla measurement is fully projective then we should measure the expected correlation amplitude of only in the initial measurement basis, as the Bell qubits are no longer entangled after that measurement. As the ancilla measurement strength is decreased, we should extract the same qubit information on average while only partially collapsing the Bell state. For sufficiently weak measurements, the magnitudes of all four correlators should approach the unperturbed Bell state values of while approaches . Thus, a violation implies that our system demonstrates non-classical correlations through the entanglement of the Bell pair, while also demonstrating the ability to extract average state information without significant back-action on the entanglement of the system.
Results
To quantify the entanglement collapse, we measure each two-qubit correlator in versus ancilla measurement strength ϕ. The data are plotted in Figure 2 alongside theory curves generated by a quantum model that includes realistic environmental dephasing and readout fidelity.18 Error bars for the data represent ±10 s.d. of the mean to demonstrate the increase in noise with decreasing measurement strength. For projective angles ϕ≈π/2, the ancilla measurement results (E(α1, α2)) reflect the correlation expected from a fully collapsed Bell pair. As the measurement strength is decreased, this ancilla correlation remains nearly constant while additional inter-qubit correlations (E(α1, β2), E(β1, α2), E(β1, β2)) emerge. For sufficiently weak measurements, exceeds the classical bound of 2 and saturates towards the CHSH value of 2.5, which is expected from simulations for a fully entangled Bell state in realistic experimental conditions (see Supplementary Information at link for further discussion of the sample, measurement techniques and mathematical assumptions).
Graph showing both experimental data (points) and theoretical predictions (lines) for the correlator and its four terms versus measurement strength ϕ. The horizontal gold line denotes the classical bound on . The data set was taken by averaging together 200 traces in which each point was measured 3,000 times for a total of 600,000 iterations per point. The error bars represent 10 s.d. of the mean to demonstrate the scaling of the ancilla measurement noise versus ϕ. The magnitude of the correlations between each pair of qubits reveals the extent to which entanglement has been broken for each measurement strength.
The measured BLGI correlations follow the theoretical model very closely for all measurement strengths (see Supplementary Information at link for further discussion of the sample, measurement techniques, and mathematical assumptions). This behaviour reveals the continuous and controlled exchange between the collapse of an entangled Bell state and the single-qubit state information gained from tunable-strength measurements. Each ancilla qubit, when calibrated, retains the same correlations for all measurement strengths, whereas each Bell qubit has its correlations damped through partial projection by its ancilla qubit.18 The effect of partial projection can be seen in the difference in functional behaviour between the Bell-ancilla (E(α1, β2), E(β1, α2)) and the Bell–Bell (E(β1, β2)) correlator terms. In the Bell-ancilla terms, the correlations are suppressed solely because of the randomisation of the Bell qubit, but they return as soon as measurement strength is decreased. In the Bell–Bell term, this effect is compounded, as both qubits are being damped by partial ancilla projection, and thus the correlations return more slowly. This gives E(β1, β2) its distinct shape compared with the other correlators. The BLGI terms can be seen in greater detail in the Supplementary Information (see Supplementary Information at link for further discussion of the sample, measurement techniques and mathematical assumptions).
Discussion
Although other methods exist to characterise entanglement, the correlation measurements of a CHSH experiment remain one of the more robust tests of quantum behaviour because of the considerations given to experimental loopholes. Fortunately, the unique construction of the BLGI allows us to avoid some of the more pervasive loopholes appearing in traditional Bell or LG inequalities. The simultaneous measurement of all four CHSH terms in a single circuit allows us to avoid any configuration-dependent bias, such as the disjoint sampling loophole.21 The near unit detection efficiency in superconducting systems (See Supplementary Information at link for further discussion of the sample, measurement techniques, and mathematical assumptions)22 similarly bypasses the fair sampling loophole,23 which has hindered the investigation of related hybrid inequalities in optical systems.9,24 In addition, as the data from each ancilla qubit are only correlated with the data from the Bell and ancilla qubits on the remote LGI branch, we can substantially relax the usual LGI noninvasive measurement assumption to the standard locality assumption needed for a Bell inequality instead.
This locality assumption, fundamental to any Bell inequality, presumes that no classical interactions between remote qubits occur during the correlation measurements. The close proximity of adjacent superconducting qubits on a chip implies that such an interaction cannot be ruled out here. Thus, behaviour that appears to be quantum could, at least in principle, be the result of a fast classical interaction between hidden variables in the system. Although we cannot yet completely rule out these local interactions, there are several promising approaches to closing this loophole as well. The assumptions of the BLGI requires only spatial separation of the central Bell qubits. The speed and fidelity of operations in a superconducting qubit system makes modest spatial separation sufficient, and we can sacrifice some Bell state preparation fidelity to achieve it. Techniques such as remote entanglement through measurement,19 may soon provide the spatial separation necessary to conduct a loophole-free BLGI experiment.
Despite the few remaining loopholes, the excellent agreement between data and theoretical predictions in this experiment allows us to draw certain likely conclusions about the application of ancilla measurement in superconducting circuit systems. The functional dependence of the BLGI correlator on measurement strength implies that the back-action is dominated by the projectiveness of the measurement. This makes it unlikely that there is some poorly understood classical error mechanism that would make it difficult to implement error correction schemes such as the surface code,25 which rely on sequential high-fidelity ancilla measurements to detect errors.26 The violation of the BLGI at the weakest measurement strength also implies that it is possible to extract average state information without significant back-action. Normally, the usefulness of this type of measurement is limited by the large number of statistics required to average the noisy detector output and the coherence time of the qubits limiting the total number of measurements. It should be possible, however, to integrate weak ancilla measurements into a large surface code cell, which would correct for most errors while also allowing for a larger ensemble to be collected from the weak measurement. Thus, weak ancilla measurement could become an important tool in understanding the dynamics of large quantum systems.
In the course of this work, we have demonstrated the continuous and controlled collapse of an entangled state based on the strength of tunable ancilla measurements. This behaviour was quantified using the simultaneous correlation measurements that make up the Bell–Leggett–Garg inequality. The violation of this inequality at the weakest measurement strengths demonstrates the viability of using weak ancilla measurements to conduct many sequential measurements of entangled states. This provides a window into the evolution of entangled states, which is a critical component in scaling to larger quantum systems. With the inclusion of new remote entanglement algorithms, the BLGI may also lead to loophole-free violations of classical hidden variable theories. Last, this demonstrates that as we scale to larger multi-qubit systems, with the fidelity and control achieved here, we gain greater access to the rich physics at the heart of quantum mechanics.
Materials and methods
We performed this experiment on a linear chain of Xmon transmon qubits, shown at the top of Figure 1, with ground to excited state transition frequencies in the 4–6 GHz range.26 Each qubit is individually addressed with a microwave control line, which can be used for single-qubit X or Y gates, as well as a DC line for implementing Z-gates and frequency control. These control lines are used in conjunction to execute high-fidelity two-qubit gates28 for entanglement and ancilla measurement. The state of each qubit is measured independently using the dispersive shift of a dedicated readout resonator. Resonators are frequency multiplexed29 and read out with a broadband parametric amplifier,30 which allows for fast high-fidelity measurement. Further details of this device can be found in ref. 26 (See Supplementary Information at link for further discussion of the sample, measurement techniques and mathematical assumptions).
The ancilla measurement protocol used in this experiment and shown in Figure 3 is a modified version of the protocol demonstrated in an LGI violation from Groen et al.10 Initially, an ancilla qubit is Y-rotated by an angle 0⩽ϕ ⩽π/2 from its ground state to set the measurement strength. A control phase gate is then performed, causing a Z rotation of π/2 in the ancilla qubit depending on the target qubit’s state. Finally, a −Y rotation of π/2 is performed on the ancilla qubit to rotate into the correct measurement basis. The visibility of this measurement is then proportional to the distance of the ancilla state vector from the equator of the Bloch sphere, as shown in Figure 3b. When ϕ=π/2, this operation becomes a control-NOT gate and implements a projective measurement. As ϕ→0 the ancilla states become degenerate and no information is extracted.
Weak measurement protocol. (a) Full pulse sequence of the ancilla measurement algorithm used in the BLGI experiment. The measurement consists of a variable-amplitude Y rotation by an angle ϕ, which controls the strength of the measurement. This is followed by a CZ gate that entangles the ancilla qubit with the target qubit. Finally, the ancilla is rotated by an angle −π/2, bringing it into the desired measurement basis. Two cases are compared: that of the target qubit in the ground (blue) or excited (red, π rotation) state. (b) Bloch sphere representation of the ancilla qubit during the weak measurement protocol when the target qubit is in either the ground (blue) or excited (red) state. The Z averages of the ancilla and target qubit are correlated such that , where a full projective measurement corresponds to ϕ=π/2 and no measurement corresponds to ϕ=0. (c) Ancilla measurement of prepared target state before and after calibrating for measurement strength. We calibrate both curves by the scaling factor required to normalise the average 0 state curve. This is almost equivalent to dividing by sin (ϕ) but bounds the calibrated mean by ±1. In the calibrated case, the measured mean remains unchanged while the measured variance increases as ϕ decreases. The gold-shaded region denotes angles at which weak measurement data can violate the BLGI while still being reliably calibrated.
As the final position of the ancilla state is dependent on the measurement strength, the ancilla readout is imperfectly correlated with the target qubit. That is, the visibility of an ancilla Z average, , is compressed from the target Z average by a factor of approximately sin (ϕ). To reconstruct the target Z average from the ancilla Z average, we should thus rescale the signal by 1/sin (ϕ). Initially, this was done by a linear fit of the rotation angle ϕ to the qubit drive amplitude. Unfortunately, this linear fit was too rough to properly calibrate the smallest drive amplitudes and led to a systemic offset in the calibration of . To keep the model as simple as possible, we kept the linear fit but used a data-based rescaling to set the measured ground state average to 1, which ensures that the calibrated ancilla average is properly bounded by ±1, as shown in Figure 3c. Further details of this calibration can be found in the Supplementary Information (See Supplementary Information at link for further discussion of the sample, measurement techniques and mathematical assumptions).
References
Kraus, K . States, Effects and Operations (Springer, 1983); URL: http://cds.cern.ch/record/98619.
Aharonov, Y., Albert, D. Z. & Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351 (1988).
Hatridge, M. et al. Quantum back-action of an individual variable-strength measurement. Science 339, 178–181 (2013).
Ruskov, R., Korotkov, A. N. & Mizel, A. Signatures of quantum behavior in single-qubit weak measurements. Phys. Rev. Lett. 96, 200404 (2006).
Jordan, A. N., Korotkov, A. N. & Büttiker, M. Leggett-Garg inequality with a kicked quantum pump. Phys. Rev. Lett. 97, 026805 (2006).
Williams, N. S. & Jordan, A. N. Weak values and the Leggett-Garg inequality in solid state qubits. Phys. Rev. Lett. 100, 026804 (2008).
Palacios-Laloy, A. et al. Experimental violation of a Bell/’s inequality in time with weak measurement. Nat. Phys. 6, 442–447 (2010).
Goggin, M. E. et al. Violation of the leggett-garg inequality with weak measurements of photons. Proc. Natl Acad. Sci. USA 108, 1256–1261 (2011).
Dressel, J., Broadbent, C., Howell, J. & Jordan, A. Experimental violation of two-party Leggett-Garg inequalities with semiweak measurements. Phys. Rev. Lett. 106, 040402 (2011).
Groen, J. et al. Partial-measurement backaction and nonclassical weak values in a superconducting circuit. Phys. Rev. Lett. 111, 090506 (2013).
Emary, C., Lambert, N. & Nori, F. Leggett-garg inequalities. Rep. Prog. Phys. 77, 016001 (2014).
Murch, K., Weber, S., Macklin, C. & Siddiqi, I. Observing single quantum trajectories of a superconducting quantum bit. Nature 502, 211–214 (2013).
Weber, S. et al. Mapping the optimal route between two quantum states. Nature 511, 570–573 (2014).
Bell, J. S. et al. On the einstein-podolsky-rosen paradox. Physics 1, 195–200 (1964).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880 (1969).
Aspect, A., Grangier, P. & Roger, G. Experimental realization of einstein-podolsky-rosen-bohm gedankenexperiment: a new violation of Bell’s inequalities. Phys. Rev. Lett. 49, 91 (1982).
Clauser, J. F. & Shimony, A. Bell’s theorem. experimental tests and implications. Rep. Prog. Phys. 41, 1881 (1978).
Dressel, J. & Korotkov, A. N. Avoiding loopholes with hybrid Bell-Leggett-Garg inequalities. Phys. Rev. A 89, 012125 (2014).
Roch, N. et al. Observation of measurement-induced entanglement and quantum trajectories of remote superconducting qubits. Phys. Rev. Lett. 112, 170501 (2014).
Leggett, A. J. & Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 54, 857 (1985).
Larsson, J.-Å. Bell’s inequality and detector inefficiency. Phys. Rev. A 57, 3304 (1998).
Ansmann, M. et al. Violation of bell’s inequality in Josephson phase qubits. Nature 461, 504–506 (2009).
Pearle, P. M. Hidden-variable example based upon data rejection. Phys. Rev. D 2, 1418 (1970).
Higgins, B., Palsson, M., Xiang, G., Wiseman, H. & Pryde, G. Using weak values to experimentally determine "negative probabilities" in a two-photon state with Bell correlations. Phys. Rev. A 91, 012113 (2015).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: Towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015).
Marcovitch S., Reznik B . Testing Bell inequalities with weak measurements. Preprint at http://arxiv.org/abs/1005.3236 (2010).
Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503 (2014).
Chen, Y. et al. Multiplexed dispersive readout of superconducting phase qubits. Appl. Phys. Lett. 101, 182601–182601 (2012).
Mutus, J. et al. Strong environmental coupling in a Josephson parametric amplifier. Appl. Phys. Lett. 104, 263513 (2014).
Acknowledgements
This work was supported by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), through the Army Research Office grant W911NF-10-1-0334. All statements of fact, opinion or conclusions contained herein are those of the authors and should not be construed as representing the official views or policies of IARPA, the ODNI or the US Government. Devices were made at the UC Santa Barbara Nanofabrication Facility, a part of the NSF-funded National Nanotechnology Infrastructure Network, and at the NanoStructures Cleanroom Facility.
Author information
Authors and Affiliations
Contributions
TCW and JYM performed the experiment and analysed the data. JD designed the experiment together with TCW, and JYM, JK, AEM and RB fabricated the sample. TCW, JYM and JMM co-wrote the manuscript. All authors contributed to the fabrication process, experimental setup and manuscript preparation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies the paper on the npj Quantum Information website (http://www.nature.com/npjqi)
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
White, T., Mutus, J., Dressel, J. et al. Preserving entanglement during weak measurement demonstrated with a violation of the Bell–Leggett–Garg inequality. npj Quantum Inf 2, 15022 (2016). https://doi.org/10.1038/npjqi.2015.22
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjqi.2015.22
This article is cited by
-
Interactive simulation of quantum key distribution protocols and application in Wi-Fi networks
Wireless Networks (2023)
-
Experimental test of non-macrorealistic cat states in the cloud
npj Quantum Information (2020)
-
Benchmarks of nonclassicality for qubit arrays
npj Quantum Information (2019)
-
Entanglement protection in Jaynes–Cummings model
Quantum Information Processing (2019)
-
Overcoming experimental limitations in a nonlinear two-qubit gate through postselection
Quantum Information Processing (2017)