Abstract
Topological Weyl semimetal (TWS), a new state of quantum matter, has sparked enormous research interest recently. Possessing unique Weyl fermions in the bulk and Fermi arcs on the surface, TWSs offer a rare platform for realizing many exotic physical phenomena. TWSs can be classified into type-I that respect Lorentz symmetry and type-II that do not. Here, we directly visualize the electronic structure of MoTe2, a recently proposed type-II TWS. Using angle-resolved photoemission spectroscopy (ARPES), we unravel the unique surface Fermi arcs, in good agreement with our ab initio calculations that have nontrivial topological nature. Our work not only leads to new understandings of the unusual properties discovered in this family of compounds, but also allows for the further exploration of exotic properties and practical applications of type-II TWSs, as well as the interplay between superconductivity (MoTe2 was discovered to be superconducting recently) and their topological order.
Similar content being viewed by others
Introduction
Three-dimensional (3D) topological Weyl semimetals (TWSs) are novel topological quantum materials discovered and intensively investigated recently because of their intimate link between concepts of different fields of physics and material science, as well as the broad application potential1,2,3,4,5,6. In a TWS, low-energy electronic excitations form composite Weyl fermions dispersing linearly along all the three momentum directions across the Weyl points (WPs)7,8,9,10 that always appear in pairs with opposite chirality. Between WPs of different chirality, there exist intriguing surface Fermi arcs, the unconventional open curve-like Fermi surfaces (FSs) with nondegenerate spin texture. The exotic bulk and surface electronic structures thus provide an ideal platform for many novel physical phenomena, such as negative magnetoresistance, anomalous quantum Hall effect and chiral magnetic effects11,12,13,14,15,16,17,18,19,20.
Interestingly, the TWSs can be further classified into two types by Fermiology and whether the Lorentz symmetry is respected: type-I TWS that hosts point-like bulk FSs formed solely by WPs that approximately respect the Lorentz symmetry4,5,6; and type-II TWS that breaks the Lorentz symmetry and harbours finite electron density of states at the Fermi energy . Recently, type-I TWSs have been discovered in the (Ta, Nb) (As, P) family of compounds7,8,9,21,22. However, the complex 3D crystal structure in these first-generation TWSs may pose difficulties in the exploration of their practical applications, and their large number (12 pairs) of WPs could make the exploration of novel physical phenomena complicated. Therefore, new TWS materials easier to process, more friendly to device fabrication applications and with less WPs are desired.
More recently, type-II TWS has been proposed to exist in layered transition metal dichalcogenides (TMDs, for example, WTe2, MoTe2 and WxMo1-xTe2)23,24,25,26. The distribution of the WPs is found to be very sensitive to the lattice parameters. Even a small difference of the lattice constant (∼0.5%) will change the number of WPs in the Brillouin zone (BZ) and lead to different topology of the surface Fermi arcs23,27. With less WPs and nonvanishing electronic density of states at the Fermi surface, type-II TWSs in TMD compounds are expected to show very different properties from the type-I TWSs, such as anisotropic chiral anomaly depending on the current directions, a novel anomalous Hall effect24. In addition, the layered nature of the TMD TWSs greatly facilitates the fabrication of devices28, making them an ideal platform for the realization of novel TWS applications.
In this work, using high-resolution angle-resolved photoemission spectroscopy (ARPES), we systematically study the electronic structure of the orthorhombic (Td)-MoTe2. By carrying out broad-range photon energy-dependent measurements, we can conclude that the observed surface Fermi arcs are consistent with previous23 and our ab initio calculations that are topologically nontrivial. The discovery of the TWS phase in MoTe2 could also help understand the puzzling physical properties in the orthorhombic phase of TMDs recently observed29, and provide a more feasible material platform for the future applications of TWSs because of their layered structures. Furthermore, with the recent discovery of superconductivity in MoTe2 (ref. 25), it even provides an ideal platform for the study of interplays between superconductivity and the nontrivial topological order.
Results
Sample characterization
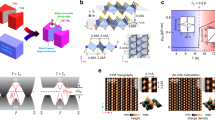
The illustration of the type-I and type-II Weyl fermions is shown in Fig. 1a. Figure 1b,c shows the distributions of the WPs of Td-MoTe2 in the 3D momentum pace and momentum–energy space, respectively. Figure 1d,e present the 3D BZ of Td-MoTe2 and its projected surface BZ with calculated Fermi surface. The crystal structure of Td-MoTe2 is illustrated in Fig. 1f, clearly showing an alternating stacking of Te-Mo-Te triple layer structure (space group Pmn21). We have synthesized high-quality single crystals for this work: the large flat shinning surface (Fig. 1g, left inset) after in situ cleaving is ideal for ARPES measurements; and the crystal symmetry is verified by the Laue (before cleaving) and low-energy electron diffraction (after cleaving) measurements (Fig. 1g, right inset). The lattice constants of the single crystal here are verified by the X-ray diffraction method to be a=6.335 Å, b=3.477 Å, c=13.883 Å that will result in 8 WPs in the kz=0 plane according to ab inito calculation23,25. The core-level photoemission spectrum clearly shows the characteristic Te4d and Mo4p/4s peaks (Fig. 1g), and the broad Fermi surface mapping in Fig. 1h covering multiple BZs confirmed the (001) cleave plane with correct lattice constant. In Fig. 1h, one can already see that the shape of the FS is in general agreements with our calculation (Fig. 1e).
(a) Schematic illustration of type-I and type-II Weyl fermions and Weyl points in the momentum space. (b) Schematic showing the Weyl points of MoTe2 in a BZ and its projection to the kx–kz plane. (c) Schematic showing the Weyl points in the energy–momentum space and their projection to the kx–E plane. (d) Illustration of the BZ of Td-MoTe2 with high symmetry point marked. (e) Fermi surface by our ab initio calculation, showing the bulk electron, hole pockets and the surface states (marked as SS). (f) Crystal structure of the Td -MoTe2, showing alternating ‘…A-B-A-B…’ stacking of MoTe2 layers. (g) Core-level spectrum showing characteristic Mo4s, Te4p/4d core-level peaks. Left inset: cleaved surface of MoTe2 single crystal used in this study. Right insets: Laue and low-energy electron diffraction (LEED) pattern showing the Td phase of MoTe2. (h) Broad-range photoemission spectral intensity map of the Fermi surface (FS) covers >10 BZs, showing the correct symmetry and the characteristic FS.
General electronic structure of Td-MoTe2
To investigate the detailed electronic structures, we focus on one BZ by carrying out high-resolution ARPES measurements, and the results are demonstrated in Fig. 2. In Fig. 2a, the semimetallic nature of Td -MoTe2 can be clearly seen, where large hole pockets are centred around  and electron pockets are away from
and electron pockets are away from  along the
along the  direction. The evolution of these pockets with binding energy is illustrated in the dispersion plots (Fig. 2b–e) and the bands’ constant energy contours (Fig. 2f–o). In Fig. 2b,c, the strongly anisotropic band dispersion along the
direction. The evolution of these pockets with binding energy is illustrated in the dispersion plots (Fig. 2b–e) and the bands’ constant energy contours (Fig. 2f–o). In Fig. 2b,c, the strongly anisotropic band dispersion along the  and
and  directions are clearly shown: the hole- and electron-like Fermi crossings are both observed along
directions are clearly shown: the hole- and electron-like Fermi crossings are both observed along  direction, whereas only hole-like Fermi crossings can be observed along
direction, whereas only hole-like Fermi crossings can be observed along  that show broad agreement with our ab initio calculations (Fig. 2d,e). The electron- and hole-pocket evolution can be better seen in Fig. 2f–j, where the outer electron pockets shrink with EB and disappear beyond 0.075 eV, consistent with the dispersion in Fig. 2b,c and also our ab initio calculations (see Fig. 2k,o, and more comparisons between our experimental result and calculations can be found in Supplementary Note 1 and Supplementary Figs 1–3). The evolution of the constant energy contours through a larger energy scale is illustrated in Fig. 2p, showing a rich evolution of texture from multiple bands.
that show broad agreement with our ab initio calculations (Fig. 2d,e). The electron- and hole-pocket evolution can be better seen in Fig. 2f–j, where the outer electron pockets shrink with EB and disappear beyond 0.075 eV, consistent with the dispersion in Fig. 2b,c and also our ab initio calculations (see Fig. 2k,o, and more comparisons between our experimental result and calculations can be found in Supplementary Note 1 and Supplementary Figs 1–3). The evolution of the constant energy contours through a larger energy scale is illustrated in Fig. 2p, showing a rich evolution of texture from multiple bands.
(a) The 3D intensity plot of the photoemission spectra around  , with the electron and hole pockets indicated. (b,c) High symmetry cut along the
, with the electron and hole pockets indicated. (b,c) High symmetry cut along the  and
and  directions, respectively. BCB, bulk conduction band; BVB, bulk valance band. (d,e) The corresponding calculations along the
directions, respectively. BCB, bulk conduction band; BVB, bulk valance band. (d,e) The corresponding calculations along the  and
and  directions, respectively. (f–j) Photoemission spectral intensity map showing the constant energy contours of bands at EB=0, 0.025, 0.05, 0.075 and 0.1 eV, respectively. (k–o) Corresponding calculated constant energy contours at the same binding energies as in experiments above. (p) Stacking plots of constant-energy contours in broader binding energy range show the band structure evolution.
directions, respectively. (f–j) Photoemission spectral intensity map showing the constant energy contours of bands at EB=0, 0.025, 0.05, 0.075 and 0.1 eV, respectively. (k–o) Corresponding calculated constant energy contours at the same binding energies as in experiments above. (p) Stacking plots of constant-energy contours in broader binding energy range show the band structure evolution.
Surface and bulk electronic structures of Td-MoTe2
In order to distinguish the surface and bulk contributions from numerous band dispersions in Fig. 2, we conducted photon energy-dependent ARPES experiment30 with a broad photon energy range of 20–120 eV, covering more than 5 BZs along the kz direction (see Fig. 3a, and more details can be found in Supplementary Note 2 and Supplementary Fig. 4). In Fig. 3a, throughout the whole range, bands with negligible kz dispersion can be observed, showing a clear sign of surface states. By plotting the FSs measured with different photon energies (Fig. 3b–i), one can clearly see that the nondispersive bands along kz in Fig. 3a correspond to the FS features in the narrow region between the bulk and electron pockets (as highlighted by the red rectangles in Fig. 3b–i) that show identical shape under different photon energies, whereas the pockets from the bulk states vary strongly (as also can be seen by the dispersive bands in Fig. 3a). This observation is again in good agreement with the ab initio calculation, as shown in Fig. 3j, where the sharp surface state bands clearly emerge between the electron and hole pockets.
(a) The photoemission spectral intensity map in ky–kz plane, where the red arrows indicate the surface states (marked as SS) that show no dispersion along the kz direction. Red curves indicate the kz locations of different photon energies. (b–i) Fermi surfaces measured under different photon energies as indicated in a. Red dashed rectangles and arrows highlight the position of the surface states that do not change shape with the photon energies. (j) Calculated Fermi surface with black dashed rectangles highlighting the same area as in b–i indicating clear surface states inside.
Surface Fermi arcs in Td-MoTe2
After establishing the overall band structures and the identification of surface state regions, we further zoom in to these regions to search for the characteristic surface Fermi arcs, a hallmark of the electronic structure of a TWS. According to the ab initio calculations, although the WPs lie slightly above the Fermi level (∼26 and 79 meV above the experimental Fermi-level according to the calculations, see ref. 23 and Supplementary Fig. 2 for details), the surface Fermi arcs are still visible, lying within the narrow region between the electron and hole pockets (see Fig. 4a, marked as SA between the points P1 and P2). As there is another surface state (marked as SS) nearby, to best visualize and separate the two surface states, we chose a low (27 eV) photon energy to increase the momentum resolution; also under this photon energy, the bulk states intensity is greatly suppressed and thus the surface states can be easily seen. Indeed, from these fine measurements, the two surface states in the calculations (Fig. 4a–d) are both observed (see Fig. 4e–h, and the measurements from more photon energies can be found in the Supplementary Fig. 5). Interestingly, as the positions of P1 and P2 vary with binding energy (see Fig. 4a–d ), the surface Fermi arcs observed in our measurements (Fig. 4e–h ) also vary accordingly (in shape and length), in good agreement with the calculation, thus strongly supporting their topological origin. To further investigate their spin texture, we have also carried out preliminary spin-resolved ARPES measurements that can be found in the Supplementary Note 3 and Supplementary Fig. 6.
(a–d) Evolution of the projection of the Fermi arcs in the calculation at EB=0, 0.01, 0.02 and 0.04 eV, respectively. The regular surface state and the surface Fermi arc are labelled as SS and SA, respectively; points P1 and P2 indicate the starting and ending points of the surface Fermi arcs. (e–h) Photoemission intensity map in the same area as in a–d. The dashed lines show the surface state (SS) and the surface Fermi arcs (SA), corresponding to those in a–d.
Discussion
Our systematic study on the electronic band structures and the observation of surface Fermi arc states, together with the broad agreement with the ab initio calculations, establish that Td-MoTe2 is a type-II TWS that can not only help understand the puzzling physical properties in the orthorhombic phase of TMDs, but also provide a new platform for the realization of exotic physical phenomena and possible future applications. We note that while we were finalizing this manuscript, three other groups31,32,33 also independently studied this family of compounds and the surface states and arcs.
Methods
Sample synthesis
The chemical vapour transport method was employed to grow MoTe2 crystals using polycrystalline MoTe2 powder and TeCl4 as a transport additive. Here, 1 g of polycrystalline powder and TeCl4 (3 mg ml−1) were sealed in a quartz ampoule that was then flushed with Ar, evacuated, sealed and heated in a two-zone furnace. Crystallization was conducted from (T2) 1,000 to (T1) 900 °C. The quartz ampoule was then quenched in ice water to yield the high-temperature monoclinic phase, the 1T’-MoTe2. When cooling down below ∼250 K, a structural-phase transition occurs from the centrosymmetric 1T’ phase to the noncentrosymmetric Td phase that is the TWS phase, which was known in the resistivity measurement25,34.
Angle-resolved photoemission spectroscopy
Regular ARPES measurements were performed at the beamline I05 of the Diamond Light Source and BL 10.0.1 of the Advanced Light Source, both equipped with Scienta R4000 analyzers. The spin-resolved ARPES experiments were conducted at the beamline APE of the Elettra synchrotron, equipped with a Scienta DA30 analyzer combined with a VLEED spin detector. The measurement sample temperature and pressure were 10 K and <1.5 × 10−10 Torr, respectively. The angle resolution was 0.2° and the overall energy resolutions were better than 15 meV. The samples were cleaved in situ along the (001) plane.
Ab initio calculations
The density functional theory calculations have been performed using the Vienna ab initio simulation package with the projected augmented wave method35 . The exchange and correlation energy was considered in the generalized gradient approximation with Perdew–Burke–Ernzerhof (PBE)-based density functional36. The energy cutoff was set to 300 eV. The tight binding matrix elements were calculated by projecting the Bloch wave functions to maximally localized Wannier functions37. The surface states were calculated from the half-infinite model by using the interative Green’s function method38. The k-dependent local density of states are projected from the half-infinite bulk to the outermost surface unit cell. Experimental lattice constants were used in all the calculations25.
Data availability
The data that support these findings are available from thecorresponding author on request.
Additional information
How to cite this article: Jiang, J. et al. Signature of Type-II Weyl semimetal phase in MoTe2. Nat. Commun. 8, 13973 doi: 10.1038/ncomms13973 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Singh, B. et al. Topological electronic structure and Weyl semimetal in the TlBiSe2 class of semiconductors. Phys. Rev. B 86, 115208 (2012).
Liu, J. & Vanderbilt, D. Weyl semimetals from noncentrosymmetric topological insulators. Phy. Rev. B 90, 155316 (2014).
Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Bulmash, D., Liu, C.-X. & Qi, X.-L. Prediction of a Weyl semimetal in Hg1−x−yCdxMnyTe. Phys. Rev. B 89, 081106 (2014).
Liu, Z. K. et al. Evolution of the Fermi surface of Weyl semimetals in the transition metal pnictide family. Nat. Mater. 15, 27–31 (2016).
Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Xu, S.-Y. et al. Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide. Nat. Phys. 11, 748–754 (2015).
Yang, L. X. et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 11, 728–732 (2015).
Ashby, P. E. C. & Carbotte, J. P. Magneto-optical conductivity of Weyl semimetals. Phys. Rev. B 87, 245131 (2013).
Hosur, P. Friedel oscillations due to Fermi arcs in Weyl semimetals. Phys. Rev. B 86, 195102 (2012).
Huang, X. et al. Observation of the Chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs. Phys. Rev. X 5, 031023 (2015).
Landsteiner, K. Anomalous transport of Weyl fermions in Weyl semimetals. Phy. Rev. B 89, 075124 (2014).
Liu, C.-X., Ye, P. & Qi, X.-L. Chiral gauge field and axial anomaly in a Weyl semimetal. Phys. Rev. B 87, 235306 (2013).
Potter, A. C., Kimchi, I. & Vishwanath, A. Quantum oscillations from surface Fermi arcs in Weyl and Dirac semimetals. Nat. Commun. 5, 5161 (2014).
Shekhar, C. et al. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nat. Phys. 11, 645–649 (2015).
Son, D. T. & Spivak, B. Z. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B 88, 104412 (2013).
Wei, H., Chao, S. P. & Aji, V. Excitonic phases from Weyl semimetals. Phys. Rev. Lett. 109, 196403 (2012).
Xu, G., Weng, H., Wang, Z., Dai, X. & Fang, Z. Chern semimetal and the quantized anomalous Hall effect in HgCr2Se4 . Phys. Rev. Lett. 107, 186806 (2011).
Huang, S. M. et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495–498 (2015).
Sun, Y., Wu, S.-C., Ali, M. N., Felser, C. & Yan, B. Prediction of Weyl semimetal in orthorhombic MoTe2 . Phys. Rev. B 92, 161107 (2015).
Qi, Y. et al. Superconductivity in Weyl semimetal candidate MoTe2 . Nat. Commun. 7, 11038 (2016).
Chang, T.-R. et al. Arc-tunable Weyl Fermion metallic state in MoxW1-xTe2 . Nat. Commun. 7, 10639 (2016).
Wang, Z. J. et al. MoTe2: Weyl and line node topological metal. Phys. Rev. Lett. 117, 056805 (2016).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2 . Nature 514, 205–208 (2014).
Chen, Y. Studies on the electronic structures of three-dimensional topological insulators by angle resolved photoemission spectroscopy. Front. Phys. 7, 175–192 (2011).
Huang, L. et al. Spectroscopic evidence fot type II Weyl semimetal state in MoTe2 . Nat. Mater. 15, 1155–1160 (2016).
Deng, K. et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2 . Nat. Phys. 12, 1105–1110 (2016).
Belopolski, I. et al. Unoccupied electronic structure and signatures of topological Fermi arcs in the Weyl semimetal candidate MoxW1-xTe2. Phys. Rev. B. 94, 085127 (2016).
Hughes, H. P. & Friend, R. H. Electrical resistivity anomaly in b-MoTe2 . J. Phys. C Solid State Phys. 11, L103–L105 (1978).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115 (1993).
Perdew, J. P., Burke, K. & Ernzerho, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Mostofi, A. A. et al. wannier90: a tool for obtaining maximally-localised Wannier functions. Comp. Phys. Commun. 178, 685 (2008).
Lopez Sancho, M. P., Lopez Sancho, J. M. & Rubio, J. Quick iterative scheme for the calculation of transfer matrices: application to Mo (100). J. Phys. F Met. Phys. 14, 1205–1215 (1984).
Acknowledgements
This work is supported by grant from CAS-Shanghai Science Research Center, Grant No: CAS-SSRC-YH-2015-01. This work has been partly performed in the framework of the nanoscience foundry and fine analysis (NFFA-MIUR Italy) project. Y.L.C. acknowledges the support of the EPSRC Platform Grant (Grant No EP/M020517/1) and Hefei Science Center CAS (2015HSC-UE013). C.F. acknowledges the financial support by the ERC Advanced Grant (No 291472 ‘Idea Heusler’). Advanced Light Source is operated by Office of Basic Energy Science of US DOE (contract DE-AC02-05CH11231). C.-C.H. and J.J. acknowledge the support of the NRF, Korea through the SRC Center for Topological Matter (No 2011-0030787).
Author information
Authors and Affiliations
Contributions
Y.L.C. conceived the experiments. J.J. and Z.K.L. carried out ARPES measurements with the assistance of H.F.Y. and C.C. Z.K.L. and H.F.Y. carried out Spin ARPES measurement with the help of I.V. and J.F. C.R.R. and Y.P.Q. synthesized and characterized the bulk single crystals. B.H.Y. and Y.S. performed ab initio calculations. All authors contributed to the scientific planning and discussions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-6 and Supplementary Notes 1-3 (PDF 864 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Jiang, J., Liu, Z., Sun, Y. et al. Signature of type-II Weyl semimetal phase in MoTe2. Nat Commun 8, 13973 (2017). https://doi.org/10.1038/ncomms13973
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13973
This article is cited by
-
Intercalation in 2D materials and in situ studies
Nature Reviews Chemistry (2024)
-
Phase-selective in-plane heteroepitaxial growth of H-phase CrSe2
Nature Communications (2024)
-
Realization of practical eightfold fermions and fourfold van Hove singularity in TaCo2Te2
npj Quantum Materials (2023)
-
Coupled ferroelectricity and superconductivity in bilayer Td-MoTe2
Nature (2023)
-
Measurement of the electronic structure of a type-II topological Dirac semimetal candidate VAl3 using angle-resolved photoelectron spectroscopy
Tungsten (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.