Abstract
Spin chains are paradigmatic systems for the studies of quantum phases and phase transitions, and for quantum information applications, including quantum computation and short-distance quantum communication. Here we propose and analyse a scheme for conditional state transfer in a Heisenberg XXZ spin chain which realizes a quantum spin transistor. In our scheme, the absence or presence of a control spin excitation in the central gate part of the spin chain results in either perfect transfer of an arbitrary state of a target spin between the weakly coupled input and output ports, or its complete blockade at the input port. We also discuss a possible proof-of-concept realization of the corresponding spin chain with a one-dimensional ensemble of cold atoms with strong contact interactions. Our scheme is generally applicable to various implementations of tunable spin chains, and it paves the way for the realization of integrated quantum logic elements.
Similar content being viewed by others
Introduction
Starting with the original proposal by Datta and Das1 for a spin-based field-effect transistor, the field of spintronics2 has explored how the spin degrees of freedom can be used for information transfer. More than two decades later, this research has reached the quantum regime3. One motivation for this is the desire for miniaturization which led to the realization of single-electron transistors4, or more generally single-dopant devices5. A second motivation is the potential applications in quantum information and computation. Two guiding proposals in the field involve implementation of quantum gate operations in quantum dots6 and in doped silicon7. Shortly thereafter, molecular magnets have also been proposed8. It was subsequently shown that universal quantum computation can be realized with Heisenberg exchange interaction, known from quantum magnetism, alone9,10.
Here we put forward a scheme for a quantum spin transistor that may serve as an integral component of quantum information devices. Similarly to the quantum computation proposals, it can be implemented with architectures that realize a Heisenberg spin chain. Various physical realizations of spin chains are being actively explored for short-range quantum state transfer required to integrate and scale-up quantum registers involving many qubits11,12,13,14,15. In fact, spin chains of the Heisenberg type have been realized in organic and molecular magnets16, quantum dots17, various compounds16,18,19, Josephson junction arrays20, trapped ions21,22, in atomic chains on surfaces23,24,25,26,27 and in thin films or narrow magnetic strips that carry spin waves28,29. Combined with conditional dynamics implementing quantum logic gates, spin chains can greatly facilitate large-scale quantum information processing. While many different implementations of the coherent spin transistor may be possible, here we focus on one such proof-of-concept realization with a small ensemble of strongly interacting cold atoms trapped in a tight one-dimensional potential of appropriate shape. Cold atoms have already been used to realize spin chains, and observations of Heisenberg exchange dynamics30, spin impurity dynamics31 and magnon bound states32 have been reported.
Results
Coherent spin transistor
Our quantum spin transistor works with an arbitrary spin state  at the input port (target spin) which is coherently transferred to the output port, if there are no excited spins in the gate,
at the input port (target spin) which is coherently transferred to the output port, if there are no excited spins in the gate,  . However, if the gate contains an excited stationary spin (control spin),
. However, if the gate contains an excited stationary spin (control spin),  , it completely blocks the transfer of the target spin state between the input and output ports. In other words, we have coherent dynamics for the initial state of the system
, it completely blocks the transfer of the target spin state between the input and output ports. In other words, we have coherent dynamics for the initial state of the system  when the gate contains no spin excitation, but complete absence of dynamics for the state
when the gate contains no spin excitation, but complete absence of dynamics for the state  when the gate contains a single spin excitation. Our scheme thus realizes a quantum logic operation and it can be used to obtain spatially entangled states of target and control spins, as well as to create Schrödinger cat states for a large number of target spins.
when the gate contains a single spin excitation. Our scheme thus realizes a quantum logic operation and it can be used to obtain spatially entangled states of target and control spins, as well as to create Schrödinger cat states for a large number of target spins.
The functionality of the proposed transistor relies on the ability to tune the energy levels of the gate such that one of its states is resonant with the input and output states, resulting in coherent excitation transfer, while the other state of the gate is non-resonant and is used to block the transfer. A system that offers sufficient flexibility to realize this level of control is the Heisenberg XXZ spin- chain in a longitudinal magnetic field. We thus consider a chain of N spin-
chain in a longitudinal magnetic field. We thus consider a chain of N spin- particles described by the XXZ model Hamiltonian (ħ=1)
particles described by the XXZ model Hamiltonian (ħ=1)

where  are the Pauli matrices acting on the jth spin, hj determine the energy shifts of the spin-up and spin-down states playing the role of the local magnetic field, Jj are the nearest-neighbour spin–spin interactions, and Δ is the asymmetry parameter: Δ=0 corresponds to the purely spin-exchange XX model, Δ=1 to the homogeneous spin–spin interaction XXX model, while the limit of |Δ|>>1 leads to the Ising model. We assume a spatially symmetric spin chain with Jj=JN−j and hj=hN+1−j with h1,N=0. Note that we do not specify the sign of Jj, which, therefore, can be positive or negative.
are the Pauli matrices acting on the jth spin, hj determine the energy shifts of the spin-up and spin-down states playing the role of the local magnetic field, Jj are the nearest-neighbour spin–spin interactions, and Δ is the asymmetry parameter: Δ=0 corresponds to the purely spin-exchange XX model, Δ=1 to the homogeneous spin–spin interaction XXX model, while the limit of |Δ|>>1 leads to the Ising model. We assume a spatially symmetric spin chain with Jj=JN−j and hj=hN+1−j with h1,N=0. Note that we do not specify the sign of Jj, which, therefore, can be positive or negative.
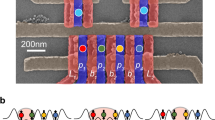
The input and output ports for the target spin are represented by the first j=1 and last j=N sites of the chain, see Fig. 1a. The inner sites j=2,…, N−1 constitute the gate which may be open (Fig. 1b) or closed (Fig. 1c) for the target spin transfer depending on the absence,  , or presence,
, or presence,  , of a single control spin excitation. One might think that the shortest possible spin chain to accommodate a gate between the input and output ports would consist of just N=3 spins. As we show in Supplementary Note 1, however, the three-spin chain cannot implement a reusable spin transistor even in the Ising limit
, of a single control spin excitation. One might think that the shortest possible spin chain to accommodate a gate between the input and output ports would consist of just N=3 spins. As we show in Supplementary Note 1, however, the three-spin chain cannot implement a reusable spin transistor even in the Ising limit  >>1 since the control spin excitation at the gate site j=2 is not protected from leakage. We will therefore illustrate the scheme using a chain of N=4 spins, with the gate consisting of spins j=2,3 coupled to each other via the strong exchange constant
>>1 since the control spin excitation at the gate site j=2 is not protected from leakage. We will therefore illustrate the scheme using a chain of N=4 spins, with the gate consisting of spins j=2,3 coupled to each other via the strong exchange constant  .
.
(a) The ‘in’ and ‘out’ ports are coupled with  to the central ‘gate’ region. (b) The energy levels of the gate, split by ∼Ji/(N−2), are additionally tuned by hj, so as to realize resonant transfer of a spin excitation between the input and output ports when the gate is empty,
to the central ‘gate’ region. (b) The energy levels of the gate, split by ∼Ji/(N−2), are additionally tuned by hj, so as to realize resonant transfer of a spin excitation between the input and output ports when the gate is empty,  . (c) The spin excitation transfer is blocked when the gate contains an excited (control) spin,
. (c) The spin excitation transfer is blocked when the gate contains an excited (control) spin,  . (d) Dynamics of an N=4 spin system with the open or closed gate. The parameters are Δ=−1, h=h−=0 and J2/J1=17.484, as obtained for a system of four atoms in the triple-well potential from equation (2) (V0=500ɛ and U=200ɛ).
. (d) Dynamics of an N=4 spin system with the open or closed gate. The parameters are Δ=−1, h=h−=0 and J2/J1=17.484, as obtained for a system of four atoms in the triple-well potential from equation (2) (V0=500ɛ and U=200ɛ).
Consider a system in the initial state  , which we aim to efficiently transfer to the final state
, which we aim to efficiently transfer to the final state  using an intermediate resonant state, see Fig. 1b and Supplementary Note 2. The initial and final states have the same energy of
using an intermediate resonant state, see Fig. 1b and Supplementary Note 2. The initial and final states have the same energy of  , where h ≡ h2,3 (as is the standard convention in quantum optics, we refer to the expectation value of the Hamiltonian in a given state as the energy of this state). In turn, the eigenstates of Hamiltonian (1) in the single excitation space of strongly coupled sites j=2,3 are given by
, where h ≡ h2,3 (as is the standard convention in quantum optics, we refer to the expectation value of the Hamiltonian in a given state as the energy of this state). In turn, the eigenstates of Hamiltonian (1) in the single excitation space of strongly coupled sites j=2,3 are given by  , with the corresponding energies
, with the corresponding energies  split by 2J2. Then, by a proper choice of the magnetic field,
split by 2J2. Then, by a proper choice of the magnetic field,  , we can tune the energy of one of the intermediate states
, we can tune the energy of one of the intermediate states  into resonance with the initial
into resonance with the initial  and final
and final  states (for example, for h=h− the resonant state is
states (for example, for h=h− the resonant state is  ). Simultaneously, the other intermediate state does not participate in the transfer since its energy is detuned by 2J2 which is much larger than the exchange coupling
). Simultaneously, the other intermediate state does not participate in the transfer since its energy is detuned by 2J2 which is much larger than the exchange coupling  of the initial and final states to the intermediate states. The transfer time of the spin excitation between the initial and final states via a single resonant intermediate state is tout=π/|J1| (Fig. 1d).
of the initial and final states to the intermediate states. The transfer time of the spin excitation between the initial and final states via a single resonant intermediate state is tout=π/|J1| (Fig. 1d).
Next, we place a single spin excitation in one of the eigenstates  of the gate. To be specific, for the magnetic field h=h− we place the control spin in state
of the gate. To be specific, for the magnetic field h=h− we place the control spin in state  and denote it as
and denote it as  . Then the control spin cannot leak out of the gate region and therefore it is stationary. Moreover, if we place a target spin-up at the input port, the resulting state
. Then the control spin cannot leak out of the gate region and therefore it is stationary. Moreover, if we place a target spin-up at the input port, the resulting state  will have the energy
will have the energy  which differs significantly from the energies
which differs significantly from the energies  and
and  of the states to which it can couple via a single spin-exchange (assuming Δ≠0, see below and Supplementary Note 2), see Fig. 1c. Therefore, such an initial state will remain stationary and the control spin excitation on the gate will block the transfer of the target spin between the input and output ports, see Fig. 1d. Indeed, the large energy difference
of the states to which it can couple via a single spin-exchange (assuming Δ≠0, see below and Supplementary Note 2), see Fig. 1c. Therefore, such an initial state will remain stationary and the control spin excitation on the gate will block the transfer of the target spin between the input and output ports, see Fig. 1d. Indeed, the large energy difference  will preclude the escape of the gate spin excitation to the output port, while the large energy mismatch
will preclude the escape of the gate spin excitation to the output port, while the large energy mismatch  will suppress the probability of the second-order exchange of spin excitation between the input and output ports by a factor of
will suppress the probability of the second-order exchange of spin excitation between the input and output ports by a factor of  <<1 (with Δ=−1, see below and Supplementary Note 2). Exactly the same arguments apply to the initial state
<<1 (with Δ=−1, see below and Supplementary Note 2). Exactly the same arguments apply to the initial state  with the magnetic field set to h=h+.
with the magnetic field set to h=h+.
In the same spirit, we can construct spin transistors with longer spin chains (see Supplementary Note 3 for N=5), the above case of N=4 being the shortest and simplest one. The general idea illustrated in Fig. 1a–c is as follows: The gate region consists of N−2 strongly coupled spins,  for all j∈{2,…, N−2}. Therefore, the single excitation space of the gate has N−2 eigenstates
for all j∈{2,…, N−2}. Therefore, the single excitation space of the gate has N−2 eigenstates  split by
split by  . With the magnetic field hj, we tune one of these eigenstates, say
. With the magnetic field hj, we tune one of these eigenstates, say  , in resonance with the single excitation input
, in resonance with the single excitation input  and output
and output  states. Assuming
states. Assuming  , all the other eigenstates
, all the other eigenstates  will remain decoupled during the transfer, and we will have a simple three-level dynamics for a single target spin. Note that if the resonant eigenstate
will remain decoupled during the transfer, and we will have a simple three-level dynamics for a single target spin. Note that if the resonant eigenstate  is antisymmetric, the output state
is antisymmetric, the output state  will be the same as the input state, independent on the sign of Jj (see also Supplementary Note 2), while if we chose symmetric resonant state
will be the same as the input state, independent on the sign of Jj (see also Supplementary Note 2), while if we chose symmetric resonant state  , we would obtain the output state
, we would obtain the output state  which would be identical to the input state upon the application of the Pauli-Z quantum gate (
which would be identical to the input state upon the application of the Pauli-Z quantum gate ( operation) to the output port. To close the transistor gate, we place a single spin excitation in one of the gate eigenstates
operation) to the output port. To close the transistor gate, we place a single spin excitation in one of the gate eigenstates  from where the control spin cannot leak out since this eigenstate is non-resonant. Simultaneously, the target spin cannot enter the gate region since the double-excitation subspace, to which it is coupled, is shifted in energy due to the spin–spin interaction, resulting in the transfer blockade.
from where the control spin cannot leak out since this eigenstate is non-resonant. Simultaneously, the target spin cannot enter the gate region since the double-excitation subspace, to which it is coupled, is shifted in energy due to the spin–spin interaction, resulting in the transfer blockade.
Physical realization
A possible system to realize the spin chain Hamiltonian of equation (1) is a cold ensemble of N strongly interacting atoms in a one-dimensional trap of appropriate geometry33,34,35,36. Recent experiments have confirmed that spin chains may indeed be realized this way37 with tunable microscopic optical traps38. An outline of the procedure to map this system onto the Heisenberg XXZ spin model is presented in Supplementary Note 4. A pair of suitable internal atomic states can serve as the spin-up and spin-down states, with the microwave or radiofrequency transition frequency further tunable through a global magnetic field inducing spatially-uniform Zeeman shifts and by tightly focused non-resonant laser beams inducing site-selective ac Stark shifts 31,39. In the full model, the strong contact interactions between the atoms are described by the dimensionless coefficients  >>1 and g↑↑=g↓↓=κg, where the parameter κ>0 is related to the asymmetry parameter of the effective Heisenberg spin-
>>1 and g↑↑=g↓↓=κg, where the parameter κ>0 is related to the asymmetry parameter of the effective Heisenberg spin- model as
model as  . In turn, the exchange constants of the Heisenberg model
. In turn, the exchange constants of the Heisenberg model  are proportional to the geometric factors αj which are determined by the single particle solutions of the Schrödinger equation in a one-dimensional confining potential V(x). Hence, the shape of the trapping potential can be used to tune the necessary parameters of the effective spin chain34.
are proportional to the geometric factors αj which are determined by the single particle solutions of the Schrödinger equation in a one-dimensional confining potential V(x). Hence, the shape of the trapping potential can be used to tune the necessary parameters of the effective spin chain34.
To realize the Hamiltonian (1) for N=4 particles with  <<1, we use a triple-well potential. This can be modelled in numerous ways, and we choose the physically simple form
<<1, we use a triple-well potential. This can be modelled in numerous ways, and we choose the physically simple form

shown in Fig. 2a (see the caption for the parameters a, b and x0). The potential consists of a shallow Gaussian well at the center and a pair of deeper and narrower wells next to the boundaries. The four lowest-energy single particle wavefunctions of potential (2) are also shown in Fig. 2a. The two lower energy states are nearly degenerate and the corresponding wavefunctions have sizable amplitudes at the deep wells near the boundaries, while the two higher energy states have much larger energy separation, with the amplitudes of the corresponding wavefunctions being large in the shallow well in the middle. Accordingly, the effective exchange interactions satisfy J1=J3 and  <<1. The dependence of the ratio J2/J1 on the parameters V0 and U in equation (2) are shown in Fig. 2b,c.
<<1. The dependence of the ratio J2/J1 on the parameters V0 and U in equation (2) are shown in Fig. 2b,c.
(a) Shape of the potential in equation (2) (thick solid black curve), and single particle eigenfunctions (thinner solid curves) corresponding to the four lowest-energy levels (dashed horizontal lines), for V0=500ɛ and U=200ɛ, where  with m the atom mass. (b) The ratio of exchange coefficients J2/J1 as a function of V0, for U=200ɛ. (c) The ratio of exchange coefficients J2/J1 as a function of U, for V0=500ɛ. Other parameters in equation (2) are
with m the atom mass. (b) The ratio of exchange coefficients J2/J1 as a function of V0, for U=200ɛ. (c) The ratio of exchange coefficients J2/J1 as a function of U, for V0=500ɛ. Other parameters in equation (2) are  ,
,  ,
,  .
.
The nearly perfect transfer, or complete blockade, of the target spin for the open, or closed, gate as shown in Fig. 1d was obtained for the system parameters as in Fig. 2a. It is however important to quantify the sensitivity of the spin transistor to uncontrolled fluctuations of the parameters. In Fig. 3a we show the fidelities  of transfer at time tout=π/|J1| versus the amplitude of random noise affecting the trapping potential or the (effective) magnetic field. We observe that coherent transfer is quite robust with respect to moderate variations in V0, but is rather sensitive to small variations in U and h since they detrimentally affect the gate resonant conditions. Importantly, the gate blockade is virtually unaffected by uncertainties in U, V0, h since it relies on the (large) energy mismatch. In Fig. 3b, we show the dependence of the blockade fidelity
of transfer at time tout=π/|J1| versus the amplitude of random noise affecting the trapping potential or the (effective) magnetic field. We observe that coherent transfer is quite robust with respect to moderate variations in V0, but is rather sensitive to small variations in U and h since they detrimentally affect the gate resonant conditions. Importantly, the gate blockade is virtually unaffected by uncertainties in U, V0, h since it relies on the (large) energy mismatch. In Fig. 3b, we show the dependence of the blockade fidelity  on κ which determines the asymmetry parameter Δ of the XXZ model. Clearly, the spin transistor cannot operate when Δ=0, that is, in the absence of the spin–spin
on κ which determines the asymmetry parameter Δ of the XXZ model. Clearly, the spin transistor cannot operate when Δ=0, that is, in the absence of the spin–spin  interactions, since then the control spin can leak out of the gate, as mentioned above and in Supplementary Note 2.
interactions, since then the control spin can leak out of the gate, as mentioned above and in Supplementary Note 2.
(a) Transfer fidelity F(tout) averaged over 100 independent realizations of the spin chain. In each realization, one of the parameters in A={V0,U,h} is a random variable with the Gaussian probability distribution around the ideal mean A0 (V0=500 ɛ, U=200 ɛ, h=h− or h+), while the other two parameters are kept constant. The s.d. is σA=A0δA and we take σh=h+δh for both h=h± with nearly identical results. (b) The blockade fidelity  for different values of κ (top horizontal axis) or Δ (bottom horizontal axis).
for different values of κ (top horizontal axis) or Δ (bottom horizontal axis).
Discussion
To summarize, we have presented a scheme for a quantum spin transistor realized in a Heisenberg spin chain and proposed and analysed its physical implementation with cold trapped atoms. In our scheme, the presence  or absence
or absence  of a control spin excitation in the gate can block or allow the transfer of an arbitrary target spin state between the input and output ports. If the gate is prepared in a superposition of open and closed states, then the initial state of the system with the target spin-up at the input port will evolve at time tout into the spatially entangled state.
of a control spin excitation in the gate can block or allow the transfer of an arbitrary target spin state between the input and output ports. If the gate is prepared in a superposition of open and closed states, then the initial state of the system with the target spin-up at the input port will evolve at time tout into the spatially entangled state.

Furthermore, if the gate is integrated into a larger system in which the excited spins from the source can be fed (one-by-one or one after the other) into the input port, and the output port is connected to the initially unexcited drain, then the initial gate superposition state will result in a (macroscopically) entangled Schrödinger cat-like state of many spins,

We note that with the atomic realization of spin chains, with the spin-up and spin-down states corresponding to the hyperfine (Zeeman) sublevels of the ground electronic state, the preparation of the closed gate state or the coherent superposition of states  and
and  (assuming h=h−=0) can be accomplished by applying to
(assuming h=h−=0) can be accomplished by applying to  a microwave or two-photon (Raman) optical pulse of proper area (π or π/2) and the frequency matching the energy difference δλ=2J2Δ between
a microwave or two-photon (Raman) optical pulse of proper area (π or π/2) and the frequency matching the energy difference δλ=2J2Δ between  and
and  . In turn, the initialization of the target spin state at the input port can also be done with resonant microwave or radiofrequency field(s), upon shifting the transition frequency of the atom by a focused laser31,39, while the readout at the output port can be done by internal state selective fluorescence using the quantum gas microscope set-up40,41. Both the initialization and the readout can be accomplished during time intervals ∼10 μs—short compared with
. In turn, the initialization of the target spin state at the input port can also be done with resonant microwave or radiofrequency field(s), upon shifting the transition frequency of the atom by a focused laser31,39, while the readout at the output port can be done by internal state selective fluorescence using the quantum gas microscope set-up40,41. Both the initialization and the readout can be accomplished during time intervals ∼10 μs—short compared with  ms transfer time39.
ms transfer time39.
Data availability
The data that support the findings of this study are available from the corresponding authors upon request.
Additional information
How to cite this article: Marchukov, O. V. et al. Quantum spin transistor with a Heisenberg spin chain. Nat. Commun. 7, 13070 doi: 10.1038/ncomms13070 (2016).
References
Datta, S. & Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 56, 665–667 (1990).
Žutić, I., Fabian, J. & Das Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Awschalom, D. D., Bassett, L. C., Dzurak, A. S., Hu, E. L. & Petta, J. R. Quantum spintronics: engineering and manipulating atom-like spins in semiconductors. Science 339, 1174–1179 (2013).
Devoret, M. H. & Glattli, C. Single-electron transistors. Phys. World 11, 29 (1998).
Koenraad, P. M. & Flatté, M. E. Single dopants in semiconductors. Nat. Mater. 10, 91–100 (2011).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Leuenberger, M. N. & Loss, D. Quantum computing in molecular magnets. Nature 410, 789–793 (2001).
DiVincenzo, D. P., Bacon, D., Kempe, J., Burkard, G. & Whaley, K. B. Universal quantum computation with the exchange interaction. Nature 408, 339–342 (2000).
Levy, J. Universal quantum computation with spin-1/2 pairs and heisenberg exchange. Phys. Rev. Lett. 89, 147902 (2002).
Bose, S. Quantum communication through an unmodulated spin chain. Phys. Rev. Lett. 91, 207901 (2003).
Bose, S. Quantum communication through spin chain dynamics: an introductory overview. Contemp. Phys. 48, 13–30 (2007).
Nikolopoulos, G. M., Petrosyan, D. & Lambropoulos, P. Coherent electron wavepacket propagation and entanglement in array of coupled quantum dots. EPL 65, 297–303 (2004).
Christandl, M., Datta, N., Ekert, A. & Landahl, A. J. Perfect state transfer in quantum spin networks. Phys. Rev. Lett. 92, 187902 (2004).
Petrosyan, D., Nikolopoulos, G. M. & Lambropoulos, P. State transfer in static and dynamic spin chains with disorder. Phys. Rev. A 81, 042307 (2010).
Blundell, S. J. & Pratt, F. L. Organic and molecular magnets. J. Phys: Condens. Matter 16, R771–R828 (2004).
Zwanenburg, F. A. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961–1019 (2013).
Mourigal, M. et al. Fractional spinon excitations in the quantum Heisenberg antiferromagnetic chain. Nat. Phys. 9, 435–441 (2013).
Sahling, S. et al. Experimental realization of long-distance entanglement between spins in antiferromagnetic quantum spin chains. Nat. Phys. 11, 255–260 (2015).
Fazio, R. & van der Zant, H. Quantum phase transitions and vortex dynamics in superconducting networks. Phys. Rep. 355, 235–334 (2001).
Porras, D. & Cirac, J. I. Effective quantum spin systems with trapped ions. Phys. Rev. Lett. 92, 207901 (2004).
Blatt, R. & Roos, C. F. Quantum simulations with trapped ions. Nat. Phys. 8, 277–284 (2012).
Gambardella, P. et al. Ferromagnetism in one-dimensional monatomic metal chains. Nature 416, 301–304 (2002).
Hirjibehedin, C. F., Lutz, C. P. & Heinrich, A. J. Spin coupling in engineered atomic structures. Science 312, 1021–1024 (2006).
Khajetoorians, A. A., Wiebe, J., Chilian, B. & Wiesendanger, R. Realizing all-spin-based logic operations atom by atom. Science 332, 1062–1064 (2011).
Khajetoorians, A. A. et al. Atom-by-atom engineering and magnetometry of tailored nanomagnets. Nat. Phys. 8, 497–503 (2012).
Toskovic, R. et al. Atomic spin-chain realization of a model for quantum criticality. Nat. Phys. 12, 656–660 (2016).
Chumak, A. V., Serga, A. A. & Hillebrands, B. Magnon transistor for all-magnon data processing. Nat. Commun. 5, 4700 (2014).
Chumak, A. V., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Magnon spintronics. Nat. Phys. 11, 453–461 (2015).
Trotzky, S. et al. Time-resolved observation and control of superexchange interactions with ultracold atoms in optical lattices. Science 319, 295–299 (2008).
Fukuhara, T. et al. Quantum dynamics of a mobile spin impurity. Nat. Phys. 9, 235–241 (2013).
Fukuhara, T. et al. Microscopic observation of magnon bound states and their dynamics. Nature 502, 76–79 (2013).
Volosniev, A. G., Fedorov, D. V., Jensen, A. S., Valiente, M. & Zinner, N. T. Strongly interacting confined quantum systems in one dimension. Nat. Commun. 5, 5300 (2015).
Volosniev, A. G. et al. Engineering the dynamics of effective spin-chain models for strongly interacting atomic gases. Phys. Rev. A 91, 023620 (2015).
Deuretzbacher, F., Becker, D., Bjerlin, J., Reimann, S. M. & Santos, L. Quantum magnetism without lattices in strongly interacting one-dimensional spinor gases. Phys. Rev. A 90, 013611 (2014).
Levinsen, J., Massignan, P., Bruun, G. M. & Parish, M. M. Strong-coupling ansatz for the one-dimensional Fermi gas in a harmonic potential. Sci. Adv. 1, e1500197 (2015).
Murmann, S. et al. Antiferromagnetic heisenberg spin chain of a few cold atoms in a one-dimensional trap. Phys. Rev. Lett. 115, 215301 (2015).
Murmann, S. et al. Two fermions in a double well: exploring a fundamental building block of the hubbard model. Phys. Rev. Lett. 114, 080402 (2015).
Xia, T. et al. Randomized benchmarking of single-qubit gates in a 2d array of neutral-atom qubits. Phys. Rev. Lett. 114, 100503 (2015).
Bakr, W. S., Gillen, J. I., Peng, A., Fölling, S. & Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. Nature 462, 74–77 (2009).
Sherson, J. F. et al. Single-atom-resolved fluorescence imaging of an atomic Mott insulator. Nature 467, 68–72 (2010).
Acknowledgements
This work was funded in part by the Danish Council for Independent Research DFF Natural Sciences and the DFF Sapere Aude programme, and by the Carlsberg Foundation. A.G.V. acknowledges partial support by Helmholtz Association under contract HA216/EMMI. M.V. is funded by EPSRC EP/M024636/1. D.P. is grateful to the Aarhus Institute of Advanced Studies in Denmark for hospitality and support, and to the Alexander von Humboldt Foundation for support during his stay in Germany.
Author information
Authors and Affiliations
Contributions
O.V.M., A.G.V., M.V., D.P. and N.T.Z. devised the project. O.V.M. and A.G.V. developed the formalism under the supervision of D.P. and N.T.Z. The numerical calculations were carried out by O.V.M. The initial draft of the paper was written by O.V.M., N.T.Z. and D.P. All authors contributed to the revisions that led to the final version.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Notes 1-4 and Supplementary References (PDF 223 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Marchukov, O., Volosniev, A., Valiente, M. et al. Quantum spin transistor with a Heisenberg spin chain. Nat Commun 7, 13070 (2016). https://doi.org/10.1038/ncomms13070
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13070
This article is cited by
-
Continuum Soliton Chain Analog to Heisenberg Spin Chain System. Modulation Stability and Spectral Characteristics
International Journal of Theoretical Physics (2022)
-
Generation of spin currents by a temperature gradient in a two-terminal device
Communications Physics (2021)
-
Filtering spins by scattering from a lattice of point magnets
Communications Physics (2020)
-
Shortening time scale to reduce thermal effects in quantum transistors
Scientific Reports (2019)
-
Controlled state transfer in a Heisenberg spin chain by periodic drives
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.