Abstract
The tunnelling current in scanning tunnelling spectroscopy (STS) is typically and often implicitly modelled by a continuous and homogeneous charge flow. If the charging energy of a single-charge quantum sufficiently exceeds the thermal energy, however, the granularity of the current becomes non-negligible. In this quantum limit, the capacitance of the tunnel junction mediates an interaction of the tunnelling electrons with the surrounding electromagnetic environment and becomes a source of noise itself, which cannot be neglected in STS. Using a scanning tunnelling microscope operating at 15 mK, we show that we operate in this quantum limit, which determines the ultimate energy resolution in STS. The P(E)-theory describes the probability for a tunnelling electron to exchange energy with the environment and can be regarded as the energy resolution function. We experimentally demonstrate this effect with a superconducting aluminium tip and a superconducting aluminium sample, where it is most pronounced.
Similar content being viewed by others
Introduction
Scanning tunnelling spectroscopy has evolved into one of the most versatile tools to study the electronic structure in real space with atomic precision1,2,3. The differential conductance measured through the tunnelling contact directly accesses the local density of states of the sample. With the growing interest in phenomena with extremely sharp spectral features on smaller and smaller energy scales, the demand for higher and higher spectroscopic energy resolution increases. Examples are the Kondo effect4, Yu–Shiba–Rusinov states5,6, Majorana fermions7, or the Josephson effect8,9,10,11, just to name a few. Aside from the obvious strategy of lowering the temperature to increase the energy resolution12, superconducting tips have successfully been conducted to circumvent the broadening effects of the Fermi function in the tunnelling process and greatly improve the energy resolution6,13. However, at low temperature T, other energy scales such as the charging energy EC of the tunnel junction may substantially exceed the thermal energy kBT such that the granularity of the tunnelling current becomes non-negligible. The question arises whether the tunnelling process encompasses an intrinsic resolution limit, however small it may be, which cannot be overcome. In the following, we will show that the consequences of charge quantization ultimately pose a principal limit to the achievable energy resolution.
The principal properties of a tunnel junction can in many cases be satisfactorily described by a tunnelling resistance14 and the charge flow is commonly implicitly assumed to be continuous and homogeneous. However, at very low temperatures, the granularity of the tunnelling current resulting from charge quantization is not necessarily negligible. In this case, the tunnel junction also becomes a capacitor (see Fig. 1a) mediating an interaction of the tunnelling electrons with the surrounding electromagnetic environment15,16,17. This is the quantum limit, where electric charge and magnetic flux (phase) become dual variables (uncertainty principle) so that the charging energy cannot be neglected anymore. As a result, a tunnelling electron may exchange a photon with the surrounding environment, which is accompanied by a loss or gain in energy. This is schematically shown in Fig. 1b for a scanning tunnelling microscope (STM), where the electron tunnels from the tip to the sample and emits a photon to the environment. In addition, the thermal noise of the junction capacitance becomes appreciable for small capacitance values. These effects may be small, but they are non-negligible at low temperatures, especially in the context of ultimate energy resolution.
(a) Schematic drawing of an STM tunnel junction consisting of tip and sample. The equivalent circuit diagram is represented by a tunnelling resistor RT and the junction capacitance CJ. (b) Schematic energy diagram showing the energy loss of an electron tunnelling in an STM from the tip to the sample. Interacting with the surrounding environment, the electron loses energy according to the probability given by the P(E)-function. The FWHM is indicated with the values found in this work.
The so-called P(E)-theory quantifies the energy exchange with the environment, where the P(E)-function describes the probability of a tunnelling electron to emit or absorb a photon to or from the environment16,17,18,19,20. The P(E)-theory has already been successfully applied in many instances, where tunnelling electrons interact with the surrounding environment, which is modelled as an effective frequency-dependent electromagnetic impedance Z(ω). Examples include the Josephson effect in the charge tunnelling regime18,21, as well as the phenomenon of Coulomb blockade15,16,22,23. These examples refer to specific physical situations: tunnelling of Cooper pairs and tunnelling in a high-impedance environment ( , where
, where  is the resistance quantum), respectively. However, the P(E)-theory generally applies to inelastic charge transfer processes through tunnel junctions. Accordingly, Pekola et al.24 have very nicely described a contribution to the superconducting density of states (that is, the Dynes parameter) by environmentally assisted tunnelling through a normalconductor-insulator-superconductor junction. They did not though generalize their findings to the general properties of a tunnel junction.
is the resistance quantum), respectively. However, the P(E)-theory generally applies to inelastic charge transfer processes through tunnel junctions. Accordingly, Pekola et al.24 have very nicely described a contribution to the superconducting density of states (that is, the Dynes parameter) by environmentally assisted tunnelling through a normalconductor-insulator-superconductor junction. They did not though generalize their findings to the general properties of a tunnel junction.
Here, we show that the photon exchange of tunnelling electrons with the surrounding environment in conjunction with the capacitative junction noise represents a principal limit of the energy resolution ΔE in spectroscopic measurements using tunnel junctions (in our case leading to ΔE in the low μeV-range). In this regard, the P(E)-function represents the resolution function of a particular tunnel junction. Using an STM operating at 15 mK (ref. 25), we independently characterize the P(E)-function of a superconductor-vacuum–superconductor-tunnel junction through its direct relation with the Josephson effect. Subsequently, we demonstrate the impact of the P(E)-function on the tunnelling process by measuring the superconducting quasiparticle density of states of the same tunnel junction. We find excellent quantitative agreement of our spectra from different tunnel junctions with the model calculations including P(E)-theory. This leads us to conclude that the P(E)-function plays a ubiquitous role as a resolution function in the tunnelling process, in particular for energy scales at or below 1 meV.
Results
Theoretical modelling
To consider the effects of charge quantization in the tunnelling Hamiltonian, a charge transfer operator has to be included16. A detailed derivation can be found in ref. 19. The resulting tunnelling probability  from tip to sample as a function of applied bias voltage is given by refs 16, 26:
from tip to sample as a function of applied bias voltage is given by refs 16, 26:

Here, RT is the tunnelling resistance,  is the Fermi function, and nt, ns are the densities of states of tip and sample, respectively. By exchanging electrons and holes in equation (1), the other tunnelling direction (V) from sample to tip can be obtained. Equation (1) differs from the standard expression of the tunnelling probability by the convolution with the P(E)-function12,27. If we set P(E)=δ(E), which means that there is no energy exchange with the environment and no capacitative noise, the standard expression for the tunnelling current is recovered28. It can be clearly seen that the convolution with the P(E)-function results in a broadening of the spectral features in the density of states. The current I(V), which is measured through the tunnel junction as a function of applied bias voltage V, is the difference of the tunnelling probabilities in the forward
is the Fermi function, and nt, ns are the densities of states of tip and sample, respectively. By exchanging electrons and holes in equation (1), the other tunnelling direction (V) from sample to tip can be obtained. Equation (1) differs from the standard expression of the tunnelling probability by the convolution with the P(E)-function12,27. If we set P(E)=δ(E), which means that there is no energy exchange with the environment and no capacitative noise, the standard expression for the tunnelling current is recovered28. It can be clearly seen that the convolution with the P(E)-function results in a broadening of the spectral features in the density of states. The current I(V), which is measured through the tunnel junction as a function of applied bias voltage V, is the difference of the tunnelling probabilities in the forward  and the backward direction (V). The tunnelling current I(V) is then:
and the backward direction (V). The tunnelling current I(V) is then:

The effect of the capacitance in the tunnel junction and the interaction of the tunnelling electrons with the surrounding environmental impedance has been modelled within the framework of P(E)-theory, where the P(E)-function describes the probability for a tunnelling electron to exchange energy with the environment. It is commonly defined through the equilibrium phase correlation function J(t) as the Fourier transform of exp[J(t)] (refs 18, 19). To account for the different dissipation channels, we define J(t)=J0(t)+JN(t), where J0(t) describes the phase correlation of the environmental impedance and JN(t) captures the low frequency capacitative thermal noise in the junction. This allows us to calculate the P0(E)-function for the environmental impedance and the PN(E)-function for the capacitative noise separately. They can be combined to the total P(E)-function through a convolution (see ‘Methods’ section).
Because the correlation function is difficult to calculate directly, we choose an implicit definition for P0(E)20:

where the two functions I(E) and K(E,ω) are defined in the ‘Methods’ section. The P0(E)-function is parameterized by the temperature T, as well as the junction capacitance CJ, and the surrounding impedance Z(ω), which together form the total impedance:

In our STM, the tip acts as a monopole antenna, whose impedance can be modelled in analogy to an infinite transmission line impedance11,18. The fit parameters are the principal resonance frequency ω0 and a damping factor α. The d.c. resistance Z(0) is fixed at the vacuum impedance value of 376.73 Ω. The PN(E)-function is modelled by a normalized Gaussian of width  to account for the thermal voltage noise on the junction capacitor. Because both tip and sample are superconducting, we define the charging energy EC=Q2/2CJ using the charge of a Cooper pair (Q=2e)18, which makes it four times higher than the charging energy for a singly charged quasiparticle. Including the capacitative noise has proven essential in previous descriptions of the tunnelling current as well11.
to account for the thermal voltage noise on the junction capacitor. Because both tip and sample are superconducting, we define the charging energy EC=Q2/2CJ using the charge of a Cooper pair (Q=2e)18, which makes it four times higher than the charging energy for a singly charged quasiparticle. Including the capacitative noise has proven essential in previous descriptions of the tunnelling current as well11.
Josephson tunnelling in the dynamical Coulomb blockade regime
The experiments were carried out in an STM operating at a base temperature of 15 mK (ref. 25). We use an Al tip and an Al(100) sample29,30, which is superconducting at 15 mK (transition temperature TC=1.1 K). Aluminium has been shown to exhibit minimal intrinsic broadening due to depairing resulting in sharp coherence peaks31, which is why it is an excellent material for demonstrating the broadening effects in a tunnel junction, as we will show in the following. We used two different tip wires with diameters of 0.25 and 1 mm (tip 1 and tip 2, respectively) expecting different junction capacitances CJ.
To demonstrate the influence of the P(E)-function on density of states measurements, we have to independently determine the P(E)-function from a separate measurement. Since every tip in an STM is slightly different, we have to determine the P(E)-function for every tip separately. As both tip and sample are superconducting at 15 mK, the most straightforward way to experimentally determine the P(E)-function is through the Josephson effect. We have to use the P(E)-theory to describe the Josephson effect rather than the Ivanchenko–Zil'berman (IZ) model, which has been used in STM measurements before, because the IZ model is only valid in the classical phase diffusion limit ( )18,32. In the case of a simple ohmic impedance (and only then), a capacitative element renormalizes the Josephson energy, so that the IZ model can still be used3334. This is clearly not the case here. Furthermore, as has been shown before, the environmental impedance in our experiment exhibits resonances and cannot be approximated by the generic impedance in the IZ model11,35. In the sequential charge tunnelling regime, where the charging energy EC is larger than the Josephson energy EJ (which is commonly the case in a standard STM setup), the current–voltage characteristics is given by ref. 18:
)18,32. In the case of a simple ohmic impedance (and only then), a capacitative element renormalizes the Josephson energy, so that the IZ model can still be used3334. This is clearly not the case here. Furthermore, as has been shown before, the environmental impedance in our experiment exhibits resonances and cannot be approximated by the generic impedance in the IZ model11,35. In the sequential charge tunnelling regime, where the charging energy EC is larger than the Josephson energy EJ (which is commonly the case in a standard STM setup), the current–voltage characteristics is given by ref. 18:

The Josephson energy EJ, can be regarded as a scaling parameter here36. In this sense, the I(V) measurement of the Josephson effect is a direct measure of the P(E)-function18,19.
We have measured the I(V)-characteristics of the Josephson effect for two different aluminium tips, which are shown in Fig. 2. The tunnelling conditions were such that for both tips the current setpoint was 5 nA at a voltage of 1 and 2 meV for tip 1 and 2, respectively. For better comparison, the current was divided by  . The general features of the Josephson effect in the sequential charge tunnelling regime are visible, however, the peak in Fig. 2b is somewhat higher and sharper than in panel (a). In addition, the spectrum in panel (a) shows a broad peak of the principal antenna resonance ω0. The fits using equation (5) are shown as black lines (see Supplementary Note 1). They agree well with the measured data. The most significant difference between the two tunnel junctions is that the junction in the Fig. 2a has a capacitance of CJ=3.5±0.2 fF, while in Fig. 2b the capacitance is CJ=7.0±0.1 fF, which can be traced back to the different wire diameters (see ‘Methods’ section). The lower the junction capacitance value CJ is, the more sensitive the junction will be to the environment Z(ω) (cf. equation (8)).
. The general features of the Josephson effect in the sequential charge tunnelling regime are visible, however, the peak in Fig. 2b is somewhat higher and sharper than in panel (a). In addition, the spectrum in panel (a) shows a broad peak of the principal antenna resonance ω0. The fits using equation (5) are shown as black lines (see Supplementary Note 1). They agree well with the measured data. The most significant difference between the two tunnel junctions is that the junction in the Fig. 2a has a capacitance of CJ=3.5±0.2 fF, while in Fig. 2b the capacitance is CJ=7.0±0.1 fF, which can be traced back to the different wire diameters (see ‘Methods’ section). The lower the junction capacitance value CJ is, the more sensitive the junction will be to the environment Z(ω) (cf. equation (8)).
I(V)-characteristics of the Josephson effect for two different Al tips on an Al(100) sample. The tunnel junctions in (a) and (b) have a capacitance of 3.5 fF and 7 fF, respectively, which means that the tunnel junction in (a) is more sensitive to the surrounding environment. Therefore, the principal impedance resonance ω0 is visible in (a) and not in (b). The fit using P(E)-theory (black lines) is in excellent agreement with the data. The P(E)-functions extracted from the fits in (a) and (b) are shown on a linear scale in (c) and on a logarithmic scale in (d). The asymmetry of the P(E)-function is clearly visible.
The actual shape of the P(E)-function for the two tips is shown in Fig. 2c and on a semi-log scale in (d). The full-width at half maximum (FWHM) for tip 1 and 2 is 77.2 μeV and 65.4 μeV, respectively, which will have a non-negligible effect on the superconducting density of states. In addition, the P0(E)-function obeys the detailed balance symmetry20,  , which makes the function inherently asymmetric as can be clearly seen in Fig. 2d even after the convolution with the capacitative noise. With the well-defined P(E)-function, we can look at its impact on the details of a quasiparticle spectrum.
, which makes the function inherently asymmetric as can be clearly seen in Fig. 2d even after the convolution with the capacitative noise. With the well-defined P(E)-function, we can look at its impact on the details of a quasiparticle spectrum.
Charge quantization effects in quasiparticle spectra
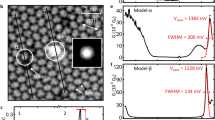
The differential conductance dI/dV spectra measured with the two tips as a function of bias voltage V are shown in Fig. 3. The lock-in modulation for the spectra was 10 μeV (peak-to-peak) at 724 Hz. Because both the tip and the sample are superconducting, the apparent gap in the spectrum has a width of 2(Δt+Δs). The tip gap Δt can be slightly smaller than the bulk value of 180 μeV. The most noticeable difference between the two spectra is the height of the coherence peaks. We fit the two spectra with the differential conductance model obtained from the derivative of equation (2) in combination with equation (1). For the superconducting density of states in tip nt and sample ns, we use the simple BCS model37, explicitly neglecting any intrinsic broadening (for example, Dynes parameter Γ (ref. 38)):
Differential conductance spectra of the superconducting densities of states for the two different Al tips on an Al(100) sample (the tip wire diameters are 0.25mm in (a) and 1mm in (b)). To suppress subgap features, we have measured at low transmission (stabilization at 2 meV and 50 pA). The fits are shown as black lines with excellent agreement. The superconducting density of states of both tip and sample was modeled by the simple Bardee–Cooper–Schrieffer (BCS)-model without any additional broadening parameters.

For the P(E)-function we use the same values that have been obtained from the fit to the data in Fig. 2, which means that the number of fit parameters is reduced to the value of the superconducting gap Δ and an overall scaling factor including the tunnelling resistance RT. We find excellent agreement for both spectra using the corresponding P(E)-function and with gap values of Δt=160±2 μeV for tip 1 and Δt=180±2 μeV for tip 2. The sample gap is set to the bulk value Δs=180 μeV. In both cases, the height and the shape of the coherence peaks are quantitatively well reproduced.
By contrast, disregarding the P(E)-function and fitting the spectra in Fig. 3 with the Dynes equation38 to account for the broadening, does not give a satisfactory fit at all (see Supplementary Note 2 and Supplementary Figure 1). The height reduction in the coherence peaks has to be absorbed into the empirical broadening parameter Γ. This leads to the accumulation of quasiparticle spectral weight inside the gap, which is not observed experimentally. In fact, as outlined in the ‘Methods’ section, the Coulomb dip found in the normal conducting state of tip and sample strongly supports our P(E)-analysis. Since it is well described by the same P(E)-function as for the quasiparticle spectrum and the Josephson spectrum, we attribute the reduction of the singularities to sharp peaks to the P(E)-function broadening.
Discussion
According to the P(E)-theory, the exchange of energy with the environment during the tunnelling process should be an ubiquitous phenomenon16. In the majority of cases, it has been discussed in the context of dynamical Coulomb blockade (DCB)15,16,22,23 as well as the Josephson effect in the sequential charge tunnelling regime17,18,21. While in these cases, the role of the P(E)-theory is obvious, its role as a resolution function in every tunnelling spectrum is more subtle, but non-negligible, as we will show in the following. Neglecting the asymmetric shape for a moment and looking at the general broadening effect of the P(E)-function, we find that the FWHM of the P(E)-function is dominated by the capacitative noise and is essentially determined by the junction capacitance CJ as well as the temperature T (see also Supplementary Note 3).
The FWHM of the P(E)-function for typical low temperatures (0.01–5 K) and capacitances (1–50 fF) is shown in Fig. 4. For comparison, the conventional thermal broadening ΔEtherm of differential conductance spectra in the STM due to the Fermi function is also shown as a black line (ΔEtherm=3.5 kBT). While the thermal Fermi function broadening depends linearly on temperature, we find an overall empirical relation for the effective energy resolution due to P(E)-broadening, which is a function of temperature and capacitance  . The coefficient γ has an average value of γ=2.45±0.1, keeping in mind that the capacitative noise is the dominant contribution to the FWHM. The P0(E)-function changes the coefficient γ slightly depending on the actual values of the parameters. This means that for low-enough temperature, the P(E)-broadening will eventually be the dominant contribution to the resolution limit, regardless of whether the tip and/or sample are superconducting or not. We note that this empirical equation holds for capacitive noise from Cooper pairs. For noise from quasiparticles, we expect the P(E)-broadening to be reduced by about one half. At or below 1 K, the P(E)-broadening definitely has to be taken into account when optimizing the energy resolution. The optimizing strategy will be to increase the junction capacitance by appropriate ex situ tip shaping on a macroscopic scale (up to mm-scale). Increasing the junction capacitance will increase the crosstalk between tip and sample, so that a trade-off between energy resolution and STM performance will have to be made.
. The coefficient γ has an average value of γ=2.45±0.1, keeping in mind that the capacitative noise is the dominant contribution to the FWHM. The P0(E)-function changes the coefficient γ slightly depending on the actual values of the parameters. This means that for low-enough temperature, the P(E)-broadening will eventually be the dominant contribution to the resolution limit, regardless of whether the tip and/or sample are superconducting or not. We note that this empirical equation holds for capacitive noise from Cooper pairs. For noise from quasiparticles, we expect the P(E)-broadening to be reduced by about one half. At or below 1 K, the P(E)-broadening definitely has to be taken into account when optimizing the energy resolution. The optimizing strategy will be to increase the junction capacitance by appropriate ex situ tip shaping on a macroscopic scale (up to mm-scale). Increasing the junction capacitance will increase the crosstalk between tip and sample, so that a trade-off between energy resolution and STM performance will have to be made.
Energy broadening due to P(E)-broadening from the environment in comparison to thermal broadening from the Fermi functions as a function of temperature. The P(E)-broadening is shown for typical junction capacitances that can be found in an STM tunnel junction (see ‘Methods’ Section). For the total energy broadening and hence the resolution limit both contributions have to be combined.
Due to the asymmetry of the P(E)-function, the spectral features in the density of states will not only be broadened, but may also change shape, which can have a strong influence on the interpretation of experimental data. The asymmetry evens out for higher temperatures, but at low temperatures, it has to be considered as can be seen in the fits of the differential conductance spectra in Fig. 3. If a symmetric broadening had been sufficient to fit these spectra, a Dynes fit would likely have sufficed. We expect the P(E)-broadening to be most significant on intrinsically sharp spectral features, such as coherence peaks of a superconducting gap. In addition, sharp Kondo peaks with a low Kondo temperature on the order of 1 K may show an effectively higher Kondo temperature when the P(E)-broadening is not taken into account. Also, Yu–Shiba–Rusinov states, which have an intrinsically δ-like spectral appearance39, will be strongly influenced by P(E)-broadening.
In summary, we have shown that the interaction of tunnelling electrons with the environmental impedance as well as the capacitative junction noise limit the effective energy resolution in spectroscopic measurements of the differential conductance with the STM. The P(E)-function that models the energy exchange with the electromagnetic environment combined with the capacitative noise is the energy resolution function of the tunnel junction. The effect of P(E)-broadening becomes dominant at or below 1 K and has to be taken into account when optimizing the energy resolution. In this regime, the quantum nature of the tunnelling process becomes evident, there is virtually no elastic tunnelling in experiments, and the surrounding electromagnetic environment has to be taken into account.
Methods
Sample preparation
The sample that was used was an Al(100) single crystal and the tip was an Al wire of 99.9999% purity. The sample was sputtered (Ar+ ions at 500 eV) and annealed in ultrahigh vacuum (low 10−10 mbar range) in several cycles, while the tip was cut in air, transferred in vacuum and then sputtered (Ar+ ions at 500 eV) to remove the native oxide. With a superconducting transition temperature TC=1.1 K both tip and sample are superconducting at 15 mK with a fully open gap. The quasiparticle density of states of aluminium in the superconducting state has a very Bardeen–Cooper–Schrieffer (BCS)-like character with minimal intrinsic broadening31, which is why aluminium is an excellent material for demonstrating the broadening effects in a tunnel junction.
The dynamical Coulomb blockade regime
We assume a sequential tunnelling regime, where the system, including the environment, is relaxed before the next quasiparticle or Cooper pair tunnels. To support our treatment of inelastic Cooper pair/quasiparticle tunnelling in the main text, we here show data for the normal conducting regime. Accordingly, DCB should then induce a characteristic dip in the differential conductance around zero voltage. This is indeed found in Fig. 5a, which shows the differential conductance spectrum taken with the Al tip and the Al sample in the normal conducting state in a 10 mT magnetic field. The spectrum clearly shows a conductance dip by about 8% demonstrating a DCB in our system. This dip is clear evidence that the consequences of charge quantization cannot be neglected in our operating regime. Consequently, we have to take the effects of the tunnelling capacitance into account and conduct P(E)-theory to describe our data21. The spectra in Fig. 5b,c show the quasiparticle spectrum in the superconducting state (at 0 mT) and the Josephson effect, respectively. Both of these spectra were fitted with the same P(E)-function as in Fig. 5a having a capacitance CJ=7 fF (tip wire with 1 mm diameter), a resonance energy  and a damping factor α=0.75 (the details of these parameters are described below). The fitted temperature was 100 mK. For the spectrum in Fig. 5a, we used the charging energy EC for quasiparticles, because both tip and sample are in the normal conducting state. For the spectrum in Fig. 5b,c, we used the charging energy for Cooper pairs.
and a damping factor α=0.75 (the details of these parameters are described below). The fitted temperature was 100 mK. For the spectrum in Fig. 5a, we used the charging energy EC for quasiparticles, because both tip and sample are in the normal conducting state. For the spectrum in Fig. 5b,c, we used the charging energy for Cooper pairs.
(a) Differential conductance spectrum in the normal state after applying a 10 mT magnetic field to quench superconductivity in the tip and the sample. The conductance dip at zero bias clearly indicates a DCB as a result of charge quantization effects. The quasiparticle spectrum of the superconducting Al tip and sample in (b) and the Josephson spectrum in (c) were fitted with the same P(E)-function as used in (a).
Modelling the superconducting gap
We model the superconducting gap of aluminium with the simple BCS model because we work with high purity tip and sample material, so that we assume that there is negligible depairing due to impurities in the material. Further, the tip is solid aluminium wire, and we have not observed any indications of confinement effects. As such, there is a priori no real justification to describe the superconducting gap with Maki's equation or the Usadel equation40,41, although the functions may give a satisfactory fit. Conducting P(E)-theory gives an overall consistent picture and describes the superconduting quaisparticle spectrum with the simplest BCS model demonstrating that P(E)-broadening is the dominating broadening mechanism in our case.
Modelling the environmental impedance
In our STM the surrounding impedance that contributes to the P(E)-function is the vacuum as well as the tip acting as a monopole antenna with a corresponding resonance spectrum that depends on the length of the tip11. Approximating the resonance spectrum by an infinite transmission line impedance11,18, we find an analytic expression for the impedance Z(ω):

where Renv is the effective d.c. resistance of the environmental impedance, α is an effective damping parameter and ω0 is the frequency of the principal resonance. The parameter Renv is set to the vacuum impedance of 376.73 Ω. The fit parameters for this impedance are α and ω0.
The total impedance ZT(ω) takes into account the capacitance CJ in the tunnel junction as well:

Here, the parameter CJ is also a fit parameter.
Calculating the P(E)-function
The P(E)-function is commonly defined through the equilibrium phase correlation function J(t) through18:

We regard the energy exchange with the environmental impedance and the capacitative noise from the tunnel junction as two independent processes, which allows us to separate the correlation function as:

where J0(t) is the phase correlation function from the environmental impedance and JN(t) is due to the capacitative junction noise. We can then calculate the corresponding probability functions separately, where P0(E) is the probability due to the interaction with the environmental impedance and PN(E) is due to the capacitative noise. Exploiting the convolution theorem, we can calculate the total P(E)-function through a convolution:

For the calculation of the P0(E)-function for the environmental impedance, we follow the implementation given in ref. 20. The P0(E)-function is calculated through an indirect definition within an integral equation:

where K(E,ω) is the integral kernel. The inhomogeneity I(E) is defined as:

with

where  , T is the temperature, and RQ=h/(2e2) is the resistance quantum. The integral kernel K(E,ω) is defined as:
, T is the temperature, and RQ=h/(2e2) is the resistance quantum. The integral kernel K(E,ω) is defined as:

with the functions k(ω) and κ(ω) being:


The Matsubara frequencies vn are defined as  . Using the inhomogeneity I(E) as a starting value for the P0(E)-function calculation, the integral equation in equation (12) can be solved self-consistently. Convergence is usually reached within a few iterations. Treating the integral as a convolution, the calculation can be done very efficiently numerically. Care should be taken to extend the integral range to sufficiently large energies, while at the same time having a high enough numerical point density. Other than the impedance ZT(ω), the temperature T is a fit parameter in this part of the P(E)-function calculation.
. Using the inhomogeneity I(E) as a starting value for the P0(E)-function calculation, the integral equation in equation (12) can be solved self-consistently. Convergence is usually reached within a few iterations. Treating the integral as a convolution, the calculation can be done very efficiently numerically. Care should be taken to extend the integral range to sufficiently large energies, while at the same time having a high enough numerical point density. Other than the impedance ZT(ω), the temperature T is a fit parameter in this part of the P(E)-function calculation.
The PN(E)-function for the thermal capacitative noise of the tunnel junction has proven a non-negligible part of the total P(E)-function. The low frequency capacitative noise PN(E) is modelled by a Gaussian18:

where EC=Q2/2CJ is the charging energy for Cooper pairs (Q=2e). The PN(E)-function does not introduce any new fit parameters as the junction capacitance CJ as well as the temperature T are already defined in the P0(E)-function.
Estimating the junction capacitance
The capacitance of the tunnel junction cannot be easily calculated as the details of the tip shape of the apex are unknown. However, it is possible to estimate the contributions to the junction capacitance from a simple model that can be calculated analytically. Assuming a conical tip that touches a flat sample in one point (see Fig. 6), we can calculate the junction capacitance CJ using spherical coordinates:

This model shows that for the junction capacitance the full diameter d of the tip has to be considered. For a tip wire diameter d of 0.5 mm and an opening angle α of 60°, we calculate a junction capacitance of about 21 fF. In the experiment we have used wire diameters of 0.25 mm (tip 1) and 1 mm (tip 2), with junction capacitances of 3.5 and 7 fF, respectively. Considering the crudeness of the model, we find good agreement between experiment and calculation.
From the total impedance ZT(ω) in equation (8), we find that the larger the junction capacitance CJ, the less sensitive the junction will be to the environment, the smaller the capacitative noise will be, and, correspondingly, the better the energy resolution will be. Thus, the diameter of the tip plays a crucial role. The length of the tip will essentially determine the position of the antenna resonances, which is less crucial to the energy resolution.
Data availability
The authors declare that the data supporting the findings of this study are available within the article and its supplementary information.
Additional information
How to cite this article: Ast, C. R. et al. Sensing the quantum limit in scanning tunnelling spectroscopy. Nat. Commun. 7, 13009 doi: 10.1038/ncomms13009 (2016).
References
Wiesendanger, R. Spin mapping at the nanoscale and atomic scale. Rev. Mod. Phys. 81, 1495 (2009).
Bode, M. Spin-polarized scanning tunnelling microscopy. Rep. Prog. Phys. 66, 523–582 (2003).
Leemput, L. E. C. v. d. & Kempen, H. v. Scanning tunnelling microscopy. Rep. Prog. Phys. 55, 1165 (1992).
Zhang, Y.-h. et al. Temperature and magnetic field dependence of a Kondo system in the weak coupling regime. Nat. Commun. 4, 2110 (2013).
Yazdani, A., Jones, B. A., Lutz, C. P., Crommie, M. F. & Eigler, D. M. Probing the local effects of magnetic impurities on superconductivity. Science 275, 1767–1770 (1997).
Franke, K. J., Schulze, G. & Pascual, J. I. Competition of superconducting phenomena and kondo screening at the nanoscale. Science 332, 940–944 (2011).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602–607 (2014).
Naaman, O., Teizer, W. & Dynes, R. C. Fluctuation dominated Josephson tunneling with a scanning tunneling microscope. Phys. Rev. Lett. 87, 097004 (2001).
Kimura, H., Barber, R. P., Ono, S., Ando, Y. & Dynes, R. C. Josephson scanning tunneling microscopy: a local and direct probe of the superconducting order parameter. Phys. Rev. B 80, 144506 (2009).
Rodrigo, J. G., Crespo, V. & Vieira, S. Josephson current at atomic scale: tunneling and nanocontacts using a STM. Phys. C 437–438, 270–273 (2006).
Jäck, B. et al. A nanoscale gigahertz source realized with Josephson scanning tunneling microscopy. Appl. Phys. Lett. 106, 013109 (2015).
Tersoff, J. & Hamann, D. R. Theory of the scanning tunneling microscope. Phys. Rev. B 31, 805–813 (1985).
Pan, S. H., Hudson, E. W. & Davis, J. C. Vacuum tunneling of superconducting quasiparticles from atomically sharp scanning tunneling microscope tips. Appl. Phys. Lett. 73, 2992–2994 (1998).
Chen, C. J. Introduction To Scanning Tunneling Microscopy Oxford Univ. Press (2008).
Delsing, P., Likharev, K. K., Kuzmin, L. S. & Claeson, T. Effect of high-frequency electrodynamic environment on the single-electron tunneling in ultrasmall junctions. Phys. Rev. Lett. 63, 1180–1183 (1989).
Devoret, M. H. et al. Effect of the electromagnetic environment on the coulomb blockade in ultrasmall tunnel junctions. Phys. Rev. Lett. 64, 1824 (1990).
Averin, D., Nazarov, Y. & Odintsov, A. Incoherent tunneling of the cooper pairs and magnetic flux quanta in ultrasmall Josephson junctions. Phys. B 165–166, 945 (1990).
Ingold, G., Grabert, H. & Eberhardt, U. Cooper-pair current through ultrasmall Josephson junctions. Phys. Rev. B 50, 395 (1994).
Ingold, G.-L. & Nazarov, Y. V. Single Charge Tunneling, chap. Charge Tunneling Rates in Ultrasmall Junctions Plenum Press (1992).
Ingold, G.-L. & Grabert, H. Finite-temperature current-voltage characteristics of ultrasmall tunnel junctions. Europhys. Lett. 14, 371 (1991).
Hofheinz, M. et al. Bright side of the Coulomb blockade. Phys. Rev. Lett. 106, 217005 (2011).
Brun, C. et al. Dynamical Coulomb blockade observed in nanosized electrical contacts. Phys. Rev. Lett. 108, 126802 (2012).
Serrier-Garcia, L. et al. Scanning tunneling spectroscopy study of the proximity effect in a disordered two-dimensional metal. Phys. Rev. Lett. 110, 157003 (2013).
Pekola, J. P. et al. Environment-assisted tunneling as an origin of the dynes density of states. Phys. Rev. Lett. 105, 026803 (2010).
Assig, M. et al. A 10 mK scanning tunneling microscope operating in ultra high vacuum and high magnetic fields. Rev. Sci. Inst 84, 033903 (2013).
Odintsov, A. Effect of dissipation on the characteristics of small-area tunnel junctions: application of the polaron model. Sov. Phys. JETP 67, 1265 (1988) (Russian original - ZhETF, 94, 312, 1988)).
Bardeen, J. Tunnelling from a many-particle point of view. Phys. Rev. Lett. 6, 57–59 (1961).
Chen, C. J. Theory of scanning tunneling spectroscopy. J. Vac. Sci. Technol 6, 319–322 (1988).
Guillamon, I., Suderow, H., Vieira, S. & Rodiere, P. Scanning tunneling spectroscopy with superconducting tips of Al. Phys. C 468, 537–542 (2008).
Rodrigo, J. G., Suderow, H. & Vieira, S. On the use of STM superconducting tips at very low temperatures. Eur. Phys. J. B 40, 483–488 (2004).
Giaever, I., Hart, H. R. & Megerle, K. Tunneling into superconductors at temperatures below 1°K. Phys. Rev. 126, 941–948 (1962).
Ivanchenko, Y. M. & Zil'berman, L. A. The Josephson effect in small tunnel contacts. Sov. Phys. JETP 28, 1272 (1969).
Grabert, H., Ingold, G.-L. & Paul, B. Phase diffusion and charging effects in Josephson junctions. Europhys. Lett. 44, 360–366 (1998).
Ankerhold, J. et al. Overdamped quantum phase diffusion and charging effects in Josephson junctions. Europhys. Lett. 67, 280 (2004).
Jäck, B. et al. Critical Josephson current in the dynamical Coulomb blockade regime. Phys. Rev. B 93, 020504 (2016).
Ambegaokar, V. & Baratoff, A. Tunneling between superconductors. Phys. Rev. Lett. 10, 486–489 (1963).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957).
Dynes, R. C., Narayanamurti, V. & Garno, J. P. Direct measurement of quasiparticle-lifetime broadening in a strong-coupled superconductor. Phys. Rev. Lett. 41, 1509–1512 (1978).
Salkola, M. I., Balatsky, A. V. & Schrieffer, J. R. Spectral properties of quasiparticle excitations induced by magnetic moments in superconductors. Phys. Rev. B 55, 12648–12661 (1997).
Worledge, D. & Geballe, T. Maki analysis of spin-polarized tunneling in an oxide ferromagnet. Phys. Rev. B 62, 447–451 (2000).
Usadel, K. D. Generalized diffusion equation for superconducting alloys. Phys. Rev. Lett. 25, 507–509 (1970).
Author information
Authors and Affiliations
Contributions
C.R.A., B.J., J.A. and K.K. initiated the project. C.R.A. analyzed the data, interpreted results, wrote the manuscript and did the theoretical calculations with the help of J.A. and B.J. B.J. and J.S. measured the data with support from M.El. and M.Et. All authors contributed to the discussion and to the completion of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1, Supplementary Notes 1-3 and Supplementary References. (PDF 135 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ast, C., Jäck, B., Senkpiel, J. et al. Sensing the quantum limit in scanning tunnelling spectroscopy. Nat Commun 7, 13009 (2016). https://doi.org/10.1038/ncomms13009
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13009
This article is cited by
-
Determining the temperature of a millikelvin scanning tunnelling microscope junction
Communications Physics (2023)
-
Superconducting quantum interference at the atomic scale
Nature Physics (2022)
-
Correlating Josephson supercurrents and Shiba states in quantum spins unconventionally coupled to superconductors
Nature Communications (2021)
-
Light–matter interaction at atomic scales
Nature Reviews Physics (2021)
-
Single channel Josephson effect in a high transmission atomic contact
Communications Physics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.