Abstract
Topological quantum materials represent a new class of matter with both exotic physical phenomena and novel application potentials. Many Heusler compounds, which exhibit rich emergent properties such as unusual magnetism, superconductivity and heavy fermion behaviour, have been predicted to host non-trivial topological electronic structures. The coexistence of topological order and other unusual properties makes Heusler materials ideal platform to search for new topological quantum phases (such as quantum anomalous Hall insulator and topological superconductor). By carrying out angle-resolved photoemission spectroscopy and ab initio calculations on rare-earth half-Heusler compounds LnPtBi (Ln=Lu, Y), we directly observe the unusual topological surface states on these materials, establishing them as first members with non-trivial topological electronic structure in this class of materials. Moreover, as LnPtBi compounds are non-centrosymmetric superconductors, our discovery further highlights them as promising candidates of topological superconductors.
Similar content being viewed by others
Introduction
Topological quantum materials, a new class of matter with non-trivial topological electronic structures, has become one of the most intensively studied fields in physics and material science due to their rich scientific significance and broad application potentials1,2. With the worldwide effort, there have been numerous materials predicted and experimentally confirmed as topologically non-trivial matter (including topological insulators3,4, topological crystalline insulators5,6 and three-dimensional (3D) topological Dirac and Weyl semimetals7,8,9,10,11). However, there is a big family of materials—the Heusler compounds—although being theoretically predicted to be topologically non-trivial back in 2010 (refs 12, 13, 14), the non-trivial topological nature has never been experimentally confirmed up to date.
The ternary semiconducting Heusler compounds, with their great diversity (∼500 members, >200 are semiconductors) give us the opportunity to search for optimized parameters (for example, spin–orbit coupling (SOC) strength, gap size and so on) across different compounds—which is critical not only for realizing the topological order and investigating the topological phase transitions12, but also for designing realistic applications. In addition, among the wealth of Heusler compounds, many (especially those containing rare-earth elements with strongly correlated f electrons) exhibit rich interesting ground state properties, such as magnetism15,16, superconductivity17,18,19 or heavy fermion behaviour20. The interplay between these properties and the topological order makes Heusler compounds ideal platforms for the realization of novel topological effects (for example, exotic particles including image monopole effect and axions and so on), new topological phases (for example, topological superconductors21,22) and broad applications (see ref. 23 for a review).
Rare-earth half-Heusler compounds LnPtBi (Ln=Y, La and Lu) represent a model system recently proposed that can possess topological orders with non-trivial topological surface states (TSSs) and large band inversion12,24. Moreover, due to the lack of the inversion symmetry in their crystal structure, non-centrosymmetric superconducting LnPtBi compounds (Tc=0.717, 0.918 and 1.0 K19 for Ln=Y, La and Lu, respectively) may also host unconventional cooper pairs with mixed parity, making them promising candidates for the investigation of topological superconductivity and the search for Majorana fermions25.
However, despite the great interests and intensive research efforts in both theoretical12,13,26 and experimental27,28,29 investigations, the topological nature on LnPtBi remains elusive. A previous angle-resolved photoemission spectroscopy (ARPES) study has reported metallic surface states27 with apparently different dispersion shapes and Fermi surface (FS) crossing numbers from the predicted TSSs in LnPtBi compounds12,13, making the topological nature of LnPtBi controversial.
In this work, by carefully performing comprehensive ARPES measurements and ab initio calculations, we resolve this unsettled question. We observe the non-trivial TSSs with linear dispersions in half-Heusler compounds LuPtBi and YPtBi (on the Bi-and Y-terminated (111) surface, respectively); and remarkably, in contrast to many topological insulators that have TSSs inside their bulk gap1,3,30, the TSSs in LnPtBi show their unusual robustness by lying well below the Fermi energy (EF) and strongly overlapping with the bulk valence bands (similar to those in HgTe31,32,33). In addition to the TSSs, we also observe numerous metallic surface states crossing the EF with large Rashba splitting, which not only makes them promising compounds for spintronic application, but also provides the possibility to mediate topologically non-trivial superconductivity in the superconducting phase of these compounds.
Results
Basic physical properties of LnPtBi
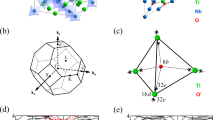
A crystallographic unit cell of LnPtBi is shown in Fig. 1a, which comprises of a zinc-blend unit cell from Bi and Pt atoms and rocksalt unit cell from Bi and Ln. For ARPES measurements, the LnPtBi single crystals were cleaved in situ in the ultra-high vacuum measurement chamber, resulting in either (111) or (001) surfaces. The unit cell along the (111) cleavage surface is illustrated in Fig. 1b and the corresponding hexagonal surface Brillouin zone (BZ) is shown in Fig. 1d, which could be viewed as the projection of the bulk BZ (Fig. 1c) of LnPtBi along the [111] direction (Fig. 1d).
(a) Crystal structure of half-Heusler alloy LnPtBi crystal shows a composite of zinc-blend and rocksalt lattices. (b) Unit cell of LnPtBi at the (111) cleavage surface shows the stacking of triangular Ln, Pt and Bi layers. a0 is the in-plane lattice constant of the (111) surface unit cell. (c) Bulk BZ of LnPtBi with high symmetry points labelled. Arrows and shaded surfaces indicate the projection to [100], [010] and [001] directions. (d) Surface BZ in the [111] direction with the high symmetry points labelled. (e) Core level photoemission spectrum on LuPtBi (111) and (001) surfaces clearly shows the characteristic Lu 4f and Bi 5d doublets. These spectra are measured with 75 and 215 eV photons, respectively. (f) Broad FS map of LuPtBi covering five BZs, confirming the shape and size of the surface BZ (overlaid yellow hexagons) on the (111) cleave plane. The uneven intensity of the FS at different BZs results from the matrix element effect.
The unit cell along the [111] direction consists of alternating Ln, Pt and Bi layers (Fig. 1b). As there are fewer chemical bonds to break between Ln and Bi layer (two comparing to three between Ln and Pt or Pt and Bi layers) and the Ln–Bi layer distance is twice as large as the Ln–Pt or Pt–Bi layer spacing (see Fig. 1b), it is more energetically favourable to cleave the material between Ln and Bi layers. In the discussion of the main text, we will focus on the electronic structure of Bi-terminated (111) surface LuPtBi and Y-terminated (111) surface of YPtBi. ARPES results (as well as ab initio calculations) along (001) cleavage surfaces of LuPtBi and YPtBi are presented in Supplementary Information.
The core level photoemission spectra of LuPtBi is shown in Fig. 1e, from which the characteristic Bi 5d and Lu 4f doublets are clearly observed. The large spectral weight of Bi peaks over the Lu peaks in the (111) surface clearly indicates its Bi termination. The broad area FS mapping covering multiple BZs in Fig. 1f also illustrates the hexagonal symmetry (with the correct lattice parameters) resulting from the (111) cleaved surface.
General electronic structure of LuPtBi (111) surface
In Fig. 2, detailed electronic structures of LuPtBi within a surface BZ are illustrated. From the FS maps (Fig. 2a–c) and 3D spectral intensity plots (Fig. 2d,e) around both the  point and BZ boundary (
point and BZ boundary ( and
and  points), there are clearly multiple bands crossing EF, forming a twin hexagonal hole pockets at
points), there are clearly multiple bands crossing EF, forming a twin hexagonal hole pockets at  and complex electron pockets at
and complex electron pockets at  and
and  , both of which show clear Rashba splitting. Around
, both of which show clear Rashba splitting. Around  , there is another pair of double Λ shape hole bands just below EF. These features broadly agree with the previous ARPES report27 (also see Supplementary Figs 1 and 2 and Supplementary Note 1 for the detailed discussions on the features near
, there is another pair of double Λ shape hole bands just below EF. These features broadly agree with the previous ARPES report27 (also see Supplementary Figs 1 and 2 and Supplementary Note 1 for the detailed discussions on the features near  ). However, in this work, with the high instrument resolution and data statistics we successfully observed a critical additional X shape band dispersing between 0.4 and 0.8 eV with the band crossing point (that is, Dirac point) at Eb∼0.5 eV at the
). However, in this work, with the high instrument resolution and data statistics we successfully observed a critical additional X shape band dispersing between 0.4 and 0.8 eV with the band crossing point (that is, Dirac point) at Eb∼0.5 eV at the  point—which is the long-sought-after TSSs, as we will discuss in details below.
point—which is the long-sought-after TSSs, as we will discuss in details below.
(a) FS maps of Bi-terminated LuPtBi (111) surface. Blue lines denote the surface BZ with high symmetry points labelled. The data has been symmetrized according to the crystal symmetry. (b,c) Zoom-in plot of FS map around the  point (b) and around the
point (b) and around the  and
and  points (c). (d,e) Plot of 3D electronic structure around the
points (c). (d,e) Plot of 3D electronic structure around the  point (d) and around the
point (d) and around the  and
and  points (e). All data were taken with 65 eV photons.
points (e). All data were taken with 65 eV photons.
Surface states on LuPtBi (111) surface
To help understand the origin of these electronic states, we carried out band structure calculations of Bi-terminated LuPtBi (111) surface with two different methods (Fig. 3a,b, see the ‘Methods’ section for more details), and both agree well with the measurement and clearly reproduce the X shape TSS observed in our measurements (Fig. 3c–f). In Fig. 3a, we first employed a slab model for the ab initio calculations (method one). This method, which takes into account the charge density redistribution due to surface potential modification by ab initio calculations, can describe all surface states including TSSs and those from the trivial dangling bonds. To further identify the TSS, we carried out another method (Fig. 3b) by calculating the k-resolved local density of states of a semi-infinite surface using the recursive Green's function (method two)34 constructed from Wannier function-based tight-binding parameters extracted from the bulk material35. Such method could reveal TSSs clearly and avoid the trivial surface states by removing the dangling bond orbitals in the Hamiltonian (as can be clearly seen in Fig. 3b).
(a,b) Calculated band structures of Bi-terminated LuPtBi (111) surface. (a) Result from a slab model calculation, in which the size of filled circles represent the projection to the Bi-terminated surface. Both topologically non-trivial surface state and metallic surface states are captured. (b) Results from a semi-infinite surface that is terminated by Bi. Only topologically non-trivial surface state is revealed by the calculation. (c,d) Photoemission intensity plot (c) and its second-derivative  plot (d) along the high symmetry
plot (d) along the high symmetry  –
– –
– directions. (e,f) Photoemission intensity plot (e) and its second-derivative
directions. (e,f) Photoemission intensity plot (e) and its second-derivative  plot (f) along the high symmetry
plot (f) along the high symmetry  –
– directions. SS, topologically trivial metallic surface state due to the dangling bonds on sample surface. TSS, topologically non-trivial surface state. All data were taken with 65 eV photons.
directions. SS, topologically trivial metallic surface state due to the dangling bonds on sample surface. TSS, topologically non-trivial surface state. All data were taken with 65 eV photons.
The combination of the two methods thus allows us to unambiguously identify the TSSs from other trivial dangling bond states (further experimental evidence of the non-trivial nature of the TSSs can be found in Supplementary Fig. 3 and Supplementary Note 2). As shown in Fig. 3a, all sharp dispersions (three Kramers pairs and one X shape state, labelled as SS1–SS3 and TSS respectively) are of surface origin and agree excellently with the observed band structures (Fig. 3c–f). Moreover, the three Kramers pairs (SS1, SS2 and SS3) are all absent in the result from method two (Fig. 3b) while the X shape band remains, illustrating their topologically trivial origin (that is, being trivial surface states due to dangling bonds), as opposite to the TSS shown in Fig. 3b.
The surface origin of both the TSS and SS1–SS3 in Fig. 3 can also be experimentally verified by performing the photon energy dependence photoemission measurement30, as presented in Fig. 4 (also in Supplementary Fig. 4 and Supplementary Note 3 along the other high symmetry direction). In Fig. 4a, dispersions along  –
– –
– directions measured using a wide range of photon energies (50–75 eV) were plotted, the dispersions of TSS and SS1–SS3 under all photon energies are identical (though the relative intensity can vary with photon energy due to the photoemission matrix element effect30). To further visualize the dispersion of these bands along kz, we extract the momentum distribution curves (MDCs) at EF (cutting through SS1 and SS2) and 0.65 eV below EF (cutting through TSS, SS2 and SS3) and plot them as the function of photon energy (see Fig. 4b,c). Evidently, the peaks from TSS and SS1–SS3 bands show no kz dispersion as they all form straight vertical lines. Thus, the surface nature of these bands (TSS and SS1–SS3) are clearly established. By fitting the Dirac type X shape linear dispersion (Fig. 4d), we can extract the band velocity at the Dirac point as 2.37 eV Å (3.59 × 105 m s−1) and 3.13 eV Å (4.74 × 105 m s−1) along the
directions measured using a wide range of photon energies (50–75 eV) were plotted, the dispersions of TSS and SS1–SS3 under all photon energies are identical (though the relative intensity can vary with photon energy due to the photoemission matrix element effect30). To further visualize the dispersion of these bands along kz, we extract the momentum distribution curves (MDCs) at EF (cutting through SS1 and SS2) and 0.65 eV below EF (cutting through TSS, SS2 and SS3) and plot them as the function of photon energy (see Fig. 4b,c). Evidently, the peaks from TSS and SS1–SS3 bands show no kz dispersion as they all form straight vertical lines. Thus, the surface nature of these bands (TSS and SS1–SS3) are clearly established. By fitting the Dirac type X shape linear dispersion (Fig. 4d), we can extract the band velocity at the Dirac point as 2.37 eV Å (3.59 × 105 m s−1) and 3.13 eV Å (4.74 × 105 m s−1) along the  –
– and
and  –
– direction, respectively.
direction, respectively.
(a) Photoemission intensity plots along the high symmetry  –
– –
– direction with photon energies from 50 to 75 eV. Two red dotted lines marked the energy where individual MDC is taken to generate the plots in b,c. (b,c) Intensity plot of the MDCs taken at EF (b) and EF—0.65 eV (c) at different photon energies. The MDC peak positions of all the observed bands are labelled (SS1–SS3 and TSS). (d) Zoom-in intensity plots of the TSS along the
direction with photon energies from 50 to 75 eV. Two red dotted lines marked the energy where individual MDC is taken to generate the plots in b,c. (b,c) Intensity plot of the MDCs taken at EF (b) and EF—0.65 eV (c) at different photon energies. The MDC peak positions of all the observed bands are labelled (SS1–SS3 and TSS). (d) Zoom-in intensity plots of the TSS along the  –
– direction and the
direction and the  –
– direction. Dirac points of the TSS are labelled. Data are taken with 60 eV photons. (e–g) Measured electronic structure of (111) surface of YPtBi. (e) The FS mapping of (111) surface of YPtBi with the hexagonal BZ (overlaid blue lines). The data has been symmetrized according to the crystal symmetry. (f,g) Photoemission intensity (f) and its second-derivative
direction. Dirac points of the TSS are labelled. Data are taken with 60 eV photons. (e–g) Measured electronic structure of (111) surface of YPtBi. (e) The FS mapping of (111) surface of YPtBi with the hexagonal BZ (overlaid blue lines). The data has been symmetrized according to the crystal symmetry. (f,g) Photoemission intensity (f) and its second-derivative  plot (g) along the high symmetry
plot (g) along the high symmetry  –
– –
– direction. Data in e–g are taken with 70 eV photons at T=20 K. SS, topologically trivial metallic surface state due to the dangling bonds on sample surface. TSS, topologically non-trivial surface state.
direction. Data in e–g are taken with 70 eV photons at T=20 K. SS, topologically trivial metallic surface state due to the dangling bonds on sample surface. TSS, topologically non-trivial surface state.
Surface states on YPtBi (111) and LnPtBi (001) surface
Similarly, for the other compound YPtBi, our calculation and measurements also agree well and both clearly show the TSS (Fig. 4e–g, also see Supplementary Fig. 5 and Supplementary Note 4 for the calculation). More measurements, as well as calculations on different cleaved surfaces (001) and different termination layers (Bi or Ln terminations), are presented in Supplementary Figs 6 and 7 and Supplementary Note 5, all showing excellent agreements. Interestingly, in both compounds, the observed TSS coexist and overlap in energy with the bulk valence band (appear as broad dispersing background intensity in Figs 3 and 4), demonstrating its unusual robustness.
Circular dichroism (CD)-ARPES of LuPtBi surface states
CD-ARPES measurement on the Bi-terminated (111) surface of LuPtBi has also been carried out (see Fig. 5). As one can see from the cut along the  –
– direction, the photoemission spectra intensity under circularly polarized right (CR) or circularly polarized left (CL) photons only emphasizes one of the two branches of SS3 and TSS bands, showing clear circular dichroism as reflected in the CR–CL difference spectrum (Fig. 5a and the peak analysis of the MDCs at various energies in Fig. 5c). The obvious dichroic photoemission results are in consistence with the non-degenerate spin configurations in SS3 and TSS, as indicated by the spin-resolved ab initio calculations (see Supplementary Fig. 8 in Supplementary Note 6). We note that due to the complexity of the asymmetry of measurement geometry and orbitals effect in CD-ARPES36, we encourage future spin-ARPES measurements for a more quantitative measurement on the spin polarization of TSS and SS3 bands.
direction, the photoemission spectra intensity under circularly polarized right (CR) or circularly polarized left (CL) photons only emphasizes one of the two branches of SS3 and TSS bands, showing clear circular dichroism as reflected in the CR–CL difference spectrum (Fig. 5a and the peak analysis of the MDCs at various energies in Fig. 5c). The obvious dichroic photoemission results are in consistence with the non-degenerate spin configurations in SS3 and TSS, as indicated by the spin-resolved ab initio calculations (see Supplementary Fig. 8 in Supplementary Note 6). We note that due to the complexity of the asymmetry of measurement geometry and orbitals effect in CD-ARPES36, we encourage future spin-ARPES measurements for a more quantitative measurement on the spin polarization of TSS and SS3 bands.
(a) Photoemission intensity around  along
along  –
– directions with the right and left circularly polarized (CR and CL) photons, showing clear asymmetry in the difference spectrum CR–CL. Dotted lines on the CR–CL spectrum represent the positions of the MDCs being analysed. Coloured marks label the position of the peaks fitted from the MDC curves in c. Red/Blue solid/dotted curves are the same as in b. (b) Red (Blue) solid curves give eye guides to the branch of bands which is enhanced with the CR (CL) photons, while blue (red) dotted curves give eye guides to the branch of bands which is suppressed with the CR (CL) photons. In the difference CR–CL spectrum both branches of SS3 and TSS could be seen. (c) MDCs analysis at the marked energy positions in a. Each fitted peak curve is drawn in colour, with the peak positions labelled with marks of same colour.
directions with the right and left circularly polarized (CR and CL) photons, showing clear asymmetry in the difference spectrum CR–CL. Dotted lines on the CR–CL spectrum represent the positions of the MDCs being analysed. Coloured marks label the position of the peaks fitted from the MDC curves in c. Red/Blue solid/dotted curves are the same as in b. (b) Red (Blue) solid curves give eye guides to the branch of bands which is enhanced with the CR (CL) photons, while blue (red) dotted curves give eye guides to the branch of bands which is suppressed with the CR (CL) photons. In the difference CR–CL spectrum both branches of SS3 and TSS could be seen. (c) MDCs analysis at the marked energy positions in a. Each fitted peak curve is drawn in colour, with the peak positions labelled with marks of same colour.
Discussion
Our discovery of the unusual TSSs on these materials establishing them as first examples with non-trivial topological electronic structure showing unusual robustness in Heusler materials with great tenability due to the vast number of compounds in the family. The non-trivial topology in the electronic structure can also help the understanding of various exotic properties recently discovered in half-Heusler compounds, including the large magnetoresistance29, chiral anomaly and Weyl fermions37,38 and their unconventional superconductivity39,40. Moreover, the interplay between topological electronic structure and the rich properties in Heusler materials further makes them ideal platforms for the realization of novel topological effects (for example, exotic particles including image monopoles41 and axions42) and new topological phases (for example, strain induced topological phase transition14 and topological superconductors).
Methods
Angle-resolved photoemission spectroscopy
ARPES measurements on single crystals LnPtBi (Ln=Lu, Y) were performed at beamline 10.0.1 of the Advanced Light Source (ALS) at Lawrence Berkeley National Laboratory, USA and beamline I05 of the Diamond Light Source (DLS), UK. The measurement pressure was kept below 3 × 10−11/8 × 10−11 Torr in ALS/DLS, and data were recorded by Scienta R4000 analysers at 20 K sample temperature at both facilities. The total convolved energy and angle resolutions were 16 meV/30 meV and 0.2°/0.2° at ALS/DLS, respectively. ARPES circular dichroism measurement was performed at BL5-4 of the Stanford Synchrotron Radiation Lightsource, SLAC national laboratory with 20 eV photons.
Ab initio calculations
To simulate a surface, a 54-atomic-layer thick slab model was used with a vacuum more than 10 Å to diminish the coupling between the top and bottom surfaces. The ab initio calculations were performed within the framework of the density functional theory and generalized gradient approximation43,44. In the bulk calculations, the density functional theory Bloch wave functions were projected to Wannier functions35, Ln-d, Pt-sd and Bi-p atomic like orbitals. In a half-infinite surface model, we projected the Green function of the bulk to the surface unit cell and obtained the surface local density of states based on the Wannier functions.
We could also calculate the surface bandstructure from tight binding model on the Bi-terminated (111) surface of LuPtBi. The metallic surface states (Fig. 4, SS1–SS3) observed on the Bi-terminated LuPtBi (111) surface all exhibit large spin splitting, thus reflecting very large SOC strength. The surface state SS1 constitutes the FS, in particular, around the  and
and  points (Fig. 2). They are mainly composed by Bi-pz orbitals of the top Bi layer. The surface Bi atoms form a triangular lattice.
points (Fig. 2). They are mainly composed by Bi-pz orbitals of the top Bi layer. The surface Bi atoms form a triangular lattice.
We wrote the effective tight-binding model for the SS1 surface states by considering the nearest neighbour hopping:




(1) About the nearest neighbour hopping. We consider a triangle lattice as illustrated in Supplementary Fig. 9. We take the lattice parameter a=1 and in-plane lattice vectors:  The six nearest sites of the site 0 are in unit of the lattice vectors: R1=−R4=(1, 0), R2=−R5=
The six nearest sites of the site 0 are in unit of the lattice vectors: R1=−R4=(1, 0), R2=−R5= and R3=−R6=
and R3=−R6= .
.
For a single pz orbital on the triangular lattice

where kx, ky are scaled by the unit of  .
.
(2) The Rashba term can be written as

where  ,
,  and
and  .
.
The Rashba Hamiltonian is

(3) The Kane–Mele term  . In the triangular lattice, the value of
. In the triangular lattice, the value of  depends on the hopping direction, as shown in Supplementary Fig. 9. We derived this term as
depends on the hopping direction, as shown in Supplementary Fig. 9. We derived this term as

We fitted the surface band structure using the parameters t=0.35, α=0.5 and β=0.1 and well reproduced the ab initio surface states (Supplementary Figs 9 and 10). Without the Kane–Mele term, the band degeneracy cannot be lifted at the  point, although
point, although  is not time-reversal invariant.
is not time-reversal invariant.
Recently a similar SOC effect45 has been employed to describe the surface states on the Tl/Si(111)–(1 × 1) surface46. Existence of strong Rashba effect and the unconventional SOC effect from the surface and the non-centrosymmetric bulk induces significant effect such as weak antilocalization and high mobility in transport measurements, and makes the LnPtBi a feasible candidate for spintronics applications.
Data availability
All relevant data are available on request, which should be addressed to Y.L.C.
Additional information
How to cite this article: Liu, Z. K. et al. Observation of unusual topological surface states in half-Heusler compounds LnPtBi (Ln=Lu, Y). Nat. Commun. 7, 12924 doi: 10.1038/ncomms12924 (2016).
References
Qi, X. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Ando, Y. Topological insulator materials. J. Phys. Soc. Jpn 82, 102001 (2013).
Yan, B. & Zhang, S.-C. Topological materials. Rep. Prog. Phys. 75, 096501 (2012).
Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nat. Commun. 3, 982 (2012).
Dziawa, P. et al. Topological crystalline insulator states in Pb1−xSnxSe. Nat. Mater. 11, 1023–1027 (2012).
Liu, Z. K. et al. Discovery of a three-dimensional topological dirac semimetal, Na3Bi. Science 343, 864–867 (2014).
Liu, Z. K. et al. A stable three-dimensional topological dirac semimetal Cd3As2 . Nat. Mater. 13, 677–681 (2014).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Yang, L. X. et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 11, 728–732 (2015).
Chadov, S. et al. Tunable multifunctional topological insulators in ternary Heusler compounds. Nat. Mater. 9, 541–545 (2010).
Lin, H. et al. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nat. Mater. 9, 546–549 (2010).
Ruan, J. et al. Symmetry-protected ideal Weyl semimetal in HgTe-class materials. Nat. Commun. 7, 11136 (2016).
Canfield, P. C. et al. Magnetism and heavy fermion-like behavior in the RBiPt series. J. Appl. Phys. 70, 5800 (1991).
Aoki, Y., Sato, H. R., Sugawara, H. & Sato, H. Anomalous magnetic properties of Heusler superconductor YbPd2Sn. Phys. C: Supercond. 333, 187–194 (2000).
Butch, N. P., Syers, P., Kirshenbaum, K., Hope, A. P. & Paglione, J. Superconductivity in the topological semimetal YPtBi. Phys. Rev. B 84, 220504 (2011).
Goll, G. et al. Thermodynamic and transport properties of the non-centrosymmetric superconductor LaBiPt. Phys. B: Condens. Matter 403, 1065–1067 (2008).
Tafti, F. F. et al. Superconductivity in the noncentrosymmetric half-Heusler compound LuPtBi: a candidate for topological superconductivity. Phys. Rev. B 87, 184504 (2013).
Fisk, Z. et al. Massive electron state in YbBiPt. Phys. Rev. Lett. 67, 3310 (1991).
Xu, G. et al. Weak antilocalization effect and noncentrosymmetric superconductivity in a topologically nontrivial semimetal LuPdBi. Sci. Rep. 4, 5709 (2014).
Pan, Y. et al. Superconductivity and magnetic order in the noncentrosymmetric half-Heusler compound ErPdBi. Europhys. Lett. 104, 27001 (2013).
Yan, B. & de Visser, A. Half-Heusler topological insulator. MRS Bull. 39, 859–866 (2014).
Feng, W., Wen, J., Zhou, J., Xiao, D. & Yao, Y. First-principles calculation of topological invariants within the FP-LAPW formalism. Comput. Phys. Commun. 183, 1849–1859 (2012).
Fu, L. & Berg, E. Odd-parity topological superconductors: theory and application to CuxBi2Se3 . Phys. Rev. Lett. 105, 097001 (2010).
Xiao, D. et al. Half-Heusler compounds as a new class of three-dimensional topological insulators. Phys. Rev. Lett. 105, 096404 (2010).
Liu, C. et al. Metallic surface electronic state in half-Heusler compounds RPtBi (R=Lu, Dy, Gd). Phys. Rev. B 83, 205133 (2011).
Chandra, S. et al. Large linear magnetoresistance and weak anti-localization in Y(Lu)PtBi topological insulators. Preprint at http://arxiv.org/abs/arXiv:1502.00604 (2015).
Hou, Z. et al. Extremely high electron mobility and large magnetoresistance in the half-Heusler semimetal LuPtBi. Phys. Rev. B 92, 235134 (2015).
Chen, Y. L. Studies on the electronic structures of three-dimensional topological insulators by angle resolved photoemission spectroscopy. Front. Phys. 7, 175–192 (2012).
Chu, R.-L., Shan, W.-Y., Lu, J. & Shen, S.-Q. Surface and edge states in topological semimetals. Phys. Rev. B 83, 075110 (2011).
Wu, S.-C., Yan, B. H. & Felser, C. Ab initio study of topological surface states of strained HgTe. Europhys. Lett. 107, 57006 (2014).
Brüne, C. et al. Quantum Hall effect from the topological surface states of strained bulk HgTe. Phys. Rev. Lett. 106, 126803 (2011).
Sancho, M. P. L., Sancho, J. M. L. & Rubio, J. Quick iterative scheme for the calculation of transfer matrices: application to Mo (100). J. Phys. F: Metal Phys. 14, 1205 (1984).
Mostofi, A. A. et al. wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Schönhense, G., Westphal, C., Bansmann, J. & Getzlaff, M. Circular dichroism in photoemission from nonmagnetic, low-Z solids: a conspicuous effect of the photon spin. Europhys. Lett. 17, 727 (1992).
Hirschberger, M. et al. The chiral anomaly and thermopower of Weyl fermions in the half-Heusler GdPtBi. Preprint at http://arxiv.org/abs/arXiv:1602.07219 (2016).
Shekhar, C. et al. Observation of chiral magneto-transport in RPtBi topological Heusler compounds. Preprint at http://arxiv.org/abs/arXiv:1604.01641v1 (2016).
Kim, H. et al. Beyond spin-triplet: nodal topological superconductivity in a noncentrosymmetric semimetal. Preprint at http://arxiv.org/abs/arXiv:1603.03375v2 (2016).
Nakajima, Y. et al. Topological RPdBi half-Heusler semimetals: a new family of noncentrosymmetric magnetic superconductors. Sci. Adv. 1, 5 (2015).
Qi, X.-L., Li, R., Zang, J. & Zhang, S.-C. Inducing a magnetic monopole with topological surface states. Science 323, 1184–1187 (2009).
Li, R., Wang, J., Qi, X.-L. & Zhang, S.-C. Dynamical axion field in topological magnetic insulators. Nat. Phys. 6, 284–288 (2010).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Nakajin, K. & Murakami, S. Theory of unconventional spin states in surfaces with non-Rashba spin–orbit interaction. Phys. Rev. B 91, 245428 (2015).
Sakamoto, K. et al. Abrupt rotation of the Rashba spin to the direction perpendicular to the surface. Phys. Rev. Lett. 102, 096805 (2009).
Acknowledgements
Y.L.C. acknowledges the support of the EPSRC Platform Grant (Grant No. EP/M020517/1) and Hefei Science Center CAS (2015HSC-UE013). C.F. acknowledges the financial support by the ERC Advanced Grant (No. 291472 ‘Idea Heusler’). J.J. acknowledges the support of the NRF, Korea through the SRC Center for Topological Matter (No. 2011-0030787). The ALS is supported by the Office of Basic Energy Sciences of the U.S. DOE under Contract No. DE-AC02-05CH11231. H.F.Y. acknowledges the finacial support from the Bureau of Frontier Sciences and Education, Chinese Academy of Sciences.
Author information
Authors and Affiliations
Contributions
Y.L.C. conceived the experiments. Z.K.L. and L.X.Y. carried out ARPES measurements with the assistance of J.J., H.F.Y., Y.Z. and S.-K.M. C.S. synthesized and characterized the bulk single crystals. S.-C.W. and B.Y. performed ab initio calculations. All authors contributed to the scientific planning and discussions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-10 and Supplementary Notes 1-6 (PDF 1617 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Liu, Z., Yang, L., Wu, SC. et al. Observation of unusual topological surface states in half-Heusler compounds LnPtBi (Ln=Lu, Y). Nat Commun 7, 12924 (2016). https://doi.org/10.1038/ncomms12924
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12924
This article is cited by
-
Stability and Thermoelectric Properties of FeZrTe Alloy
Journal of Electronic Materials (2023)
-
Efficient spin current source using a half-Heusler alloy topological semimetal with back end of line compatibility
Scientific Reports (2022)
-
First-principles calculations for topological quantum materials
Nature Reviews Physics (2021)
-
Epitaxy, exfoliation, and strain-induced magnetism in rippled Heusler membranes
Nature Communications (2021)
-
Strain driven emergence of topological non-triviality in YPdBi thin films
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.