Main

The investigation has become possible through two recent findings concerning atomic ionization dynamics in strong laser fields. First, neutral atoms can survive a strong laser field in a (long-lived) excited state13, in which they can be detected directly in an atomic beam by means of a standard electron or ion detector14. Thus, any momentum transferred to the neutral atom can easily be detected. Second, according to the physical picture behind the excitation process, the excited electron behaves as a quasi-free electron during the laser pulse. More precisely, the excitation process can be viewed as a frustrated tunnel ionization14 within the three-step model for strong-field ionization15.

In the first step, the electron tunnels in the close vicinity of the maximum electric field of a laser cycle. The liberated electron is then driven by the laser field with an amplitude that slowly decreases with decreasing pulse intensity; in this way an active damping of the electronic motion takes place. After the laser pulse the electron is left with a drift energy too low to overcome the Coulomb potential of the ion and is recaptured into a Rydberg state. The quivering quasi-free electron experiences the ponderomotive force during the laser pulse owing to the intensity gradient in the focused laser beam. We will show here that the quiver motion of the electron is partially converted into centre-of-mass motion of the neutral atom, leading to a substantial acceleration. This results in a measurable momentum transfer to the atom despite the short interaction time in the femtosecond range. Remarkably, the ponderomotive effect is typically estimated to be negligible for these conditions16,17 with, however, a few exceptions18. We note that the investigation relies on the highly selective process of excitation of neutrals in a strong laser field, where kinematic effects are imparted only through the gradient of the laser field.

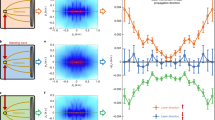
In the experiment we excite neutral He atoms in an effusive atomic beam using a perpendicularly intersecting focused laser beam. Using the detection technique (see the Methods) we measure the distribution of excited He atoms on a detector as shown in Fig. 1. If, during the laser pulse, no momentum is transferred to the atoms, we would expect a slightly enlarged projected image of the (laser-intensity-dependent) distribution of excited atoms in the laser beam on the detector, that is, a distribution that extends along the laser beam direction (z axis), typically within the Rayleigh length, but with a very narrow radial distribution (rD axis) of the order of the size of the laser beam waist.

Figure 1: Deflection of neutral He atoms after interaction with a focused laser beam.
figure 1

a, Distribution of excited He* atoms on the detector (colour scale, in number of atoms). The laser beam direction is indicated by the arrow. b, Cut through the atom distribution along the laser beam axis (z axis) at rD = 0 mm (black curve) and full projection on z axis (dashed red curve) and intensity along the z axis in units of the laser peak intensity I0 = 6.9 × 1015 W cm–2 (blue curve). c, Cuts through the distribution at z = 0 mm (red curve) and z = -2.7 mm (black curve). The black curve shows the velocity distribution of excited neutral atoms at a position unaffected by the ponderomotive force, showing essentially the ‘natural’ velocity spread, while the red curve shows the velocity gain through the ponderomotive force.

PowerPoint slide

Full size image

In Fig. 1a, however, we see a strikingly large radial distribution of excited atoms with a strong maximum in the laser focal plane (z = 0) that obviously stems from a deflecting radial force during the laser pulse. In Fig. 1b the cut along the z axis (black curve) shows two maxima at roughly half the laser peak intensity I0/2, where the net production rate of excited helium atoms He* is apparently maximum, whereas the He* signal at I0 shows a pronounced minimum. However, the loss of neutral excited atoms is largely due to their radial deflection. The full projection (red dashed curve) shows only a slight decrease in signal, indicating that even at the highest intensities He atoms are excited. The data are taken at a low beam target pressure of  mbar. The radial deflection is unchanged when we increase the target pressure by more than a factor of 30. This excludes many-particle effects based on atom density or space charge as an origin of our observations. Furthermore, we emphasize that the radial distribution is unaltered whether the linear polarization of the laser beam is in the direction of the atomic beam or perpendicular to it. In this respect the intensity-dependent force very much resembles the ponderomotive force acting on charged particles. The question arises whether we can conclude that the ponderomotive force is responsible for the observed centre-of-mass motion of the neutral particle.

To shed light on the underlying process we first recall that the ponderomotive force Fp on a charged particle is given by (all equations are in atomic units):

Here, m and q are the mass and the charge of the particle, respectively, E(r, t) = E0(r, t)expiωt is the electric field, ω is the field frequency and E0(r, t) is the slowly varying field amplitude. Hence, in view of our frustrated tunnel ionization model, both the ionic core and the electron experience a mass-dependent ponderomotive force during the laser pulse. As a consequence of the mass dependency, however, the ionic core remains practically unaffected while the electron experiences a non-negligible ponderomotive force. This, in turn, means that to the first approximation a ponderomotive force acts directly on the centre-of-mass motion of the atom and leaves the recapturing process unaffected. This can be shown more rigorously: we derive the centre-of-mass motion from the Lorentz force (see the online-only Methods). Recalling the key point of our investigation, that the electron remains bound after interaction with the laser pulse, we are able to observe the centre-of-mass motion. Furthermore, by solving the coupled Lorentz equations for the electron and the ion, including the Coulomb potential, we can directly reproduce the capture process into bound Rydberg orbits and the force on the centre of mass.

According to our model we can rewrite equation (1) for the centre-of-mass position R of the neutral atom:

Here, M and me ( = 1 atomic unit) are the masses of the atom and the electron, respectively, and is the second derivative of the centre-of-mass position R with respect to time. To calculate the ponderomotive force explicitly, we assume a linearly polarized laser beam with a Gaussian spatial intensity distribution, which reads, in cylindrical coordinates:

where , w0 is the beam waist. Evaluating the gradient in equation (2) with the intensity distribution given by equation (3), we obtain, for the radial component of the centre-of-mass position perpendicular to the laser beam direction:

where f(t) is the laser pulse envelope, which we assume to be of the form f(t) = exp(–t2/τ2), where τ is the pulse width. From equation (4) we find that the maximum force along the radial direction scales as . Similarly, one can show that it scales as along the laser beam direction. Because the Rayleigh length z0 is typically a factor of 100 larger than the beam waist r0, the gradient and thus the ponderomotive force in the laser beam direction is much smaller than in the radial direction and can be neglected. (However, the situation would be very different if we used a short-pulse standing-wave laser field. We would then obtain a strong periodic intensity gradient on the scale of the laser wavelength, and might expect to see the Kapitza–Dirac effect for neutral atoms in an intense standing-wave laser field instead of electrons19).

To solve equation (4), we assume that the neutral atom does not move significantly during the laser pulse. Hence, we set r(t) = r on the right-hand side of the equation, which allows us to solve equation (4) analytically for any initial position of an atom in the laser beam. We will concentrate our analysis on atoms located at the half beam size r0/2, which experience the maximum force. Solving equation (4) for these conditions by integrating over the full laser pulse, we find the maximum velocity vmax(z):

If we evaluate equation (5) at the focal plane for He atoms exposed to our focused laser beam at maximum intensity, we obtain a velocity of about 55 m s-1 from which accelerations of about 2 × 1014g can be deduced.

This exceeds the typical acceleration (deceleration) of neutral atoms20 or molecules in external fields21,22. Compared to laser-cooling experiments in a continuous-wave laser field, for instance, which are based on photon momentum transfer with a typical deceleration of about 106g (ref. 20), the acceleration present in our experiment is eight orders of magnitude larger. It is, to the best of our knowledge, by far the largest acceleration of neutral matter by electromagnetic fields ever observed.

Finally, we mention that a different but equivalent description of our process might be given in terms of an atom in the Kramers–Henneberger reference frame23, which is expected to exhibit stable configurations in a strong electromagnetic field. Our observations of accelerated neutral atoms seem to be a direct confirmation of the existence of this exotic type of stable atom.

In Fig. 2 we show the results of a systematic investigation of He atoms exposed to laser light of different laser pulse lengths and laser pulse energy EL, such that the laser intensity is kept constant. We obtain neutral excited atom distributions similar to the one shown in Fig. 1. The maximum radial deflection of the atoms along the laser beam axis, which can be converted into maximum velocity vmax(z), can reliably be extracted from the experimental data to compare with equation (5). Fitting equation (5) to the data gives very good agreement, confirming the validity of our model. The fit contains only three free parameters: a small velocity offset, a common constant beam waist w0, and a scaling factor for the absolute velocity. The best choice of the latter implies that the acceleration must last over the whole pulse duration, confirming the assumption that the electrons are set free early during the laser pulse.

Figure 2: Maximum velocity vmax(z ) gained by neutral He atoms.
figure 2

a–e, vmax(z) extracted from measurements at constant laser peak intensity I0 = 2.8 × 1015 W cm–2 (3.4 × 1015 W cm–2), but for different pulse energies EL and pulse durations τFWHM: a, 600 µJ, 40 fs; b, 900 µJ, 60 fs; c, 1.2 mJ, 80 fs; d, 1.5 mJ, 100 fs; e, 1.8 mJ, 120 fs. FWHM, full-width at half-maximum. The red curves are fits to the data based on equation (5). The fitted common beam waist w0 = 16.0 µm is in good agreement with an independent experimental determination of w0 = 17.5 ± 1.5 µm using the knife-edge method. It results, however, in a higher laser peak intensity, which is indicated in parentheses. f, vmax(z) for laser parameters EL = 1.8 mJ and τFWHM = 40 fs corresponding to I0 = 8.3 × 1015 W cm–2 (10 × 1015 W cm–2). The error bars are estimated from the accuracy of the maximum deflection we determined.

PowerPoint slide

Full size image

Even then the observed velocities lie slightly above the theoretical prediction (see Fig. 3), which we attribute to absolute laser intensity uncertainties or a slightly non-Gaussian intensity distribution. Hence, we note that the radial velocity vmax(z) might serve as a valuable beam shape and intensity parameter along the laser beam axis. On the one hand it measures the peak intensity if the radial intensity distribution is known (for example, Gaussian), or, on the other hand, indicates systematic deviations from the Gaussian beam shape if the peak intensity is known (for example, from ionization experiments). Such information is otherwise rather difficult to obtain.

Figure 3: Maximum velocity v max (0) transferred to He and Ne at the focal plane as a function of the laser pulse duration at constant laser intensity.
figure 3

vmax(0) is plotted for He (black squares) and Ne (red circles) measured at I0 = 2.8 × 1015 W cm–2 (3.4 × 1015 W cm–2); see explanation in Fig. 2. The dashed black and red curves show the calculated velocities, respectively, using equation (5) with the fitted beam waist, but omitting the scaling factor. The full curves are fits to the data. The error bars are determined as in Fig. 2.

PowerPoint slide

Full size image

We have also measured the radial deflection of a beam of Ne atoms, which is, however, smaller than in He, as expected owing to the larger mass. In Fig. 3 we show the maximum velocity vmax(z = 0) transferred to Ne atoms exposed to a laser beam kept at a constant laser intensity of I0 = 2.8 × 1015 W cm–2, but at different pulse durations and energies. For comparison, the maximum velocities for He are also shown. The data clearly show the excellent quantitative agreement of the observed deflection with our theoretical predictions. Within the range of our achievable pulse durations the deflection is proportional to the mass and the time the force is acting on the atom.

In conclusion, we have demonstrated ultrastrong acceleration of neutral atoms, using femtosecond laser pulses with intensities of up to I0 = 1016 W cm–2. We present a quantitative theoretical model based on the concept that a bound electron temporarily undergoes a quasi-free oscillatory quiver motion during the laser pulse while still being coupled to the ion by the Coulomb force. The inhomogeneous field of a focused laser beam causes a ponderomotive force on the electron, resulting in a centre-of-mass acceleration of the whole atom. Many new applications may be envisioned, considering that the mechanism transfers the momenta of a large number (presently of the order of 103) of photons quasi-instantaneously onto neutral atoms, without any problems due to Doppler detuning, as in the case of resonant continuous-wave laser absorption. Atom optics, controlled atom deposition or controlled chemical reactions are just some of them. The acceleration process may be considerably refined by sophisticated spectral and temporal shaping of the accelerating laser beam, including the use of standing (or slowly moving) waves with much steeper field gradients, or the use of longer pulse durations for achieving substantially larger atomic momenta.

Methods Summary

The observation of acceleration of neutral atoms in strong laser fields is based on the method of producing and detecting excited neutral atoms in strong laser fields introduced in ref. 14. In the online-only Methods we give a detailed description of how to adapt the method to the present experiments. Furthermore, we detail the theoretical background of the underlying process and derive the respective formulas used to describe our data.

Online Methods

Experimental set-up and detection of excited neutral atoms

We use a slightly modified version of an experimental set-up that has been described elsewhere14. Briefly, a linearly polarized Ti:sapphire laser beam with a repetition rate of 500–1,000 Hz, a variable pulse width of τFWHM = 40–120 fs and pulse energies up to 2.5 mJ is steered into a vacuum chamber with a base pressure of ∼10-9 mbar. It is focused by means of a plano-convex lens with a focal length of 0.2 m into an effusive beam of He or Ne atoms at right angles, where, among other processes, it excites neutral atoms. The beam target pressure is typically ≤5 × 10-7 mbar. 0.38 m downstream in the direction of the atomic beam, a position-sensitive microchannel plate detector is located. The detector can be configured to detect either ions or electrons in the counting mode. Both configurations are suitable for excited neutral species detection, if they have an excitation energy of more than ∼5 eV. In contrast to charged particles, which are easily accelerated by small electric fields (either deliberately applied or stemming from spurious charges) and hit the detector after a few microseconds, neutral atoms travel at thermal velocities reaching the detector only after hundreds of microseconds. Consequently, the excited state needs to survive long enough that the atom can reach the detector in an excited state. It has been found in earlier work14 that an intense laser interacting with a beam of rare gas atoms produces mainly Rydberg states with principal quantum numbers around n = 10, which decay partially to a metastable state with high excitation energy, for example, ∼20 eV in He. The metastable state lives long enough to reach the detector. We estimate that about 1% of all excited atoms reach the detector in an excited state.

Owing to the divergence of the atomic beam, the signal on the detector in laser beam direction is an image enlarged by a factor of 2.3 of the distribution of excited atoms in the laser beam, in case the momentum transferred to the atom during the excitation can be neglected. This needs to be taken into account when transforming the detector signal along the zD coordinate into the laser beam z coordinate. The high detection sensitivity to accelerating forces during the laser pulse lies in the nature of neutral excited atoms travelling with thermal velocities. The time-of-flight distribution of He atoms at the microchannel plate detector peaks around 230 µs. Because momentum is only transferred to the atoms during the laser pulse duration, the starting point of the atoms is well defined. By setting a 40-µs-wide gate on the maximum of the time-of-flight distribution, a precise determination of the radial velocity can be calculated from the radial beam deflection on the detector. We note that the centre-of-mass motion of a neutral atom is largely unaffected by spurious electric fields or space charge.

Derivation of the ponderomotive centre-of-mass force on neutral atoms

To derive the centre-of-mass force on the neutral atom we solve the coupled Lorentz equations for the ion with mass m1 and charge q1 and electron with mass m2 and charge q2 including the Coulomb interaction between them. The two Lorentz equations in atomic units read:

where and . The Coulomb force Fc is given by . Using the first-order electric and magnetic fields for a focused Gaussian beam24, we can write the equations explicitly:

Equation (2) can be derived analytically from the Lorentz forces using centre-of-mass and relative coordinates. We obtain the force on the centre-of-mass by using the following approximations. The fields are approximated to first order and we assume the slowly varying amplitude approximation; the relative velocity and position are approximated through the motion of the electron in the electric field in polarization (x) direction, neglecting the Coulomb force.

By solving equations (8) and (9) numerically without the aforementioned approximations, we obtain, for specific initial conditions, the bound trajectories of the tunnel electron at the end of the laser pulse as described in ref. 14. Most importantly, by evaluating the centre-of-mass velocity from the numerical calculations we confirm the results of equation (2).

To give an interpretation of why the electron remains bound, we first note that its motion during the laser pulse is mainly driven by the laser field. If we suppose that the electron starts at a maximum of a field cycle close to the nucleus, that is, where the Coulomb field is strong, the electron then revisits its starting (inner turning) point periodically with the laser frequency. Here, the attractive force is strongly peaked. For example, if the electron is set free at a distance of 10 atomic units (a.u.) from the nucleus, the Coulomb force is 10-2 a.u. acting for roughly a tenth of the laser cycle duration. If one compares this periodical force with the steady ponderomotive force Fp, which is of the order of 10-4 a.u. for I = 0.1 a.u. and beam waist of w0 = 16 µm we find an attractive net force.

Sign of the centre-of-mass force on a neutral atom in a laser field

A focus of a continuous-wave laser beam can act as a quasi-static dipole trap for neutral atoms12 provided the photon energy of the laser is much below the lowest excited state. In this case the atom is a strong-field seeker. In our experiment, the force on the centre-of-mass motion according to equation (4) is outward bound, that is, the atom in the strong short-pulsed laser field is a low-field seeker, although the photon energy of the laser field is much below the lowest excited state. Obviously, the effective polarizability of an atom in a strong laser field, where the electron can be treated as quasi-free, differs in sign from a ground-state atom in a weak continuous laser field, where the strongly bound electron is only weakly perturbed by the laser field. According to the analysis of ref. 25 there is a relationship between the dynamical polarizability of an atom and the ponderomotive potential for a free electron Up, from which the ponderomotive force can be obtained by Fp = –∇Up. For a quasi-free electron, as is the case for our experiments, . The more general ponderomotive potential for a bound electron with a binding frequency ωb is given by , which can be derived from the Lorentz model of atomic polarizability. It is immediately obvious that for a strongly bound electron with ω ≪ ωb the sign of the ponderomotive potential is opposite and the absolute value is much smaller than for a free electron.