Introduction

The association mapping has become a powerful tool for detecting quantitative trait loci (QTL) in plant and animal genomes. Standard regression-based methods assume that the quantitative traits are normally distributed. In reality, the sample may contain some outlying phenotypic observations (Estaghvirou et al., 2014). Besides, the data might be collected from different environments or populations, which result in quantitative trait following some skewed distributions (for example, with heavier tails than the normal distributions). Directly applying a normal distribution-based QTL/association mapping method on such skewedly distributed data or data with outliers may cause biased estimation of QTL effects and QTL locations (for example, reducing the statistical power to detect true QTLs).

One possible solution for handling non-normality is to perform some transformation to increase the normality in the phenotype data (Goh and Yap, 2009). Examples are logarithm, Box-Cox, arcsine (for proportion data) and rank-based transformations. However, it is generally unclear which transformation method is most appropriate for a particular data set. Alternatively, some statistical approaches have been proposed, which specify the residual errors in their models to follow some skewed distribution such as skew-normal distribution, Student’s t-distribution or Laplace distribution instead of normal distribution (Fernandes et al., 2007; Wang et al., 2009). Intuitively, such a regression model should be more robust to the non-normally distributed phenotype data and outliers. In this article, we focus on the Laplace residual errors corresponding to the least absolute deviations (LAD) method (Li et al., 2010), which is regarded as a robust alternative to the classical least squares estimation.

In association studies, multiple-locus methods refer to a class of regression methods that attempts to simultaneously estimate the additive effects of many markers in a single model. As a large number of markers (for example, single-nucleotide polymorphisms (SNPs)) are present in many association mapping data sets, the multiple-locus methods usually involve some variable selection or parameter regularization procedures to reduce the dimensionality of the model. Least absolute shrinkage and selection operator or the LASSO (Tibshirani, 1996) is a popular regularization method, and has been widely used for analyzing high-dimensional data in various applied fields including genetics (Li and Sillanpää, 2012). It is possible to combine the LASSO regularization with the LAD method to produce sparse estimation of genetic effects, which is also resistant to the outliers or non-normality in the phenotype data. In this work, we further generalize the idea of LASSO and LAD to identify the association between markers and multiple correlated quantitative traits or a single trait measured at multiple time points (that is, longitudinal data). Our approach is developed on the basis of Möttönen and Sillanpää (2015). In their work, they focused on variable selection and coefficient estimation of the QTL effects; whereas in our work, we incorporated multiple hypothesis testing to formally judge QTLs, and evaluated the methods on more biologically meaningful examples. Compared with the single-trait method, the multiple-trait analysis with proper modeling of grouping and covariance structure in the data may have the benefit to investigate the pleiotropy—the same gene influencing multiple traits which are (genetically) correlated.

The structure of this article is as follows. Materials and methods describe the robust multivariate LAD-LASSO model, its computational algorithm and the relevant QTL decision rules. In Results, our method was illustrated with a QTLMAS2009 simulated data set (Coster et al., 2010) and a real sugar beet data set (Würschum et al., 2011). We focus on the comparison between our robust multivariate LAD-LASSO and the multivariate normal LASSO method. Finally, we discuss the strengths and weaknesses of our LAD approach, and point out the future research directions.

Materials and methods

LAD-LASSO for single-trait analysis

A normal multiple linear regression for single-trait association mapping is defined by

where yi is the phenotype value of individual i (i=1,…,n), xi= [1, xi1,…,xip]T, xij is the genotype value of individual i and marker j (j=1,…..,p) coded as −1, 0 and 1 for three SNP genotypes AA, AB and BB, respectively, β=[β0,β1,…,βp]T, β0 is an intercept term, βj is the effect of marker j, and ɛi is the residual error, which is assumed to follow mutually independent normal distribution with zero mean and unknown variance .

According to normal residual errors in equation (1), the classical ordinal least squares (OLS) seek the minimization of an l2 objective function: the sum of squared error function The OLS estimates might not be optimal for the non-normally distributed phenotype data. A robust alternative is the LAD estimates, which minimize the sum of absolute error or l1 objective function The LAD estimates are in line with assuming the residual errors ɛi of model (1) to follow an i.i.d. Laplace distribution (Li et al., 2010):

A multiple-locus method for association mapping aims at estimating and testing for the effects of a huge number of SNPs simultaneously. In such a case, standard OLS or LAD methods often fail to provide such accurate estimates due to the limited sample size in the data. An improved estimation can be obtained by using regularization—adding a certain penalty function of SNP effects βj to the sum of squared error or sum of absolute error function. We consider the LASSO, or the l1 norm regularized method, defined for the sum of squared error case:

and for the sum of absolute error case:

We name (2) and (3) as normal LASSO and LAD-LASSO, respectively. In both (2) and (3), the inclusion of l1 norm penalty produces a sparse solution by shrinking the effects of many unimportant markers to zero. Note that no penalty is added to the intercept term β0. The tuning parameter λ(⩾0) determines the amount of shrinkage and degree of sparsity, an optimal value of which can typically be chosen by some model selection criteria such as cross validation (Hastie et al., 2009).

The normal LASSO estimates of (2) can be obtained by algorithms such as LARS (Efron et al., 2004) and coordinate descent method (Friedman et al., 2010). In LAD-LASSO (3), as both the sum of absolute error function and penalty term is in l1 norm, it is possible to combine these two components into one. Let , if i=1,...,n, and , if i=n+1,...,n+p, where ei is a 1 × p standard unit vector with the ith element to be 1, and others to be 0. Now the LAD-LASSO problem (3) can be re-defined as

Obviously, equation (4) becomes a standard LAD problem, which implies that any estimation algorithm developed for LAD or quantile regression (for example, Koenker and d’Orey, 1987; 1994) can be directly used for computing LAD-LASSO solutions.

Group LAD-LASSO for multiple-trait analysis

Now we turn to the multivariate regression for mapping multiple correlated traits, defined by

where yi=[yi1,…,yim]T is an m × 1 observation vector of the ith individual on traits k=1,…,m, xi is a vector of genotype data, which is defined in the same way as in equation (1), B is a (p+1) × m matrix consisting of effect for the jth SNP on mth trait, and ɛi is a vector of residual errors, following a multivariate normal distribution with zero mean vector and covariance matrix . Like in the univariate regression (1), the OLS estimates for (5) minimize an l2 objective function: where with locus effects of each trait B.k=(B0k, B1k, …, Bpk)T. In fact, the least squares estimates of the multivariate regression are given by assuming the covariance matrix to be an identity matrix, which is equivalent to the separate OLS estimates of each single trait, so that the possible covariance structure among multiple traits is not considered in the estimation stage. However, the covariance structure might be taken into account in the later hypothesis testing stage (Knott and Haley, 2000).

On the other hand, the robust LAD estimates for the multivariate regression minimize an l1 objective function:

The multivariate LAD corresponds to a multivariate Laplace residual error assumption: , with the scale matrix (which is proportional to the covariance matrix) to be an identity matrix just like in the least squares case. According to Gómez et al., (1998), the density function of the multivariate Laplace distribution is defined by where

In addition, the l1 and l2 multivariate regressions are extended to the following penalized regression forms:

and

respectively.

Here, is a group LASSO penalty (Yuan and Lin, 2006). Such a penalty is added to the effect parameters of each loci, but not to the intercept B0. By using the group LASSO penalty, selecting a marker is equivalent as selecting a vector of marker’s effects on each trait instead of selecting a single parameter, which differs from standard LASSO penalty in equations (2) and (3). Thus, the group LASSO penalty takes the dependencies among multiple traits explained by genetic effects into account, although in the original l1 and l2 objective functions, the multiple traits are in fact assumed to be independent from each other. We name equations (6) and (7) as multivariate group LASSO and multivariate group LAD-LASSO, respectively (abbreviated as MG-LASSO and MGLAD-LASSO).

Like in the univariate case, it is possible to combine the two components of MGLAD-LASSO into one. Let if i=1,…,n, and , if i=n+1,...,n+p. Equation (7) can now be rewritten as

which is a standard multivariate LAD problem. To solve equation (8), we used a fixed point algorithm introduced in Oja (2010), which is implemented by the R-package ‘MNM’ (Nordhausen and Oja, 2011). More details are explained in Appendix A.

The solution of MG-LASSO can be computed by a coordinate descent algorithm, implemented in the R-package ‘glmnet’ (Friedman et al., 2010; http://cran.rproject.org/web/packages/glmnet/glmnet.pdf).

QTL decision rules

By using the l1 penalized regression, the effects of unimportant markers are shrunk towards zero, and only the relatively important markers are left in the model. However, in practice, it is very difficult to choose an ‘optimal’ tuning parameter λ leading to the selection of a true set of QTLs. Use of standard criteria such as cross validation for determining λ may result in a large number of false-positive signals (Li and Sillanpää, 2012). Therefore, some QTL decision rules are needed to further filter out the false-positive markers. For both MG-LASSO and MGLAD-LASSO, we considered two decision-making procedures, including a stability selection method (Meinshausen and Bühlmann, 2010) and a multiple-split test method (Meinshausen et al., 2009) to formally judge the QTLs.

In stability selection, a subsample of the data is randomly chosen including half the number of individuals. The LASSO analysis is performed on this subsample of the data, and the set of markers with non-zero effects are being recorded. This procedure is repeated for many times (say 100 times). Then the stability selection probability of each marker being selected is calculated, and used to judge the support for QTLs. Meinshausen and Bühlmann (2010) suggested a decision rule on the basis of stability selection probabilities to control the expected number of false positives.

In multiple-split test, the data are randomly divided into two parts, preferably with equivalent sample size. The MGLAD-LASSO/MG-LASSO is implemented on the first part of the data to choose a subset of markers. In the second half of the data, the standard normal multivariate LAD regression (or least squares) without penalty are used on those selected markers, hypothesis testing is performed using unpenalized effect estimates, and the corresponding P-values for each selected marker are calculated. Such a procedure is repeated many times, and the P-values for each marker from multiple runs are combined into one and used for judging QTLs. The multiple-split test can control family-wise error, which should be more conservative than a method controlling false discovery rate such as the stability selection. We have earlier used the stability selection and the multiple-split test in the univariate case for the normal LASSO in Li et al. (2014).

More details about stability selection and multiple-split test method are shown in Appendix B and Appendix C, respectively. Some R codes for implementing these methods are provided as Supplementary Information.

Results

We consider (i) a simulated longitudinal QTLMAS2009 data set (Coster et al., 2010) and (ii) a real sugar beet data set (Würschum et al., 2011; Würschum and Kraft, 2013) for evaluating our proposed LAD-LASSO methods. The two data sets are available from their original publications: Coster et al. (2010) and Würschum and Kraft (2013), respectively.

Analysis and results: QTLMAS simulated data

The simulated data set includes 453 SNP markers distributed over five chromosomes of 1M each from 2025 individuals with a certain population structure and the growth traits following logistic curves y(t)=φ1/{1+exp[(φ2−t)/φ3]} measured over five time points (0, 132, 265, 397 and 530 days). Measurements at each single time point can be thought as a separate ‘quantitative trait’, and therefore a multiple-trait method can be used for analyzing such a longitudinal data set. In total, 18 additive QTLs were simulated, with six contributing to each of the three parameters φ1 (asymptotic yield), φ2 (inflection point) and φ3 (slope of the curve) of a growth curve. Besides, some i.i.d. Gaussian errors were also simulated to these three trait parameters. A subsample of 1000 individuals is used in our simulation analyses. The same subsample of individuals was also analyzed in Heuven and Janss (2010) and Li and Sillanpää (2013) by other approaches. In addition, for a group of markers with pairwise correlation coefficients higher than 0.9, only one marker was picked up to represent the whole group of the highly correlated markers to reduce the collinearity of the genotype data, and, therefore, there are only 393 markers used in the LASSO analysis.

Scenario 1: original QTLMAS data

Here, the MGLAD-LASSO and MG-LASSO methods were applied on the original simulated QTLMAS2009 data set. Note that neither MGLAD-LASSO nor MG-LASSO takes the serial correlation simulated in the QTLMAS2009 data set into account, and may not be optimal for analyzing such a longitudinal data set. In contrast, a varying coefficient method might be more appropriate for modeling the longitudinal data (Li and Sillanpää, 2013). Nevertheless, this data set can still be used to compare the performances of the two group LASSO methods. Both the methods were used together with the stability selection and multiple-split test to judge QTLs. In stability selection, we judge a marker as a putative QTL, if its stability selection probability is larger than a threshold, to guarantee the average number of false selected markers to be no greater than 1 (see Appendix B for more details). In multiple-split test, a marker is declared as significant if its P-value is <0.05. We claim that a true simulated QTL is successfully identified if a significant marker is located within 10 cM of this simulated QTL, and otherwise the marker was judged as a false positive. Note that the same QTL identification rule will also be used in Scenarios 2 and 3 (see below). Table 1 reports the detected putative QTLs. Both MGLAD-LASSO and MG-LASSO analyses correctly detected four or five QTLs, indicating that their performances were similar on the normally distributed traits. Comparing the QTL decision rules, the stability selection and multiple-split testing seemed to detect slightly different sets of QTLs, and none of them produced any false positive.

Table 1 The results from the analysis of original simulated QTLMAS data, including the detected significant markers, their stability selection probabilities or P-values (in brackets) and the closest true simulated QTLs
Full size table

Scenario 2: missing data

Missing phenotype data is an important issue in multiple traits or longitudinal studies. A common situation is that the missing values only occur at a small fraction of traits or time points for one individual. In this case, simply deleting these individuals with few missing values is a pity thing to do, and may result in losing essential information from the data. Here, we investigate how to use MGLAD-LASSO to simply handle the missing data problem in multivariate data. In the QTLMAS2009 phenotype data, 5% of individuals (corresponds to 50 individuals) were randomly chosen, and for each individual, the items were specified as missing values at one or two randomly selected time points. We assume that these simulated data points are missing completely at random. Two different approaches were used to impute once the missing data before the LASSO analysis. First, we applied a quadratic polynomial function to ‘predict’ the values of the missing data points based on known observations of each individual. Alternatively, we replaced all the missing points by an extreme value (say 1000), and the missing data can then be interpreted as outliers. Note that the original scale of the data is from 2 to 40. The simulation was replicated 50 times (in each replication, 50 individuals were randomly selected to simulate some missing items). The performance of MGLAD-LASSO and MG-LASSO were evaluated by the following two quantities calculated over the 50 replications: (i) the frequency of each QTL being correctly identified which measures the statistical power, (ii) the average number of false positive markers measuring the ability of controlling the type I error. Results are shown on Tables 2 and 3 for the two imputed data sets, respectively.

Table 2 In the QTLMAS phenotype data, 50 individuals were simulated with one or two missing items
Full size table
Table 3 In the QTLMAS phenotype data, 50 individuals were simulated with one or two missing items
Full size table

When the missing data were imputed by using quadratic polynomial functions (Table 2), both the MGLAD-LASSO and MG-LASSO methods were able to detect the same set of QTLs as in the complete data case (cf. Table 1), and well control the false positives. This is not surprising, because the phenotype trajectories were originally simulated following monotonic logistic curves and the quadratic polynomial functions can provide accurate prediction to those missing values.

When the missing items were filled by an extreme value (Table 3), MG-LASSO failed to correctly detect any QTL, because it is not robust to the outliers. However, MGLAD-LASSO was still able to find those QTLs with high statistical power, indicating that those artificial outliers do not affect the MGLAD-LASSO analysis. Therefore, in addition to some conventional phenotype imputation methods (Guo and Nelson, 2008), simply filling the missing data with extreme values may also serve as a reasonable approach for pre-processing the phenotype data before the MGLAD-LASSO analysis.

Scenario 3: non-normally distributed data

On the basis of the simulated QTLMAS2009 marker information, we re-simulated five correlated quantitative traits, which follow a non-normal distribution. In detail, we simulated five QTLs exactly at markers 35, 98, 216, 291 and 338. The additive effects of these five QTLs were simulated from a normal distribution with mean 1 and variance 0.25 on each of the five traits. The intercept (population mean) effects were simulated from a normal distribution with mean 10 and variance 1. The residual errors were simulated from a multivariate Student’s t-distribution , with degree of freedom v=1 (in this case, the multivariate Student’s t-distribution becomes a multivariate Cauchy distribution) and scale matrix

This simulation was again repeated 50 times and the average performances of the two methods are shown in Table 4. The MGLAD-LASSO method was able to detect all the five simulated QTLs with higher frequencies than the MG-LASSO, indicating that MGLAD-LASSO is more robust against the mis-specification of the model likelihood. However, MGLAD-LASSO and MG-LASSO performed rather similarly in terms of controlling the false positives. To better evaluate the ability of the MGLAD-LASSO/MG-LASSO methods on controlling false positives, we further simulated a null data set with only the intercept term but no QTL effects (repeated 50 times), and the residual errors following the same multivariate Student’s t-distribution as above. Again, all the approaches produce low number of false positives (Table 5). Our observations are in line with some earlier published simulation studies to evaluate the performance of a univariate Bayesian robust method (Yang et al., 2009). When comparing the QTL decision rules, the conservative multiple-split test outperformed the stability selection by giving less false positives.

Table 4 The analysis of replicated data of the non-normally distributed phenotypes simulated based on the QTLMAS marker information
Full size table
Table 5 Simulation study under the null model based on the QTLMAS marker information: the average number of wrongly selected QTLs (false positives) over 50 replications
Full size table

Analysis and results: sugar beet data

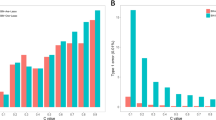
The study is based on 924 diploid elite sugar beet inbred lines, with each line having two replications at one to seven locations in the year 2008. For simplicity, only one replication at each line was selected, and, therefore, there are exactly 924 individuals distributed over 13 locations being used in our analysis. Originally, six quantitative traits were under evaluation including three yield-related traits: white sugar yield (t ha−1), sugar content (%), root yield (tha−1); and three quality-related traits: potassium content (K, mM), sodium content (Na, mM) and α-amino nitrogen content (N, mM). Würschum et al. (2011) performed a single-trait association mapping separately on each of the six traits. In our analysis, we performed the multiple-trait analysis simultaneously on the three yield-related traits including white sugar yield, sugar content and root yield. The histograms of the three yield-related traits are shown in Figure 1. The distribution of sugar content clearly departs from the normal distribution. Furthermore, 677 SNP markers were genotyped. These SNPs were randomly distributed across the sugar beet genome with an average marker distance of 1 cM.

Figure 1
figure 1

The histogram of three yield-related traits including white sugar yield (WSY), sugar content (SC) and root yield (RY) in the sugar beet data set.

Full size image

The pre-processing of the data was done as follows. First, the phenotypes of white sugar yield, sugar content and root yield were standardized to have zero mean and unit variance, so that they are roughly on the same scale. Second, for the genotype data, a marker was excluded from the analysis if its minor allele frequency was <0.05 or the missing data rate was l>0.1. For each of the remaining markers, as the missing genotype rates were generally very low, the missing genotypes were simply imputed by the mean of known genotypes at the same position. Furthermore, like in the QTLMAS simulated data example, only one marker was kept in data to represent a group of highly correlated markers (with pairwise correlation >0.9). After these steps, a number of 481 markers were used in the association analysis. In the multivariate LASSO analyses, the 13 locations were considered as extra covariates, and they were just treated in the same way as the markers and were subjected to variable selection.

The results are summarized in Table 6. The MG-LASSO with either QTL decision rules detected markers 192, 259, 289, 349, 418 and 553 as putative QTLs. Most of the putative QTLs have also been found by a linear mixed model-based association mapping method in Würschum et al. (2011), except the one at marker 289. On the other hand, the MGLAD-LASSO was able to detect putative QTLs including markers 27, 162, 184, 259, 349 and 411. Except the markers 27 and 162, all the others were also reported in Würschum (2011).

Table 6 The results from the analysis of the three yield-related traits: white sugar yield, sugar content and root yield of the sugar beet data, including the detected QTLs, their stability selection probabilities or P-values (in brackets)
Full size table

Interestingly, the MG-LASSO detected 9–13 location covariates as significant in addition to those putative QTLs, but MGLAD-LASSO only identified three location variables. This may indicate that the non-normality of the trait distributions under study was mainly caused by those location factors. The MG-LASSO needs to include the locations into the model to weaken the non-normality in the phenotype data. To illustrate this point, we used the following single-trait mixed-effect model to fit each of the three traits (in the original scale) separately:

where yij is the phenotype of ith sugar beet line at the jth location, lj is the effect of the jth location and eij is the residual term. Figure 2 shows the distribution of the estimated residuals . Clearly, after the correction of location effects, residuals become more normally distributed compared with the original phenotypes. On the other hand, MGLAD-LASSO does not need to include location variables because it is robust against skewedly distributed data. Thus, the MGLAD-LASSO method will be particularly suitable for data sets collected from multiple sources like the sugar beet data, but without having any information on which group/location/environment an individual belongs to.

Figure 2
figure 2

The histogram of the estimated residuals of the three yield-related traits including white sugar yield (WSY), sugar content (SC) and root yield (RY) in the sugar beet data set, after correcting the location effects by a linear mixed model.

Full size image

Discussion

This paper introduces a multivariate robust regression approach for QTL mapping of multiple traits. The method is developed on the basis of the well-known LASSO (Tibshirani, 1996) and group LASSO methods (Yuan and Lin, 2006) for shrinkage estimation of marker effects, and stability selection (Meinshausen and Bühlmann, 2010) and/or multiple-split test (Meinshausen et al., 2009) for formally judging QTLs. Consequently, the method can be used to do simultaneous estimation and testing of thousands of markers. Different from the standard MG LASSO (MG-LASSO), which assumes the residual terms to follow a multivariate normal distribution, our LAD LASSO (MGLAD-LASSO) assumes the residuals to follow a multivariate Laplace distribution, which has heavier tails compared with the normal distribution. Because of this, MGLAD-LASSO should be a more appropriate method for a data set with phenotypic outliers or a data set with skewedly distributed traits. Our simulation studies clearly demonstrate that MGLAD-LASSO is superior to the MG-LASSO in terms of correctly detecting more QTLs for such kind of data sets. A drawback of the MGLAD-LASSO method is its high computational cost. For a data set with 924 markers, MGLAD-LASSO implemented by R-MNM package costs several minutes for a single run, but MG-LASSO implemented by the R-glmnet package only costs several seconds.

Nevertheless, MGLAD-LASSO is a suitable tool for analyzing some normally distributed traits as well. An interesting application of MGLAD-LASSO is on multiple traits with missing phenotype data. As shown in our simulation studies, it is possible to use a very simple strategy to handle such a missing data problem in which all the missing items are filled by some extreme values and treated as outliers. The MGLAD-LASSO method is resistant to those extreme values filled for missing items, and it provides reasonable parameter estimation and testing based on all the available data. Our suggestive strategy for handing missing phenotype data by using MGLAD-LASSO is connected to a missing data technique named the maximum-likelihood estimation using observed data likelihood (Baraldi and Enders, 2010), where they proposed to build a specific-likelihood function and do the inference on the basis of all the available data without treating any missing data.

A relevant research topic connected to association mapping of using multiple-locus models is genomic selection, which aims to estimate and predict the genomic breeding values based on a dense marker set instead of identifying any specific quantitative trait locus (Meuwissen et al., 2001). Previous studies demonstrate that LASSO can also be used for genomic selection (Li and Sillanpää, 2012; Xu et al., 2014). With simulation studies, Estaghvirou et al. (2014) showed that performance of standard genomic selection methods might be significantly affected when the data have outlying phenotypic observations. In addition, a multiple-trait genomic selection method might be superior to a single-trait genomic selection method in some circumstances (Yi and Jannink, 2012; Hayashi and Iwata, 2013). All these evidences indicate that our MGLAD-LASSO approach may potentially be an appropriate tool for genomic selection as well, especially when the outliers or missing items exist in the phenotype data. Further investigation is needed to measure the usability of the MGLAD-LASSO in genomic selection.

Our current MGLAD-LASSO method still has some room for improvement from the following three perspectives. First, the current fixed point algorithm for finding MGLAD-LASSO solutions is easy to derive, and should work for moderate-sized data sets with thousands of markers and individuals. However, it may not be efficient for genome-wide data sets with very large number of markers and individuals which have become more and more common recently. For improvement, more efficient algorithms are needed to be developed for MGLAD-LASSO such as the coordinate descent algorithm, which has been available for single-trait LAD-LASSO (Wu and Lange, 2008). Second, the current MGLAD-LASSO method assumes the model residual terms to follow a symmetric Laplace distribution. However, in reality, the distributions of some quantitative traits may show non-symmetric pattern, such as ‘sugar content’ in the sugar beet data set (see Figure 1). Quantile regression (Koenker, 2005), a generalization of the LAD regression, may provide better description of such non-symmetric distributed data. The quantile regression with LASSO penalty has been available for analyzing single response/trait (Li et al., 2010), and potentially its multivariate version can be developed. Third, our current method describes the correlation among traits in the marker effects part by using group LASSO penalty, but assumes the residuals to be independent. It has been shown that the modeling of residual covariance in the standard multivariate LASSO regression may have some advantages (Rothman et al., 2010). In principle, it is possible to include the residual covariance in our MGLAD-LASSO model as well, but the computation needs to be done by more sophisticated algorithms. This can be taken as one of our future research direction.

Data Archiving

There were no data to deposit.