Aripiprazole (APZ) is a second-generation antipsychotic, known as a typical antipsychotic. This drug is effective in a wide range of psychotic disorders such as schizophrenia1. It can also serve as a mood stabilizer in the treatment of bipolar disorder2,3,4. APZ has been approved by the Food and Drug Administration (FDA) for the treatment of mixed episodes associated with bipolar disorder and acute manic. It appears that functional selectivity at D2 receptors may contribute to the antipsychotic effects of APZ5,6,7. As a typical antipsychotic compound, APZ selectively binds targeting serotonin and central dopamine D2 receptors which can be effective in the treatment of cognitive and negative symptoms of schizophrenia1,7. Based on previous studies, APZ can prevent the activation of microglia by reducing the inflammatory cytokines8,9,10. APZ can be used in the treatment of depression due to its effect on microglia activities and anti-inflammatory behavior. However, low bioavailability of Aripiprazole due to its poor aqueous solubility has significantly limited the development of APZ-based drugs and their therapeutic effects on depression8,11.

Drugs with poor water solubility often show poor oral bioavailability and limited absorption rate. The improvement of the absorption, solubility, and permeability of poorly water-soluble drugs is one of the major research topics12. The dissolution rate of the pharmaceutical compounds increases by decline of their particle size. Several conventional methods such as grinding, sieving, spray drying, and re-crystallization can be used to reduce the particle size. Each of these methods has their own drawbacks. In the last decade, supercritical fluids (SCF) technology has been employed as a micronization process to serve as an alternative to traditional methods. Researchers have used supercritical fluids as solvent or anti-solvent in the extraction processes, solution-enhanced dispersion, and solutions/suspensions rapid expansion methods13,14,15,16,17,18,19,20,21,22. In addition to its moderate critical point (304.1 K as temperature and 7.38 MPa as pressure), SC-CO2 enjoys non-polluting nature, non-flammability, non-explosiveness, and accessibility in high purity15,23,24,25,26. In the process of nanoparticle production, the drug solubility in supercritical fluid is the main parameter as it determines the feasibility of supercritical methods. This parameter also specifies the role of SCF as solvent, anti-solvent, or reaction medium27,28. The RESS-based processes are generally employed to prepare nanoparticle drugs with high SC-CO2 solubility, in contrast, anti-solvent procedures are suitable in the preparation of the drug with low solubility29,30,31,32. A wide range of drugs with different SC -\({\mathrm{CO}}_{2}\) solubility levels have been recently examined25,33,34,35. Moreover, various approaches have been developed to measure the drug solubility in SC–\({\mathrm{CO}}_{2}\), among which, gravimetric36,37,38,39, spectrometric40,41,42, chromatographic43,44, and miscellaneous46 methods can be mentioned. Modeling methods can also help to investigate the solubility of pharmaceuticals in SC–\({\mathrm{CO}}_{2}\) with far lower time and costs and no need for complex equipment13.

Various mathematical models have been developed to assess the solubility of different compounds in SC–\({\mathrm{CO}}_{2}\). These methods can be categorized into several groups including equation of state (EoS), empirical and semi-empirical models, expanded liquid models, square support vector machine (LS-SVM), and artificial neural network (ANN) techniques45,47. Empirical and semi-empirical models are capable of correlating the experimental solubility data to operating conditions such as temperature, pressure, and the ratio of the cosolvents to the supercritical solvent density. No need for pure solid properties is the greatest advantage of these models23,46,47. The EoS are classified into two categories: cubic EoS, such as the Peng-Robinson (PR)50 and the Soave- Redlich- Kowang (SRK)51, and non-cubic EoS. Activity coefficient-based models like modified Wilson models and universal quasi-chemical models (UNIQUAC) can be used to correlate the solubility data. The physicochemical properties of solid solutes are required in both EoS-based and activity coefficient models whose experimental measurement is a challenging and complex task. Therefore, some methods have been developed to determine the properties of solute molecules48. Empirical and semi-empirical models (Chrastil49, Bartle et al.46, Kumar and Johnston (K-J)53, Garlapati et al.54, Menden -Santiago & Teja (MST)55, Sodeifian et al.33, Jouyban et al.56) and expanded liquid models (universal quasi chemical, modified Wilson's model)50,51 have been utilized to determine the solubility of various drugs in SC–\({\mathrm{CO}}_{2}\).

In this study, the APZ solubility in SC-\({\mathrm{CO}}_{2}\) was experimentally assessed at various pressures (12–30 MPa) and temperatures (308–338 K). The results were correlated with several models including Chrasti, Bartle et al. (K-J), MST, Sodeifian et al. Jouyban et al. and modified Wilson's model. The accuracy of these models in the correlation of APZ solubility was explored by calculating and comparing average absolute relative deviation (AARD %) and adjusted correlation coefficient (\({R}_{adj}\)).

Materials and methods

Materials

A sample of APZ (form II) with CAS number of 9-12-129722 and purity of 99% was purchased from Tofigh Daru Pharmaceutical Company (Tehran, Iran). Carbon dioxide (CAS number 124-38-9) with a purity of 99.98% was also supplied from Oxygen Novin Company (Shiraz, Iran). Methanol (CAS number 67-56-1) with minimum purity of 99.9% was also provided from Merck (Germany).

Physical and critical characteristics

The solubility of APZ in SC-\({\mathrm{CO}}_{2}\) was quantified by thermodynamic investigations using appropriate group participation methods. The melting point (\({\mathrm{T}}_{\mathrm{m}}\)) was determined by DSC analysis while the boiling point (\({\mathrm{T}}_{\mathrm{b}}\)), critical pressure (\({\mathrm{P}}_{\mathrm{c}}\)), and critical temperature (\({\mathrm{T}}_{\mathrm{c}}\)) were evaluated by the Marrero and Gani contribution method59. To calculate these features, the molecular structure of APZ was broke down to 10CH2, 6CH (cyclic), 2C (cyclic), 2C-CL (cyclic), 2N (cyclic), 1C-O (cyclic), 1C-NH (cyclic), 1C, and 1O (cyclic). The molar volume (\({V}_{S}\)) and Grain Watson52, sublimation pressure (\({\mathrm{P}}_{\mathrm{S}}\)), and the corresponding modes of Ambrose-Walton53 factor (ω) were determined according to the Immirzi-Perini method54, as listed in Table 1.

Table 1 The solute Aripiprazole structure and the respective physic-chemical features.
Full size table

Experimental setup and solubility assessment

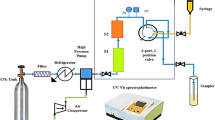
The experimental setup of this device includes a \({\mathrm{CO}}_{2}\) cylinder (E-1), valve (E-2), filter (E-3), refrigeration unit (E-4), high-pressure pump (E-5), air compressor (E-6), Needle valve (E-7), oven (Memmert) (E-8), equilibrium cell (E-9), back pressure valve (E-10), metering valve (E-11), collection vial (E-12), control panel (E-13), syringe (E-14), digital pressure transmitter (WIKA, Germany, code IS-0-3-2111), pressure gauge (WIKA, Germany, code EN 837-1), a digital thermometer, and 1.8-inch pipe and fittings (Fig. 1).

Figure 1
figure 1

Schematic diagram of the SC-CO2 solubility measurement used in this research.

Full size image

The high-pressure system was made of stainless steel 316. In a typical process, \({\mathrm{CO}}_{2}\) first passed through a 1 µm filter to be purified on its way to the refrigerator, at which, its temperature was reduced to – 15 °C for liquefaction. The pressure of liquid \({\mathrm{CO}}_{2}\) was then increased up to 12–30 MPa. Such a high pressure can be controlled through a reciprocating pump. APZ (1 g) and liquid \({\mathrm{CO}}_{2}\) were then mixed and homogenized by a magnetic stirrer (100 rpm) in a cell placed in an oven for 120 min. The static time, drug content, and purity were checked by some preliminary tests. At the end of the static time, 600 μL of saturated SC-\({\mathrm{CO}}_{2}\) was loaded into the injection loop through a three-valve two-position valve. By opening the injection valve, the sample collected inside the vial was released with 5 ml of methanol which had been already loaded. Subsequently, the vial was washed by the syringe pump which injected 1 ml of methanol. The drug content of the obtained sample was evaluated by a spectrophotometer at a wavelength of 254 nm. A calibration curve was also used to estimate the concentration of the solutes. A set of standard solutions were obtained through diluting the stock solutions. Drug solubility in SC-\({\mathrm{CO}}_{2}\) can be calculated at various pressures and temperatures using the following equations:

$${y}_{2}=\frac{{n}_{solute}}{{n}_{solute}+{n}_{{CO}_{2}}}$$
(1)
$${\mathrm{n}}_{\mathrm{solute}}=\frac{{\mathrm{C}}_{\mathrm{s}}\times {\mathrm{V}}_{\mathrm{s}}}{{\mathrm{M}}_{\mathrm{S}}},\mathrm{and}$$
(2)
$${\mathrm{n}}_{{\mathrm{CO}}_{2}}=\frac{{\mathrm{V}}_{\mathrm{l}}\times\uprho }{{\mathrm{M}}_{{\mathrm{CO}}_{2}}} ,$$
(3)

where \({\mathrm{n}}_{\mathrm{solute}}\) and \({\mathrm{n}}_{{\mathrm{CO}}_{2}}\) denote the number of moles of the solute and \({\mathrm{CO}}_{2}\), respectively, \({\mathrm{C}}_{\mathrm{S}}\) shows the solute concentration (\(\mathrm{g}.{L}^{-1}\)) based on the calibration curve. \(\mathrm{Vs}(\mathrm{L})\) and \(\mathrm{Vl}(\mathrm{L})\) represent the volumes of the sampling vial and collection ring, respectively. \({\mathrm{M}}_{\mathrm{S}}\) and \({\mathrm{M}}_{\mathrm{CO}2}\) stand for the molecular mass of the solute and \({\mathrm{CO}}_{2}\), respectively. Equation (4) expresses the equilibrium solubility of the solute (S) in SC-\({\mathrm{CO}}_{2}\):

$$\mathrm{S}=\frac{\uprho \times {\mathrm{M}}_{\mathrm{solute}}\times {\mathrm{y}}_{2}}{{\mathrm{M}}_{{\mathrm{CO}}_{2}}\times \left(1-{\mathrm{y}}_{2}\right)} .$$
(4)

Results and discussion

Experimental data

The solubility of APZ in SC-\({\mathrm{CO}}_{2}\) was examined at different temperatures (308–338 K) and pressures (12–30 MPa). The measurements were carried out in triplicates to reduce the error. Data of APZ solubility in SC-CO2 including its mole fraction (y), density (ρ), solubility (S), and expanded uncertainty are also presented in Table 2. Accordingly, the highest APZ mole fraction \((1.036\times {10}^{-5}\)) was detected at 338 K and 30 MPa whereas the lowest value (\(1.830\times {10}^{-6}\)) was recorded at 338 K and 12 MPa. The solubility showed an ascending trend with increasing the pressure at high temperatures. As the pressure rises, the density of SC-\({\mathrm{CO}}_{2}\) increases which enhances the strength of the solvent. The solvent density and the vapor pressure of the solution are the main factors in the solubility enhancement. Based on Fig. 2, the solubility curve showed a crossover region. Temperature generally exhibited a dual effect on drug solubility in SC-CO2 under controlled SC-CO2 density and drug vapor pressure. The solubility of APZ in SC-CO2 decremented in the pressure range of 12–18 MPa by enhancing the temperature. At pressures above 18 MPa, the solubility rose with temperature elevation. The crossover region for APZ ranged from 12 to 18 MPa. At pressures lower than 18 MPa, the effect of density was predominant as the solubility increased by temperature reduction. However, at pressures above 18 MPa, solubility rose with temperature increment due to the predominance of the influence of the vapor pressure of the drug. The impact of temperature on carbon dioxide density and vapor pressure of solute was reported by several articles with similar values of the SC − CO2 pressure crossover region for Nystatin55, Clonazepam56 and famotidine57. These transitions can be attributed to temperature-induced density changes in carbon dioxide and vapor pressure changes in solutes. The crossover pressure was investigated in several articles, which proposed some methods to predict the crossover pressure region58,59,60. The crossover region varies depending on the critical properties of the solute, such as its sublimation pressure, sublimation enthalpy, partial molar enthalpy, and molar volume. Thus, the pressure range of 12–18 MPa was introduced as the crossover region for APZ drug (Fig. 2).

Table 2 The APZ solubility at distinctive operational conditions (12–30 MPa) and (308–338 K).
Full size table
Figure 2
figure 2

Experimental solubility of APZ in SC-CO2 at various pressures and temperatures. (a) Solubility according to pressure and (b) solubility according to density.

Full size image

Semi-empirical models

Semi-empirical models such as Chrastil49, Bartle et al.61, K-J62, MST63, Sodeifian et al.33, and Jouyban et al.64 were used for the correlation of the solubility of APZ. Table 3 lists the equations of the semi-empirical models. Chrastil49 proposed an equation for the solid solutes based on the SCF density and absolute temperature (\({\mathrm{a}}_{2}=\frac{{\Delta \mathrm{H}}_{\mathrm{t}}}{\mathrm{R}} )\), in which, the adjustable parameter of \({a}_{2}\) is a function of the total heat. R shows the global gas constant and \({\Delta \mathrm{H}}_{\mathrm{t}}\) represents the total heat of mixing. The vaporization enthalpy (\({\Delta \mathrm{H}}_{\mathrm{vap}}\)) can be determined by the model proposed by Bartle et al.61. According to the Hess' law, the solvation enthalpy \(\left({\Delta \mathrm{H}}_{\mathrm{sol}}\right)\) can be defined as the difference between \({\Delta \mathrm{H}}_{\mathrm{t}}\) and \({\Delta \mathrm{H}}_{\mathrm{vap}}\). Sodeifian et al. proposed a semi-empirical model \({a}_{0}-{a}_{5}\) and introduced six adjustable parameters. In 1998, K-J62 presented a density-based semi-empirical model for the correlation of the solid solubility in SCF. They expressed the relationship of \({a}_{2}\) with \({\Delta \mathrm{H}}_{\mathrm{t}}\) through \({\Delta \mathrm{H}}_{\mathrm{t}}=\frac{{\mathrm{a}}_{2}}{\mathrm{R}}\). A simple linear equation is shown by MST model for consistency of solid solubility in SCF.

Table 3 The semi-empirical models exploited in the present study.
Full size table

Semi-empirical models of Chrastil49, Sodeifian et al.33, K-J62, MST63, Bartle et al.33, and Jouyban et al.64 have three, six, three, three, three, and six parameters, respectively. The mentioned models were used from the Simulated Annealing algorithm for optimization. The adjustable parameters of the relevant statistical measures were obtained in terms of AARD% and \({R}_{adj}\) for the \({\mathrm{CO}}_{2}\)-APZ binary system using the density-based models as listed in Table 4.

Table 4 Diverse parameters of APZ—CO2 binary system, as obtained using models proposed by Chrastil, Bartle et al. Kumar and Johnston, MST, Sodeifian et al. and Jouyban et al.
Full size table

The average absolute relative deviation (AARD %) was used to assess the precision of the models:

$$AARD\%=\frac{100}{{N}_{t}-Z}\sum_{i=1}^{{N}_{t}}\frac{\left|{y}_{2}^{calc}-{y}_{2}^{exp}\right|}{{y}_{2}^{exp}}$$
(5)

In the above equation, Z represents the number of adjustable parameters of each model, \({N}_{t}\) shows the number of data points in each set, and \({y}_{2}\) denotes the mole fraction solubility. The correlation coefficient adjusted by \({\mathrm{R}}_{\mathrm{adj}}\) is defined as follows:

$${R}_{adj}=\sqrt{\left|{R}^{2}-\left(Q\left(1-{R}^{2}\right)/\left(N-Q-1\right)\right)\right|}$$
(6)

While the correlation coefficient is represented by \({R}^{2}\), the number of data points in each set is shown by N. Q also denotes the number of independent variables in each equation.

The AARD% values were 7.90, 10.73, 5.90, 9.30, 5.89, and 4.39 for Chrastil, Bartle et al., K-J, MST, Sodeifian et al., and Jouyban et al., respectively. The models proposed by Jouyban et al. and Sodeifian et al. showed the best performance in predicting the solubility of APZ with respective AARD% values of 4.39 and 5.89%. Jouyban et al. model exhibited the best correlation compared to others. The linear equation of Jouyban et al. is generally more suitable for predicting the solubility of this type of drug compared to the model proposed by Bartle et al. Other semi-empirical models offered acceptable predictive accuracies. The results also revealed the higher precision of the Chrastil model in predicting the solubility data with \({\mathrm{R}}_{\mathrm{adj}}\)=0.994. Figure 3 compares the experimental solubility with those calculated by the density-based models.

Figure 3
figure 3

A comparison of experimental (points) and modeled (lines) values of APZ solubility based on semi-empirical models at different temperatures.

Full size image

Figure 4 demonstrates the self-consistency of experimental data of APZ solubility with Chrastil, Bartle et al., MST, and K-J models. The model is acceptable in self-consistency tests if all the solubility data obtained at different temperatures are located on the \(45-\mathrm{degree}\) line. The test results of the mentioned semi-empirical models suggest the consistency of the measured solubility values.

Figure 4
figure 4

The self-consistency results obtained for four semi-empirical models. The lines suggest the linearity of the models.

Full size image

Table 5 lists the calculated enthalpy for APZ in SC-\({\mathrm{CO}}_{2}\). The Chrastil model shows the approximate total heat of \(30\mathrm{ KJ}.{\mathrm{mol}}^{-1}\). Based on Bartle’s model, the enthalpy of vaporization was \((48.73\mathrm{ KJ}.{\mathrm{mol}}^{-1})\). Solvation heat (\({\Delta \mathrm{H}}_{\mathrm{sol}}\)) was equal to \(18.73\mathrm{ KJ}.{\mathrm{mol}}^{-1}\) based on the difference between \({\Delta \mathrm{H}}_{\mathrm{vap}}\) and \({\Delta \mathrm{H}}_{\mathrm{t}}\).

Table 5 The vaporization (ΔHvap), approximated total (Ttotal), and solvation (ΔHsol) enthalpy for APZ.
Full size table

Modified Wilson model

Since the solid solubility in the supercritical phase is very small, we can assume to be at infinite dilution condition. Consequently, the activity coefficient of the solid solute is the one at infinite dilution (\({\gamma }_{2}^{\infty }\)) and the density of the solution is that of the pure solvent. Therefore, the solubility equation is obtained:

$${\mathrm{y}}_{2}=\frac{1}{{\upgamma }_{2}^{\infty }}\mathrm{exp}\left[\frac{{-\Delta \mathrm{H}}_{2}^{\mathrm{f}}}{\mathrm{R}}\left(\frac{1}{\mathrm{T}}-\frac{1}{{\mathrm{T}}_{\mathrm{m}}}\right)\right]$$
(7)

\({-\Delta \mathrm{H}}_{2}^{\mathrm{f}}\) is the enthalpy of fusion and Tm is the melting point temperature of the solid solute.

Gibbs excess energy is defined according to the following formula for the binary system. Wilson’s model has two variable parameters \(({\lambda {\prime}}_{12}and{\lambda {\prime}}_{21}\)) which are the difference of intermolecular interaction energies of the molar volume of supercritical carbon dioxide. Moreover, \({\vartheta }_{1 }and {\vartheta }_{2}\) are dependent values due to the low solubility of the solute in the SC-CO2 where \({\vartheta }_{1 }and {\vartheta }_{2}\) are the molar volumes of the SCF (expanded liquid) and the solid solute respectively. The following equation can be used to determine the activity coefficient:

$$\mathrm{ln}\,{\gamma }_{2}^{\infty }=1-{\Lambda }_{12}-\mathrm{ln}{\Lambda }_{21}$$
(8)

\({\vartheta }_{1 }\mathrm{and }{\vartheta }_{2}\) can be defined under infinite dilution conditions:

$${\Lambda }_{12}={\vartheta }_{2}{\rho }_{cl}{\rho }_{r}exp\left(-\frac{{\lambda {^\prime}}_{12}}{{T}_{r}}\right)$$
(9)
$${\Lambda }_{21}=\frac{1}{{\vartheta }_{2}{\rho }_{cl}{\rho }_{r}}exp\left(-\frac{{\lambda {^\prime}}_{21}}{{T}_{r}}\right)$$
(10)

\({\rho }_{r}\) is the reduced density of the solvent (SCF) equal to \(\rho\) /\({\rho }_{cl}\), where \({\rho }_{cl}\) is its critical density and the dimensionless energies of interaction are as follow:

$${\lambda {\prime}}_{12}=\frac{{\lambda }_{12}}{R{T}_{C1}}$$
(11)
$${\lambda {\prime}}_{21}=\frac{{\lambda }_{21}}{R{T}_{C1}}$$
(12)

A linear equation can be defined between molar volume and reduced density to capture the effect of high pressure on the model:

$${\vartheta }_{2}=\alpha {\rho }_{r}+\beta$$
(13)

\({{\lambda {\prime}}_{12},\lambda {\prime}}_{21}, \alpha ,\mathrm{ and }\beta\) were obtained by the model.

Using the extended liquid theory, the modified Wilson model was utilized for optimization of the parameters of the model of APZ solubility in SC-CO2. Table 6 summarizes the parameters of the modified Wilson model (\(\alpha ,\beta ,{\lambda {\prime}}_{12},{\lambda {\prime}}_{21}\)). A comparison of experimental and modeled data (Fig. 5) confirmed the accuracy of the modified Wilson model. Based on Table 6, \({\lambda {\prime}}_{21}\) is smaller than \({\lambda {\prime}}_{12}\) as also reported in previous studies27,34,50,51,65.

Table 6 Modified Wilson model parameters for solubility of APZ in SC-CO2.
Full size table
Figure 5
figure 5

Experimental data (point) and calculated (line) solubility of APZ in SC-CO2 based on the modified Wilson model.

Full size image

Conclusion

APZ solubility was evaluated at different pressures (12, 15, 18, 21, 24, 27, and 30 MPa) and temperatures (308, 318, 328, and 338 K). The molar fraction of APZ in SC-CO2 varied from \(1.83\times {10}^{-6}\) to \(1.036\times {10}^{-5}.\) The lowest and highest molar fractions of APZ were detected at a constant temperature of 338 K and pressures of 12 and 30 MPa, respectively. Six semi-empirical models (Sodeifian et al., Jouyban et al., Chrastil, Bartle et al., MST, K-J), and an extended liquid theory (modified Wilson model) were employed for the correlation of the experimental solubility data. The precision of the models was explored in terms of AARD% and \({\mathrm{R}}_{\mathrm{adj}}\). Accordingly, the modified Wilson model (AARD% = 6.82) and the semi-empirical models of Chrastil (AARD% = 7.90), Bartle et al. (AARD% = 10.73), Jouyban (AARD% = 4.39), MST (AARD% = 9.30), Kumar Johnston (AARD% = 5.90), Sodeifian et al. (AARD% = 5.89), Jouyban et al., and Sodeifian et al. with six adjustable parameters showed the best correlation among density-based models, reflecting the ability of this model to correlate solubility data. Such satisfactory correlation results of the semi-empirical models also show the self-consistency of the experimental findings. The models of Chrastil and Bartle et al. were also applied to determine the enthalpy of vaporization and solvation.