Main

Computers are useful because they are versatile. Changing the problem to be solved amounts to reconfiguring inputs to the processor, that is, to reprogramming it. In a classical computer, a program is ultimately decomposed into sequences of operations implemented with logic gates. The explosion of interest in quantum information science coincided with the realization that a similar decomposition exists for quantum processors3,4,5; arbitrary operations on a multiqubit system can be broken down into sequences of discrete operators—‘quantum gates’. As with its classical counterpart, a programmable quantum computer is more versatile than one designed for a fixed task.

Ease of implementation can favour certain decompositions of quantum operations, for example, those based on arbitrary single-qubit gates and a single entangling two-qubit gate4,5. As realizing gates acting on two or more qubits tends to be more experimentally challenging7, much attention has been focused on using them optimally in the creation of entanglement10 and on finding decompositions minimizing the number of times they are applied6,11,12,13,14. Some well-chosen operations can be carried out with two or fewer applications of two-qubit gates, but these form an infinitesimal subset in the space of two-qubit operations12. For a two-qubit system with a maximally entangling two-qubit gate, three applications of this gate, when combined with applications of arbitrary single-qubit gates, are sufficient for universality11. Here we present and characterize a universal quantum processor that can produce any desired two-qubit unitary transformation when programmed with 15 classical inputs10,12. As opposed to programming a fixed gate array with quantum inputs15, these classical inputs select particular single-qubit quantum gates and allow deterministic—rather than probabilistic—computation.

The decomposition of a given operation depends on the available gate set. Our choice of a universal gate library consists of single-qubit gates and one maximally entangling two-qubit gate. The single-qubit gates are rotations

in the computational basis |1〉≡(1,0),|0〉≡(0,1). Here, σx, σy and σz are the Pauli matrices. The single-qubit gates have variables θ, φ and φz that can take any value from 0 to 2π. The entangling two-qubit gate is

and operates on the basis |11〉, |10〉, |01〉, |00〉. Here, indicates the tensor product and .

With this gate library, the circuits shown in Fig. 1 can be used to implement arbitrary unitary transformations on one qubit (Fig. 1a) and two qubits (Fig. 1b). The single-qubit operation is characterized by three degrees of freedom and may be decomposed into the matrix product Rz(φz)·R(θ,φ). Each two-qubit unitary transformation is described by 15 degrees of freedom10,12. The group of all such transformations can be divided into subsets that are equivalent up to single-qubit operations. Such subsets are called local equivalence classes16 because local operations can map among all members of the class. Each local equivalence class can be described by three parameters10. Given a unitary transformation U, we decompose it into . Here, V is in the same local equivalence class as U and is in a special form that requires fewer gates on our processor. A and C are single-qubit operations on one of the qubits, and B and D are single-qubit operations on the other.

Figure 1: Components for universal computation.
figure 1

a,b, Circuit diagrams for arbitrary unitary transformations on one (a) and two (b) qubits. The operations for each circuit are implemented from left to right, with each line representing one qubit. a also indicates the decomposition used for R(θ,φ). The dashed rectangle in b contains the three degrees of freedom α,β and δ that determine the two-qubit operation’s local equivalence class. The brackets highlight the decomposition of the two-qubit operation U as described in the text: .

Full size image

Determination of the 15 single-qubit-gate parameters is facilitated by working in the so-called magic basis10:

This basis amounts to the Bell states with specific global phases, and we take advantage of two of its convenient mathematical properties. First, single-qubit operations with unit determinant are given in this basis by real matrices that are orthogonal16. Second, two-qubit operations u and v in SU(4) are in the same local equivalence class if and only if u uT and v vT have the same eigenvalues16 (uT is the matrix transpose of u, and we use lower-case letters to represent matrices in the magic basis). The decomposition of a given operation U follows a two-step procedure analogous to that in ref. 14. (See the Methods section for details and Supplementary Information for examples.) Briefly, we first match matrix eigenvalues to find a special element V in the same local equivalence class as U (that is, find α,β and δ, the three degrees of freedom in the dashed rectangle in Fig. 1b). Second, we manipulate real, orthonormal matrix eigenvectors to find the four remaining single-qubit operations required to map between V and U. As the magic basis properties rely on unit matrix determinants, we can implement operations only up to a global phase. Global phases exactly vanish in any observable quantity, so this restriction has no physical relevance.

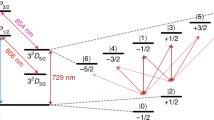
We implement the quantum circuit with trapped ions using techniques applicable for scaling to a larger system9. Each qubit is stored in a pair of energy eigenstates in the 9Be+ 2s 2S1/2 hyperfine manifold. The qubit basis states can be transferred between different pairs of the eight hyperfine levels9. The qubit spends most of its time stored in the (|1〉, |0〉)=(|F=1, mF=0〉, |F=2, mF=1〉) ‘magnetic-field-independent’ manifold, for which the energy splitting has zero first-order dependence on the magnetic field at our chosen value of 0.011964 T, leading to long coherence times (15 s has been measured for a pair of states with a similar second-order field dependence17).

The two 9Be+ ions are stored simultaneously with two 24Mg+ ions in a six-zone linear Paul trap9,18; the ions form a linear chain along the axis of weakest confinement. Coulomb repulsion couples the motion of all four ions such that laser cooling the 24Mg+ ions sympathetically cools all of the ions without destroying the quantum information9,18 stored in the 9Be+ ions. The collective motion of the four ions can be described as the sum of 12 normal modes, four along each of the principal axes. The two-qubit gate uses two modes involving motion along the axis of the ion chain9,18. We spectrally address the 24Mg+ ions to Doppler and resolved-sideband cool these modes to near the quantum ground state of motion9. As the ion spatial order affects the mode frequencies, and because both resolved-sideband cooling and the two-qubit gate require spectral addressing of the modes, we deterministically initialize the ion order18 to 9Be+ –24Mg+ –24Mg+ –9Be+ at the beginning of each experimental sequence.

State preparation and measurement are carried out using resonant laser light that couples the 9Be+ 2s 2S1/2 states to the 2p 2P1/2 and 2p 2P3/2 states19. Projective measurements in the single-qubit computational basis |1〉, |0〉 use a cycling transition9,19. Measurements in other bases are made by first rotating their eigenvectors into the computational basis. A single detection apparatus sequentially measures the two qubits independently9.

The universal gate set above is implemented with laser-induced stimulated Raman transitions19. The two-qubit gate G is a geometric phase gate9,20. The single-qubit gate R(θ,φ) can be produced by driving resonant Rabi oscillations between the qubit states, where the angle θ is controlled by the laser pulse intensity and duration. The phase φ is set by the phase difference between the two Raman light fields at the ion relative to the qubit phase19. It is controlled by means of the phase of a radiofrequency potential applied to an acousto-optic modulator (AOM). The single-qubit gate Rz(φz) advances the qubit phase by φz relative to that of the Raman light fields. It is implemented by retarding the phase of an AOM’s radiofrequency potential for subsequent laser pulses. To individually apply R(θ,φ) to each qubit, time-dependent electric potentials21 divide the four-ion chain into two 9Be+ –24Mg+ pairs and transport them to zones separated by 240 μm. The four applications of R(θ,φ) per qubit in Fig. 1b require four such ion separations and subsequent recombinations—a total information transport of nearly 2 mm per qubit. An AOM placed before the trap directs the laser beams to the relevant ion.

The requirement that single-qubit-gate inputs take any value from 0 to 2π prompts a further decomposition of R(θ,φ). The radiofrequency potentials that control φ and φz are generated by a stable oscillator with easily controllable phase. The variable θ, however, depends on the laser pulse’s intensity, which for technical reasons is not constant for the duration of the pulse. Rather than calibrate this for arbitrary θ, we calibrate a single value, θ=π/2, and decompose R(θ,φ) into

In this way, all 15 inputs to our universal circuit are controlled by shifting the phase of a control oscillator relative to the qubit. The number, duration and spacing of the laser pulses are identical for every U.

To demonstrate the ability of the processor to generate arbitrary unitary transformations, we program it with 160 different randomly chosen operations distributed in SU(4) according to the Haar measure22. (The probability distribution given by the Haar measure is a uniform distribution in the space of unitary matrices.) To characterize our implementation of the 160 operations, we apply each to one of 16 input states formed by the tensor products of and . The assignment of an operation to an input state is random with the constraint that all input states are used an equal number of times. The application of an operation to its input state produces an output density matrix, which we reconstruct using quantum state tomography8,23. This procedure involves nine analysis settings. For each setting, we run the experimental sequence 100 times for a total of 900 runs per unitary transformation. A single run takes approximately 37 ms. We compare the measured output state to the ideal result using the fidelity24, . Figure 2 shows four examples of the output states, and Fig. 3a shows a histogram of the 160 state fidelities. The 160 operations have a mean state fidelity of 〈f〉=79.1(4.5)%, where the error bar is the standard deviation of the measurements. Numerical estimates9 indicate that 3.4% of this distribution arises from statistical fluctuations in photon counts used in state measurement. We attribute the remaining distribution to variability in each operation’s susceptibility to experimental noise. We observe no correlation between output-state fidelity and input state, as demonstrated in Fig. 3b,c. The mean output-state fidelities from operating on the 16 input states are distributed with a standard deviation of 1.5%, as we would expect for the means of ten measurements, which themselves have a standard deviation of 4.5%. The primary fidelity loss mechanisms are per-cent-level intensity fluctuations in the Raman light fields9 and spontaneous emission25; the fidelities observed here are consistent with those demonstrated previously9 after accounting for the increased number of gates.

Figure 2: Diversity of states.
figure 2

a–d, Examples of the density matrices created by applying four of the randomly chosen unitary transformations to simple product states. The bar heights and colours show the absolute value of the output density matrices, with the experimental data shown solid and the theory shown semi-transparent. States a–d have fidelities f=81%,80%,75% and 80%, relative to the ideal states. The Supplementary Information gives the input states and operations used in these examples.

Full size image
Figure 3: Characterization of arbitrary control.
figure 3

a, Histogram of the output-state fidelities f for 160 arbitrary unitary operations applied to one of 16 input product states. b,c, The mean output-state fidelities 〈f〉 for each input state, plotted showing the standard error of the mean (b) and binned into a histogram (c). d, The mean-state fidelities for the 11 operations reconstructed using quantum process tomography. The curves are normal distributions with the same respective mean and standard deviation as the data. The narrower distributions in histograms c,d are expected because they are distributions of means.

Full size image

As a further check on input-state independence, we conduct quantum process tomography8,9 on 11 of the operations. Process tomography reconstructs the completely positive linear map that describes the qubit evolution from initial to final density matrices, . The map includes the possibility of experimental imperfections such as coupling to the environment, which leads to non-unitary evolution. We represent the map by a 16×16 matrix8 . For each of the 11 operations, we determine an experimental process matrix Eexp and compare it to the ideal case by calculating both the entanglement fidelity26 F≡Tr(EidealEexp)/16 and the mean-state fidelity obtained by averaging the output-state fidelities from numerically applying Eexp and Eideal to an unbiased set of 36 input states (formed from the eigenstates of tensor products of the Pauli matrices). These fidelities are related by , where d is the Hilbert-space dimension26 (here d=4). The 11 processes have mean fidelities of 〈F〉=73(3)% and .

We have demonstrated a programmable quantum processor capable of implementing all possible unitary operations on two qubits. To address large-scale problems, many more qubits and gates will be required. In anticipation of such applications, this implementation used only scalable techniques9 such as long-lived qubit storage, quantum information transport and sympathetic cooling. When implementing a larger system, the compound errors from successive operations will need to be reduced by means of error correction27. This will require much higher gate fidelities than shown here, both to achieve fault tolerance and to reduce error correction’s computational overhead28. Nevertheless, the type of device described here could form a processing unit in a larger system7 with programmable registers connected by multidimensional trap arrays19,29 or photonic networks30.

Methods

Algorithmic details.

For a given two-qubit operation U, calculating the 15 single-qubit-gate parameters used in the circuit of Fig. 1b is facilitated by working in the so-called magic basis10,31 given in the main text. Transforming to the magic basis from the two-qubit computational basis |11〉, |10〉, |01〉, |00〉 is accomplished by use of the unitary matrix

The properties of the magic basis rely on unit matrix determinants; thus, we first strip U of any global phase by dividing it by a fourth-root of its determinant, making it a member of SU(4). Global phases exactly vanish in any observable quantity, allowing this modification. In what follows, matrices in the computational basis are denoted with capital letters, and those in the magic basis by lower-case letters; for example, m=Λ†M Λ.

We first find the three degrees of freedom α,β and δ that produce the correct local equivalence class. We decompose the circuit in Fig. 1b as

where V determines the local equivalence class and can be generated using the gate operations shown in Fig. 1b within the dashed rectangle. To construct V, we transform both V and U into the magic basis as v and u and choose α, β and δ such that the eigenvalues of v vT match those of u uT. (We include a global phase e−iπ/4 in V to make it an element of SU(4).) This is done by comparing the analytical form of the eigenvalues of v vT to those of u uT. As u uT is unitary, it has complex eigenvalues of modulus one: λj=eiφj (j∈{1,2,3,4}). We find that α, β and δ are given by the means of pairs of eigenvalue phases. One possibility is α=(φ1+φ2)/2, β=(φ1+φ3)/2 and δ=(φ2+φ3)/2. As no ordering of the eigenvalues is required, there are many such combinations that produce members of U’s local equivalence class. The proof of this assignment is by explicit calculation of the eigenvalues of v vT and is analogous to that given in ref. 14 for the controlled-NOT gate rather than our phase gate.

Second, we find the four single-qubit rotations A, B, C and D that comprise the remaining 12 degrees of freedom. Note that v vT and u uT are unitary symmetric matrices and therefore have real, orthonormal eigenvectors10,16. As they share eigenvalues, it is possible to simultaneously diagonalize them with matrices k and l such that

Here, k and l are eigenvector matrices in which the columns have been permuted such that equation (2) is valid. They are both members of SO(4) (if necessary, one of the eigenvectors can be negated to change the matrix determinant from −1 to 1). By rearranging equation (2), we obtain

(I is the identity matrix), from which we define m≡v†kTl u, also in SO(4). We thus have that

where lTk and m are both real and in SO(4). As they are real orthogonal matrices in the magic basis, they represent single-qubit rotations. We transform equation (3) into the computational basis and compare it to equation (1) to find

To finish, we split and into A, B, C, D ∈ SU(2) and solve for θ,φ and φz for each.