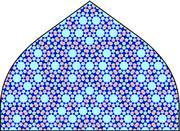
 The pattern on the Darb-i Imam shrine, built in 1453, is almost identical to Penrose tilings, discovered in 1973. Click here for a larger imageK. Dudley and M. Elliff
The pattern on the Darb-i Imam shrine, built in 1453, is almost identical to Penrose tilings, discovered in 1973. Click here for a larger imageK. Dudley and M. ElliffThe complex geometrical designs used centuries ago in Islamic art and architecture were planned with a tiling system that was not discovered in the West until five centuries later, two physicists have claimed.
Islamic tiling patterns were put together not with a compass and ruler, as previously assumed, but by tessellating a small number of different tiles with complex shapes, say Peter J. Lu of Harvard University in Cambridge, Massachusetts and Paul Steinhardt of Princeton University in New Jersey.
The researchers think that this technique was developed around the start of the thirteenth century. By the fifteenth century, it was sophisticated enough to make complex patterns now described as quasi-periodic.
These patterns were 'discovered' in 1973 by the British mathematical physicist Roger Penrose. In 1984, they were found in metal alloys called quasi-crystals that seemed to break the geometric rules of atomic packing.
Perplexing patterns
The patterns in question are called girih. They consist of polygon and star shapes interlaced with zigzag lines.
Writing in this week's Science1, Lu and Steinhardt propose that girih were produced from permutations of a handful of shapes ranging from pentagons to bow-ties. These tiles could be drawn with techniques that were known to medieval Islamic mathematicians.
 Reconstruction of the tiling on the Darb-i Imam shrine.Click here for a larger imagePeter J. Lu
Reconstruction of the tiling on the Darb-i Imam shrine.Click here for a larger imagePeter J. LuScrolls by Islamic artists to explain their methods show tiles with these shapes, confirming that they were used as conceptual building blocks. Lu has found no evidence that the tiles were actually made. "But we speculate they were," he says, "so as to be used as templates in laying out the actual tiling on the side of a building."
"Once you have the tiles, you can make complicated patterns, even quasi-crystalline ones, by following a few simple rules," he adds.
Quasicrystals seem to show five-, ten-, and twelve-fold symmetries, in which they can be superimposed on themselves by rotating them by a fifth, tenth or twelfth of a full circle.
But this would violate the rules of geometry. Polygons with five, ten and twelve sides cannot be packed together without leaving gaps — unlike, say, the hexagons in a honeycomb. Steinhardt solved the problem by showing that Penrose's tiling scheme could generate quasi-crystalline patterns.
ADVERTISEMENT
A girih design on the Darb-i-Imam shrine in Isfahan, Iran, which was made in 1453, is almost identical to a Penrose tiling. One of the pattern's mesmerizing features is that, like a true quasi-crystal, it looks regular but never repeats exactly.
"I'd conjecture that this was quite deliberate", says Lu. "They wanted to extend the pattern without it repeating. Although they were probably unaware of the mathematical properties and consequences of the construction rule they devised, they did end up with something that would lead to what we understand today to be a quasi-crystal."
Visit our tilesreveal_sophistic.html">newsblog to read and post comments about this story.
