Since September 2013 Nature Methods has been publishing a monthly column on statistics called "Points of Significance." This column is intended to provide reseachers in biology with a basic introduction to core statistical concepts and methods, including experimental design. Although targeted at biologists, the articles are useful guides for researchers in other disciplines as well. A continuously updated list of these articles is provided below.
 Importance of being uncertain - How samples are used to estimate population statistics and what this means in terms of uncertainty.
Importance of being uncertain - How samples are used to estimate population statistics and what this means in terms of uncertainty.
 Error Bars - The use of error bars to represent uncertainty and advice on how to interpret them.
Error Bars - The use of error bars to represent uncertainty and advice on how to interpret them.
 Significance, P values and t-tests - Introduction to the concept of statistical significance and the one-sample t-test.
Significance, P values and t-tests - Introduction to the concept of statistical significance and the one-sample t-test.
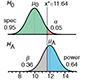 Power and sample size - Use of statistical power to optimize study design and sample numbers.
Power and sample size - Use of statistical power to optimize study design and sample numbers.
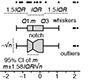 Visualizing samples with box plots - Introduction to box plots and their use to illustrate the spread and differences of samples. See also: Kick the bar chart habit and BoxPlotR: a web tool for generation of box plots
Visualizing samples with box plots - Introduction to box plots and their use to illustrate the spread and differences of samples. See also: Kick the bar chart habit and BoxPlotR: a web tool for generation of box plots
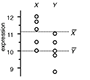 Comparing samples—part I - How to use the two-sample t-test to compare either uncorrelated or correlated samples.
Comparing samples—part I - How to use the two-sample t-test to compare either uncorrelated or correlated samples.
 Comparing samples—part II - Adjustment and reinterpretation of P values when large numbers of tests are performed.
Comparing samples—part II - Adjustment and reinterpretation of P values when large numbers of tests are performed.
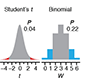 Nonparametric tests - Use of nonparametric tests to robustly compare skewed or ranked data.
Nonparametric tests - Use of nonparametric tests to robustly compare skewed or ranked data.
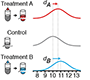 Designing comparative experiments - The first of a series of columns that tackle experimental design shows how a paired design achieves sensitivity and specificity requirements despite biological and technical variability.
Designing comparative experiments - The first of a series of columns that tackle experimental design shows how a paired design achieves sensitivity and specificity requirements despite biological and technical variability.
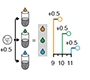 Analysis of variance and blocking - Introduction to ANOVA and the importance of blocking in good experimental design to mitigate experimental error and the impact of factors not under study.
Analysis of variance and blocking - Introduction to ANOVA and the importance of blocking in good experimental design to mitigate experimental error and the impact of factors not under study.
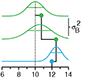 Replication - Technical replication reveals technical variation while biological replication is required for biological inference.
Replication - Technical replication reveals technical variation while biological replication is required for biological inference.
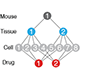 Nested designs - Use the relative noise contribution of each layer in nested experimental designs to optimally allocate experimental resources using ANOVA.
Nested designs - Use the relative noise contribution of each layer in nested experimental designs to optimally allocate experimental resources using ANOVA.
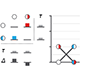 Two-factor designs - It is common in biological systems for multiple experimental factors to produce interacting effects on a system. A study design that allows these interactions can increase sensitivity.
Two-factor designs - It is common in biological systems for multiple experimental factors to produce interacting effects on a system. A study design that allows these interactions can increase sensitivity.
 Sources of variation - To generalize experimental conclusions to a population, it is critical to sample its variation while using experimental control, randomization, blocking and replication for replicable and meaningful results.
Sources of variation - To generalize experimental conclusions to a population, it is critical to sample its variation while using experimental control, randomization, blocking and replication for replicable and meaningful results.
 Split plot design - When some experimental factors are harder to vary than others, a split plot design can be efficient for exploring the main (average) effects and interactions of the factors.
Split plot design - When some experimental factors are harder to vary than others, a split plot design can be efficient for exploring the main (average) effects and interactions of the factors.
 Bayes’ theorem - Use Bayes’ theorem to combine prior knowledge with observations of a system and make predictions about it.
Bayes’ theorem - Use Bayes’ theorem to combine prior knowledge with observations of a system and make predictions about it.
 Bayesian statistics - Unlike classical frequentist statistics, Bayesian statistics allows direct inference of the probability that a model is correct and it provides the ability to update this probability as new data is collected.
Bayesian statistics - Unlike classical frequentist statistics, Bayesian statistics allows direct inference of the probability that a model is correct and it provides the ability to update this probability as new data is collected.
 Sampling distributions and the bootstrap - Use the bootstrap method to simulate new samples and assess the precision and bias of sample estimates.
Sampling distributions and the bootstrap - Use the bootstrap method to simulate new samples and assess the precision and bias of sample estimates.
 Bayesian networks - Model interactions between causes and effects in large networks of causal influences using Bayesian networks, which combine network analysis with Bayesian statistics.
Bayesian networks - Model interactions between causes and effects in large networks of causal influences using Bayesian networks, which combine network analysis with Bayesian statistics.
 Association, correlation and causation - Pairwise dependencies can be characterized using correlation but be aware that correlation only implies association, not causation. Conversely, causation implies association, not correlation.
Association, correlation and causation - Pairwise dependencies can be characterized using correlation but be aware that correlation only implies association, not causation. Conversely, causation implies association, not correlation.
 Simple linear regression - Given data on the relationship between two variables, linear regression is a simple and surprisingly robust method to predict unknown values.
Simple linear regression - Given data on the relationship between two variables, linear regression is a simple and surprisingly robust method to predict unknown values.
 Multiple linear regression - When multiple variables are associated with a response, the interpretation of a prediction equation is seldom simple.
Multiple linear regression - When multiple variables are associated with a response, the interpretation of a prediction equation is seldom simple.
 Analyzing outliers: influential or nuisance - Some outliers influence the regression fit more than others.
Analyzing outliers: influential or nuisance - Some outliers influence the regression fit more than others.
 Regression diagnostics - Residual plots can be used to validate assumptions about the regression model.
Regression diagnostics - Residual plots can be used to validate assumptions about the regression model.
 Logistic regression - Regression can be used on categorical responses to estimate probabilities and to classify.
Logistic regression - Regression can be used on categorical responses to estimate probabilities and to classify.
 Classification evaluation - It is important to understand both what a classification metric expresses and what it hides.
Classification evaluation - It is important to understand both what a classification metric expresses and what it hides.
 Model selection and overfitting - "With four parameters I can fit an elephant and with five I can make him wiggle his trunk". John von Neumann
Model selection and overfitting - "With four parameters I can fit an elephant and with five I can make him wiggle his trunk". John von Neumann
 Regularization - Constraining the magnitude of parameters of a model can control its complexity.
Regularization - Constraining the magnitude of parameters of a model can control its complexity.
 P values and the search for significance - Little P value What are you tryign to say Of significance - Steve Ziliak
P values and the search for significance - Little P value What are you tryign to say Of significance - Steve Ziliak
 Interpreting P values - A P value measures a sample's compatability with a hypothesis, not the truth of the hypothesis.
Interpreting P values - A P value measures a sample's compatability with a hypothesis, not the truth of the hypothesis.
 Tabular data - Tabulating the number of objects in categories of interest dates back to the earliest records of commerce and population censuses.
Tabular data - Tabulating the number of objects in categories of interest dates back to the earliest records of commerce and population censuses.
 Clustering - Clustering finds patterns in data, whether they are there or not.
Clustering - Clustering finds patterns in data, whether they are there or not.
 Principal component analysis - PCA helps you interpret your data, but it will not always find the important patterns.
Principal component analysis - PCA helps you interpret your data, but it will not always find the important patterns.
 Classification and regression trees - Decision trees are a simple but powerful prediction method.
Classification and regression trees - Decision trees are a simple but powerful prediction method.
 Ensemble methods: bagging and random forests - Many heads are better than one.
Ensemble methods: bagging and random forests - Many heads are better than one.
 Machine learning: a primer - Machine learning extracts patterns from data without explicit instructions.
Machine learning: a primer - Machine learning extracts patterns from data without explicit instructions.
 Machine learning: supervised methods - Supervised learning algorithms extract general principles from observed examples guided by a specific prediction objective.
Machine learning: supervised methods - Supervised learning algorithms extract general principles from observed examples guided by a specific prediction objective.
 Statistics versus machine learning - Statistics draws population inferences from a sample, and machine learning finds generalizable predictive patterns.
Statistics versus machine learning - Statistics draws population inferences from a sample, and machine learning finds generalizable predictive patterns.
 The curse(s) of dimensionality - There is such a thing as too much of a good thing.
The curse(s) of dimensionality - There is such a thing as too much of a good thing.
 Optimal experimental design - Customize the experiment for the setting instead of adjusting the setting to fit a classical design.
Optimal experimental design - Customize the experiment for the setting instead of adjusting the setting to fit a classical design.
 Predicting with confidence and tolerance – For studying phenomena that are ‘typical’ rather than ‘average’.
Predicting with confidence and tolerance – For studying phenomena that are ‘typical’ rather than ‘average’.
 Two-level factorial experiments – Getting the benefits of probing multiple experimental factors at a time.
Two-level factorial experiments – Getting the benefits of probing multiple experimental factors at a time.
