Abstract
In the clinical application of genomic data analysis and modeling, a number of factors contribute to the performance of disease classification and clinical outcome prediction. This study focuses on the k-nearest neighbor (KNN) modeling strategy and its clinical use. Although KNN is simple and clinically appealing, large performance variations were found among experienced data analysis teams in the MicroArray Quality Control Phase II (MAQC-II) project. For clinical end points and controls from breast cancer, neuroblastoma and multiple myeloma, we systematically generated 463 320 KNN models by varying feature ranking method, number of features, distance metric, number of neighbors, vote weighting and decision threshold. We identified factors that contribute to the MAQC-II project performance variation, and validated a KNN data analysis protocol using a newly generated clinical data set with 478 neuroblastoma patients. We interpreted the biological and practical significance of the derived KNN models, and compared their performance with existing clinical factors.
Similar content being viewed by others
Introduction
The US Food and Drug Administration MicroArray Quality Control (MAQC) project is a community-wide effort to analyze the technical performance and practical use of emerging biomarker technologies (such as DNA microarrays, genome-wide association studies and next generation sequencing) for clinical application and risk/safety assessment. A major objective of the second phase of the project (MAQC-II) is to evaluate the performance of microarray-based classifiers for clinical use.1 To facilitate this investigation, the MAQC-II project obtained three large clinical data sets containing approximately 700 samples. These data profile three types of cancers (breast cancer, neuroblastoma and multiple myeloma) generated by the Affymetrix or Agilent microarray technologies. The MAQC-II organized these samples into six clinical end points, two positive controls and two negative controls (Table 1).
The MAQC-II project extensively evaluated common practices for classifier development and validation, such as dealing with an exceedingly large feature space (that is, ‘curse of dimensionality’), selecting the best performing model among those developed (that is, multiple comparisons problem) and estimating the performance of the classifiers for future prediction (that is, cross-validation (CV) versus external validation (EV)). An unbiased way to determine best practices for classifier development and validation is to systematically explore the entire parameter space of various classification algorithms. However, due to the overwhelming number of modeling parameters that contribute to the classifier performance, the MAQC-II consortium determined that it was not administratively feasible to conduct such a study. Consequently, 36 MAQC-II analysis teams from academia, industry and the Food and Drug Administration selected their own methods and parameter spaces to build classifiers using the same labeled data sets and then submitted them to MAQC-II. Among the 19 779 classification models submitted by 36 teams, 9742 were k-nearest neighbor-based (KNN-based) models (that is, 49.3% of the total).
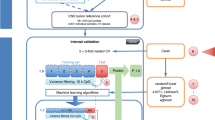
Analyzing these KNN classifiers, we made two key observations: first, KNN models have generally performed well compared with more complicated models—a finding which is also in line with previous studies.5, 6 Second, there have been large variations in prediction performance among KNN models submitted by different teams (Supplementary Figure S1). Thus, the main goals of this study were (1) to motivate the use of classifiers such as KNN that capture nonlinear interactions between features as apposed to main effects; (2) to investigate the modeling factors that contribute to the variations in KNN classifier performance; (3) to develop a robust KNN data analysis protocol (kDAP) that can provide reliable KNN models for clinical use; (4) to show how this kDAP can be applied to a newly generated clinical data set and (5) to validate the KNN predictor results through both biological interpretation and comparison with practical clinical risk factors. As shown in Figure 1, we develop the kDAP using MAQC-II data and assess its clinical use by comparing its performance to existing clinical factors for risk stratification.
Neuroblastoma case study to show clinical applications of KNN classifier. We designed a method to test whether KNN produces classifiers of good clinical relevance. First, we developed our approach using MAQC-II gene expression data. Then, we applied this approach to additional Neuroblastoma data and compared it to existing clinical factors for risk.
Background
Besides being popular in the MAQC-II Project, KNN is also a common method used for classification in the literature such as Nature series journals,7, 8 Proceedings of the National Academy of Sciences9, 10, 11 and the New England Journal of Medicine.12, 13 The KNN classifier assigns a label to a new unknown sample by considering the labels of the k most similar examples in a training set.14, 15 When distinguishing between two classes, the fraction of votes from one class must exceed a threshold to classify the new sample to that class. Parameters embedded in this model include the similarity measure or distance metric, number of neighbors (k), decision threshold and how to assign weights to each vote. In clinical studies, if global trends exist in gene expression, a linear classifier such as logistic regression can classify a new sample using a weighted combination of expression values.16, 17 If nonlinear relationships exist, KNN is a better choice because it has the capacity to learn nonlinear relationships between genes. Within the MAQC-II project, we investigate the factors of KNN that contribute to performance variations and also compare its performance to logistic regression.
In the past, published studies seldom describe in detail the methods used to select KNN parameters. Even in the studies that consider several parameters, the parameter space is often limited. For example, Rosenfeld et al.8 have used a KNN classifier to predict cancer tissue origin from microRNA profiles. They have determined that the optimal k parameter was 3, but only considered a limited space that includes k values of 1, 3 and 5. Lu et al.7 have considered a similar KNN parameter space to classify cancer using microRNA profiles. Hoshida et al.12 have used a KNN classifier (among other classifiers) and have considered a KNN parameter space of k=1, 3, 5 and 7 to predict hepatocellular carcinoma treatment outcome from gene expression data. Indeed many studies use KNN for prediction of various clinical properties including breast cancer patient survival,9 identification of neuroblastoma differentiation markers,10 hepatitis treatment outcome11 and early detection of prostate cancer.13 Given the lack of a comprehensive examination of KNN's effectiveness when applied to gene expression studies, it is difficult to draw conclusions on what have caused the large variations in the 9742 MAQC-II KNN models. Thus, we have designed and conducted a meta-analysis of KNN modeling.
To identify factors that cause the performance variations among KNN models, we have surveyed the metadata and data analysis protocols from different teams in the MAQC-II project and reviewed previous KNN modeling data.14, 15 From this survey, we identify six factors that are relevant to KNN modeling: feature ranking method, number of features, distance metric, number of neighbors, vote weighting and decision threshold. Among these, distance metric, number of neighbors, vote weighting and decision threshold were not explicitly shown in the MAQC-II metadata survey, but the number of neighbors was sometimes volunteered. Much like the common practice in medical and science journals, many of the MAQC-II data analysis teams either did not specify these parameters or did not explore the parameter space.
Therefore, we decide to conduct a more thorough study of KNN model performance over a large KNN parameter search space. Specifically, we systematically explore modeling factors to identify those that contribute to performance, particularly predictable performance, of KNN classifiers using the six clinical end points and four control end points from three large MAQC-II cancer data sets. We develop a kDAP with which a reliable and robust KNN classifier is likely to be obtained. Then, we study the predictability of this kDAP on a new data set generated using a different microarray technology to measure the gene expression of a subset of the original neuroblastoma patient samples.
Finally, using neuroblastoma as a case study, we present a clinical use of the kDAP. The success of treating neuroblastoma depends on the accuracy of risk assessment and early detection. Although retrospective analysis of neuroblastoma statistics indicates an overall improvement of treatment success, mortality rates for advanced-stage neuroblastoma are still high.18, 19 The International Neuroblastoma Risk Group has established a set of clinical factors for predicting disease recurrence and survival. These clinical factors include disease stage, age of the patient at diagnosis, histological features and several genetic markers.20 However, it is believed that gene-expression-based methods could further refine risk stratification.21 Indeed, several studies have identified and proposed panels of genomic markers to predict event-free survival (that is, survival without recurrence or metastasis within a specific period of time after diagnosis or treatment).4, 22, 23 Here, we assess the clinical use of our kDAP by comparing its prediction performance to each clinical factor for event-free survival of neuroblastoma patients.
Materials and Methods
Three cancer data sets and ten end points
The detailed description of each data set and associated end points is available from the MAQC-II main paper.1 We briefly summarize the three cancer data sets in Table 1. Each cancer data set contains two clinical end points. For both neuroblastoma and multiple myeloma, positive and negative controls are included. These two types of controls are necessary to assess the performance of the clinically relevant end points against the theoretical maximum and minimum performance provided by the controls. An independent working group under the MAQC-II divided each data set into the training and validation sets using a time-stratified approach. The date change represents a realistic scenario for clinical applications where the data for new patients are generated at later dates than the original training set.1 This potentially introduces batch effects and other variations that are largely unpredictable, including adoption of new microarray chip designs based on manufacturer design improvements.17, 18, 19 We conduct CV for each model on the training set, followed by EV on the validation set.
In addition to the three data sets shown in Table 1, the MAQC-II also has an independent neuroblastoma data set using a different microarray technology (customized one-color array). It covers 478 neuroblastoma patients at a much later date than both the training and validation data. This data set provides an important validation platform to test our proposed kDAP, and to evaluate the prediction power of the resulting KNN models. The KNN models have shown robustness to change in microarray technology including many overlapping probes.24
Performance metrics
All conclusions pertaining to the performance of a classifier depend on the choice of a performance metric. Different performance metrics may lead to different conclusions for selecting the best predictive model,25 and some metrics have yet to be subjected to a thorough empirical and theoretical analysis.26 Technology and population changes (for example, batch effect and class prevalence) increase the variance of threshold-based metrics.27 These factors do not appear in CV because the training and test data are homogeneously mixed. However, in clinical applications, these factors are likely to change. For this study, we included a threshold-free metric based on the ‘area under the receiver operating characteristic curve’ (AUC), and a threshold-based metric, Matthews correlation coefficient (MCC).25 AUC aggregates performance across all thresholds, and thus favors models that perform well for a variety of thresholds. MCC evaluates a model based on its predicted class labels, and thus favors models that perform well at a particular threshold.
A model that performs well on AUC and poorly on MCC indicates that there is a change in data set properties (for example, class prevalence), which in turn affects threshold in KNN classification. A model that performs well on MCC and poorly on AUC indicates that there is an overall data set shift, such as a batch effect, for which a ‘lucky’ threshold still performs well. To select KNN models that perform well for a variety of thresholds and also tune threshold during CV we incorporate both metrics to create a unified performance metric in the kDAP. We scale MCC to fall in the same range as AUC and then take the average (that is, 0.5 × AUC+0.25 × (MCC+1)). Then, to assess whether models perform predictably well on EV we use the minimum of CV and EV performance (that is, Min(CV,EV)).
Comparison of KNN to logistic regression on Food and Drug Administration data sets
We compared KNN to logistic regression using the labeled training sets in the MAQC-II project. For each of the 10 end points, we performed 15 iterations of fivefold CV. Within each fold, we selected parameters for KNN and logistic regression using a nested threefold CV. That is, we use four-fifths of the training set to select the top performing parameters from nested CV, and then evaluate the selected parameters on the remaining one-fifth of the training set. Each iteration results in a single estimate of performance using AUC and MCC. For both classifiers, we vary feature ranking method, number of features and threshold. For KNN, we also vary the number of neighbors.
Systematic examination of KNN modeling factors
We constructed a general workflow with varying parameters for feature ranking, number of features, distance metric, number of neighbors, vote weighting and decision threshold (see Figure 2) as the following:
-
feature ranking methods (three total):
-
significance analysis of microarrays d-score (SAM d-value)
-
fold change (FC) ranking with P-value threshold of 0.05 (FC&(P<0.05)), and
-
P-value ranking with FC threshold of 1.5 (P&(FC>1.5));
-
-
numbers of features (26 total):
-
N between 5 and 125 in steps of five; and using all features;
-
-
distance metrics (three total):
-
Euclidean distance,
-
cosine distance, and
-
city block distance;
-
-
numbers of neighbors (30 total):
-
k between 1 and 30;
-
-
vote weighting (two total):
-
equal weighted voting and
-
distance weighted voting; and
-
-
decision thresholds (33 total):
-
θ between 0.01 and 0.99.
-
Generalized workflow for the systematic KNN analysis. The factors shown in black were found to have very little contribution to performance variance. Representative values of each factor in the column indicate that the complete analysis of all factors (varying only one factor for each model) allows for accurate separation of the influence of each factor (for the purposes of ANOVA analysis).
Feature ranking methods order genes according to their individual ability to distinguish between the two classes of patients. The number of features specifies how many of the top performing genes are selected for inclusion in the classifier. We excluded more sophisticated gene selection algorithms such as sequential or search-based feature selection because they were computationally impractical for this combinatorial study. The number of neighbors specifies how many similar samples cast a vote for the label of the new sample. Vote weighting assigns different importance to each vote, whereas decision threshold specifies what fraction of votes for the positive class is required to classify the new patient as positive.
We conducted an eight-way analysis of variance (ANOVA) using a random effects linear model to assess the relative contribution of each modeling factor to the performance variations. In addition to the six modeling factors, we included a factor for data set, and within data set, we included a nested subfactor for end point. For example, class prevalence and labeling errors contribute to end point variation, whereas sample size and batch effect contribute to data set variation. As with all regression analyses, confounding variables may result in misleading conclusions. For example, the average difficulty of the end points may vary between data sets and this variation would be attributed to the data set factor, when in fact it belongs to end point. Because end point is nested within data set, the sum of their variance could be interpreted as a single ‘end point’ factor combining the effects of data set and end point.
Results
First, we compared KNN to logistic regression to justify the use of nonlinear classifiers for gene expression and to carry out a deeper investigation of KNN modeling factors. Then, we performed a systematic combinatorial study by varying the intrinsic KNN modeling parameters to generate 463 320 classifiers for each of the 10 end points from three clinical cancer data sets (including 4 control end points). On the basis of these classifiers, we first analyzed the impacts of each modeling factor on the classifier performance. Next, we took these results to generate a kDAP as guidance for developing a predictive classifier for clinical applications. Finally, we evaluated the kDAP by a newly generated large cancer data set for neuroblastoma.
Comparing KNN to logistic regression
Table 2 provides mean performance and the P-value of a paired t-test for each end point to determine if KNN and logistic regression perform significantly differently. Using a Bonferroni adjusted significance level of 0.005, we found that KNN performs equally well or significantly better than logistic regression on all clinical end points. Specifically, KNN performs significantly better on pathological complete response of breast cancer and overall survival of neuroblastoma, as well as event-free survival of multiple myeloma using MCC performance metric. Logistic regression, however, only performs significantly better when classifying gender (positive control) for the multiple myeloma data set.
To illustrate the specific advantage of KNN for the breast cancer data set, we selected two genes from among the 1010 unique genes, which were collected as the top 20 by any of the ranking methods used on any of the 225-folds of nested CV. Figure 3 shows the breast cancer samples labeled by pathological complete response, and divides the feature space according to logistic regression and KNN decision boundaries. Whereas linear classifiers, such as logistic regression, divide the feature space using a straight line, nonlinear classifiers such as KNN have the flexibility to create more complex decision surfaces. Figure 3a shows such a surface using genes that appeared in 28% of the nested folds. KNN correctly classifies the positive samples that wrap around a central and lower-right negative region. We also implemented a search across all gene pairs to identify relatively better performing pairs and found similar relationships. Figure 3b provides another example of this ‘ball-in-socket’ structure (this time with switched labels). If these complex interactions are relevant for classification, only nonlinear classifiers like KNN can model them.
Feature space comparison of a linear and nonlinear classifier on (a) genes that perform well individually and (b) genes that only perform well together. The straight line that separates the white+blue region from the white+yellow region represents the logistic regression decision boundary. KNN provides a curved decision boundary that disagrees with logistic regression in the blue and yellow regions.
Systematic analysis of modeling factors
Table 3 summarizes the variance explained by ANOVA for CV and EV. Because models have to perform well on both to show good predictability, we used the Min(CV,EV) to assess the KNN models. The factor of end point is consistently the major source of variation for classifier performance, which is consistent with the MAQC-II project results explained in the main article.1 In addition, we have shown that the factor of data set captures the second most variance, which may indicate the impact of the underlying characteristics such as sample size or batch effect. Most of the remaining variance can be explained by decision threshold, number of neighbors, feature ranking method and number of features. Perhaps unexpectedly feature ranking contributes less to the overall variance. This suggests that the three feature ranking methods perform similarly well for KNN, and it does not mean that feature ranking itself is less important. Decision threshold comprises a large portion of the MCC variance, which is consistent with the fact that threshold must be tuned to achieve good performance. While it is important to avoid the potential misinterpretation that factors with large variation caused that variation, some factors appear not to contribute. For example, as expected, decision threshold makes no contribution to AUC variance. However, different distance metrics and vote weightings performed nearly identically. Thus, we selected the conventional Euclidean distance and equal-weighted voting for all further analysis.
We also conducted a full two-way interaction ANOVA model on a reduced parameter space (because of memory restrictions) and found results consistent with Table 3. The primary contributing interactions include end point as a factor in addition to a large contribution from the decision threshold when using MCC. The choice of k defines equivalent ranges of threshold based on the k+1 possible voting outcomes. Clearly, the choice of k influences the choice of threshold as can be seen in Supplementary Figure S2.
The number of neighbors (k) affects predictable performance significantly. Box plots in Figure 4 illustrate the effect of k on the minimum AUC of EV and CV (predictable performance). Research articles often report ad hoc selection of k between one and seven without justification.8, 28, 29, 30 Our study suggests that larger k often improves overall performance of a classifier as well as its predictable performance. As depicted in Figure 4, higher mean performance and lower variance can be attained at larger values of k. However, the optimal value of k remains end point specific.
Number of neighbors affects cross-validation performance for end points D, E, F, G, J, and K in subparts (a), (b), (c), (d), (e), and (f), respectively. Box plots represent the distribution of predictable performance (i.e., Min(CV,EV)) for the population of models with varying k using AUC. For each box plot, a white circle indicates the median; the black box joins the 25th and 75th percentiles and black dots indicate outliers. High medians with small range are desirable.
Figure 5 shows the parameter space including feature ranking method, number of features and number of neighbors using AUC. In general, cross-validation predicts a slightly better performance than observed in external validation (that is, EV-CV is less than zero). This is consistent with our general understanding that CV tends to overestimate the EV performance. For both positive controls (end points H and L), EV-CV is nearly zero with a homogeneous distribution. There seems to be high concordance between CV and EV for an ‘easy’ end point regardless of the choice of feature ranking method, and the number of features and neighbors. However, EV-CV for both negative controls (end points I and M) is rather heterogeneous. This indicates that selecting a robust set of parameters in CV is important for achieving a reliable estimation for the EV performance.
No single set of parameters perform reproducibly for all end points. The reproducibility of model performance is quantitatively measured as the percent change of external validation (EV) from internal cross validation (CV). Across the KNN parameter space (including k, feature ranking method and number of features with a decision threshold of 0.5), the difference between EV and CV AUC ranges from +20 to −20%, with distinct regions of higher or lower EV performance relative to CV. Reproducible models are the white regions of the heat map, indicating very small differences between EV and CV. Overall, no single set of KNN parameters performs well for all end points.
In most published studies using KNN, the default decision threshold of 0.5 is commonly used in binary classification. As shown in Supplementary Figure S2, the optimal decision threshold varies with the end points studied. Whether selecting a decision threshold a priori or guided by CV, the tradeoffs are not well understood. We compared both scenarios in terms of root mean-squared difference of performance MCC between CV and external validation. As shown in Table 4, no significant difference between the two scenarios is observed across all clinical end points. For both positive and negative controls, it is almost identical to use 0.5, or to use CV in deciding decision threshold. This indicates that there is little threshold dependency for either signal dominant (positive control) or noise dominant (negative control) data sets.
KNN data analysis protocol
On the basis of the systematic analysis of modeling factors detailed above, we propose a kDAP, which can be used in surveying a large parameter space to select a candidate model (Supplementary Table S1). Briefly, we suggest to use a fivefold CV over an extensive feature space (N=5–200 in steps of five), to use three feature ranking methods (significance analysis of microarrays, fold-change ranking with P-value <0.05, and P-value ranking with fold-change greater than 1.5) and to try a large range of neighbors (k from 1 to 30). In general, we suggest selecting the top performing model on CV for future sample prediction. Regarding performance metric, we combine AUC and MCC (that is, 0.5 × AUC+0.25 × (MCC+1)) to select the candidate models. To evaluate a model's predictability and performance on EV, we use Min(CV,EV).
In the MAQC-II project, 36 participating analysis teams developed a large number of classifiers for each end point based on the training data. However, each team only nominated one classifier per end point for blind testing on the validation set, resulting in 251 classifiers for the 10 clinical end points. These so-called candidate models were developed using various machine learning methods and provide a fair representation of the common practice in the microarray gene expression analysis community. Figure 6 compares the kDAP-derived models with the candidate models from MAQC-II. The kDAP classifiers perform among the better candidate models including the KNN-based models. In addition, the kDAP classifiers are close to the diagonal line indicating predictable EV performance. Supplementary Figure S3 shows a kernel-smoothed density of the scatter plots in Figure 6 in terms of EV–CV, where values near zero are desirable. The kDAP classifiers appear in a region near the middle of this distribution.
KNN data analysis protocol compared to MAQC-II candidate models for end points D, E, F, G, J, and K in subparts (a), (b), (c), (d), (e), and (f), respectively. Scatter plots show external validation versus cross-validation performance for the proposed kDAP model (triangle), other MAQC-II candidate KNN models (square) and other (non-KNN) MAQC-II candidate models (circle).
Clinical use of kDAP
Using neuroblastoma clinical end points as a case study, we illustrate the clinical use of the kDAP by exploring a large parameter space. We consider the biological and practical interpretation of the derived modeling parameters, the predictive performance of the derived models compared to existing clinical factors, and the biological interpretability of the derived gene lists.
There are two sets of data generated using neuroblastoma patient samples. The original MAQC-II neuroblastoma data set was generated using a two-color Agilent microarray platform as shown in Table 1. Then at a much later date, a new data set was generated using a one-color Agilent microarray platform.24 The new data set contains 21 fewer samples, approximately 700 fewer genes and covers the same end points. To mimic the real clinical application, we kept the identity of these end points and labels in the validation set confidential during our entire KNN classification model selection process (that is, we were not aware of which two of the four end points were controls, nor the identities of any of the samples).
KNN model parameters selected by kDAP
First, we apply the kDAP to develop KNN classification models by using the MAQC-II-provided training sets of 236, 237, 244 and 244 patients. Second, we use the top performing CV KNN model for each end point to predict class labels of the subsequently released validation set of 159, 175, 219 and 234 patients. Table 5 summarizes both the CV and EV performances. All four end points show strong correspondence between model parameters and performance for the one-color (new) and two-color (original) data set.
In general, we expect the number of features (N) to indicate the complexity of the biological process (that is, more genes are required to model relationships that are more complex). The performance of models with a specific number of neighbors (k) may also be related to complexity of the classification problem. Difficult problems may require more training data points to reduce the effect of outliers, or may lead to over-fitting. Simple problems may lead to an arbitrary choice of k as very little training data are required to make the decision. The choice of decision threshold tends toward the prevalence (defined as percentage of negative samples) of the training set, especially for high k. When the candidate model's parameters make sense according to our understanding of the clinical problem, we are more confident in its performance on future data sets.
The positive controls provide an example of simple biological problems resulting in a simple classifier with a small number of difficult or outlier samples. For both positive controls, the peak performing KNN model during CV uses a small number of features, large number of neighbors and low threshold favoring the prevalence, which is consistent with our understanding of parameter behavior (Table 5). A smaller number of features focuses the model on a few quality genes, and large k smoothes, and simplifies the decision surface, yielding a high-performing model for an easy end point. Both negative controls use a small number of neighbors and small enough threshold to yield a complex classifier favoring the larger class and resulting in higher sensitivity and lower specificity. It is important to note that all models perform uniformly poorly on negative controls.
Supplementary Figure S4 shows the overall distribution of the population of models for the clinical end points compared with the control end points. The overall survival and event-free survival end points use large k and moderate N, falling somewhere between the positive and negative controls in difficulty. For both clinical end points, the kDAP performs slightly worse in EV compared with CV, which is also consistent with what we have observed for the MAQC-II data sets using KNN. These models still perform predictably well in terms of Min(CV,EV).
Case study for clinical use of kDAP
In Figure 7, we use Kaplan–Meier plots to compare the performance of the kDAP to some clinical factors.4 Established by the International Neuroblastoma Risk Group, the commonly used factors include patient age at diagnosis, histology, disease stage at diagnosis, MYCN status and chromosomal status.20 Retrospective neuroblastoma statistics have shown that survival rates are significantly associated with age at diagnosis, with younger patients showing more favorable results.19 Also, genetic anomalies. such as MYCN amplification or chromosomal deletions or imbalance, are associated with patient survival.33, 34, 35 In addition, histological information (for example, morphological characteristics and degree of tissue differentiation) were shown to further improve risk stratification.31 All of these factors are included as part of the International Neuroblastoma Staging System, which categorizes neuroblastoma into stages 1, 2, 3, 4s and 4.36 Stages 1, 2 and 4s are generally favorable, with high patient survival rates, compared with stages 3 and 4.
Comparison of KNN prediction of neuroblastoma event-free survival to established clinical factors for risk stratification. Kaplan–Meier plots compare the prognostic accuracy of the kDAP model on (a) two-color data set and (b) one-color data set compared with several clinical factors: (c) age of the patient at diagnosis, (d) stage of the disease at diagnosis, (e) favorable or unfavorable histology using the Shimada system,31 (f) MYCN amplification,32 (g) risk stratification from the German Neuroblastoma Trials (intermediate-risk (IR) patients were grouped with low-risk (LR) patients), (h) the status of chromosome 11q23 and (i) the status of chromosome 1p36.
As shown in Figure 7, for event-free survival of neuroblastoma patients, the KNN predictor performs among the better clinical factors. Using log-rank statistics, we find that the KNN predictor has the smallest P-value. In addition, the kDAP optimizes for the 900-day cutoff for event-free survival and outperforms the clinical factors at this cutoff (higher green line and lower red line at the vertical dashed line at 900 days).
MYCN amplification, measured using fluorescent in situ hybridization, appears to be the best clinical factor for stratifying patients into low- and high-risk groups. In our gene expression data, MYCN is overexpressed nearly twofold (1.9) in high-risk patients. Among the top-ranked genes in the KNN model are several genes known to be related to neuroblastoma (Table 6). For example, Gene Ontology analysis using GOstat reveals that the top 200-ranked genes primarily represent cell-cycle and cell division processes.37 This is not surprising as high-risk neuroblastoma patients typically show faster disease progression or recurrence, hence, faster cell growth. Also, NTRK1, a neuroblastoma tumor suppressor is overexpressed nearly fourfold in low-risk patients.38 In addition, NEK2 and MAPT are oppositely expressed by nearly two-fold.39 Several other genes in Table 6 have been previously implicated in neuroblastoma or cancer, in general, including CNTNAP2,40 EBF1,41 PDE4DIP,42 AMIGO2,43 PKIB,44 EPHA5,45 CENPA,46 CENPF,47 SCG2,48 TWIST149 and BMP7.50
Discussion
Development and assessment of microarray-based classifiers has become an active area of research in pharmacogenomics to improve clinical diagnosis and treatment. In comparison with previous work, our studies have a number of new and advanced features.
First, we used three large cancer data sets each having two clinical end points. The classifiers were developed on training sets and evaluated on validation sets that were generated on different dates to mimic real-world clinical applications. The validation sets are sufficiently large, which provide a robust estimation of the classifier performance. In this study, we centered our analysis to a specific measurement, Min(CV,EV), that evaluates the minimum performance between CV and EV. This measure favors models that perform predictably well and assesses whether the CV-derived classifier is reliable and robust to predict future samples in a clinical application.
Second, we motivated the use of nonlinear classifiers such as KNN for gene expression analysis by showing specific examples where genes show complex relationships relevant to classification. Interestingly, the complex interaction in Figure 3a was identified by relatively unsophisticated feature ranking methods that do not explicitly search for such structure. That is, each gene performs well enough on its own to perform in the top 0.1% of all genes. Sequential or search-based feature selection could identify the pair of genes in Figure 3b and are worthy of future research. We speculate that these feature interactions explain the significant performance improvement of KNN over logistic regression for end point D.
Third, we conducted a combinatorial study by exploring a list of modeling parameters related to KNN classifier development. Realizing that different performance metrics might lead to divergent conclusions, we also included two performance metrics (that is, AUC and MCC) to assess the classifier performance. Our approach is different from many published studies that validate novel algorithms for clinical applications in that they use fixed modeling parameters, a single performance metric, CV without EV or EV using only one selected model. Instead of relying on a single-point estimate of a classifier's validation performance, we acquire an understanding of the sensitivity of the model to perturbations in modeling factors or data set properties and thus gain a comprehensive picture to inform our kDAP.
Fourth, positive and negative controls are available for the multiple myeloma and neuroblastoma data sets. There are several benefits to include both controls in clinical practice. For example, using this information, we are able to compare the performance of the clinically relevant end points against the theoretical maximum and minimum performance provided by the controls. The distributions of clinical end points for patients with multiple myeloma are closer to the negative control than that observed for patients with neuroblastoma, indicating that the multiple myeloma data set is more difficult to model compared with the neuroblastoma data set (Supplementary Figure S4). In addition, both controls can serve as quality metrics to identify overfitting (for example, bias in feature selection) and modeling errors (for example, mistakes in the computer code). As both positive and negative controls are readily available for most clinical data sets, we strongly recommend that they be included as a baseline practice for developing classifiers using gene expression profiles or other emerging molecular biomarker technologies in clinical applications. In addition to outperforming negative controls, the kDAP performs comparably well to currently established clinical factors for neuroblastoma event-free survival. Because the kDAP optimizes for the 900-day cutoff for event-free survival, it better differentiates the samples for that cutoff.
Although no single set of modeling parameters perform equally well for all end points and most factors are end point specific, several important patterns are observed. For example, distance metric and vote weighting are not significant. Factors such as feature ranking method, number of features, number of neighbors and decision threshold interact with each other to affect the classifier performance. In particular, we observe the impact of the decision threshold to the classifier performance as depicted in Supplementary Figure S2. It appears that the choice of threshold depends on the prevalence of the training set and the target population. Although choosing an a priori decision threshold of 0.5 in CV generally provides a fair estimation for EV, the complex nature of decision threshold related to the classifier performance may deserve further investigation.
Summary
Through systematic analysis of the KNN modeling practice using large cancer gene expression microarray data sets with both positive and negative controls, we have developed a KNN data analysis protocol (kDAP) for clinical applications. We have considered six modeling factors for KNN and find that two do not contribute to variations in predictive performance: distance metric and vote weighting. Using the remaining factors (feature ranking method, number of features, number of neighbors and decision threshold), we find that the selection of all remaining parameters to be end point specific. In particular, the kDAP selects much larger values of k than that typically reported in practice, perhaps due to the large size of the MAQC-II data sets by current standards. The kDAP candidate models perform predictably well on the external validation sets compared with other candidate models in the MAQC-II project. More importantly, we use a clinical case study, neuroblastoma cancer data set, to validate the kDAP. The kDAP produces consistent KNN prediction models on a newly generated data set created by a different microarray technology. The resulting KNN model parameters reveal the underlying biological and practical characteristics of the end points. The kDAP also improves on existing clinical factors for risk stratification for predicting the 900-day cutoff of event-free survival and performs comparably for stratifying low- and high-risk patients for event-free survival. In addition, many of the genes used in the candidate model correspond to known genes implicated in neuroblastoma or cancer.
The kDAP provides a starting point for the research community to enhance the best practice for use of KNN classifiers in clinical genomics. Moreover, the described approach should be extendable to other machine learning methods as well as other emerging molecular biomarker technologies in clinical applications. By validating the kDAP against existing clinical factors, we envision its application to emerging problems where no suitable factors exist. Whereas discovering new clinical factors for disease has been a painstaking hypothesis-driven pursuit, we have shown the use of the hypothesis-free kDAP that may increase the translation of clinical predictors.
Abbreviations
- ANOVA:
-
analysis of variance
- AUC:
-
area under the receiver operating characteristic (ROC) curve
- CV:
-
cross-validation
- DAP:
-
data analysis protocol
- EV:
-
external validation
- Min(CV,EV):
-
minimum of cross-validation performance and external validation performance (predictable performance)
- KNN:
-
k-nearest neighbor
- MAQC-II:
-
MicroArray Quality Control consortium phase II (predictive modeling)
- MCC:
-
Matthews correlation coefficient
- SAM:
-
significance analysis of microarrays
References
Shi L . MAQC-II Project: a comprehensive survey of common practices for the development and validation of microarray-based predictive models. Nat Biotechnol 2010; advance online publication, doi:10.1038/nbt.1665.
Gong Y, Yan K, Lin F, Anderson K, Sotiriou C, Andre F et al. Determination of oestrogen-receptor status and ERBB2 status of breast carcinoma: a gene-expression profiling study. Lancet Oncol 2007; 8: 203–211.
Shaughnessy Jr JD, Zhan F, Burington BE, Huang Y, Colla S, Hanamura I et al. A validated gene expression model of high-risk multiple myeloma is defined by deregulated expression of genes mapping to chromosome 1. Blood 2007; 109: 2276–2284.
Oberthuer A, Berthold F, Warnat P, Hero B, Kahlert Y, Spitz R et al. Customized oligonucleotide microarray gene expression-based classification of neuroblastoma patients outperforms current clinical risk stratification. J Clin Oncol 2006; 24: 5070–5078.
Dudoit S, Fridlyand J, Speed TP . Comparison of discrimination methods for the classification of tumors using gene expression data. J Am Stat Assoc 2002; 97: 77–87.
Shedden K, Taylor JM, Enkemann SA, Tsao MS, Yeatman TJ, Gerald WL et al. Gene expression-based survival prediction in lung adenocarcinoma: a multi-site, blinded validation study. Nat Med 2008; 14: 822–827.
Lu J, Getz G, Miska EA, Alvarez-Saavedra E, Lamb J, Peck D et al. MicroRNA expression profiles classify human cancers. Nature 2005; 435: 834–838.
Rosenfeld N, Aharonov R, Meiri E, Rosenwald S, Spector Y, Zepeniuk M et al. MicroRNAs accurately identify cancer tissue origin. Nat Biotechnol 2008; 26: 462–469.
Miller LD, Smeds J, George J, Vega VB, Vergara L, Ploner A et al. An expression signature for p53 status in human breast cancer predicts mutation status, transcriptional effects, and patient survival. Proc Natl Acad Sci USA 2005; 102: 13550–13555.
Hahn CK, Ross KN, Warrington IM, Mazitschek R, Kanegai CM, Wright RD et al. Expression-based screening identifies the combination of histone deacetylase inhibitors and retinoids for neuroblastoma differentiation. Proc Natl Acad Sci USA 2008; 105: 9751–9756.
Sarasin-Filipowicz M, Oakeley EJ, Duong FH, Christen V, Terracciano L, Filipowicz W et al. Interferon signaling and treatment outcome in chronic hepatitis C. Proc Natl Acad Sci USA 2008; 105: 7034–7039.
Hoshida Y, Villanueva A, Kobayashi M, Peix J, Chiang DY, Camargo A et al. Gene expression in fixed tissues and outcome in hepatocellular carcinoma. N Engl J Med 2008; 359: 1995–2004.
Wang X, Yu J, Sreekumar A, Varambally S, Shen R, Giacherio D et al. Autoantibody signatures in prostate cancer. N Engl J Med 2005; 353: 1224–1235.
Bishop CM . Pattern Recognition and Machine Learning. Springer: New York, 2006, 738pp.
Duda RO, Hart PE, Stork DG . Pattern Classification, 2nd edn. Wiley: New York, 2001, 654pp.
DeRisi JL, Iyer VR, Brown PO . Exploring the metabolic and genetic control of gene expression on a genomic scale. Science 1997; 278: 680–686.
Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 1999; 286: 531–537.
Aydn GB, Kutluk MT, Yalcn B, Buyukpamukcu M, Kale G, Varan A et al. Neuroblastoma in Turkish children: experience of a single center. J Pediatr Hematol Oncol 2009; 31: 471–480.
Cotterill SJ, Pearson AD, Pritchard J, Foot AB, Roald B, Kohler JA et al. Clinical prognostic factors in 1277 patients with neuroblastoma: results of the European Neuroblastoma Study Group ‘Survey’ 1982–1992. Eur J Cancer 2000; 36: 901–908.
Cohn SL, Pearson AD, London WB, Monclair T, Ambros PF, Brodeur GM et al. The International Neuroblastoma Risk Group (INRG) classification system: an INRG Task Force report. J Clin Oncol 2009; 27: 289–297.
Volchenboum SL, Cohn SL . Are molecular neuroblastoma classifiers ready for prime time? Lancet Oncol 2009; 10: 641–642.
Janoueix-Lerosey I, Schleiermacher G, Michels E, Mosseri V, Ribeiro A, Lequin D et al. Overall genomic pattern is a predictor of outcome in neuroblastoma. J Clin Oncol 2009; 27: 1026–1033.
Vermeulen J, De Preter K, Naranjo A, Vercruysse L, Van Roy N, Hellemans J et al. Predicting outcomes for children with neuroblastoma using a multigene-expression signature: a retrospective SIOPEN/COG/GPOH study. Lancet Oncol 2009; 10: 663–671.
Oberthuer A, Juraeva D, Li L, Kahlert Y, Westermann F, Elis R et al. Comparison of the performance of one-color and two-color gene-expression analyses in predicting clinical endpoints of neuroblastoma patients. Pharmacogenomics J 2010; 10: 258–266.
Baldi P, Brunak S, Chauvin Y, Andersen CA, Nielsen H . Assessing the accuracy of prediction algorithms for classification: an overview. Bioinformatics 2000; 16: 412–424.
Ferri C, Hernández-Orallo J, Modroiu R . An experimental comparison of performance measures for classification. Pattern Recognit Lett 2009; 30: 27–38.
Cortes C, Mohri M . AUC optimization vs. error rate minimization. In: Thrun S, Saul L, Schoelkopf B (eds). Advances in Neural Information Processing Systems 16. The MIT Press: Cambridge, MA, 2004.
Chin SF, Wang Y, Thorne NP, Teschendorff AE, Pinder SE, Vias M et al. Using array-comparative genomic hybridization to define molecular portraits of primary breast cancers. Oncogene 2007; 26: 1959–1970.
Grutzmann R, Boriss H, Ammerpohl O, Luttges J, Kalthoff H, Schackert HK et al. Meta-analysis of microarray data on pancreatic cancer defines a set of commonly dysregulated genes. Oncogene 2005; 24: 5079–5088.
Laiho P, Kokko A, Vanharanta S, Salovaara R, Sammalkorpi H, Jarvinen H et al. Serrated carcinomas form a subclass of colorectal cancer with distinct molecular basis. Oncogene 2007; 26: 312–320.
Shimada H, Ambros IM, Dehner LP, Hata J, Joshi VV, Roald B et al. The International Neuroblastoma Pathology Classification (the Shimada system). Cancer 1999; 86: 364–372.
Brodeur GM, Maris JM, Yamashiro DJ, Hogarty MD, White PS . Biology and genetics of human neuroblastomas. J Pediatr Hematol Oncol 1997; 19: 93–101.
Caron H, van Sluis P, de Kraker J, Bokkerink J, Egeler M, Laureys G et al. Allelic loss of chromosome 1p as a predictor of unfavorable outcome in patients with neuroblastoma. N Engl J Med 1996; 334: 225–230.
Edsjo A, Nilsson H, Vandesompele J, Karlsson J, Pattyn F, Culp LA et al. Neuroblastoma cells with overexpressed MYCN retain their capacity to undergo neuronal differentiation. Lab Invest 2004; 84: 406–417.
Luttikhuis ME, Powell JE, Rees SA, Genus T, Chughtai S, Ramani P et al. Neuroblastomas with chromosome 11q loss and single copy MYCN comprise a biologically distinct group of tumours with adverse prognosis. Br J Cancer 2001; 85: 531–537.
Brodeur GM, Pritchard J, Berthold F, Carlsen NL, Castel V, Castelberry RP et al. Revisions of the international criteria for neuroblastoma diagnosis, staging, and response to treatment. J Clin Oncol 1993; 11: 1466–1477.
Beissbarth T, Speed TP . GOstat: find statistically overrepresented Gene Ontologies within a group of genes. Bioinformatics 2004; 20: 1464–1465.
Farina AR, Tacconelli A, Cappabianca L, Cea G, Chioda A, Romanelli A et al. The neuroblastoma tumour-suppressor TrkAI and its oncogenic alternative TrkAIII splice variant exhibit geldanamycin-sensitive interactions with Hsp90 in human neuroblastoma cells. Oncogene 2009; 28: 4075–4094.
Wai DH, Schaefer KL, Schramm A, Korsching E, Van Valen F, Ozaki T et al. Expression analysis of pediatric solid tumor cell lines using oligonucleotide microarrays. Int J Oncol 2002; 20: 441–451.
Thorell K, Bergman A, Caren H, Nilsson S, Kogner P, Martinsson T et al. Verification of genes differentially expressed in neuroblastoma tumours: a study of potential tumour suppressor genes. BMC Med Genomics 2009; 2: 53.
Lagergren A, Manetopoulos C, Axelson H, Sigvardsson M . Neuroblastoma and pre-B lymphoma cells share expression of key transcription factors but display tissue restricted target gene expression. BMC Cancer 2004; 4: 80.
Shimada H, Kuboshima M, Shiratori T, Nabeya Y, Takeuchi A, Takagi H et al. Serum anti-myomegalin antibodies in patients with esophageal squamous cell carcinoma. Int J Oncol 2007; 30: 97–103.
Rabenau KE, O’Toole JM, Bassi R, Kotanides H, Witte L, Ludwig DL et al. DEGA/AMIGO-2, a leucine-rich repeat family member, differentially expressed in human gastric adenocarcinoma: effects on ploidy, chromosomal stability, cell adhesion/migration and tumorigenicity. Oncogene 2004; 23: 5056–5067.
Chung S, Furihata M, Tamura K, Uemura M, Daigo Y, Nasu Y et al. Overexpressing PKIB in prostate cancer promotes its aggressiveness by linking between PKA and Akt pathways. Oncogene 2009; 28: 2849–2859.
Herath NI, Spanevello MD, Sabesan S, Newton T, Cummings M, Duffy S et al. Over-expression of Eph and ephrin genes in advanced ovarian cancer: ephrin gene expression correlates with shortened survival. BMC Cancer 2006; 6: 144.
Tomonaga T, Matsushita K, Yamaguchi S, Oohashi T, Shimada H, Ochiai T et al. Overexpression and mistargeting of centromere protein-A in human primary colorectal cancer. Cancer Res 2003; 63: 3511–3516.
Albino D, Scaruffi P, Moretti S, Coco S, Truini M, Di Cristofano C et al. Identification of low intratumoral gene expression heterogeneity in neuroblastic tumors by genome-wide expression analysis and game theory. Cancer 2008; 113: 1412–1422.
Li L, Hung AC, Porter AG . Secretogranin II: a key AP-1-regulated protein that mediates neuronal differentiation and protection from nitric oxide-induced apoptosis of neuroblastoma cells. Cell Death Differ 2008; 15: 879–888.
Puisieux A, Valsesia-Wittmann S, Ansieau S . A twist for survival and cancer progression. Br J Cancer 2006; 94: 13–17.
Sumantran VN, Brederlau A, Funa K . BMP-6 and retinoic acid synergistically differentiate the IMR-32 human neuroblastoma cells. Anticancer Res 2003; 23 (2B): 1297–1303.
Acknowledgements
This research was supported by Emory-Georgia Tech NCI Center for Cancer Nanotechnology Excellence (U54CA119338), NCI Bioengineering Research Partnership (R01CA108468), Georgia Cancer Coalition (Distinguished Cancer Scholar Award to MDW), National Science Foundation (Graduate Student Research Fellowship to RM), Microsoft Research and Hewlett-Packard.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Disclaimer The views presented in this article do not necessarily reflect those of the US Food and Drug Administration.
Supplementary Information accompanies the paper on the The Pharmacogenomics Journal website
Rights and permissions
This work is licensed under the Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Parry, R., Jones, W., Stokes, T. et al. k-Nearest neighbor models for microarray gene expression analysis and clinical outcome prediction. Pharmacogenomics J 10, 292–309 (2010). https://doi.org/10.1038/tpj.2010.56
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/tpj.2010.56
Keywords
This article is cited by
-
Integration of transcriptomic data identifies key hallmark genes in hypertrophic cardiomyopathy
BMC Cardiovascular Disorders (2021)
-
Identification of arthropathy and myopathy of the temporomandibular syndrome by biomechanical facial features
BioMedical Engineering OnLine (2020)
-
A recursive framework for predicting the time-course of drug sensitivity
Scientific Reports (2020)
-
An entropy-based classification of breast cancerous genes using microarray data
Neural Computing and Applications (2020)
-
Pattern analysis of genetics and genomics: a survey of the state-of-art
Multimedia Tools and Applications (2020)