Abstract
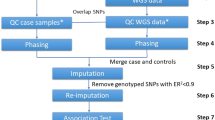
The Genome-Wide Association Working Group (GWAWG) is part of a large-scale effort by the MicroArray Quality Consortium (MAQC) to assess the quality of genomic experiments, technologies and analyses for genome-wide association studies (GWASs). One of the aims of the working group is to assess the variability of genotype calls within and between different genotype calling algorithms using data for coronary artery disease from the Wellcome Trust Case Control Consortium (WTCCC) and the University of Ottawa Heart Institute. Our results show that the choice of genotyping algorithm (for example, Bayesian robust linear model with Mahalanobis distance classifier (BRLMM), the corrected robust linear model with maximum-likelihood-based distances (CRLMM) and CHIAMO (developed and implemented by the WTCCC)) can introduce marked variability in the results of downstream case–control association analysis for the Affymetrix 500K array. The amount of discordance between results is influenced by how samples are combined and processed through the respective genotype calling algorithm, indicating that systematic genotype errors due to computational batch effects are propagated to the list of single-nucleotide polymorphisms found to be significantly associated with the trait of interest. Further work using HapMap samples shows that inconsistencies between Affymetrix arrays and calling algorithms can lead to genotyping errors that influence downstream analysis.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 6 print issues and online access
$259.00 per year
only $43.17 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout










Similar content being viewed by others
References
Donnelly P . Progress and challenges in genome-wide association studies in humans. Nature 2008; 456: 728–731.
Clayton DG, Walker NM, Smyth DJ, Pask R, Cooper JD, Maier LM et al. Population structure, differential bias and genomic control in large-scale, case-control association study. Nat Genet 2008; 37: 1243–1246.
Hong H, Su Z, Ge W, Shi L, Perkins R, Fang H et al. Assessing batch effect of genotype calling algorithm BRLMM for Affymetrix Genechip Human Mapping 500 K array set using 270 HapMap samples. BMC Bioinformatics 2008; 9 (Suppl 9): S17.
The Wellcome Trust Case Control Consortium. Genome-wide association study of 14 000 cases of seven common diseases and 3000 shared controls. Nature 2007; 447: 661–678.
Miclaus K, Vega S, Wolfinger R, Chierici M, Furlanello C, Lambert C et al. Batch effects in the BRLMM genotype calling algorithm influence GWAS results for the Affymetrix 500K array. TPJ 2010 (In Press).
Chierici M, Miclaus K, Vega S, Furlanello C . An interactive effect of batch size and composition contributes to discordant results in GWAS with the CHIAMO Genotyping Algorithm. TPJ 2010 (In Press).
Zhang L, Yin S, Miclaus K, Chierici M, Vega S, Lambert C et al. Assessment of variability in GWAS with CRLMM genotyping algorithm on WTCCC coronary artery disease. TPJ 2010 (In Press).
Affymetrix White Paper Publication. BRLMM: an improved genotype calling method for the genechip human mapping 500k array set http://www.affymetrix.com/support/technical/whitepapers/brlmmwhitepaper.pdf.
Lin S, Carvalho B, Cutler DJ, Arking DE, Chakravarti A, Irizarry RA . Validation and extension of an empirical Bayes method for SNP calling on Affymetrix microarrays. Genome Biol 2008; 9: R63.
Stewart AFR, Dandon S, Chen L, Assogba O, Belanger M, Ewart G et al. Kinesin family member 6 variant Trp719Arg does not associate with angiographically defined coronary artery disease in the Ottawa Heart Genomics Study. J Am Coll Cardiol 2009; 53: 1471–1472.
Hong H, Shi L, Su Z, Ge W, Jones W, Czika W et al. Assessing sources of inconsistencies in genotypes and their effects on genome-wide association studies with HapMap samples. TPJ 2010 (In Press).
The International HapMap Consortium. A second generation human haplotype map of over 3.1 million SNPs. Nature 2007; 449: 851–862.
Hochberg Y, Benjamini Y . More powerful procedures for multiple significance testing. Stat Med 1990; 9: 811–818.
Carvalho B, Louis TA, Irizarry RA . Quantifying uncertainty in genotype calls. Bioinformatics 2010; 26: 242–249.
Zaykin DV, Zhivotovsky LA . Ranks of genuine associations in whole-genome scans. Genetics 2005; 171: 813–823.
Kraft P, Zeggini E, Ioannidis JPA . Replication in genome-wide association studies. Stat Sci 2009; 24: 561–573.
Acknowledgements
We thank all members of the GWAWG and MAQC for their contribution to this article as well as the members of the WTCCC and Dr George Wells from the University of Ottawa Heart Institute for providing access to the data. We also thank the anonymous reviewers for their invaluable feedback, which has made this paper a much improved contribution.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Disclaimer
The views presented in this article do not necessarily reflect those of the US Food and Drug Administration.
Supplementary Information accompanies the paper on the The Pharmacogenomics Journal website
Supplementary information
Rights and permissions
About this article
Cite this article
Miclaus, K., Chierici, M., Lambert, C. et al. Variability in GWAS analysis: the impact of genotype calling algorithm inconsistencies. Pharmacogenomics J 10, 324–335 (2010). https://doi.org/10.1038/tpj.2010.46
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/tpj.2010.46
Keywords
This article is cited by
-
Identifying and mitigating batch effects in whole genome sequencing data
BMC Bioinformatics (2017)
-
KRLMM: an adaptive genotype calling method for common and low frequency variants
BMC Bioinformatics (2014)
-
Letter to the editor: expression of concern, reaffirmed
AGE (2014)