Abstract
The mutifractal and long range correlation (C(r)) properties of strings, such as nucleotide sequence can be a useful parameter for identification of underlying patterns and variations. In this study C(r) and multifractal singularity function f(α) have been used to study variations in the genomes of a pathogenic bacteria Mycobacterium tuberculosis. Genomic sequences of M. tuberculosis isolates displayed significant variations in C(r) and f(α) reflecting inherent differences in sequences among isolates. M. tuberculosis isolates can be categorised into different subgroups based on sensitivity to drugs, these are DS (drug sensitive isolates), MDR (multi-drug resistant isolates) and XDR (extremely drug resistant isolates). C(r) follows significantly different scaling rules in different subgroups of isolates, but all the isolates follow one parameter scaling law. The richness in complexity of each subgroup can be quantified by the measures of multifractal parameters displaying a pattern in which XDR isolates have highest value and lowest for drug sensitive isolates. Therefore C(r) and multifractal functions can be useful parameters for analysis of genomic sequences.
Similar content being viewed by others
Introduction
Genomic alteration through a number of mechanisms (mutation, substitution, duplication, deletion, insertion, and selection etc.) in combination with natural selection provides a basis of evolution. However, evolution does maintain some conserved features that are characteristics of the organisms. The generic features of these conserved properties can be characterized by the scaling laws1,2 emerging from one dimensional genome sequence. These laws are preserved and inherited in the complex evolutionary process. Scaling law of an observable y(x), which manifests preserved properties in the system, can be quantified through scaling functions F[x, y(x)] and Γ[y(x)]3,4, and follows self-affine process for any scale factor c5, given by

where, A is a constant, and D is the self-similarity dimension of the self-affine process. If this y(x) involves a few number of fractal rules then it obeys Mandelbrot’s classical multifractal rules for self-affine process6,

One of the conserved properties is genomic correlation function C(r) of the DNA sequence which follows the fractal rule7:  , with D = −ε. The value of D is different for different biological processes; for genome length distribution in unicellular organisms D = 1/48, for distribution of RNA concentration D = 1/48, for metabolic process D = −3/49, for heart rate D = 1/48, for life span of the organism D = −1/49, for the distribution of radii of aortas and tree trunks D = −3/89.
, with D = −ε. The value of D is different for different biological processes; for genome length distribution in unicellular organisms D = 1/48, for distribution of RNA concentration D = 1/48, for metabolic process D = −3/49, for heart rate D = 1/48, for life span of the organism D = −1/49, for the distribution of radii of aortas and tree trunks D = −3/89.
Multifractal properties of DNA can be characterized by long range correlation maintained in the whole genome7, and pseudorandom distribution of nucleotides10 following an overall probability distribution. These can be represented as a DNA walk in two dimensional space10,11. Even though multifractal detrended fluctuations analysis (MF-DFA) technique is particularly important for a varity of time series data analysis12, such as sunspot time series13, stock exchange rate time series data14, complicated earthquake data15, social and religious dynamics16, traffic flow time series17, energy stocks data18, brain EEG data19, human DNA sequence20, the application of this technique for analysis of Next Generation Sequencing (NGS) data of organisms for extraction of useful information may be challenging.
Mycobacterium tuberculosis is a slow growing pathogen that causes Tuberculosis (TB) and it is one of the major public health challange particularly among lower and middle income countries21,22. Drug resistance is one of the major concerns for treatment of patients with this disease and occurrence of extreme drug resistance (XDR) may make the scenario even worse. Drug resistant genes such as rpoB23,24, inhA25, katG26, gyrA27, ahpC28, embB29, pncA30 have been experimentally identified. Different isolates of this bacterium have been classified into various lineages using sequence features and these lineages show correlation with geographical location. Recent genomic studies have found relationship between sequence differences among different isolates (represented by single nucleotide polymorphisms or SNPs and different repetitive sequences) and lineages31,32. Drug resistance isolates can be classified into different categories depending upon level of resistance. Multi Drug Resistance isolates (MDR) are insensitive to a few drugs whereas XDR isolates are resistant to a number of drugs. In recent times there has been an increase in the number of patients infected with both MDR-TB and XDR-TB, over 480,000 people developed multidrug-resistance TB in 2014 22. India, the Russian Federation and the Peoples Republic of China reported half of the cases of MDR-TB and an estimate of around 9.7% of MDR-TB cases are likely to be also XDR-TB22. Changes in genomic sequences are not distributed randomly, some regions (hotspots) display high level of variations whereas a few others are highly conserved (coldspots)33. In our analysis we considered a few genes that display significant variations among drug resistant strains and are thought to be involved in drug resistance, such as rpoB, phoP and phoR. Sequences from some of these genes that map to the same strand of the genome from different M. tuberculosis isolates were concatenated to make a single sequence for multifractal analysis34. These sequences were obtained from NGS datasets of available isolates35,36. The results showed that C(r) and Multifractal analysis can be useful parameters for classification of drug resistant isolates.
Results and Discussion
Theory of multifractality in genome evolution
Genome alterations in M. tuberculosis, due to various internal and external factors (e.g. continuous encounter with drugs and immune response of the host), is associated with sequence changes that involve substitution with different nucleotide, insertion and deletion, expansion of repeats, recombination and activity of transposable elements. NGS has allowed rapid and inexpensive method of getting complete nucleotide sequence, however the sequences come out as short reads. The nucleotide variation in these isloates are found to be not uniform, and large variations occur in few regions (called hotspots)37 and few genes only23,24,25,26,27,28,29,30. One dimensional DNA walk38 is generated from the genome sequence { xi; i = 1, 2, …, N} of each isloate (Fig. 1, Fig. 2 uppermost panels), where xi = +1 for purine (A and G), and xi = −1 for pyrimidine (C and T)10. Major unaltered portion of the genome of each isolate maintains same long range correlation  as reference genome with observed root mean square fluctuations of DNA walk,
as reference genome with observed root mean square fluctuations of DNA walk,  , where, γ = 1/2 for long range (r → large), and short range (r→0); and γ ≠ 1/2 for infinite range r → ∞38 exhibiting multifractal nature5,6,12. The specific genomic portions of each isolate (concatenated similar drug resistant genes), where significant amount of alterations are exhibited as compared to reference genome, show long range correlations
, where, γ = 1/2 for long range (r → large), and short range (r→0); and γ ≠ 1/2 for infinite range r → ∞38 exhibiting multifractal nature5,6,12. The specific genomic portions of each isolate (concatenated similar drug resistant genes), where significant amount of alterations are exhibited as compared to reference genome, show long range correlations  7 (Fig. 1, Fig. 2 middle panels), with fluctuation function Fq(s) of order q (see Methods) obeying power law,
7 (Fig. 1, Fig. 2 middle panels), with fluctuation function Fq(s) of order q (see Methods) obeying power law,  (Fig. 1, Fig. 2 lower most panels), where, Hq is generalized Hurst exponent12, showing indication of multifractal nature in the genes.
(Fig. 1, Fig. 2 lower most panels), where, Hq is generalized Hurst exponent12, showing indication of multifractal nature in the genes.
(a) DNA walks of forty isloates each of DS, MDR and XDR of M. tuberculosis (panels of uppermost row). (b) Corresponding plots of correlation functions (C(r) versus r) of the three types of isloates (panels of middle row). Straight lines are power law fits on the data (for rpoB gene: DS:  ; MDR:
; MDR:  ; XDR:
; XDR:  and for phoPR gene complex: DS:
and for phoPR gene complex: DS:  ; MDR:
; MDR:  ; XDR:
; XDR:  ). (c) Plots of fluctuation function (
). (c) Plots of fluctuation function ( ) with respect to s for the corresponding three types of M. tuberculosis isloates showing power law nature (panels of lowermost or third row).
) with respect to s for the corresponding three types of M. tuberculosis isloates showing power law nature (panels of lowermost or third row).
(a) DNA walks of forty isloates each of DS, MDR and XDR of M. tuberculosis (panels of uppermost row). (b) Corresponding plots of correlation functions (C(r) versus r) of the three types of isloates (panels of middle row). Straight lines are power law fits on the data (for gyrBA: DS:  ; MDR:
; MDR:  ; XDR:
; XDR:  and for embCAB: DS:
and for embCAB: DS:  ; MDR:
; MDR:  ; XDR:
; XDR:  ). (c) Plots of fluctuation function (
). (c) Plots of fluctuation function ( ) with respect to s for the corresponding three types of M. tuberculosis isloates showing power law nature (panels of lowermost or third row).
) with respect to s for the corresponding three types of M. tuberculosis isloates showing power law nature (panels of lowermost or third row).
Since the differences in the phenotypic and genotypic characters of each and every isolates from the reference M. tuberculosis genome(H37Rv) are due to the variations in the sequences of few hotspots and genes, local scaling properties of highly polymorphic regions(HPR) which are concatenated similar drug resistant genes may provide the characteristics of the perturbation induced in the reference genome and gets adapted to it. Consider a DNA walk of a HPR which can be divided into m segments {ui; i = 1, 2, …, N}. Then the probability that the ith segment having length scale r can have Ni observations for large N, which is given by  , holds the following power law in the limit r → 039,
, holds the following power law in the limit r → 039,

where, α is Holder or singularity exponent40 which serves as the measure of crowding index in HPR. If N(r, α) is the number of segments in which Λi has singularity strength between α and α + Δα, then N(r, α) obeys39,

where, f(α) is the singularity function which can be related to the observable properties of a certain experimental measure. f(α) can also be known as fractal dimension of the set of segments with singularity strength α. It can be related to another important generalized dimension Dq of order q which can be defined by41,42,

Different values of Dq characterize distribution in the segments with different degree of clustering in it. For non-stationary DNA walk,  and
and  corresponds to fractal dimensions of most and least populated segments respectively. Dq can be related to f(α) by employing Legendre transformation to its expression, and can be obtained as39,43,44,
corresponds to fractal dimensions of most and least populated segments respectively. Dq can be related to f(α) by employing Legendre transformation to its expression, and can be obtained as39,43,44,

where, τ is another classical multifractal scaling exponent43,44.
For HPR, f(α) is singularity spectrum with  as width of the singularity spectrum, which is a quantitative multifractal strength. Further, f(α) → 0, if
as width of the singularity spectrum, which is a quantitative multifractal strength. Further, f(α) → 0, if  and
and  45,46. If the DNA walk is monofractal, Hq is independent of q, and so from (6), α = constant, τ(q) is linear function of q, and f(α) is constant with α.
45,46. If the DNA walk is monofractal, Hq is independent of q, and so from (6), α = constant, τ(q) is linear function of q, and f(α) is constant with α.
The calculated f(α) as a function of α for forty isolates each of DS, MDR and XDR of M. tuberculosis shows different maxima values of f(α), but shows similar structural behavior (Figs 3 and 4 upper panels). The average f(α) along α shows significant difference in three different type of isolates (DS, MDR and XDR), except average f(α) values of DS and MDR isolates are approximately overlapping(Figs 3 and 4 the panels in the first and third rows). The scaled behavior of f(α) with α for each type of isolate shows approximately similar nature (Figs 3 and 4 insets in the panels of first and third rows).
(a) Plots of singularity function f(α) of the three types of isolates with respect to α (panels of first row) and their Scaling of f(α) by choosing αc = 1.02275 using interpolation showing self-affine process of the isolates (inside box). (b) Properties of multifractal spectral parameters: behaviors of α0, Δα and χ as a function of isolates (colors show types of isolates).
(a) Plots of singularity function f(α) of the three types of isolates with respect to α (panels of first row) and their Scaling of f(α) by choosing αc = 1.02275 using interpolation showing self-affine process of the isolates (inside box). (b) Properties of multifractal spectral parameters: behaviors of α0, Δα and χ as a function of isolates (colors show types of isolates).
The complexity of the DNA walk can be measured by expanding the singularity function f(α) around α0, with f(α0) → fmax (maximum value of f(α)), by Taylor’s series,

where, ω is the degree of the truncated polynomial. Then fitting the f(α) data of DNA walk with the polynomial (7), the following multifractal parameters can be calculated: αo, αmin, αmax, and Δα = αmax − αmin. The symmetry of each singularity spectrum can be quantified by defining a skew parameter,

Small value of α0 correspond to more regular struture in the HPR14. Δα → large indicates stronger multifractality due to richness in structure of the genome. χ > 1 reveals the dominance of scaling by small fluctuations and higher Hurst exponents, and indicating the presence of fine structure process in the genome. However, χ < 1 indicates the dominance of scaling by large fluctuations of singular spectrum and relatively small Hurst exponents showing correlation in the signal corresponding to absence of fine structure process in the signal. Richness in complexity in the HPR corresponds to large value of α0, wide range of Δα, and χ > 114,47.
The nature of α0 for DS and MDR type of isolates are closely similar to each other. This similar behavior is due to the similarity in sequence variation in these two types of isolates, which exhibits similar multifractal behaviors (Figs 3 and 4 extreme left panels in second and fourth rows). The average values of α0 for the four genes in the three isolates DS, MDR and XDR are found to be different but follow similar behavior (Figs 3 and 4 fourth panels in second and fourth rows). Similar properties of these two types of isolates are also exhibited in the nature of Δα (Figs 3 and 4 second leftmost and fifth panels in second and fourth rows), and in the behaviour of χ (Figs 3 and 4 third leftmost and sixth panels in the second and fourth rows). Comparatively large values of Δα and χ values in XDR as compared to those of DS and MDR indicates significant richness in multifractality in XDR. Further, since χ < 1 (slightly left skewed) for all the three types of isolates, the sequence alteration in the HPR is due to genome evolution in M. tuberculosis. This induces large fluctuation in the singular function and small in Hurst exponents driving more correlation in the signal and causing destruction of fine structure process in the signal. Since the changes in these parameters are small, these sensitive parameters (α0, Δα and χ) can capture small changes in the multifractal nature due to few sequence alterations in the HPR significantly.
SNP based sequences of M. tuberculosis isolates show multifractal nature
The whole genome of each isolate is mapped to the reference genome, and the SNP are arranged in a string without changing their positions but removing the nucleotides in between any pair of SNPs in the genome. The constructed SNP based sequences have varied lengths depending on the isolates, ranging from 432 bp to 4000 bp in length. We look at the multifractal properties of these SNP based sequences to understand fundamental mechanism of genome evolution (See Table1 in Supplementary file).
DNA walks of these SNP based sequences exhibit different behaviors for the three different classes DS, MDR and XDR (Fig. 5 uppermost row, first three panels). The one dimensional correlation function C(r) of these SNP based sequences is calculated using the procedure of Messer et al.48 (see Methods). The calculated C(r)s of all forty isolates of each class are plotted together (Fig. 5 second row), and the data as a whole follows power law,
(a) DNA walks of forty isolates each of DS, MDR and XDR of M. tuberculosis (the first three panels of uppermost row). (b) Corresponding plots of correlation functions (C(r) versus r) of the three types of isolates (first three panels of second row). Straight lines are power law fits on the data (for DS:  ; MDR:
; MDR:  ; XDR:
; XDR:  ). (c) Plots of singularity function f(α) of the three types of isolates with respect to α (first three panels of third row). (d) Properties of multifractal spectral parameters: behaviors of α0, Δα and χ as a function of isolates (colors show types of isolates) in the bottom row.
). (c) Plots of singularity function f(α) of the three types of isolates with respect to α (first three panels of third row). (d) Properties of multifractal spectral parameters: behaviors of α0, Δα and χ as a function of isolates (colors show types of isolates) in the bottom row.

where, k indicates isolate types: k → s, m, x for DS, MDR and XDR respectively. The best fitted curve on the data with power law (9) gives different values of θk for different class. This power law behavior of C(r) versus r for individual as well as groups of isolates (DS, MDR, and XDR) are verified following a standard statistical fitting procedure49, and found that the p-values (statistical level of significance) of each fitting on the dataset is found to be more than predicted critical value (p−value > 0.1). This change in the θk could be due to changes in SNPs in the SNP based sequences of different types of isolates of M. tuberculosis.
The calculated singularity spectra f(α) as a function of α for various isolates in different types of isolates exhibit different structures (Fig. 5 third row). Calculated α0 for different types of isolates (Fig. 5 Lowermost row extreme left panel) shows comparatively large values as compared to those of HPR, indicating the possibility of associating complex multifractal features in the SNP based sequences. The range of singularity spectra Δα for the types of isolates are also significantly large showing wide range of multifractal nature (Fig. 5 Lowermost row third plot). The shape of singularity spectra of all the isolates of different classes are found to be right skewed (χ > 1) which are the signature of the existence of fine structures in the SNP based sequences due to rich complex multifractal behavior. Further, the values of α0, Δα and χ for XDR SNP based sequences are found to be approximately larger than the other types showing richer possession of multifractal properties.
Scaling in genomic correlation function
The changes in HPR and SNP based sequences in different isolates of DS, MDR and XDR are due to selection of M. tuberculosis that are undergone sequence changes allowing resistance to drugs in the course of time50. This selection process is the one that allows only some isolates with altered genotypic and phenotypic properties leading to genome evolution51,52. These changes are species specific and affected very much by many factors including host immune systems and climatic conditions53. The spatio-temporal alterations in sequences in the isolates due to sequence alterations (mutations, deletions, duplications, insertions, substitutions, selections) can be nicely modeled using the proposed sequence evolution model7,54, and some of the observables can be characterized by the dynamics of position dependent one dimensional sequence compositional correlation,  . Defining
. Defining  , where, PE and PE are joint probabilities of finding any two symbols equal and opposite in sign and following their own Master equations, one can arrive at the following evolutionary dynamics of C(r) for r ≫ 1 (long range correlation),
, where, PE and PE are joint probabilities of finding any two symbols equal and opposite in sign and following their own Master equations, one can arrive at the following evolutionary dynamics of C(r) for r ≫ 1 (long range correlation),

where, A and B are constants which are functions of the rate constants of sequence alterations. The solution of the equation (10) is given by,  ; with
; with  , where κ is a constant. The stationary (t → 0) long range C(r) follows power law as we have observed in the HPR and SNP based sequences (Figs 1, 2, 6 and 7) with
, where κ is a constant. The stationary (t → 0) long range C(r) follows power law as we have observed in the HPR and SNP based sequences (Figs 1, 2, 6 and 7) with  . Averaging the values of θks of different isolate types in HPR and SNP based sequences (Fig. 6 Fourth and fifth column panels) respectively, we observe that in long range regime (r ≫ 1):
. Averaging the values of θks of different isolate types in HPR and SNP based sequences (Fig. 6 Fourth and fifth column panels) respectively, we observe that in long range regime (r ≫ 1):
-
HPR:
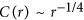 ; follows 1/4 scaling rule.
; follows 1/4 scaling rule. -
SNP based sequences:
 ; obeys 1/3 scaling law.
; obeys 1/3 scaling law.
(a) Scaling in rpoB gene for twenty isolates each of DS, MDR and XDR (panels of first row). The straight lines are power law fits to each isolate. The power law exponent (γ) for DS, MDR and XDR are given in rightmost panel of second row. The scaled data using Mackinnon and Kramer’s one parameter scaling procedure4 ( as a function of r, see Methods) is shown in first two panels of second row. (b) Same scaling procedure is done for SNP based sequences (panels of third and fourth row).
as a function of r, see Methods) is shown in first two panels of second row. (b) Same scaling procedure is done for SNP based sequences (panels of third and fourth row).
However, in short range regime (r ≪ 1) the nucleotides in the sequence follow Markov process7,55, and therefore C(r) decays with distance r of the nucleotide distribution,  , where, r0 is the characteristics length scale.
, where, r0 is the characteristics length scale.
The scaling behavior of the HPR can be studied by fitting the C(r) data of HPR of each isolate with equation (9) and analyzing the scaling nature. The fitted lines on the data of DS type (forty isolates) are approximately parallel (Fig. 6 extreme left panel of first row). These data can then be scaled together by using one parameter scaling procedure4,56 (see Methods) obeying  behavior (Fig. 6 fourth and fifth column panels). Applying the same one parameter scaling procedure, data of MDR and XDR isolates can also be scaled obeying
behavior (Fig. 6 fourth and fifth column panels). Applying the same one parameter scaling procedure, data of MDR and XDR isolates can also be scaled obeying  and
and  scaling rules respectively (Fig. 6 second, third and fourth column panels). These scaled data of DS, MDR and XDR can then be scaled together (Fig. 6 fourth and fifth column panels) following θ~1/4 scaling rule.
scaling rules respectively (Fig. 6 second, third and fourth column panels). These scaled data of DS, MDR and XDR can then be scaled together (Fig. 6 fourth and fifth column panels) following θ~1/4 scaling rule.
The same one parameter scaling procedure can also be done to the SNP based sequence data of DS, MDR and XDR isolates (Fig. 6 third and fourth rows). The scaled data follows θ~1/3 scaling law.
The scaling function Γ can be calculated in this regime using equation (1),

For short range correlated sequences (generated through Markov process),  48, and the scaling function can be obtained by,
48, and the scaling function can be obtained by,

The obeying of one parameter scaling law in NGS genome indicates the signature of self-organization in the system.
Classification of M. tuberculosis isolates
Different isolates(DS, MDR and XDR) can be classified based on the multifractal and correlation properties found in the corresponding HPR and SNP based sequences (Figs 3, 4, 5, 6 and 7). The average values of singularity spectral parameters of these isolates (Fig. 7) show significant differences: 1. For α0 (f(α0) → constant)  ; 2. For Δα (measure of multifractal complexity)
; 2. For Δα (measure of multifractal complexity)  , and 3. For χ (measure richness in multifractality)
, and 3. For χ (measure richness in multifractality)  . The nature of long range correlation function C(r) of these isolate types also exhibit significant behaviors (Fig. 7) as follows,
. The nature of long range correlation function C(r) of these isolate types also exhibit significant behaviors (Fig. 7) as follows,
-
For DS: correlation function in HPR follows,
 rule; and in SNP based sequences obeys
rule; and in SNP based sequences obeys  .
. -
For MDR: correlation function in HPR follows,
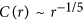 rule; and in SNP based sequences obeys
rule; and in SNP based sequences obeys  .
. -
For XDR: correlation function in HPR follows,
 rule; and in SNP based sequences obeys
rule; and in SNP based sequences obeys  .
.
The behaviors of Multifractal parameters in DS, MDR and XDR of M. tuberculosis are found to distinctly different given by:
-
For DS: HPR and SNP : Min[α0], Moderate[Δα, χ].
-
For MDR: HPR and SNP : Max[α0], Min[Δα, χ].
-
For XDR: HPR and SNP : Moderate[α0], Max[Δα, χ].
We classified the NGS sequences of M. tuberculosis based on these two distinct properties of Multifractal parameters and correlation function (Fig. 7).
Conclusion
The genome evolution in M. tuberculosis involves alteration of nucleotides in different isolates of DS, MDR and XDR. It is important to remember that genomic alterations continuously takes place and drugs tend to target isolates with appropriate sequence. Normally there are insignificant changes in most of the genome involved in house keeping function needed for the organism to survive and grow52. The significant alterations of nucleotides in the genomes of various isolates take place in few regions of the genomes called HPR (hotspots and concatenated genes)23,24,25,26,27,28,29,30,34,37. Few of these conserved properties are multifractal nature and correlation function which are being inherited by these isolates from the parent genome with modified rules.
The multifractal nature in the HPR of the different M. tuberculosis isolates are due to long range correlations with small and large fluctuations, and significant probability distributions in the genome. The singularity spectra of these HPR of the isolates is able to capture small range of multifractality from singularity spectral parameters leading to slightly ordered state, but far from monofractality.
The scenario of multifractal properties is quite different in SNP based sequences of these isolates which can provide overall properties of the modified genome. These SNP based sequences show rich and complex multifractal nature characterized by fine structures in the sequences. This rich multifractal nature in SNP based sequences shows the perturbation in the reference genome, with these modified rules (multifractal and correlation nature) within the multifractal boundary for a change for fit survival.
The long range correlation function of HPR and SNP based sequences of these isolates follow 1/4 and 1/3 scaling rules respectively. The rules in the correlation function may be different in these isolates, but this property is inherited during evolution. Further, the correlation functions in different isolates follow one parameter scaling law indicating that it is one of the properties which keeps genome integrity.
Methods
DNA walk of M. tuberculosis NGS data
The reads of the isolates of M. tuberculosis are downloaded from the Sequence Read Archive (SRA)35,36. Total 120 isolates are considered for our analysis. Forty isolates each from Drug sensitive (DS), Multi Drug Resitant (MDR) and Extremely Drug Resistant isolates (XDR) are considered. The reads are intially mapped to the reference genome H37Rv using BWA (Fig. 8)57. The BAM file is sorted using samtools and indexing of sorted bam file is performed58. In order to create a consensus sequence from the isolates the output of samtools mpileup is piped into bcftools view command, which in turn is piped into vcfutilis.pl program and finally a fastq file is created for the respective isolate. The fastq file is then converted into fasta file using seqtk program.
The fasta file is converted in DNA walk { } by considering purine (A and G) as step up (
} by considering purine (A and G) as step up ( = +1) and pyrimidine (C and T) as step down (xi = −1)38. The DNA walk is considered to be a non stationary time series data due to its stochastic behavior which in turn can be used for various properties using Multifractal Detrened Fluctuation Average (MFDFA) analysis using Matlab program59,60,61. The detail procedure is shown in a flowchart below8.
= +1) and pyrimidine (C and T) as step down (xi = −1)38. The DNA walk is considered to be a non stationary time series data due to its stochastic behavior which in turn can be used for various properties using Multifractal Detrened Fluctuation Average (MFDFA) analysis using Matlab program59,60,61. The detail procedure is shown in a flowchart below8.
Multifractal DFA approach
Multifractal detrended fluctuation analysis (MF-DFA) is a powerful technique to study fractal properties in nonstationary time series, and associated important correlations charactering the system39. Various important parameters which characterize the fractal nature of the time series and related properties, namely, Hurst exponent (H), generalized dimension (D), singularity spectrum (f) etc can be calculated numerically using a method adopted by Kantelhardt et al.12 as summerized below. Firstly, the time series signal  of length N is taken as random walk, and can be represented by the profile,
of length N is taken as random walk, and can be represented by the profile,  , where,
, where,  is mean value of the signal, and
is mean value of the signal, and  . Second, the profile Y(i) is now divided into
. Second, the profile Y(i) is now divided into  equal nonoverlapping equal segments of size s. To take into account all data points, 2Ns segments are considered by counting starting from both ends of the data. Third, the following variance is determined,
equal nonoverlapping equal segments of size s. To take into account all data points, 2Ns segments are considered by counting starting from both ends of the data. Third, the following variance is determined,

where,  , and
, and  is the fitting polynomial in segment ν. Fourth, the qth order fluctuation function is estimated by averaging over all segments,
is the fitting polynomial in segment ν. Fourth, the qth order fluctuation function is estimated by averaging over all segments,

Fifth, the scaling behavior of the function  is represented by,
is represented by,

where, Hq is the generalized Hurst exponent, which represents the measure of self-similarity and correlation properties of the signal. Then, Hq is related to classical scaling exponent τ(q) as,

and from the definition of Holder exponent,  , the singularity function
, the singularity function  39 is given by,
39 is given by,

Then, generalized fractal dimension of the signal is measured by,

Now, D0, for q = 0, is the fractal or Hausdorff dimension, D1 is information dimension and D2 represents correlation dimension39. Multifractal signature in the time series can be observed in the system if there exists significant dependence of Hq on q in the time series due to different scaling nature of small and large fluctuations12. Positive dependence of Hq on q indicates the scaling behavior of the time series segments with large fluctuations, whereas negative dependence of Hq on q exhibits scaling behavior in the time series segments with small fluctuations. Further, in multifractal time series, small and large fluctuations are characterized by large and small values of  .
.
Procedure for generating correlation function data
Correlation function  of one dimensional genomic sequence
of one dimensional genomic sequence  of length
of length  can be calculated following Messer et al. procedure7 defined by,
can be calculated following Messer et al. procedure7 defined by,

where,  is the probability of finding a base m at position k in the genomic sequence, and
is the probability of finding a base m at position k in the genomic sequence, and  is the conditional probability to find the same base m at a distance r from k.
is the conditional probability to find the same base m at a distance r from k.
One parameter scaling law in correlation function
The calculated correlation function C(r) of HPR of different isolates of NGS data of M. tuberculosis, where significant variation of sequences take place (hotspots and genes), follow power law behavior with approximately parallel fitted lines on HPR of different isolates (Fig. 2). This power law fitting on the data is verified and confirmed by following the fitting procedure proposed by Clauset et al.62, where the value of p (statistical significant level) of each fitting is found to be larger than 0.1 which is the critical value of verifying that each data follow power law. We then follow one parameter scaling theory3,4,56 to scale the data given by

where F is a scaling function. The form of the scaling function F and values of scaling exponent θ for DS, MDR and XDR isolates can be obtained by scaling the data of these isolates by fitting on the scaled data. Following this scaling procedure, and with the choice of ξ, we found that F → constant and obtained the following scaling law:

where  for HPR and SNP based sequence of different isolates of DS, MDR and XDR respectively.
for HPR and SNP based sequence of different isolates of DS, MDR and XDR respectively.
Datasets
NGS datasets were downloaded from European Nucleotide Archive(ENA), EMBL. In Supplementary file Accession numbers and isolate Names are mentioned. Some SNP sequences were downloaded from Genome-based Mycobacterium Tuberculosis Variation (GMTV) Database.
Additional Information
How to cite this article: Mandal, S. et al. Complex multifractal nature in Mycobacterium tuberculosis genome. Sci. Rep. 7, 46395; doi: 10.1038/srep46395 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Kadanoff, L. P. Scaling laws for Ising models near T c . Phys. 2, 263–272 (1966).
West, G. B. & Brown, J. H. Life’s universal scaling laws. Phys. Today 57, 36–42 (2004).
Abrahams, E., Anderson, P. W., Licciardello, D. C. & Ramakrishnan, T. V. Scaling Theory of Localization: Absence of Quantum Diffusion in Two Dimensions. Phys. Rev. Lett. 42, 673 (1979).
Mackinnon, A. & Kramer, B. The scaling theory of electrons in disordered solids: additional numerical results. Z. Phys. B. 53, 1–13 (1983).
Stoyan, D. & Mandelbrot, B. B. Fractals: Form, Chance, and Dimension. San Francisco. W. H. Freeman and Company. 1977. 352 S., 68 Abb., $14.95. ZAMM Journal of Applied Mathematics and Mechanics/Zeitschrift fr Angewandte Mathematik und Mechanik 59, 402–403 (1979).
Calvert, L., Fisher, A. & Mandelbrot, B. The Multifractal Model of Asset Returns. Discussion papers of the Cowles Foundation for Economics. Yale University: Cowles Foundation 114–1166, 12–27 (1997).
Messer, P. W., Arndt, P. F. & Lassig, M. Solvable sequence evolution models and genomic correlations. Phys. Rev. Lett. 94, 138103 (2005).
Savage et al. Func. Ecol. 18, 257 (2004).
West, G. B., Woodroff, W. H. & Brown, J. H. Proc. Natl. Acad. Sci. USA 99, 2473 (2002).
Gates, M. A. A simple way to look at DNA. Journal of Theoretical Biology 119, 319–328 (1986).
Liaofu, L. & Lu, T. Fractal dimension of nucleic acid sequences and the relation to evolutionary level. Chin. Phys. Lett. 5, 421–423 (1988).
Kantelhardt, Jan W. et al. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A: Statistical Mechanics and its Applications 316, 87–114 (2002).
Movahed, M. S., Jafari, G. R., Ghasemi, F., Rahvar, S. & Tavar, M. R. R. Multifractal detrended fluctuation analysis of sunspot time series. Journal of Statistical Mechanics: Theory and Experiment 02 (2006).
Darko, S., Dusan, S., Tatijana, S. & Stanley, H. E. Multifractal analysis of managed and independent float exchange rates. Physica A 428, 13–18 (2015).
Flores-Marquez, E. L., Ramirez-Rojas, A. & Telesca, L. Multifractal detrended fluctuation analysis of earthquake magnitude series of Mexican South Pacific Region. Appl. Math. Compt. 265, 1106–1114 (2015).
Rotundo, G., Ausloos, M., Herteliu, C. & Ileanu, B. Hurst exponent of very long birth time series in XX century Romania, Social and religious aspects. Physica A 429, 109–117 (2015).
Yin, Y. & Shang, P. Multiscale multifractal detrended cross-correlation analysis of traffic flow. Nonlinear Dyn. 81, 1329–1347 (2015).
Yang, L., Zhu, Y. & Wang, Y. Multifractal characterization of energy stocks in China: a multifractal detrended fluctuation analysis. Physica A 451, 357–365 (2016).
Maity, A. K., Pratihar, R., Mitra, A., Dey, S., Agrawal, V., Sanyal, S., Banerjee, A., Sengupta, R. & Ghosh, D. Multifractal detrended fluctuation analysis of alpha and theta EEG rhythms with musical stimuli. Chaos, Solitons and Fractals 81, 52–67 (2015).
Moreno, P. A., Patricia, E. V., Ember, M., Luis, E. G., Daz, N., Siler, A., Irene, T., Jos, M. G., Ashwinikumar, K. N., Tobar, F. & Felipe, G. The human genome: a multifractal analysis. BMC Genomics 12, 506 (2011).
Cole, STea et al. Deciphering the biology of Mycobacterium tuberculosis from the complete genome sequence. Nature 393, 537–544 (1998).
World Health Organization. Global Tuberculosis Report 2015, 20th edition(2015).
Telenti, Amalio et al. Detection of rifampicin-resistance mutations in Mycobacterium tuberculosis. The Lancet 341, 647–651 (1993).
Telenti, Amalio et al. Direct, automated detection of rifampin-resistant Mycobacterium tuberculosis by polymerase chain reaction and single-strand conformation polymorphism analysis. Antimicrobial Agents and Chemotherapy 37, 2054–2058 (1993).
Banerjee, Asesh et al. inhA, a gene encoding a target for isoniazid and ethionamide in Mycobacterium tuberculosis. Science 263, 227–230 (1994).
Zhang, Ying et al. The catalase-peroxidase gene and isoniazid resistance of Mycobacterium tuberculosis. Nature 358, 591–593 (1992).
Takiff, Howard E. et al. Cloning and nucleotide sequence of Mycobacterium tuberculosis gyrA and gyrB genes and detection of quinolone resistance mutations. Antimicrobial agents and chemotherapy 38, 773–780 (1994).
Sherman, David R. et al. Compensatory ahpC gene expression in isoniazid-resistant Mycobacterium tuberculosis. Science 272, 1641–1643 (1996).
Telenti, A., Philipp, W. J., Sreevatsan S. et al. The emb operon, a gene cluster of Mycobacterium tuberculosis involved in resistance to ethambutol. Nat Med 3, 567–70 (1997).
Scorpio, A. & Zhang, Y. Mutations in pncA, a gene encoding pyrazinamidase/nicotinamidase, cause resistance to the antituberculous drug pyrazinamide in tubercle bacillus. Nat Med 2, 662–7 (1996).
Comas, I. et al. Human T cell epitopes of Mycobacterium tuberculosis are evolutionarily hyperconserved. Nat Genet 42, 498–503 (2010).
Feuk, L., Carson, A. R. & Scherer, S. W. Structural variation in the human genome. Nature Reviews Genetics 7, 85–97 (2006).
Koutras, M. V., Bersimis, S. & Maravelakis, P. E. Statistical Process Control using Shewhart Control Charts with Supplementary Runs Rules. Methodology and Computing in Applied Probability 9, 207–224 (2007).
Walters, Shaun B. et al. The Mycobacterium tuberculosis PhoPR two component system regulates genes essential for virulence and complex lipid biosynthesis. Molecular microbiology 60, 312–330 (2006).
Leinonen Rasko, Hideaki Sugawara & Martin Shumway . The sequence read archive. Nucleic acids research gkq1019(2010).
Chernyaeva, Ekaterina N. et al. Genome-wide Mycobacterium tuberculosis variation (GMTV) database: a new tool for integrating sequence variations and epidemiology. BMC genomics 15, 308 (2014).
Das, Sarbashis et al. Identification of Hot and Cold spots in genome of Mycobacterium tuberculosis using Shewhart Control Charts. Scientific reports 2 (2012).
Peng, C. K., Buldyrev, S. V., Goldberger, A. L., Havlin, S., Sciortino, F., Simons, M. & Stanley, H. E. Long-range correlations in nucleotide sequences. Nature 356, 168–170 (1992).
Halsey, Thomas C. et al. Fractal measures and their singularities: the characterization of strange sets. Physical Review A 33, 1141 (1986).
Mallat, S. & Hwang, W. L. Singularity detection and processing with wavelets. IEEE Trans. Infor. Theor. 28, 617 (1992).
Hentschel, H. & Procaccia, I. Physica D 8, 435–444 (1983).
Grassberger, P. Phys. Lett. A 97, 227–230 (1983).
Feder, J. Fractals, Plenum Press, New York 9 (1988).
Peitgen, H.-O., Jurgens, H. & Saupe, D. Chaos and Fractals, Springer, New York (1992).
Kantelhardt, J. W., Eva, K.-B., Rybski, D., Braum, P. Bunde, A. & Havlin, S. Long-term persistence and multifractality of precipitation and river runoff records. J. Geophys. Res. 111, D01106 (2006).
Norouzzadeh, P. & Rahmani. Physica A 367, 328 (2006).
Shimizu, Y., Thurner, S. & Ehrenberger, K. Multifractal spectra as a measure of complexity in human posture. Fractals 10, 103 (2002).
Messer, P. W., Bundschuh, Vingron, M. & Arndt, P. F. Effects of Long-Range Correlations in DNA on Sequence Alignment Score Statistics. J. Compt. Biol. 14, 655–668 (2007).
Clauset, A. et al. Power-law distributions in empirical data. SIAM Rev. Soc. Ind. Appl. Math. 51, 661–703(2009).
Gandhi, N. R., Paul, N., Keertan, D., Schaaf, H. S., Matteo, Z., Soolingen, D. V., Jensen, P. & Bayona, J. Lancet 375, 1830–1843 (2010).
Holland, John H. & Hidden, H. Order: how adaptation builds complexity. Basics Book(1996).
Heylighen, F. The science of self-organization and adaptivity. The encyclopedia of life support systems 5, 253–280 (2001).
Frieden, T. R., Sterling, T., Ariel, P.-M., Kilburn, J., Cauthen, G. M. & Dooley, S. W. The emergence of drug-resistant tuberculosis in New York city. New England J. Med. 328, 521–526 (1993).
Saakian, D. B. Evolution models with base substitutions, insertions, deletions and selection. Phys. Rev. E 78, 061920 (2008).
Bernaola-Galvan, P., Carpena, P., Roman-Roldan, R. & Oliver, J. L. Gene 300, 105–115 (2002).
Pichard, J. L. & Sarma, G. Finite size scaling approach to Anderson localisation. J. Phys. C 14, L127–L132 (1981).
Li, H. & Durbin, R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25, 1754–1760 (2009).
Li, Heng et al. The sequence alignment/map format and SAMtools. Bioinformatics 25, 2078–2079 (2009).
Gu, Gao-Feng & Wei-Xing, Zhou . Detrending moving average algorithm for multifractals. Physical Review E 82, 011136 (2010).
Ihlen, Espen A. F. Introduction to multifractal detrended fluctuation analysis in Matlab. Fractal Analyses: Statistical And Methodological Innovations And Best Practices 97 (2012).
Xu, Limei et al. Quantifying signals with power-law correlations: A comparative study of detrended fluctuation analysis and detrended moving average techniques. Physical Review E 71, 051101 (2005).
Clauset, A., Shalizi, C. R. & Newman, M. E. J. Power-law distributions in empirical data. SIAM Rev. Soc. Ind. Appl. Math. 51, 661–703 (2009).
Acknowledgements
S.M. is financially supported by Council of Scientific and Industrial Research (CSIR) through JRF (Junior Research Fellowship), under award no. 09/263(1015)/2014-EMR-I. R.K.B.S. is financially supported by Department of Science and Technology (DST), New Delhi, India, under sanction no. SB/S2/HEP-034/2012. S.M. would like to thank Soibam Shyamchand Singh for his valuable discussion.
Author information
Authors and Affiliations
Contributions
S.M. and R.K.B.S. conceived the model. S.M. did the numerical experiment and prepared the figures of the numerical results. R.K.B.S. and S.M. analyzed and interpreted the simulation results, and wrote the manuscript. T.R.C. generated SNP data. S.M., T.R.C., K.C., A.B., and R.K.B.S. are involved in the study, reviewed and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Mandal, S., Roychowdhury, T., Chirom, K. et al. Complex multifractal nature in Mycobacterium tuberculosis genome. Sci Rep 7, 46395 (2017). https://doi.org/10.1038/srep46395
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep46395
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.








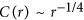 ; follows 1/4 scaling rule.
; follows 1/4 scaling rule. ; obeys 1/3 scaling law.
; obeys 1/3 scaling law.

 rule; and in SNP based sequences obeys
rule; and in SNP based sequences obeys  .
.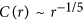 rule; and in SNP based sequences obeys
rule; and in SNP based sequences obeys  .
. rule; and in SNP based sequences obeys
rule; and in SNP based sequences obeys  .
.