Abstract
The resolution of conventional terahertz (THz) imaging techniques is limited to about half wavelength, which is not fine enough for applications of biomedical sensing and nondestructive testing. To improve the resolution, a new superlens, constructed by a monolayer graphene sheet combining with a grating voltage gate, are proposed in this paper to achieve deep super-resolution imaging in the THz frequency range. The main idea is based on the Fabry-Perot resonance of graphene edge plasmon waves. By shaping the voltage gate into a radial pattern, magnified images of subwavelength targets can be obtained. With this approach, the finest resolution can achieve up to λ/150. Besides, the superlens can be conveniently tuned to work in a large frequency band ranging from 4.3 THz to 9 THz. The proposal could find potential applications in THz near-field imaging systems.
Similar content being viewed by others
Introduction
In recent years, terahertz (THz) imaging applications1 have received constantly growing interest due to the capability of THz waves to penetrate a wide range of materials2. However, the resolution of conventional THz imaging techniques are limited to millimeter range3, owing to the evanescent decay of high spatial frequencies away from their source, the fact of which is also well known as the diffraction limit4. Even though THz near-field scanning imaging systems5,6,7 can achieve nanometer scale spatial resolution by using probes with sharp tips, the whole process of image reconstruction is troublesome and time-wasting since the point by point detection needs to be performed. The proposal of optical superlens8,9,10 constructed by negative index metamaterials or plasmonic materials (such as silver) targets to realize real-time super-resolution imaging. The collective oscillating of electrons in silver, known as surface plasmon polaritons (SPPs)11, would result amplification of the evanescent spatial frequencies. Nevertheless, experiments show that SPPs in silver become very weak12 in the THz frequency range. This is the main obstacle when we extend the working frequency of superlens and hyperlens13,14 to THz frequencies. Since the internal images of objects can be glimpsed owing to the penetrability of THz waves, realizing super-resolution imaging in the THz frequency range shows its special advantages on applications such as biomedical sensing15 and nondestructive testing16. By periodically perforating subwavelength square holes17 or embedding subwavelength grooves18 in metals, mimicking SPPs can be generated at THz frequencies. Structures based on this kind of metastructures have been well designed to break the diffraction limit19,20.
Graphene, emerged as the most promising 2D plasmonic material in the THz to mid-infrared frequency range21, has become an ideal candidate for designing plasmonic devices22. Compared with the mimicking SPPs, graphene plasmons show the superiority on tunability by chemical doping or gate voltage23. By dynamically tuning the conductivity of graphene, a planar gradient index graphene-based lens is designed to control the SPPs beam deflections24 or focusing25. In addition, significant enhancements of evanescent waves for near-field subwavelength imaging are demonstrated by a monolayer graphene26 and layered graphene24,27,28. More importantly, hyperlenses constructed by a modulated graphene monolayer29 or graphene/dielectric multilayers30 are also explored to realize subwavelength imaging at THz frequencies. But the hyperlenses cannotrealize frequency tuning conveniently, this is the inherent drawback of the constructed structures with hyperbolic isofrequency contour.
In this paper, a new graphene-based superlens is proposed to break the diffraction limit in the THz frequency range. The superlens is composed by a monolayer graphene sheet and a metallic grating voltage gate. The working mechanism of the superlens relies on Fabry-Perot resonance of graphene edge plasmon waves. The working frequency can be conveniently tuned over a large range by changing the gate voltage. Furthermore, magnified images of subwavelength targets can be obtained if we shape the voltage gate into a radial pattern. A deep resolution of 400 nm is demonstrated, which indicates our proposal could be suitable for biomedical applications.
Results
Graphene Plasmons
The schematic of the near-field superlens is illustrated in Fig. 1(a). A monolayer graphene sheet is supported on a SiO2 substrate. The permittivity of the SiO2 is 3.9. On the back of the substrate, there is a metallic grating voltage gate. Different separations between the graphene and the metallic surface of the grating lead to non-uniform modification of the carrier density, which eventually generates the periodical conductivity along the x direction. This is now a common method used for tuning the conductivity of graphene31. As we know, the complex conductivity of graphene, expressed as σg = σg,r + iσg,i, depends on angular frequency ω, electron relaxation time τ representing the loss mechanism, temperature T, and chemical potential μc. The imaginary part of the conductivity determines the propagation of SPPs waves, the real part of the conductivity represents the losses. When σg,i > 0, a single free-standing layer of graphene effectively behaves as a very thin “noble metal” layer with negative permittivity. Hence, the graphene sheet can surppot a transverse-magnetic (TM) polairized SPPs surface wave. The dispersion of the two dimensional graphene surface plasmon (2DGSP) supported on the sheet can be expressed as32
(a) is the real model. A monolayer graphene sheet is supported on the SiO2 substrate and the conductivity of the sheet is periodically tuned by a grating voltage gate. (b) is the equivalent model at a given frequency. The graphene ribbons correspond to the regions in the graphene sheet with high conductivity.

where εr1 and εr2 are the relative permittivity of the dielectrics above (here it is the air) and under the graphene sheet, ε0 is the permittivity in vacuum, e is the electron charge, ħ is the Plank’s constant. qp represents the in-plane wave-vector of the plasmon waves.
For the model in Fig. 1(a), the spatial period of the conductivity is p, corresponding to the period of the grating. We assume the conductivities of the two adjacent regions (regions 1 and 2) are respectively σg1 and σg2. If the conditions that Im(σg1) > 0 and Im(σg2) < 0 or Im(σg2) ≪ Im(σg1) are fulfilled, Fresnel reflection will occur on the boundary of the two regions. Hence, the surface waves will be confined to a fictitious boundary33,34. It gives a simple explanation of how the SPPs edge mode being excited. Different from the 2DGSP, the edge mode has maxima of intensity near the boundaries. Such one-dimensional (1D) excitations are generic for thin lossy metal films with finite width, although their dispersion depends on the thickness and the dielectric environment of the edge35. The 1D edge mode is also theoretically and experimentally observed on a graphene ribbon or a ribbon array36,37. Actually, a graphene ribbon can be either a real graphene strip or something that is “virtually” created by spatially varying external gates acting on a graphene sheet, as proposed in ref. 34. In this way, the physical model of the superlens is equivalent to the model in Fig. 1(b) at a given frequency point. The graphene ribbon array in Fig. 1(b) corresponds to the regions in the graphene sheet with the conductivity being σg1. The width of the ribbons is d, and the duty ratio is 0.5. Below, we will use this equivalent model to present the analysis. Although the microscopic structure of graphene edges modifies the electronic spectrum significantly, the excitation of the edge mode depends only on total charges and total currents. When the separation between the Femi energy and the Dirac point is much larger than the temperature or relaxation energy, the nature of what kind of edge does not affect the calculations reported here34.
It has been well demonstrated that the wavelengths of the 1D edge plasmons (λep) and the 2D surface plasmons (λp) differ by a universal numerical factor37, i.e. λep = C0·λp, where C0 is the factor, λp = 2π/Re(qp). The value of C0 increases with the width of the ribbon, but we always have C0 < 1. The physical reason for the smaller wavelength of the edge plasmons compared to the 2D ones is the effective reduction of the Drude weight at the edges, where free carriers exist only on “one side”. The electric field of the edge plasmons decays exponentially away from the edge. For a given ribbon width, high order modes, which are actually the hybrids of 1D edge mode and 2DGSP mode, can be excited at large frequencies. But the 2DGSP mode disappears at low frequencies. Each of the high order modes has a cutoff frequency. Hence, there is always a frequency band for the single fundamental mode (i.e. the 1D edge mode) operation. The narrower the width of the ribbon is, the broader the frequency band will be. In the frequency range we concerned, the condition of single fundamental mode operation is always satisfied by cutting down the width of ribbons to nanometer scale (much smaller than the wavelength).
The dispersion of graphene ribbons has been extensively studied by a variety of theories such as the theory of the hydrodynamics of electron-hole liquid33. A simple electrostatic scaling law reported in ref. 38 can also be used to quantitatively obtain the universal plasmon dispersion curves. The plasmon frequencies have an analytical expression of

In equation (2), η is the scaling parameter which is only a function of the product qep d, where qep is the wave-vector of the edge mode. For an arbitrary d, the value of η could be analytically fitted by the simulated data of a given ribbon. By this way, we can obtain the dispersion curves corresponding to different graphene ribbons.
The numerical calculations are performed with the help of the finite elements methods using Comsol Multiphysics. The parameters of the graphene ribbon are chosen to be uc = 0.15 eV, τ = 0.5 ps at room temperature T = 300 K (the values of τ and T keep no change throughout the paper). These parameters are typical for graphene plasmons observed in THz to infrared frequency range32,34. The simulated plasmon wavelength λep is calculated by 2(DR-DL), DR and DL are respectively the right and the left positions of two adjacent peaks, as illustrated in the inset of Fig. 2. Both the simulated (dots) and fitting (solid lines) dispersion curves for three ribbons with d = 0.2 μm, 1 μm and 2 μm are presented in Fig. 2. We notice that, at a given frequency, if d decreases, the wavelength of the edge mode becomes shorter, which means that the 1D localized mode is more confined to the rims (the decrease of λep corresponds to the increase of qep, therefore, the surface wave decays faster). As we can observe, in the lower frequency range, the gap of the plasmon wavelengths between the edge mode supported on the nanoribbon and the 2DGSP (shown with red solid line in Fig. 2) supported on a graphene sheet is apparent. As shown in Fig. 2, the analytical fitting curves match well with the simulated data.
Near-Field Super-Resolution Imaging
For the graphene nanoribbon array shown in Fig. 1(b), each of the nanoribbons could be regarded to a transmission path of the edge mode. The whole system is similar to metal films with a periodic arrangement of cut-through slits39. The nanoribbons correspond to the subwavelength slits. The presences in the silts are TEM modes, but the presences on the nanoribbons are the edge modes. The electric field of the edge mode is expressed as  , where
, where  represents the transverse mode pattern. When a monochromatic plane wave with its x-direction wave-vector being kx impinges upon the front interface of the nanoribbon array, the edge modes will be excited with different initial phases (could be known by (kx ± 2nπ/p)·m′p) and propagate along each of the nanoribbons, n and m′ are both integers and refers to the n-order harmonic and the m′-th nanoribbon respectively counting from left to right. One of the electric field components on the m-th nanoribbon can be mathematically expressed as
represents the transverse mode pattern. When a monochromatic plane wave with its x-direction wave-vector being kx impinges upon the front interface of the nanoribbon array, the edge modes will be excited with different initial phases (could be known by (kx ± 2nπ/p)·m′p) and propagate along each of the nanoribbons, n and m′ are both integers and refers to the n-order harmonic and the m′-th nanoribbon respectively counting from left to right. One of the electric field components on the m-th nanoribbon can be mathematically expressed as

in which, r and Δφ are respectively the reflection coefficient and the phase jump of the reflected surface wave at the boundary, Δφ = tan−1[Im(r)/Re(r)], E0 is related to the coupling strength. As can be observed, regardless of the angle of the oblique incidence (including the evanescent harmonics), the incident plane waves will always be coupled to the graphene edge mode with the same longitudinal wave-vector, i.e. qep. Hence, the phase accumulations of any incident waves are the same at the emergence interface of the graphene nanoribbon array. The scattering waves of subwavelength targets are an integration of all spatial harmonics with corresponding amplitudes and phases. In order to obtain an undistorted image of the targets, the amplitude and the phase at the emergence interface must keep synchronous with the amplitude and phase at the incoming interface. Under this requirement, we can deduce the following equation after considering the boundary condition at both the incoming and the emergence interfaces

where lg is the length of the nanoribbons. Equation (4) can be satisfied if

Equation (5) is the Fabry-Perot resonance condition30,40. We conclude that the subwavelength targets can be resolved at the emergence interface only when the Fabry-Perot resonance of the edge mode is set up. After substituting Δφ and qep into equation (5), we can calculate the value of lg. An analytical method to determine Δφ has been reported in ref. 40, and it is claimed that Δφ is approximately constant during a broadband frequency range. For simplicity here, we can determine Δφ by numerical simulation. When the parameters of the nanoribbons are uc = 0.15 eV and d = 0.2 μm, we get Δφ ≈ 0.54π in the 4 THz-9 THz frequency range. When the working frequency is chosen to be f = 5 THz, we have qep = 46.12k0, in which k0 is the wave-vector in free space. The conductivity of the graphene nanoribbons at 5 THz is σg1 = 0.035 + i0.56 mS. For m = 2, we obtain lg = 0.95 μm.
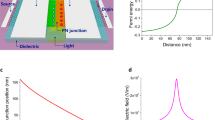
Next, numerical simulation using Comsol is performed to demonstrate the super-resolution imaging of the superlens. In Fig. 3(a), the near-field 2D images (electric field mapping on the x-z plane) of two targets are presented. Here, the targets are surface current sources with their directions parallel to z-axis. The x-direction width of the targets is 250 nm. The two targets are separated by 650 nm and located 60 nm away from the incoming interface. The 2D images are detected at the distance of 60 nm away from the emergence interface. As the above theory predicted, the two subwavelength targets are able to be perfectly distinguished in the near-field by the graphene superlens. The x-y plane electric field mapping above the graphene is shown in Fig. 3(b), from which we can observe the transmissions of the edge modes. In this case, the λ/92 imaging resolution is demonstrated. The near-field 2D images of the two incident targets which are separated 400 nm are illustrated in Fig. 3(c), the x-y plane electric field mapping is illustrated in Fig. 3(d). The two obvious peaks corresponding to the two targets also demonstrate the performance of the superlens. The imaging resolution in this case is λ/150. Theoretically speaking, this is the ultimate resolution of the designed graphene superlens because the resolution cannot be smaller than the period of the nanoribbon array. To improve the resolution, one can further narrow the width of the nanoribbons.
(a,b) are respectively the electric field mapping on x-z plane and x-y plane. The two sources are separated by 650 nm. (c,d) are respectively the electric field mapping on x-z plane and x-y plane. But the distance of the two sources changes to be 400 nm. (e) presents the simulation on a monolayer graphene sheet. The two sources are separated by 800 nm. (f) presents the simulated electric field when lg changes to be 0.95 μm. (g) is the normalized image of the line current sources when the length of the graphene ribbons are lg = 0.95 μm, 1.53 μm, 2.12 μm, respectively corresponding to the 2nd, the 3rd and the 4th Fabry-Perot resonance. The electric field mapping of the 3rd Fabry-Perot resonance is shown in the inset.
Even though all of the above simulations are done on the graphene nanoribbons array, the same results will be obtained if we replace the graphene nanoribbons with a monolayer graphene sheet tuned by a grating voltage gate. At 5 THz, we have Im(σg1) = 0.56 mS and Im(σg2) = 0.0012 mS. The two targets are separated by 800 nm. As shown in Fig. 3(e), the x-y plane electric field mapping in this case is almost the same as Fig. 3(b). To further verify the role of the Fabry-Perot resonance, we simulate a case of that the Fabry-Perot resonance condition is not satisfied. As presented in Fig. 3(f), the y-direction length of the graphene sheet (or nanoribbons) is lg = 1.15 μm, the images of the two targets are disturbed. Hence, we cannot simply regard each of the nanoribbons as a field probe. When lg = 1.53 μm, as shown in the inset of Fig. 3(g), the images are reconstructed again because the 3rd order (m = 3) Fabry-Perot resonance is established. The normalized 1D images corresponding to the 2nd, the 3rd and the 4th order Fabry-Perot resonance, plotted along a x-direction line which is 60 nm away from the emergence interface, are also shown in Fig. 3(g). The lengths of the superlenses are lg = 0.95 μm, 1.53 μm, 2.12 μm, respectively corresponding to m = 2, 3, 4 in equation (5). Now, we can see the key role of the Fabry-Perot resonance in determining the image reconstruction.
Frequency Tuning
Apart from the deep subwavelength resolution, another advantage of our designed graphene superlens is that it can be easily tuned to work over a broadband frequency range. As we have pointed out, what dominates the edge modes propagation on the graphene sheet is σg1, hence, it must be accurately controlled. But there is a wide range of values for σg2 to insure the Fresnel reflection of surface wave. A typical value range of Im(σg2) can be −0.5 mS ~ 0.01 mS. Therefore, the performance of the superlens is not sensitive to σg2. We only need to modulate the value of σg1 for frequency tuning. This is totally different from those hyperbolic-dispersion-based super-resolution imaging mechanisms which need to accurately control σg1 and σg2 simultaneously29,41. Actually, if we do not take into account the difficulty of preparing the graphene nanoribbon samples and adding the voltage gates on each of the ribbons, we can also use the model in Fig. 1(b) to realize frequency tuning.
As mentioned above, the principle of realizing super-resolution imaging is to set up the Fabry-Perot resonance. To ensure this, we only need to adjust the gate voltage to get a identical qep at different working frequency when lg is fixed. To achieve this, uc must follow a linear relation with the square of f, i.e. uc = α·f2, in which α is a positive constant, known from equation (2). When the working frequency is tuned from 4.3 THz to 9 THz, the calculated uc must increase from 0.111 eV to 0.486 eV accordingly, as shown in Fig. 4(a). The corresponding conductivity of the graphene is from 0.0356 + i0.481 mS to 0.0357 + i1.01 mS. The upper limit of the frequency range is a conservative estimation. If high quality graphene with large carrier density (could be achieved by highly doping) is available, a higher working frequency can be expected.
(a) is the color map of the imaginary part of the conductivity as a function of f and uc. The width of the ribbons is d = 0.2 μm. The white dashed line in the figure illustrates the frequency tuning path, ranged from 4.3 THz~9 THz. (b) presents the theoretical (solid line) and simulated (square dots) losses as a function of the tuning frequency. The losses are characterized by the propagation length of the edge mode. (c) is the normalized image as a function of the tuning frequency. The image curves at the low (4.4 THz) and high (8.8 THz) spectral window are presented in the inset.
The lower limit of the frequency range is mainly subjected to the losses. The losses can be characterized by the propagation length of the edge mode, which should refer to the imaginary part of the wave-vector. In the working frequency range, the propagation length can be roughly calculated by L = [Im(qp)]−1. As shown in Fig. 4(b), the propagation length increases from 5.48 μm to 11.66 μm if we tune the frequency from 4.3 THz up to 9 THz. The square dots are the simulated results of the 200 nm nanoribbon. The theoretical and simulated results are in good agreement. The losses decrease when the frequency increases. The minimum propagation length is much larger than the length of the nanoribbons. In Fig. 4(c), we plot the color mapping of the normalized images of two sources as a function of frequency. The two sources are separated by 800 nm. The images are detected along a x-direction line which is 60 nm away from the emergence interface. From 4.3 THz to 9 THz, the two peaks corresponding to the two targets can always be distinguished. The image curves at the low (4.4 THz) and the high (8.8 THz) spectral window are also presented in the inset of Fig. 4(c). The two peaks in the two curves are still obvious although the qualities of the images are slightly deteriorative.
Magnifying subwavelength targets
In practical applications, we always hope magnified images could be obtained so that two objects could be distinguished by conventional imaging system. Hyperlenses which allow magnification of deep subwavelength scale objects have been proposed by using anisotropic materials with hyperbolic dispersions14. Our further study finds that, the goal can be realized by shaping the grating metallic gate into radial pattern, as shown in Fig. 5(a). By doing this, graphene ribbons with gradual increased width can be built, where r1 and r2 are respectively the inner and the outer radius of the ribbons, θ is the angle of the ribbon. The basic principle is the same as above. But in this case, the plasmon wavelength of edge mode is no longer constant at a given frequency because the width of each ribbon is gradually broadening. Hence, the Fabry-Perot resonance condition now becomes
(a) is the schematic of the superlens. The voltage gate is a fan-shaped metallic grating. (b) is the simulated electric fields mapping at the z = 60 nm plane for the cases of r2 = 3.2 μm and 4.88 μm. (d) is the electric field mapping at z = 200 nm plane, corresponding to the case r2 = 4.88 μm. The sources and the 2D images at the output curved plane are shown in (e). (f) presents the simulation corresponding to (d) but with loss being considered. The two line sources are separated by 0.8 μm.

in which, lg = r2 - r1. When the working frequency is 8 THz, the conductivities of the graphene ribbons become σg1 = 0.0357 + i0.898 mS and σg2 = 2.38×10−4 + i5.98×10−3 mS. The magnification factor of image can be calculated by γ = r2/r1. If r1 is fixed, increasing the value of r2 would enlarge the magnification factor. Nevertheless, the value of r2 can only be discrete because the Fabry-Perot resonance condition must be fulfilled. To prove it, we choose r1 = 0.8 μm, θ = 8°. The duty ratio of the gate is 0.5. Two surface sources separated by 800 nm are located 60 nm away from the incoming interface. The simulated electric field mapping at the z = 10 nm plane for the cases of r2 = 3.2 μm and 4.88 μm are respectively shown in Fig. 5(b,c). As we can note, the two targets are resolved and gradually magnified with the help of the edge modes. In Fig. 5(d), the electric field mapping at z = 200 nm plane is also presented. Because of the evanescent decay of the fields in the z direction, the strongly confined edge modes become 2D “bulk” modes. As shown in Fig. 5(e), the space of the two sources is respectively magnified by 4 folds and 6.1 folds in the two cases.
The lossless simulations have perfectly demonstrated the mechanism of realizing magnified super-resolution imaging. But in reality, the compromise should be made between the loss and the magnification factor. As we can see in Fig. 5(f), when the loss is considered in Fig. 5(d), the performance of the superlens is influenced but still competent for targets recognition.
Realizing far-field super-resolution imaging requires a relative long graphene ribbon (≈40 μm). Although in our demonstrations, the length (corresponding to the magnification factor) is not sufficient for compressing the evanescent spatial spectrum of the deep subwavelength targets into propagating spectrum, far-field super resolution imaging could also be predicted if we lower the designed maximum resolution (correspondingly, reduce the required length of ribbons) or mitigate the loss influence. The method of realizing frequency tuning for this superlens is the same as above, therefore, we will not cover it again.
In reality, the boundaries between the high and low carrier density regions cannot be made infinitely sharp electrostatically. To discuss the influence, four conductivity profiles are considered, as shown in Fig. 6(a). The first one is the perfect rectangular profile, i.e. the profile we used above. The fourth one fulfills the standard cosine function, which can be expressed by  , we imagine this is the worst case. The conductivity profile of the second and third ones can be expressed by
, we imagine this is the worst case. The conductivity profile of the second and third ones can be expressed by

with the γ respectively being γ2 = 0.2 and γ3 = 0.5. We find that, decreasing γ means the profile is closer to the perfect one. The simulated results of the four cases are shown in Fig. 6(b). Even though the conductivity profile is not infinitely sharp, the edge plasmons are also excited. However, the wavelength of the edge mode slowly increases with the conductivity profile getting close to be worse. This is reasonable because the conductivities near the boundaries change with the profile. The increasing of the edge mode wavelength caused by the non-ideal boundaries would introduce error when calculating the Fabry-Perot resonance condition. But the mechanism of near-field super-resolution imaging still holds. Hence, the practical length of the graphene ribbons must be adjusted according to the fabricating error.
The structure of our proposed graphene superlens is simple, losses in the superlens mainly comes from the graphene material. Generally speaking, the losses of graphene is related to the temperature, the electron relaxation time, the chemical potential and the working frequency. The imaging mechanism can be extended to a broadband frequency range (up to infrared). Even though the demonstrated propagation lengths of the edge plasmon modes are limited, the lengths could be further increased by optimzing the parameters of the graphene and the frequency to reduce loss. We believe it is possible for using the graphene superlens in practical applications.
To conclude, we have introduced a new way to realize deep super-resolution imaging in the THz frequency range by using a monolayer graphene sheet tuned by a grating voltage gate. Magnified images of subwavelength targets also can be obtained by shaping the voltage gate. The finest resolution of the superlenses can reach 400 nm. Furthermore, the superlenses can be tuned to work over 4.3 THz ~ 9 THz frequency range. Owing to the strong confinement of the graphene plasmon edge mode, the images are well resolved in both the x and the z directions. It indicates that our proposal may be suitable for 2D super-resolution imaging. The mechanism could be extended to the infrared frequency range. The proposal could find potential applications in THz near-field imaging systems.
Methods
Numerical simulations are performed by the commercial software, Comsol Multiphysics, which is based on the Finite Element Method (FEM). The direct and iterative solvers are employed. The monolayer graphene sheet or ribbon is characterized by surface currents j∥ = σgE∥, where the symbol “∥” means the component is parallel to the surface of the graphene. According to the Kubo formula, the two specific intraband and interband electron transitions contribute to the surface conductivity of a monolayer graphene, which can be calculated from42

in which, e is the electron charge, ħ and kB are the Plank’s constant and the Boltzman’s constant, respectively. The chemical potential depends on the carrier density ns which is controlled by the gate voltage. Notice that for relatively small frequencies(ħω/μc ≪ 1), the intraband electron transition dominates the conductivity, hence, In the condition of μc ≫ kBT, a simple semiclassical model for conductivity, which possesses a Drude-like expression, is obtained

The imaging targets in the simulating models are two rectangular surfaces. The width and the length of the two surfaces are 250 nm and 500 nm, respectively. The excitation sources are surface currents added on both of the two rectangular surfaces. The direction of the currents is perpendicular to the graphene. The minimum size of the grid is smaller than 1/6 of the plasmon wavelength.
Additional Information
How to cite this article: Tang, H.-H. et al. Tunable Terahertz Deep Subwavelength Imaging Based on a Graphene Monolayer. Sci. Rep. 7, 46283; doi: 10.1038/srep46283 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
P. U. Jepsen, D. G. Cooke & M. Koch . Terahertz spectroscopy and imaging–Modern techniques and applications. Laser & Photonics Rev. 5, 124–166 (2011).
M. Tonouchi . Cutting-edge terahertz technology. Nat. photonics 1, 97–105 (2007).
W. L. Chan, J. Deibel & D. M. Mittleman . Imaging with terahertz radiation. Rep. Prog. Phys. 70, 1325(2007).
J. B. Pendry . Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966 (2000).
O. Mitrofanov, I. Brener, T. S. Luk & J. L. Reno . Photoconductive terahertz near-field detector with a hybrid nanoantenna array cavity. ACS. Photonics. 2, 1763–1768 (2015).
A. J. Huber, F. Keilmann, J. Wittborn, J. Aizpurua & R. Hillenbrand . Terahertz near-field nanoscopy of mobile carriers in single semiconductor nanodevices. Nano. Lett. 8, 3766–3770 (2008).
A. Doi, F. Blanchard, H. Hirori & K. Tanaka . Near-field THz imaging of free induction decay from a tyrosine crystal. Opt. Express. 18, 18419–18424 (2010).
N. Fang, H. Lee, C. Sun & X. Zhang . Sub-diffraction-limited optical imaging with a silver superlens. Science 308, 534–537 (2005).
K. J. Webb & M. Yang . Subwavelength imaging with a multilayer silver film structure. Opt. Lett. 31, 2130–2132 (2006).
T. Taubner, D. Korobkin, Y. Urzhumov, G. Shvets & R. Hillenbrand . Near-field microscopy through a SiC superlens. Science 313, 1595 (2006).
W. L. Barnes, A. Dereux & T. W. Ebbesen . Surface plasmon subwavelength optics. Nature 424, 824–830 (2003).
K. Wang & D. M. Mittleman . Metal wires for terahertz wave guiding. Nature 432, 376–379 (2004).
I. Smolyaninov, Y.-J. Hung & C. C. Davis . Magnifying superlens in the visible frequency range. Science 315, 1699–1701 (2007).
Z. Liu, H. Lee, Y. Xiong, C. Sun & X. Zhang . Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 315, 1686 (2007).
E. Pickwell & V. P. Wallace . Biomedical applications of terahertz technology. J. Phys. D: Appl. Phys. 39, R301 (2006).
K. Kawase, Y. Ogawa, Y. Watanabe & H. Inoue . Non-destructive terahertz imaging of illicit drugs using spectral fingerprints. Opt. Express 11, 2549–2554 (2003).
J. B. Pendry, L. Martin-Moreno & F. J. Garcia-Vidal . Mimicking surface plasmons with structured surfaces. Science 35, 847–848 (2004).
H.-H. Tang, T.-J. Ma & P.-K. Liu . Experimental demonstration of ultra-wideband and high-efficiency terahertz spoof surface plasmon polaritons coupler. Appl. Phys. Lett. 108, 191903 (2016).
H.-H. Tang & P.-K. Liu . Terahertz far-field superresolution imaging through spoof surface plasmons illumination. Opt. Lett. 40, 5822–5825 (2015).
S. A. Maier, S. R. Andrews, L. Martin-Moreno & F. J. Garcia-Vidal . Terahertz surface Plasmon-polariton propagation and focusing on periodically corrugated metal wires. Phys. Rev. Lett. 97, 176805 (2006).
M. Tymchenko, A. Y. Nikitin & L. Martín-Moreno . Faraday rotation due to excitation of magnetoplasmons in graphene microribbons. ACS Nano 7, 9780–9787 (2013).
T. Low & P. Avouris . Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano 8, 1086–1101 (2014).
L. Ju et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotech. 6, 630–634 (2011).
H. J. Xu, W. B. Lu, Y. Jiang & Z. G. Dong . Beam-scanning planar lens based on graphene. Appl. Phys. Lett. 100, 051903 (2012).
H. Nasari & M. S. Abrishamian . Magnetically tunable focusing in a graded index planar lens based on graphene. J. Optics 16, 105502 (2014).
P. Li, T. Wang, H. Böckmann & T. Taubner . Graphene-enhanced infrared near-field microscopy. Nano Lett. 14, 4400–4405 (2014).
P. Li & T. Taubner . Broadband subwavelength imaging using a tunable graphene-lens. ACS Nano 6, 10107–10114 (2012).
P. Wang et al. Graphene-based Superlens for Subwavelength Optical Imaging by Graphene Plasmon Resonances. Plasmonics 11, 515–522 (2016).
E. Forati, G. W. Hanson, A. B. Yakovlev & A. Alu . Planar hyperlens based on a modulated graphene monolayer. Phys. Rev. B 89, 081410 (2014).
Andryieuski, A. V. Lavrinenko & D. N. Chigrin . Graphene hyperlens for terahertz radiation. Phys. Rev. B 86, 121108 (2012).
Vakil, N. Engheta. Transformation optics using graphene. Science 332, 1291–1294 (2011).
M. Jablan, H. Buljan & M. Soljačić . Plasmonics in graphene at infrared frequencies. Phys. Rev. B 80, 245435 (2009).
E. G. Mishchenko, A. V. Shytov & P. G. Silvestrov . Guided Plasmons in Graphene p-n Junctions. Phys. Rev. Lett. 104, 156806 (2010).
Y. Nikitin, F. Guinea, F. J. García-Vidal & L. Martín-Moreno . Edge and waveguide terahertz surface plasmon modes in graphene microribbons. Phys. Rev. B. 84, 161407 (2011).
P. Berini . Plasmon-polariton waves guided by thin lossy metal films of finite width: Bound modes of symmetric structures. Phys. Rev. B. 61, 10484 (2000).
Y. Nikitin et al. Real-space mapping of tailored sheet and edge plasmons in graphene nanoresonators. Nature Photonics. 10, 239–243 (2016).
Z. Fei et al. Edge and surface plasmons in graphene nanoribbons. Nano letters. 15, 8271–8276 (2015).
J. Christensen et al. Graphene plasmon waveguiding and hybridization in individual and paired nanoribbons. ACS Nano 6, 431–440 (2011).
J. T. Shen, P. B. Catrysse & S. Fan . Mechanism for designing metallic metamaterials with a high index of refraction. Phys. Rev. Lett. 94, 197401 (2005).
L. Du, D. Tang & X. Yuan . Edge-reflection phase directed plasmonic resonances on graphene nano-structures. Opt. Express 22, 22689–22698 (2014).
B. H. Cheng, K. J. Chang, Y. C. Lan & D. P. Tsai . Actively controlled super-resolution using graphene-based structure. Opt. Express 22, 28635–28644 (2014).
G. W. Hanson . Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 103, 064302 (2008).
Acknowledgements
This work is sponsored by the National Natural Science Foundation of China under contract 61531002, 61471007.
Author information
Authors and Affiliations
Contributions
H.-H.T. and J.-Y.L. performed the simulations and demonstrated the theory with assistance from Y.T. and P.-K.L.; H.-H.T. analyzed the data with assistance from P.-K.L.; H.-H.T., T.-J.H. and P.-K.L. co-wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Tang, HH., Huang, TJ., Liu, JY. et al. Tunable Terahertz Deep Subwavelength Imaging Based on a Graphene Monolayer. Sci Rep 7, 46283 (2017). https://doi.org/10.1038/srep46283
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep46283
This article is cited by
-
THz Super-Resolution Imaging in Transmission Technology by Using Butterfly and Pattern Device Samples
Wireless Personal Communications (2023)
-
A Band Enhanced Tunable Ultra-Broadband Absorber Based on Loading the Lumped Resistors and Cavity Resonance
Plasmonics (2019)
-
Multi-functional Device with Switchable Functions of Absorption and Polarization Conversion at Terahertz Range
Nanoscale Research Letters (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.