Abstract
The coexistence of nontrivial topology and giant Rashba splitting, however, has rare been observed in two-dimensional (2D) films, limiting severely its potential applications at room temperature. Here, we through first-principles calculations to propose a series of inversion-asymmetric group-IV films, ABZ2 (A ≠ B = Si, Ge, Sn, Pb; Z = F, Cl, Br), whose stability are confirmed by phonon spectrum calculations. The analyses of electronic structures reveal that they are intrinsic 2D TIs with a bulk gap as large as 0.74 eV, except for GeSiF2, SnSiCl2, GeSiCl2 and GeSiBr2 monolayers which can transform from normal to topological phases under appropriate tensile strain of 4, 4, 5, and 4%, respectively. The nontrivial topology is identified by Z2 topological invariant together with helical edge states, as well as the berry curvature of these systems. Another prominent intriguing feature is the giant Rashba spin splitting with a magnitude reaching 0.15 eV, the largest value reported in 2D films so far. The tunability of Rashba SOC and band topology can be realized through achievable compressive/tensile strains (−4 ~ 6%). Also, the BaTe semiconductor is an ideal substrate for growing ABZ2 films without destroying their nontrivial topology.
Similar content being viewed by others
Introduction
Topological insulators (TIs) are new states of quantum matter interesting for fundamental condensed matter physics and important for practical applications1,2,3. In particular, for two-dimensional (2D) TIs, all the scatterings of conducting edge states are completely forbidden, while the surface states of three-dimensional (3D) TIs are not protected against scattering at any angles other than 180°. The helical edge states of nanoribbons made from 2D TIs provide massless relativistic carriers with intrinsic spin-momentum lock and negligible backscattering, ideal for the realization of conducting channels without dissipation in electronic devices4,5. However, quantum spin Hall (QSH) effect has only been experimentally observed in HgTe/CdTe6,7 and InAs/GaSb8,9 quantum wells at very controlled and low temperature. In spite of this successful progress, the experimental realizations of these topological quantum states in 2D films are still challengeable.
Graphene1,2, the first 2D TI model, supports an unobservable small bulk gap due to its extremely weak spin-orbit coupling (SOC). Afterwards, several candidate materials are proposed to overcome the issue in graphene for the observation of QSH effect. These samples include silicene10, germanene11, stanene12, plumbene13, bismuth14, and arsenene15, in which they exhibit the topology properties alike to grapheme, but their nontrivial bulk gaps are still small. Motivated by the experimental synthesis of hydrogenated germanene (GeH)16, the chemical functionalization on honeycomb structure, e.g., Bi/Sb/As17,18,19,20 and Ge/Sn/Pb films21,22,23,24,25,26,27, has been proposed to host QSH effect with enhanced band gaps. For example, Xu et12 reported that the nontrivial band gap of pristine stanene is merely 0.1 eV, while it is enlarged to 0.3 eV under fully halogenation12,23,24,25,26. More interestingly, the bulk gaps of 2D plumbene films with chemical decoration, PbX (X = H, F, Cl, Br and I) monolayers, have been elevated to a remarkable 1.34 eV13 the largest gap of all the reported 2D TIs as we know. All these results provide a great potential for the realization of QSH effect at room temperature in device paradigms for quantum information processing.
Rashba SOC, on the other hand, generally leads to spin-polarized band dispersion curves with in-plane opposite helical spin texture28. This feature originates from structural inversion-symmetry breaking at the surface/interface system, allowing the control of spin direction through an electric field29. As compared with inversion-symmetric TIs, these systems are called 2D inversion-asymmetric TIs (IASTIs), which are more promising due to their perfect performance in realizing new topological phenomena, such as crystalline-surface dependent topological electronic states30, pyroelectricity31, natural topological p-n junctions32 and so on. In conventional semiconductor materials33,34,35,36, Rashba SOC can only be tuned in a relatively limited range under electric field since it is generally rather weak, so it would be one of the important reasons to interpret the great attention the Datta-Das spin FET37, which still has not been realized in experiments. Recently, Arguilla et al.38 synthesize 2D honeycomb Ge1−xSnxH1−x (OH)x film from the topochemical deintercalation of CaGe2–2xSn2x. In comparison with inversion-symmetric systems15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31, the introduction of tin breaks the inversion-symmetry of 2D germanene, which may induce a significant large Rashba SOC. Motived by above suppose, we attempt to extend and advance the group-IV 2D films to realize giant Rashba SOC accompanied with nontrivial topology, which may our proposal achievable experimentally accessible.
In present work, we report on the electronic and topological properties of a series of 2D IASTIs in group-IV binary films, which are called as ABZ2 monolayers, where A and B belong to group-IV elements (Si, Ge, Sn, Pb), as well as Z is the decorated halogen atoms (F, Cl, and Br), as illustrated in Fig. 1 (a). We find that most of these group-IV binary films are demonstrated as 2D IASTIs possess sizeable band gaps, reaching a maximum value of 0.74 eV for PbSnCl2, which exceed the thermal energy at room temperature. Though GeSiF2, SnSiCl2, GeSiCl2 and GeSiBr2 monolayers are normal insulators (NI), they can transform 2D TI phases under tensile strain of 4, 4, 5, 4%, respectively. The nontrivial quantum states are identified by Z2 topological invariant together with helical edge states induced by SOC, as well as berry curvature of these systems. The most prominent feature in these systems is the giant Rashba splitting energy, for example, a value of 0.15 eV for PbSiCl2, which is the largest value reported in 2D films so far. Furthermore, a favorable tunability of Rashba SOC and nontrivial topology can be obtained through achievable compressive/tensile strains (−4 ~ 6%). We also find that the Te (111)-terminated surface in semiconductor BaTe is an ideal substrate for experimental realization of these monolayers, without destroying their nontrivial topology. The coexistence of giant Rashba SOC and band topology in these films may bring rich spin-related phenomena in 2D IASTIs, which offers a special contribution to nanoelectronics and spintronics.
Calculated methods and details
All calculations are carried out using the plane wave basis Vienna ab initio simulation pack (VASP) code39,40 implementing density functional theory (DFT). The projector-augmented wave (PAW) method41 is used to describe electron-ion potential. The exchange-correlation potential is approximated by generalized gradient approximation (GGA) in the Perdew-Burke-Ernzerhof (PBE)42 form. Considering the possible underestimation of GGA method, the Heyd-Scuseria -Ernzerhof (HSE06) hybrid functional is employed to check the band topology43. We use an energy cutoff of 450 eV and maximum residual force less than 0.001 eV/Å. Periodic boundary conditions are employed to simulate these 2D systems, and the Brillouin zone is sampled by using a 17 × 17 × 1 Gamma-centered Monkhorst-Pack grid. Moreover, SOC is taken into account in terms of the second-variational procedure. The phonon dispersion calculations are carried out by employing the PHONOPY code44 through the density-functional perturbation theory (DFPT) approach.
Results and Discussion
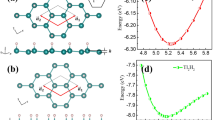
Figure 1(a) displays the honeycomb lattice of ABCl2 (A ≠ B = Si, Ge, Sn, Pb) monolayers, accompanied with its Brillouin zone in Fig. 1(b). All these configurations are iso-structural to inversion-symmetric Ge/Sn/Pb monolayers with C3v symmetry19,20,21,22,23,24,25, but the A and B sublattices are occupied with different group-IV atoms, resulting in inversion-symmetry breaking. To verify the geometric stability of these structures, the total energies ABCl2 monolayers with respect to lattice constant a are illustrated in Fig. 1(c), where a is varied to identify structural ground state. Interestingly, the double-well energy variation curves occur in all cases, namely, the high-buckled (HB) and low-buckled (LB) states, respectively. In HB structure, the vertical layer distance lies in the range of 3.58 − 5.15 Å, while the distance in LB state is smaller within 1.42−2.51 Å, as listed in Table 1. The LB structure here, however, is more stable by at least 1.04 eV per unit cell than HB structure, different form the cases of III-Bi films, where the HB structure is the ground state. Thus, we only focus on stable LB chlorinated monolayers in the following. Furthermore, the energetically structural stability is evaluated by the formation energy expressed as

Where E(ABCl2) and E(AB) are the total energies of chlorinated and pristine AB monolayers, respectively, while μ(Cl) is the chemical potential of chlorination atoms. As listed in Table 1, the calculated formation energies are in the range of −2.284 ~ −3.146 eV per atom, indicating no phase separation emerges in these systems. For practical application as a nanodevice, the 2D films should be chemically inert and environmentally friendly. Thus, the phonon spectrum dispersions are calculated and plotted in Fig. 2, which demonstrates that all ABCl2 monolayers are dynamically stable since all the vibrational models are real in the whole Brillouin zone.
The band structures of ABCl2 monolayers are shown in Fig. 3, with the orbital-projected components displayed in Fig. S1 in the Supplementary Information. In the absence of SOC, the PbSnCl2, PbGeCl2 PbSiCl2 and SnGeCl2 monolayers show gapless semiconductor feature with valence band maximum (VBM) and conduction band minimum (CBM) degenerated at the Γ point. The Fermi level locates exactly at the degenerated point with a zero density of states. Notably, the slopes of the valence band and conduction band in such a touching point show the parabolic dispersion, instead of a linear one, as illustrated by a 3D band structure for PbSnCl2 monolayer (Fig. 4 (a)). This scenario for the electronic properties is quite similar to Ge/Sn/Pb monolayers21,22,23,24,25,26,27. Upon including SOC, the band structures produce a transition from semimetal to semiconductor, as the degenerated states at the touching point separate from each other, see Figs 3(a–d) and 4(b). As observed in previously reported Bi/Sb/As17,18,19,20, the SOC-induced band-gap opening at the Fermi level is a strong indication of the existence of topologically nontrivial phases. Furthermore, from Si to Pb atom, the band gap opening gradually increases (Table 1), since the SOC effect gets stronger due to increasing atomic numbers of heavier atoms. Here we label this SOC-induced band gap at the Γ point as EΓ-soc, to be distinguished from whole gap (Eg-soc), as listed in Table 1. To eliminate the possible underestimation of the band gap, we employ additional HSE0637 to confirm the existence of band inversion for all these systems. As expected, the values of EΓ are enhanced to 0.74, 0.49, 0.41 and 0.23 eV, respectively, for PbSnCl2, PbGeCl2, PbSiCl2 and SnGeCl2 monolayers.
To confirm the nontrivial topological nature, we introduce the evolution of Wannier Center of Charges (WCCs)45 to calculate Z2 topological invariant due to inversion-symmetry breaking. The Wannier functions (WFs) related with lattice vector R can be written as:

Here, a WCCs  can be defined as the mean value of
can be defined as the mean value of  , where the
, where the  is the position operator and
is the position operator and  is the state corresponding to a WF in the cell with R = 0. Then we can obtained
is the state corresponding to a WF in the cell with R = 0. Then we can obtained

Assuming that  with S = I or II, where summation in α represents the occupied states and A is the Berry connection. So we have the format of Z2 invariant:
with S = I or II, where summation in α represents the occupied states and A is the Berry connection. So we have the format of Z2 invariant:

The Z2 invariant can be obtained by counting the even or odd number of crossings of any arbitrary horizontal reference line. Taking PbSnCl2 monolayer as an example, we present the evolution lines of WCCs in Fig. 5(a). One can see that the WCCs evolution curves cross any arbitrary reference lines odd times, yielding Z2 = 1.
(a) The evolution lines of WFC for PbSnCl2 monolayer. (b) The energy bands was calculated around the Fermi level by the method of DFT and Wannier. (c) Total (left panel) and (d) spin (right panel) edge density of states for PbSnCl2. In the spin edge plot, blue/red lines denote the spin up/down polarization.
The most important character of 2D TIs is the appearance of helical edge states with spin-polarization protected by TRS. Here we compute the edge Green’s functions using the ab initio TB model. The ab initio TB model is constructed by downfolding the bulk bands obtained by DFT calculations, using the recursive method in terms of maximally localized Wannier functions (MLWFs)46. Figure 4(c) and (d) show the orbital-decomposed band structures, in which the red and blue circles represent group-IV s and px,y states, respectively, and the symbol size is proportional to the orbital weight. Obviously, the bulk energy bands near the Fermi level are predominantly from px,y orbitals, thus the MLWFs are derived from atomic p-like orbitals. In this case, the TB bulk bands perfectly reproduce the DFT bands around the Fermi level up to ± 1.0 eV, as illustrated in Fig. 5(b). Figure 5(c) displays the local density of states (LDOS) of the calculated edge states. Indeed, all the edge bands for PbSnCl2 monolayer connect completely the conduction and valence bands and span 2D bulk gap, yielding a 1D gapless edge states, in good agreement with the Z2 invariant. By identifying spin-up and spin-down contributions in edge spectral function, the counter-propagating edge states exhibit opposite spin-polarization (Fig. 5(d)), which benefit from their robustness against nonmagnetic scattering.
For GeSiCl2 and SnSiCl2 monolayers, on the other hand, they exhibit semiconductor feature with direct band gap of 0.285 and 0.265 eV in the absence of SOC, as shown in Fig. 3(e) and (f). As we know that external strain is an effective avenue to tune the band gap, this may introduce a band inversion by SOC. To simulate strain effects on the electronic structures, we employ the external strain to these systems which is defined as ε = (a-a0)/a0, where a and a0 are lattice constants with and without strains, respectively. In Fig. 6 we present the band structures with respect to external strains of GeSiCl2 as an example, where the red and blue colors represent s and px,y states, respectively. One can see that the band structure of GeSiCl2 is sensitive to the lattice expansion. Without SOC, the CBM (s) and VBM (px,y) move toward each other, leading to a reduction of band gap. The band gap closes at the Γ point when ε = 5%, as illustrated in Fig. 6(c), suggesting semi-metallic character at the Fermi level. When the tensile strains are beyond 5%, the px,y orbitals shifted above s orbital, see Fig. 6(d). As a consequence, the opposite spatial shift of VBM and CBM decreases the band gap, which is essential to topological phase transitions. With increasing biaxial strain, the energy difference (Es-p) between the s and px,y orbitals at the Γ point near the Fermi level increase monotonically, but the system remains the semi-metallic feature. When SOC is included, a sizable band gap opens, see Fig. 6(e–h). Similar results are also found in SnSiCl2 monolayer in Fig. 7, but its critical point of elastic strain is 4%, smaller than GeSiCl2 monolayer. Such an SOC-induced band gap reopening usually corresponds to a NI - TI transition, as illustrated in Fig. 8.
To gain a physical understanding of QSH effect, we analyze the orbital contribution around the Fermi level for GeSiCl2 monolayer. Figure 9 presents the band evolution at the Γ point, in which the energy levels near the Fermi level are mainly composed of s and px,y orbitals from group-IV elements. The chemical bonding between Si-Ge atoms makes it split into the bonding and antibonding states, i.e., s± and px,y±, respectively. At ground state in Fig. 9(a), the bands near the Fermi level are contributed by the px,y+ and s−, with the s− being above px,y+, indicating a normal band order. When considering the external tensile strains, as illustrated in Fig. 9(b), the enlarged lattice constant weakens the interactions between A and B sublattices, decreasing the splitting between the bonding and antibonding states, which lowers s− and raises px,y+ level accordingly. Thus, depending on the strength of interatomic coupling, the band gap of GeSiCl2 can be continuously reduced, with the band order being reversed at critical point (ε = 5%), making it a 2D TI with Z2 = 1. In another words, the level crossing leads to a parity exchange between occupied and unoccupied bands, inducing a NI-TI phase transition. While for PbSnCl2, PbGeCl2 PbSiCl2 and SnGeCl2 monolayers, the lattice constant (See Fig. 1(c) and Table 1) is enlarged significantly at equilibrium state, equal to strain-induced GeSiCl2, thus they are native 2D TIs without any strain. Herein, we must point out that, although the s-px,y band inversion is caused mainly by the strength of interatomic coupling, the SOC is still indispensable because it makes the px,y+ orbital split into p+x+iy,↑& p+x-iy,↓ and p+x-iy,↑& p+x+iy,↓, opening a larger band gap. In previous works, the topological feature mainly originates from pz states such as graphene and silicene1,2,3, but here the band topology is attributed to the contribution of px,y orbitals on group-IV elements, thus their band gap is enhanced significantly.
Furthermore, to clearly show the QSH effect in these systems and confirm its nontrivial topology, we also calculate the intrinsic spin Hall conductivity of PbSnCl2 monolayer. Using the Kubo formula47,48, the spin Hall conductivity tensor is expressed as,

Here the spin Berry curvature is given by

where n is the band index, ψn,k is the eigenstate, vy is the velocity operator, and jx is the spin current operator defined as (szvx + vxsz)/2. Also, a factor of 2e/ћ in σSH is multiplied to convert its unit into the conventional electron conductivity e2/h. Figure 10(a) displays the k-resolved spin Berry curvature at the Fermi level. One can clearly see the positive peak of ΩSH(k) around the Γ point, which is consistent with its band topology. The spin Hall conductance via its chemical potential shows a nearly quantized value 2e2/h of conductance within the energy window of the SOC gap ranging from about − 0.2 eV to the Fermi energy, demonstrating that the QSH effect could be easily observed experimentally at room temperature.
(a) The k-resolved spin Berry curvature at the Fermi level of PbSnCl2 monolayer. (b) The Rashba splitting energy ER and the momentum offset kR of PbSiCl2 monolayer. (c) Spin texture in the highest valence bands for PbSnCl2 monolayer. Arrows refer to the in-plane orientation of spin, and the color background denotes the z component of the spin. (d) The energy band for ABF2, ABBr2 (A≠B = Si, Ge, Sn, Pb) systems.
The most prominent feature in inversion-asymmetric systems is the existence of giant Rashba SOC in valence band edge rather than Dresselhaus splitting49. These can be confirmed by the spin texture of Rashba spin splitting in Fig. 10(c), in which the spins of the electronic states  are oppositely aligned within the kx and ky plane, and are normal to the wave vector k. Here, we magnify the Rashba splitting energy ER and the momentum offset kR in Fig. 10(b), which corresponds to the splitting of the VBM along momentum direction at the Γ point, indicated by the rectangular box in Fig. 3(c). According to the linear Rashba model of the 2D systems, the dispersion of Rashba splitting can be expressed as
are oppositely aligned within the kx and ky plane, and are normal to the wave vector k. Here, we magnify the Rashba splitting energy ER and the momentum offset kR in Fig. 10(b), which corresponds to the splitting of the VBM along momentum direction at the Γ point, indicated by the rectangular box in Fig. 3(c). According to the linear Rashba model of the 2D systems, the dispersion of Rashba splitting can be expressed as  with k = (kx, ky), where the m* is effective mass and
with k = (kx, ky), where the m* is effective mass and  is the Rashba constant. Thus we can obtain a giant Rashba parameter eV/Å than the well-known oxide interface LaAlO3/SrTiO3 (0.01–0.05 eV/Å)50,51,52, quantum well InGaAs/InAlAs (0.07 eV/Å)53 and Au (111) surface54. These great Rashba splitting energy ER and momentum offset kR are desired for stabilizing spin and achieving a significant phase offset for different spin channels.
is the Rashba constant. Thus we can obtain a giant Rashba parameter eV/Å than the well-known oxide interface LaAlO3/SrTiO3 (0.01–0.05 eV/Å)50,51,52, quantum well InGaAs/InAlAs (0.07 eV/Å)53 and Au (111) surface54. These great Rashba splitting energy ER and momentum offset kR are desired for stabilizing spin and achieving a significant phase offset for different spin channels.
It is noteworthy that strain engineering can not only tune the topological phase, but also change the Rashba spin splitting significantly in these monolayers. In Fig. 11, we present three parameters (ER, kR, αR) under different biaxial strains by solid triangles for PbSiCl2 as an example. These three parameters decrease monotonically with the increasing lattice constants, demonstrating that a compressive/tensile strain can enhance/decrease the Rashba SOC strength. For example, the Rashba splitting can reach up to 0.182 eV under −4% strain. Thus, by biaxial strain engineering, we can enhance or reduce the SOC strength according to the experimental demands. The Rashba spin splitting of energy bands obtained here provides a chance for spintronic device applications without magnetic field, for instance, spin field-effect transistor (FET).
Finally, we must point out that that the chlorination in group-IV monolayers is not the only way to achieve QSH effect, the same results can be obtained by decorating the surface with other halogens, such as F and Br atoms. As evidenced in Fig. S2 in the supplementary information, the double-well energy curve still exists, with the LB structure being a ground state. The corresponding band structures of ABF2 and ABBr2 monolayers with and without SOC are further plotted in Fig. 12. Most of halogenated ABX2 monolayers are similar to chlorinated ones with a topological invariant Z2 = 1, except for GeSiF2 and GeSiBr2 with Z2 = 0. However, they can transform into QSH insulators under external strain of 4%, as illustrated in Fig. 8(a) and (c). In addition, Fig. 8 presents the calculated band gaps at equilibrium states, accompanied with the lattice parameters listed in Tables SI and II. Interestingly, the nontrivial band gaps can reach as large as 0.11–0.63 eV (Fig. 10(d)), which is comparable or larger than stanene (0.1 eV)12 or bismuth (0.2 eV)14. Such large nontrivial band gaps are capable of stabilizing the boundary current against the influence of thermally activated bulk carriers, and thus are beneficial for high-temperature applications.
Experimentally, choosing a suitable substrate is a key factor in device application, since a free-standing film must be eventually deposited or grown on a substrate. Considering the small lattice constant mismatch between PbSnCl2 and semiconductor BaTe55, we select Te-terminated (111) surface of semiconductor BaTe to support PbSnCl2 monolayer, as illustrated in Fig. 13. In the equilibrium state, the bottom (top) Sn atoms in PbSnCl2 are located at top (hcp) sites of the substrate, while the top Pb atoms are located at hcp sites, see Fig. 13(a) and (b). On this Te-terminated surface, Sn atoms bind preferably on top of Te atoms by forming chemical bonds, so the pz orbital of group-IV atoms and dangling bond of the substrate are both fully passivated. Figure 13(c–f) present the band structures with and without SOC, respectively. One can see that a few bands appear within the bulk gap of substrate around the Fermi level, which is mostly contributed by group-IV atoms according to wave-function analysis. By projecting Bloch wave functions onto atomic orbitals of PnSnCl2, Bloch states contributed by the s orbital of group-IV atoms are visualize by red dots. These states shift to valence bands around the Γ point, suggesting a clear s-p band order. This SOC-induced band gap is topologically nontrivial as explained by the band inversion, thus it is a robust 2D TI on Te-terminated substrate of BaTe semiconductor.
Conclusions
In summary, by means of first-principles calculations, we predict a series of inversion-asymmetric group-IV monolayers, ABZ2 (A≠B = Si, Ge, Sn, Pb; Z = F, Cl, Br), allows for the simultaneous presence of topological order and Rashba SOC. The phonon spectrum calculations reveal that they are dynamically stable. The analyses of electronic structures reveal that most of these monolayers are native 2D TIs with a bulk gap as large as 0.74 eV, while GeSiF2, SnSiCl2, GeSiCl2 and GeSiBr2 can transform from normal to topological phases under tensile strain of 4, 4, 5 and 4%, respectively. The nontrivial topology is identified by Z2 topological invariant together with helical edge states, as well as the berry curvature of these systems. The most intriguing feature is their giant Rashba spin splitting with a magnitude reaching 0.15 eV for PbSiCl2, the largest value reported in 2D films so far. A large tunability of Rashba SOC and band topology can be realized through achievable compressive/tensile strains (−4 ~ 6%). In addition, the Te(111)-terminated surface in semiconductor BaTe is predicted to be an ideal substrate for experimental realization of these systems, without destroying their nontrivial topology. Considering their simple crystal structure as well as large nontrivial band gap and giant Rashba splitting energy in these monolayers, these findings present a platform to explore 2D inversion-asymmetric TIs for room-temperature device applications.
Additional Information
How to cite this article: Zhang, S.- et al. Two-Dimensional Large Gap Topological Insulators with Tunable Rashba Spin-Orbit Coupling in Group-IV films. Sci. Rep. 7, 45923; doi: 10.1038/srep45923 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in grapheme. Phys. Rev. Lett. 95, 226801 (2005).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Moore, J. E. Majorana’s wires. Nature Nanotech 8, 194–198 (2013).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature (London) 460, 1101 (2009).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Bernevig, B. A. et al. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757 (2006).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells, Science 318, 766 (2007).
Du, L. et al. Robust helical edge transport in gated InAs/GaSb bilayers. Phys. Rev. Lett. 114, 096802 (2015).
Liu, C. et al. Quantum spin Hall effect in inverted type-II semiconductors. Phys. Rev. Lett. 100, 236601 (2008).
Zhang, R. W. et al. Silicon-based Chalcogenide: Unexpected Quantum Spin Hall Insulator with Sizable Band Gap. Appl. Phys. Lett. 109, 182109 (2016).
Liu, C. C. et al. Quantum spin Hall effect in silicene and two-dimensional germanium. Phys. Rev. Lett. 107, 076802 (2011).
Xu, Y. et al. Large-gap quantum spin Hall insulators in tin films. Phys. Rev. Lett. 111, 136804 (2013).
Zhao, H. et al. Unexpected Giant-Gap Quantum Spin Hall Insulator in Chemically Decorated Plumbene Monolayer. Sci. Rep. 6, 20152 (2016).
Wada, M. et al. Localized edge states in two-dimensional topological insulators: Ultrathin Bi films. Phys. Rev. B 83, 121310 (2011).
Wang, Y. P. et al. Tunable quantum spin Hall effect via strain in two-dimensional arsenene monolayer. J. Phys. D: Appl. Phys. 49, 055305 (2016).
Bianco, E. et al. Stability and exfoliation of germanane: a germanium graphane analogue. ACS Nano 7, 4414 (2013).
Ma, Y. D. et al. Robust two-dimensional topological insulators in methyl-functionalized bismuth, antimony, and lead bilayer films. Nano Lett. 15, 1083 (2015).
Zhou, M. et al. Epitaxial growth of large-gap quantum spin Hall insulator on semiconductor surface. PNAS 111, 14378 (2014).
Song, Z. G. et al. Quantum Spin Hall and Quantum Valley Hall Insulators of BiX/SbX (X = H, F, Cl, and Br) Monolayer with a Record Bulk Band Gap, NPG Asia Mater. 6, e147 (2014).
Wang, Y. P. et al. Controllable band structure and topological phase transition in two-dimensional hydrogenated arsenene. Sci. Rep. 6, 20342 (2016).
Si, C. et al. Functionalized germanene as a prototype of large-gap two-dimensional topological insulators. Phys. Rev. B 89, 115429 (2014).
Xu, Y. et al. Large-gap quantum spin Hall states in decorated stanene grown on a substrate. Phys. Rev. B 92(8), 081112 (2015).
Zhang, R. W. et al. Ethynyl-functionalized stanene film: a promising candidate as large-gap quantum spin Hall insulator. New. J. Phys. 17, 083036 (2015).
Zhang, R. W. et al. Room Temperature Quantum Spin Hall Insulator in Ethynyl-Derivative Functionalized Stanene Films. Sci. Rep. 6, 18879 (2016).
Wang, Y. P. et al. Large-gap quantum spin Hall state in functionalized dumbbell stanene, Appl. Phys. Lett. 108, 073104 (2016).
Zhang, R. W. et al. New family of room temperature quantum spin Hall insulators in two-dimensional germanene film. J. Mater. Chem. C 4, 2088 (2016).
Zhao, H. et al. First-principles prediction of a giant-gap quantum spin Hall insulator in Pb thin film, Phys. Chem. Chem. Phys. 18, 31862 (2016).
Bychkov, Y. A. & Rashba, E. I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 39, 78 (1984).
Jia, Y. Z. et al. First-Principles Prediction of Inversion-Asymmetric Topological Insulator in Hexagonal BiPbH Monolayer. J. Mater. Chem. C 4, 2243 (2016).
Bahramy, M. S. et al. Emergence of non-centrosymmetric topological insulating phase in BiTeI under pressure. Nat. Commun. 3, 679 (2012).
Wan, X. et al. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Wang, J. et al. Topological p-n junction, Phys. Rev. B 85, 235131 (2012).
Zhong, Z. et al. Theory of spin-orbit coupling at LaAlO 3/SrTiO 3 interfaces and SrTiO 3 surfaces. Phys. Rev. B 87, 161102 (2013).
Nitta, J. et al. Gate Control of Spin-Orbit Interaction in an Inverted In 0.53 Ga 0.47 As/In 0.52 A l0.48 As Heterostructure. Phys. Rev. Lett. 78, 1335 (1997).
Lashell, S. et al. Spin splitting of an Au (111) surface state band observed with angle resolved photoelectron spectroscopy. Phys. Rev. Lett. 77, 3419 (1996).
Tesch, U. et al. Structural and electronic properties of graphene nanoflakes on Au (111) and Ag (111). Sci. Rep. 6, 23439 (2016).
Datta, S. & Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 56, 665 (1990).
Arguilla, M. Q. et al. Goldberger, Synthesis and stability of two-dimensional Ge/Sn graphane alloys. Chem. Mater. 26, 6941–6946 (2014).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Fisher, A. J. et al. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Perdew, J. P. et al. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Heyd, J. & Scuseria, G. E. Ernzerhof M. Erratum: “Hybrid functionals based on a screened Coulomb potential”. J. Chem. Phys. 124, 219906 (2006).
Togo, A. et al. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Yu, R., Qi, X. L., Bernevig, A., Fang, Z. & Dai, X. Phys. Rev. B 84, 075119 (2011).
Klimeš, J., Bowler, D. R. & Michaelides, A. Phys. Rev. B 83, 195131 (2011).
Yao, Y. G. & Fang, Z. Sign changes of intrinsic spin Hall effect in semiconductors and simple metals: first-principles calculations. Phys. Rev. Lett. 95, 156601 (2005).
Guo, G. Y. et al. Ab initio calculation of the intrinsic spin Hall effect in semiconductors. Phys. Rev. Lett. 94, 226601 (2005).
Rashba, I. E. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 2, 1109 (1960).
Caviglia, A. D. et al. Tunable Rashba spin-orbit interaction at oxide interfaces. Phys. Rev. Lett. 104, 126803 (2010).
Fête, A. et al. Rashba induced magnetoconductance oscillations in the LaAlO3-SrTiO3 heterostructure. Phys. Rev. B 86, 201105 (2012).
Zhong, Z. et al. Theory of spin-orbit coupling at LaAlO 3/SrTiO 3 interfaces and SrTiO3 surfaces. Phys. Rev. B 87, 161102 (2013).
Nitta, J. et al. Gate Control of Spin-Orbit Interaction in an Inverted In 0.53 Ga 0.47 As/In 0.52 A l0.48 As Heterostructure. Phys. Rev. Lett. 78, 1335 (1997).
Lashell, S. et al. Spin splitting of an Au (111) surface state band observed with angle resolved photoelectron spectroscopy. Phys. Rev. Lett. 77, 3419 (1996).
Miller, E. et al. The Preparation and Properties of Barium, Barium Telluride, and Barium Selenide. Trans. Metall. Soc. AIME 218, 978 (1990).
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant Nos. 11434006 and 11304121).
Author information
Authors and Affiliations
Contributions
S. Z and C. Z conceived the study and wrote the manuscript. W. J performed the first-principles calculations and calculated the phonon spectrum. P. L and P. W. prepared figures. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, Sj., Ji, Wx., Zhang, Cw. et al. Two-Dimensional Large Gap Topological Insulators with Tunable Rashba Spin-Orbit Coupling in Group-IV films. Sci Rep 7, 45923 (2017). https://doi.org/10.1038/srep45923
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep45923
This article is cited by
-
Defect-mediated Rashba engineering for optimizing electrical transport in thermoelectric BiTeI
npj Computational Materials (2020)
-
Stanene-hexagonal boron nitride heterobilayer: Structure and characterization of electronic property
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.