Abstract
We show a new resonance acceleration scheme for generating ultradense relativistic electron bunches in helical motions and hence emitting brilliant vortical γ-ray pulses in the quantum electrodynamic (QED) regime of circularly-polarized (CP) laser-plasma interactions. Here the combined effects of the radiation reaction recoil force and the self-generated magnetic fields result in not only trapping of a great amount of electrons in laser-produced plasma channel, but also significant broadening of the resonance bandwidth between laser frequency and that of electron betatron oscillation in the channel, which eventually leads to formation of the ultradense electron bunch under resonant helical motion in CP laser fields. Three-dimensional PIC simulations show that a brilliant γ-ray pulse with unprecedented power of 6.7 PW and peak brightness of 1025 photons/s/mm2 /mrad2 /0.1% BW (at 15 MeV) is emitted at laser intensity of 1.9 × 1023 W/cm2.
Similar content being viewed by others
Introduction
γ-ray is an electromagnetic radiation with extremely high frequency and high photon energy. As a promising radiation source, it has a broad range of applications in material science, nuclear physics, antimatter physics1,2,3, logistics for providing shipment security, medicine4 for sterilizing medical equipment and for treating some forms of cancer, e.g. gamma-knife surgery5. γ-ray from distant space can also provide insights into many astrophysical6,7 phenomena, including γ-ray bursts, cosmic ray acceleration at shock wave front, and emission from pulsar.
Generating intense bursts of high-energy radiation usually requires the construction of large and expensive particle accelerators8,9. Laser-driven accelerators offer a cheaper and smaller alternative, and they are now capable of generating bursts of γ-rays10. γ-ray generation has been demonstrated in a number of experiments on laser interactions with solid and gas targets, where the main mechanism is the Bremsstrahlung radiation of fast electrons interacting with high-Z material targets11,12,13,14,15,16,17. However, due to the small bremsstrahlung cross-section, the conversion efficiency of this scheme is rather low. Further, the broad divergence and large size of fast electron source also limit the achievable brightness of the generated γ-rays. γ-ray can also be produced by the nonlinear Compton backscattering, in which an electron beam accelerated by laser wakefields interacts with a counterpropagating laser pulse18,19,20,21,22. However, the number of electrons accelerated by laser wakefields in underdense plasmas is small, which also leads to rather low peak brightness of the produced γ-rays. Recent experiment17 demonstrates that the peak brightness of the γ-ray pulse at 15 MeV can reach only the order of 1020 photons/s/mm2/mrad2/0.1% BW.
With the progress of laser technology, laser intensities of 5 × 1022 W/cm2 are now available23 and are expected to reach the order of 1023–1024 W/cm2 in the next few years24, where the quantum electrodynamic (QED) effects play role in their interaction with plasmas. In the QED laser-plasma interaction regime, a promising mechanism for production of γ-ray photons is the nonlinear synchrotron radiation25,26,27,28,29,31 of ultrarelativistic electrons in the laser fields, i.e.,  30. It is shown that γ-ray photons with the maximum energy extending to 100 s MeV can be generated by irradiating a solid target with an ultraintense laser26,27,28. However, for laser interaction with steep solid density targets, where no preplasmas exist, the γ-ray emission occurs only in the small skin-depth region2,26,27,28, therefore, the conversion efficiency from laser to γ-rays is still low, and the peak brightness of γ-rays is also limited. Recently, a self-matching resonance acceleration scheme32,33 in near-critical plasmas by circularly polarized laser pulses has been explored, which can generate much denser relativistic electron beams than the case of direct laser acceleration with linearly polarized lasers34,35. However, the laser intensity used there is comparatively low in the non-QED regime, electron resonance acceleration is dominantly governed by only the self-generated electromagnetic fields in the plasma, which limits both the energy and the density of the electron bunch for synchrotron radiation.
30. It is shown that γ-ray photons with the maximum energy extending to 100 s MeV can be generated by irradiating a solid target with an ultraintense laser26,27,28. However, for laser interaction with steep solid density targets, where no preplasmas exist, the γ-ray emission occurs only in the small skin-depth region2,26,27,28, therefore, the conversion efficiency from laser to γ-rays is still low, and the peak brightness of γ-rays is also limited. Recently, a self-matching resonance acceleration scheme32,33 in near-critical plasmas by circularly polarized laser pulses has been explored, which can generate much denser relativistic electron beams than the case of direct laser acceleration with linearly polarized lasers34,35. However, the laser intensity used there is comparatively low in the non-QED regime, electron resonance acceleration is dominantly governed by only the self-generated electromagnetic fields in the plasma, which limits both the energy and the density of the electron bunch for synchrotron radiation.
In this paper, by using a near-critical plasma interaction with ultraintense circularly polarized (CP) laser pulses, we report on a new resonance acceleration scheme in the QED regime for generating ultradense ultrarelativistic electron bunches in helical motions [see Fig. 1(a)] and therefore emitting brilliant vortical γ-ray pulses. In this QED scheme, on the one hand, because of the quantum radiation losses, the transverse phase space of electrons is confined36,31, and the electrons are easily trapped in the center of laser-produced plasma channel; on the other hand, due to the additional contribution of radiation reaction recoil force, the resonance bandwidth37 between laser frequency (in the electron rest frame) and that of electron betatron oscillation under quasistatic electromagnetic fields in the channel is significantly broadened, that is, the resonance condition is much relaxed. Both of these effects result in formation of an ultradense electron bunch under resonant helical acceleration in CP laser fields, where both the particle number and energy are much larger than those under only direct laser acceleration (DLA) by linearly polarized lasers29,31. Furthermore, the synchrotron radiation efficiency is much enhanced by the resonant electrons’ helical motion feature in the self-generated axial and azimuthal magnetic fields due to the use of CP lasers, comparing with that by linearly polarized lasers29,31, eventually leading to production of brilliant petawatt vortical γ-ray pulses. Three dimensional (3D) particle-in-cell (PIC) simulations show that brilliant γ-ray pulses with unprecedented peak brightness of 1025 photons/s/mm/mrad2/0.1% BW at 15 MeV and power of 6.7 PW are produced at laser intensity of 1.9 × 1023 W/cm2.
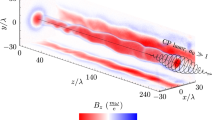
(a) 3D isosurface distributions for electron densities of the plasma channel (blue) and the helical electron bunch (red), where the isosurface values are respectively 30 nc and 50nc; part (b) shows the resonance curve of the transverse momentum with βrad/ωb = 0.01 (blue solid), 0.074 (red dash) and 0.15 (green solid); Inset of (b) shows the resonance bandwidth Δω with the radiation reaction factor βrad.
Theoretical Analysis
The properties of γ-ray radiation depend strongly on electron dynamics. Let’ s start with the dynamics of a single electron interacting with the laser and self-generated electromagnetic fields in laser-produced plasma channel by taking into account of the QED effects. In the ultrarelativistic limit  , the radiation reaction force can be approximately written as38,39,40
, the radiation reaction force can be approximately written as38,39,40

where FLL is the classical radiation reaction force in the Landau-Lifshitz form38. In order to take the quantum effect of radiation reaction force into account, we use a quantum-mechanically corrected factor Ge39,40, which reduces the amount of electrons’ unphysical energy loss due to the overestimation of the emitted photon energy in classical calculations. εrad = 4πre/3λ, re = e2/mec2 is the electron radius. β = v/c, aS = eES/meωc corresponds to the QED critical field ES ( ), and
), and  is the fine-structure constant. e, me, v are electron charge, mass, and velocity, respectively, ω0 and λ refer to laser frequency and wavelength, and c is light speed. The probability of γ-photon emission by an electron is characterized by the relativistic gauge-invariant parameter
is the fine-structure constant. e, me, v are electron charge, mass, and velocity, respectively, ω0 and λ refer to laser frequency and wavelength, and c is light speed. The probability of γ-photon emission by an electron is characterized by the relativistic gauge-invariant parameter  , where γe is the Lorentz factor. The QED effects are negligible for
, where γe is the Lorentz factor. The QED effects are negligible for  but play an important role for
but play an important role for  .
.
Assuming a CP plane laser propagating along x-direction, the laser fields are ELy = EL cos ϕ, ELz = EL sin ϕ, BLy = −ELz/νph, BLz = ELy/νph, where EL refers to their amplitude. The phase is ϕ = kx − ω0t and the phase velocity is νph = ω0/k, where ω0 and k are laser frequency and wave number. The self-generated electromagnetic fields in the plasma channel are assumed to be ESy, ESz, BSy, BSz transversely and BSx longitudinally. Considering the quantum radiation reaction force Eq. (1), the electron’s transverse motion in channel can be described as  , and
, and  , where κ = 1 − νx/νph and
, where κ = 1 − νx/νph and  . For high-energy electrons, it is reasonable to assume that
. For high-energy electrons, it is reasonable to assume that  ,
,  and
and  , as they are slowly-varying comparing with the fast-varying py and pz. Further assuming
, as they are slowly-varying comparing with the fast-varying py and pz. Further assuming  ,
,  , we obtain that
, we obtain that


Here  ,
,  and
and  . ωL = κω0 refers to laser frequency in the electron rest frame, and a0 = eEL/meω0c is the normalized laser amplitude. In Eqs (2) and (3), the third term Ωx is mainly distributed on the laser axis and can be neglected for the ultrarelativistic electrons in the electron bunch. Therefore, the betatron oscillation frequency can be estimated as
. ωL = κω0 refers to laser frequency in the electron rest frame, and a0 = eEL/meω0c is the normalized laser amplitude. In Eqs (2) and (3), the third term Ωx is mainly distributed on the laser axis and can be neglected for the ultrarelativistic electrons in the electron bunch. Therefore, the betatron oscillation frequency can be estimated as  . For electrons under resonance acceleration in laser fields, one can assume
. For electrons under resonance acceleration in laser fields, one can assume  , where Prad is the momentum amplitude and φ is its initial phase. Substituting py,z into Eqs (2) and (3), one has
, where Prad is the momentum amplitude and φ is its initial phase. Substituting py,z into Eqs (2) and (3), one has

From Eq. (4), the amplitude of electron transverse oscillation can be obtained as

On the one hand, Eqs (4) and (5) show that Prad and Rrad decrease when the radiation reaction factor βrad increases, that is, the transverse phase space of the electrons is confined by the radiation reaction force36. This helps trapping of a great amount of electrons in the plasma channel center. On the other hand, by taking dPrad/dωL = 0 from Eq. (4), one can get the resonance condition between laser frequency in the electron instantaneous rest frame and that of electron betatron oscillation ωr in the plasma channel as

Here, one can treat Eq. (4) as a function of Prad(ωL), and the resonance curves for different radiation reaction factors βrad are plotted in Fig. 1(b). It shows that the resonance bandwidth Δω, i.e., the full-width-at-half-maximum (FWHM) value of the resonance curve37, is significantly broadened when the radiation reaction factor βrad increases [See inset figure of Fig. 1(b)]. Results indicate that the resonance condition of the accelerated electrons is much relaxed. Both of these effects eventually result in formation of an ultradense electron bunch under resonant helical acceleration by laser, and hence emission of unprecedented brilliant vortical γ-ray pulses.
Simulation and Results
To verify our scheme, 3D PIC simulations are carried out using the QED-PIC code EPOCH41, which takes into account of the QED effects in the synchrotron radiation of γ-rays by using a Monte Carlo algorithm42. From Fig. 1(a), we clearly see that an ultradense helical electron bunch is formed in laser-produced plasma channel, which undergoes resonance acceleration by the laser pulses. For comparison, simulations with the QED calculation switched off are also carried out. Figure 2 plots electron density maps in plane z = 0 at different times for the cases with (upper row) and without (lower row) the QED effects taken into account. At early time t = 30T0 [2(a) and 2(e)], both of the cases show similar characters that a number of electrons are firstly injected into the center of the plasma channel. However, at later time t = 60T0, they show completely different physics. For the case without the QED effects, most electrons in the channel do not satisfy the narrow resonance condition, and the focusing force provided by the self-generated electromagnetic fields is not strong enough to offset the laser radial ponderomotive force31, so that they are expelled from the plasma channel, as shown in Fig. 2(f). For the case with the QED effects, as predicted by our theory, the radiation reaction force provides not only “trapping” but also“resonant” effects on electrons in the plasma channel, where a great amount of electrons are trapped and undergo direct resonance acceleration by intense lasers, shown in Fig. 2(b). At t = 80T0, in the case with QED effects, the transverse phase space of electrons is adequately confined by the radiation reaction recoil force, shown in Fig. 2(d), compared with that in Fig. 2(h). We see from Fig. 2(c) that an ultradense relativistic electron bunch with density above 100nc is formed in the channel under helical resonant motion in CP laser fields. Such an ultradense helical electron bunch leads to generation of strong axial magnetic field BSx up to 5.0 × 105T and azimuthal BSz up to 8.0 × 105T [See Fig. 3(a)]. The axial magnetic field helps to trap the background electrons near the laser axis undergoing pre-acceleration to hit the resonance condition32. The azimuthal magnetic field in turn not only provides additional confined forces to help trapping and achieving resonance acceleration of electrons, but also significantly enhances the probability of γ-photon emission29.
Density maps (in units of nc) of electrons in the plane z = 0 at t = 30T0 [(a) and (e)], 60T0 [(b) and (f)], 80T0 [(c) and (g)] for a CP laser pulse at intensity 1.9 × 1023 W/cm2 interaction with plasmas at densities 10nc in the cases with (upper row) and without (lower row) the QED effects taken into account, respectively. (d) and (h) show the corresponding transverse phase space distributions of electrons at 80T0.
Properties of resonant electrons in the channel of Fig. 2: (a) self-generated magnetic field BSz and BSx (normalised by meω0/e) in the plane z = 0 at t = 80T0; (b) and (c) typical electron motion trajectories ( ) and (
) and ( ), where the color bar shows increase of γe with time; (d) 3D isosurface distributions for electron energy density with the isosurface value at 1.2 × 104ncmec2; (e) the angular distribution of electrons; (f) the energy spectra of electrons in cases of with (red) and without (blue) the QED effects for CP laser and in the case of with QED effects for LP laser (green); Inset of (e) shows the distribution of the number of the electrons (energy above 500 MeV) with the polar angle.
), where the color bar shows increase of γe with time; (d) 3D isosurface distributions for electron energy density with the isosurface value at 1.2 × 104ncmec2; (e) the angular distribution of electrons; (f) the energy spectra of electrons in cases of with (red) and without (blue) the QED effects for CP laser and in the case of with QED effects for LP laser (green); Inset of (e) shows the distribution of the number of the electrons (energy above 500 MeV) with the polar angle.
Figure 3(b) shows the typical electron motion trajectories under resonance acceleration. It can be seen that the electrons are injected from the front interaction surface and the wall of the plasma channel. As the role of quantum radiation losses increases, the transverse phase space of these electrons is confined36, and they are easily trapped in the plasma channel. Further with the aid of the radiation reaction force, as expected, a great amount of these electrons undergo resonance acceleration in CP laser fields, whose energies increase dramatically (see the color evolutions of the lines). For electrons undergoing resonance acceleration, their energies are gradually transferred from the transverse component into the longitudinal one by the v × B force, whose  eventually decreases to a small value of 0.2, shown in Fig. 3(c). Figure 3(d) plots the energy density distribution of electrons at an isosurface value of 1.2 × 104ncmec2. It can be seen that an ultradense, helical relativistic electron bunch is formed, in which the electron maximum energy can reach 2 GeV [see 3(e) and 3(f)] and the total charge of electrons with energy above 500 MeV is about 200 nanoCoulomb [see the red line in 3(f)]. By comparing these high qualities of the beam with those without the QED effects, shown by the blue lines in Fig. 3(e) inset and 3(f), we conclude that the QED effects lead to great increase in the particle number and decrease in the divergence angle of high-energy electrons, in consistence with our theoretical expectations. The energy spectrum of electrons by using a LP laser with the same other parameters is shown by the green line in Fig. 3(f), which shows much lower cutoff energy and smaller number of high energy electrons, eventually leading to much weaker γ-ray emission.
eventually decreases to a small value of 0.2, shown in Fig. 3(c). Figure 3(d) plots the energy density distribution of electrons at an isosurface value of 1.2 × 104ncmec2. It can be seen that an ultradense, helical relativistic electron bunch is formed, in which the electron maximum energy can reach 2 GeV [see 3(e) and 3(f)] and the total charge of electrons with energy above 500 MeV is about 200 nanoCoulomb [see the red line in 3(f)]. By comparing these high qualities of the beam with those without the QED effects, shown by the blue lines in Fig. 3(e) inset and 3(f), we conclude that the QED effects lead to great increase in the particle number and decrease in the divergence angle of high-energy electrons, in consistence with our theoretical expectations. The energy spectrum of electrons by using a LP laser with the same other parameters is shown by the green line in Fig. 3(f), which shows much lower cutoff energy and smaller number of high energy electrons, eventually leading to much weaker γ-ray emission.
When the ultradense electron bunch undergoes resonance acceleration in CP laser fields, high-energy γ photons can be synchronously emitted. Figure 4(a) plots the 3D isosurface distribution of the γ-ray photon energy density at t = 80T0. It shows that a brilliant, vortical γ-ray pulse with energy density above 5.0 × 103 ncmec2, transverse size of 2 μm and duration of 40 fs is generated. The radiation power can increase to 18 J/T0 (6.7 PW) and then decrease with the dissipation of the laser pulse [See the inset figure of Fig. 4(c)], more γ photons and higher energy conversion efficiency from laser to γ-ray can be obtained when the laser pulse is fully dissipated. At t = 100T0, the total number of γ-ray photons with energy above 2.0 MeV is about 3.08 × 1014 with a 15.9 MeV mean energy, and the total energy of γ-ray photons is about 780 J, which corresponds to 22.91% from the laser energy, significantly higher than that in the case using LP laser (16.15%). The energy spectrum of the γ photons at 80T0 is plotted in Fig. 4(c). The maximum photon energy exceeds 1.0 GeV, and the peak brightness of the γ-ray pulse at 15 MeV is 1.4 × 1025 photons/s/mm2/mrad2/0.1% BW. At t = 100T0, it can arrive at 3.5 × 1025 photons/s/mm2/mrad2/0.1% BW. To the best of our knowledge, this is the γ-ray source with the highest peak brightness in tens-MeV regime ever reported in the literature. From Fig. 4(b), we can also see that the high-energy photons are highly collimated.
γ-ray pulse emitted in simulations: (a) 3D isosurface distribution of the γ-ray’s energy density at 5.0 × 103ncmec2; (b) the angular distribution of γ-ray energy for photons with energy above 2.0 MeV, where the polar and azimuthal angles are θ and φ, respectively; (c) the energy spectrum of photons, where the photon number is calculated in 0.1% bandwidth (BW); The inset in (c) shows the total radiation power Pph = Wph/T0, which is defined as the emitted photon energy per laser period.
Discussion
The scaling properties of the emitted γ-rays by the proposed scheme have also been investigated. For a fixed self-similar parameter S = ne/a0nc = 1/30, which strongly determines the electron dynamics in near-critical plasmas as discussed in ref. 43, a series of simulations are carried out with different laser intensities, i.e., a0. As shown in Fig. 5(c), our scheme still works at lower a0 = 150, though the density of the electron bunch drops, which leads to lower energy conversion efficiency of 8.0% from laser pulse to γ photons [Fig. 5(a)]. When the laser intensity increases, the energy conversion efficiency from laser to electrons drops and that from laser to photons grows up to 27% and then becomes saturate, shown by the blue lines in Fig. 5(a). And due to the enhanced resonance acceleration under stronger radiation reaction recoil force and self-generated electromagnetic fields, both the number and mean energy of the emitted γ-photons increase as well with the laser intensity, shown in Fig. 5(b). Different from the previous theoretical and numerical results 43, which is based on the betatron radiation properties in the non-QED regime with linearly polarized lasers (a0 ≤ 80), here the scaling shows to be as linear as Nph ∝ a0 and  respectively.
respectively.
The scaling properties of the emitted γ-ray: (a) the conversion efficiencies from laser to electrons (black) and photons (blue) varying with different laser amplitude a0; (b) the photon number (black) and mean energy (red) varying with a0. (c) and (d) Respectively show the density maps (in units of nc) of electrons in the plane z = 0 for the case at normalized laser intensity of a0 = 150 and the case with a reasonable temporal profile of a = 250 sin2(πt/22T0).
To verify that our scheme still works for a more reasonable laser pulse, an additional simulation is performed. The laser pulse has a exact temporal profile of a = 250sin2(πt/22T0) with a duration of 11T0 (29.3 fs) and total energy of 266 J, which can be achieved, for example, with the ELI laser24 under development and Vulcan44 (planned updating) in the near future. The electron density map in plane z = 0 is plotted in Fig. 5(d). It can be clearly seen that an ultradense electron bunch is still formed undergoing stable resonance acceleration in the plasma channel and then brilliant γ-ray pulse is generated. As a result, 4.1 × 1013 γ photons are emitted and the energy conversion efficiency from laser pulse to γ photons can reach as high as 33%. Therefore, this robust electron acceleration and γ-ray emission scheme still works if a more reasonable laser pulse is used.
In this paper, we have reported a novel electron resonance acceleration scheme in the QED regime of CP laser-plasma interactions, where the quantum radiation loss helps trapping of electrons and the radiation reaction recoil force significantly relaxes the resonance condition between electrons and lasers. A great amount of electrons gather around the center of the plasma channel and undergo resonance acceleration, forming an ultradense, vortical relativistic electron bunch. As a result, unprecedentedly brilliant petawatt γ-ray pulses can be obtained.
Methods
The 3D PIC simulations are carried out using the QED-PIC code EPOCH. In the simulations, 900 cells longitudinally along the x axis and 2402 cells transversely along y and z axes constitute a 75 × 20 × 20λ3 simulation box. A fully-ionized hydrogen plasma target with an uniform electron density of 1.7 × 1022 cm−3 (10nc) is located from x = 5 to 75 λ. Each cell of plasma is filled with 12 pseudoelectrons and 12 pseudoprotons. A CP laser pulse with peak intensity 1.9×1023 W/cm2 and wavelength λ = 0.8 μm propagates from the left boundary into target. The laser pulse has a transverse Gaussian profile of FWHM radius r0 = 4λ and a square temporal profile of durations τ = 60T0 (T0 = 2π/ω0), which is composed of 30 T0 sinusoidal rising and 30 T0 constant parts.
The resonance curve of the transverse momentum in Fig. 1(b) is obtained by Eq. (4). The value βrad/ωb = 0.074 is estimated from the parameters gotten in our simulation. For comparison in Fig. 3(f), under the premise of ensuring the same laser intensity, we have also carried out simulations that the incident laser is linearly polarized. The spectrums here are for electrons within a radius of 3 λ and a spreading angle of 0.38 rad. To investigate the scaling properties of the emitted γ-ray in Fig. 5, we fix the self-similar parameter S = 1/30 and the other parameters in the simulations are same. In order to check the accuracy of our simulation results, we have also carried out the simulation at a higher resolution with spatially half of the current grid size, which shows almost the same results as here.
Additional Information
How to cite this article: Chang, H. X. et al. Brilliant petawatt gamma-ray pulse generation in quantum electrodynamic laser-plasma interaction. Sci. Rep. 7, 45031; doi: 10.1038/srep45031 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Nerush, E. N. et al. Laser field absorption in self-generated electron-positron pair plasma. Phys. Rev. Lett. 106, 035001 (2011).
Ridgers, C. P. et al. Dense electron-positron plasmas and ultraintense γ-rays from laser-irradiated solids. Phys. Rev. Lett. 108, 165006 (2012).
Chang, H. X. et al. Generation of overdense and high-energy electron-positron-pair plasmas by irradiation of a thin foil with two ultraintense lasers. Phys. Rev. E 92, 053107 (2015).
Hegelich, B. M. et al. Laser acceleration of quasi-monoenergetic MeV ion beams. Nature 439, 441–444 (2006).
Ganz, J. Gamma Knife Neurosurgery (Springer-Verlag, Wien, 2011).
Wardle, J. F. C., Homan, D. C., Ojha, R. & Roberts, D. H. Electron-positron jets associated with the quasar 3C279. Nature 395, 457–461 (1998).
Aharonian, F. A. et al. High-energy particle acceleration in the shell of a supernova remnant. Nature 432, 75–77 (2004).
Ballam, J. et al. Total and partial photoproduction cross sections at 1.44, 2.8, and 4.7 GeV. Phys. Rev. Lett. 23, 498–501 (1969).
Schoenlein, R. W. et al. Femtosecond x-ray pulses at 0.4 Å generated by 90° Thomson Scattering: A tool for probing the structural dynamics of materials. Science 274, 236–238 (1996).
Corde, S. et al. Femtosecond x rays from laser-plasma accelerators. Rev. Mod. Phys. 85, 1–48 (2013).
Giulietti, A. et al. Intense γ-ray source in the giant-dipole-resonance range driven by 10-TW laser pulses. Phys. Rev. Lett. 101, 105002 (2008).
Courtois, C. et al. Effect of plasma density scale length on the properties of bremsstrahlung x-ray sources created by picosecond laser pulses. Physics of Plasmas 16, 013105 (2009).
Galy, J., Maučec, M., Hamilton, D. J., Edwards, R. & Magill, J. Bremsstrahlung production with high-intensity laser matter interactions and applications. New Journal of Physics 9, 23 (2007).
Ledingham, K. W. D. & Galster, W. Laser-driven particle and photon beams and some applications. New Journal of Physics 12, 045005 (2010).
Chen, H. et al. Relativistic positron creation using ultraintense short pulse lasers. Phys. Rev. Lett. 102, 105001 (2009).
Chen, H. et al. Relativistic quasimonoenergetic positron jets from intense laser-solid interactions. Phys. Rev. Lett. 105, 015003 (2010).
Sarri, G. et al. Ultrahigh brilliance multi-MeV γ-ray beams from nonlinear relativistic Thomson Scattering. Phys. Rev. Lett. 113, 224801 (2014).
PhuocK., T. et al. All-optical compton gamma-ray source. Nat Photon 6, 308–311 (2012).
Thomas, A. G. R., Ridgers, C. P., Bulanov, S. S., Griffin, B. J. & Mangles, S. P. D. Strong radiation-damping effects in a gamma-ray source generated by the interaction of a high-intensity laser with a wakefield-accelerated electron beam. Phys. Rev. X 2, 041004 (2012).
Powers, N. D. et al. Quasi-monoenergetic and tunable x-rays from a laser-driven compton light source. Nat Photon 8, 28–31 (2014).
Liu, C. et al. Generation of 9 MeV γ-rays by all-laser-driven compton scattering with second-harmonic laser light. Opt. Lett. 39, 4132–4135 (2014).
Sarri, G. et al. Generation of neutral and high-density electron-positron pair plasmas in the laboratory. Nat Commun 6, 6747 (2015).
Martinez, M. et al. In Boulder Damage Symposium XXXVII: Annual Symposium on Optical Materials for High Power Lasers, (SPIE-International Society for Optical Engineer- ing, Bellingham, WA), p. 59911N (2005).
The extreme light infrastructure: http://www.eli-laser.eu.
Nakamura, T. et al. High-power γ-ray flash generation in ultraintense laser-plasma interactions. Phys. Rev. Lett. 108, 195001 (2012).
Brady, C. S., Ridgers, C. P., Arber, T. D., Bell, A. R. & Kirk, J. G. Laser absorption in relativistically underdense plasmas by synchrotron radiation. Phys. Rev. Lett. 109, 245006 (2012).
Brady, C. S., Ridgers, C. P., Arber, T. D. & Bell, A. R. Synchrotron radiation, pair production, and longitudinal electron motion during 10–100 PW laser solid interactions. Physics of Plasmas 21, 033108 (2014).
Brady, C. S., Ridgers, C. P., Arber, T. D. & Bell, A. R. Gamma-ray emission in near critical density plasmas. Plasma Physics and Controlled Fusion 55, 124016 (2013).
Stark, D. J., Toncian, T. & Arefiev, A. V. Enhanced multi-MeV photon emission by a laser-driven electron beam in a self-generated magnetic field. Phys. Rev. Lett. 116, 185003 (2016).
Breit, G. & Wheeler, J. A. Collision of two light quanta. Phys. Rev. 46, 1087–1091 (1934).
Ji, L. L., Pukhov, A., Kostyukov, I. Y., Shen, B. F. & Akli, K. Radiation-reaction trapping of electrons in extreme laser fields. Phys. Rev. Lett. 112, 145003 (2014).
Liu, B. et al. Generating overcritical dense relativistic electron beams via self-matching resonance acceleration. Phys. Rev. Lett. 110, 045002 (2013).
Hu, R. et al. Dense helical electron bunch generation in near-critical density plasmas with ultrarelativistic laser intensities. Scientific Reports 5, 15499 (2015).
Pukhov, A., Sheng, Z. M. & Meyer-ter-Vehn, J. Particle acceleration in relativistic laser channels. Physics of Plasmas 6, 2847–2854 (1999).
Gahn, C. et al. Multi-MeV electron beam generation by direct laser acceleration in high-density plasma channels. Phys. Rev. Lett. 83, 4772 (1999).
Green, D. G. & Harvey, C. N. Transverse spreading of electrons in high-intensity laser fields. Phys. Rev. Lett. 112, 164801 (2014).
Landau, L. D. & Lifshitz, E. M., Mechanics: Volume 1 of Course of Theoretical Physics (Elsevier, Oxford, 1976).
Landau, L. D. & Lifshitz, E. M., The Classical Theory of Fields, (Pergamon, Oxford, 1975).
Bulanov, S. S., Schroeder, C. B., Esarey, E. & Leemans, W. P. Electromagnetic cascade in high-energy electron, positron, and photon interactions with intense laser pulses. Phys. Rev. A 87, 062110 (2013).
Esirkepov, T. Z. et al. Attractors and chaos of electron dynamics in electromagnetic standing waves. Physics Letters A 379, 2044–2054 (2015).
Arber, T. D. et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Physics and Controlled Fusion 57, 113001 (2015).
Duclous, R., Kirk, J. G. & Bell, A. R. Monte carlo calculations of pair production in high-intensity laser-plasma interactions. Plasma Physics and Controlled Fusion 53, 015009 (2011).
Huang, T. W. et al. Characteristics of betatron radiation from direct-laser-accelerated electrons. Phys. Rev. E 93, 063203 (2016).
The vulcan 10 petawatt project: http://www.clf.stfc.ac.uk/CLF/Facilities/Vulcan/The+Vulcan+10+Petawatt+Project/14684.aspx
Acknowledgements
This work is supported by the National Natural Science Foundation of China, Grants No. 11575298, No. 91230205, No. 11575031, and No. 11175026; the NSAF, Grant No. U1630246; the National key research and development program No. 2016YFA0401100; the National Science Challenging Program; the National Basic Research 973 Projects No. 2013CBA01500 and No. 2013CB834100, and the National High-Tech 863 Project. B.Q. acknowledges the support from the Thousand Young Talents Program of China. M.Z. acknowledge support from the Engineering and Physical Sciences Research Council (EPSRC), Grant No. EP/1029206/1. The computational resources are supported by the Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase). H.X.C. acknowledges the comments and suggestions from the anonymous referees.
Author information
Authors and Affiliations
Contributions
B.Q., C.T.Z. and X.T.H. conducted the work. B.Q., H.X.C.,T.W.H. and Z.X. developed the basic theory. H.X.C. carried out all simulations. Some detail of the physics are clarified by Y.Q.G., X.Q.Y. and M.Z. The manuscript is written by H.X.C. and B.Q. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chang, H., Qiao, B., Huang, T. et al. Brilliant petawatt gamma-ray pulse generation in quantum electrodynamic laser-plasma interaction. Sci Rep 7, 45031 (2017). https://doi.org/10.1038/srep45031
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep45031
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.