Abstract
Transition metal dichalcogenides (TMDs) WTe2 and MoTe2 with orthorhombic Td phase, being potential candidates as type-II Weyl semimetals, are attracted much attention recently. Here we synthesized a series of miscible Mo1−xWxTe2 single crystals by bromine vapor transport method. Composition-dependent X-ray diffraction and Raman spectroscopy, as well as composition and temperature-dependent resistivity prove that the tunable crystal structure (from hexagonal (2H), monoclinic (β) to orthorhombic (Td) phase) can be realized by increasing W content in Mo1−xWxTe2. Simultaneously the electrical property gradually evolves from semiconductor to semimetal behavior. Temperature-dependent Raman spectroscopy proves that temperature also can induce the structural phase transition from β to Td phase in Mo1−xWxTe2 crystals. Based on aforementioned characterizations, we map out the temperature and composition dependent phase diagram of Mo1−xWxTe2 system. In addition, a series of electrical parameters, such as carrier type, carrier concentration and mobility, have also been presented. This work offers a scheme to accurately control structural phase in Mo1−xWxTe2 system, which can be used to explore type-II Weyl semimetal, as well as temperature/composition controlled topological phase transition therein.
Similar content being viewed by others
Introduction
Recently, layered transition metal dichalcogenides (TMDs) materials have attracted extensive attention because of their superior properties, for example, large thermoelectric effect in TiSe2 at room temperature1, superconductivity2, charge density waves3, extremely large magnetoresistance in WTe24, topological phase5,6 and next-generation (opto-) electronics devices7,8. Among these transition metal dichalcogenides, hereafter we focus on Mo1−xWx (Te, Se, S)2 compounds.
Mo1−xWx(S, Se, Te)2 compounds demonstrate a rich crystal structures and diversified physical properties9,10,11,12. In the viewpoint of crystal structure, Mo1−xWx (Te, Se, S)2 can crystallize into three phases under different experimental conditions, including 2H- (hexagonal, space group P63/mmc), Td- (orthorhombic, space group Pmn21) and β-phase (monoclinic, space group P21/m), as shown in Fig. 1(a)13. The common structure of MoTe2 is 2H-phase, while the WTe2 is normally taken Td-phase. The β-phase MoTe2, a metastable phase, can also be obtained by quenching method at high temperature of about 1173 K14,15. It has the inversion symmetry which does not in Td phase. In addition, these phases may be changed under thermal agitation, for example, MoTe2 has a first-order structural phase transition (around 250 K) from the β to the Td polytype15,16. In the viewpoint of physical properties, generally speaking, the 2H phase is a semiconductor, but Td and β phase are semi-metallic. For example, 2H-phase Mo1−xWxS2 and Mo1−xWxSe2 are semiconductors whose electronic band gap can be continuously tuned by alloy9,10,11,12. While, MoTe2 compounds with β and Td phase show the metallic conductivity. It should be emphasized that both MoTe2 and WTe2 with Td phase belong to a type-II topological Weyl semimetal according to recent theoretical predictions17,18. The condensed matter physics counterparts of Weyl fermions have been realized firstly in type-I Weyl semimetals in the TaAs family19,20,21,22. Different from type-I Weyl semimetal, Dirac cone in type-II Weyl semimetal is tilted17,18. Currently, several angle-resolved photoemission spectroscopy and transport works have claimed to observe the Fermi arc and tilted Dirac cones in type-II Weyl semimetals of WTe2 and MoTe223,24,25,26,27,28. In addition, Mo1−xWxTe2 can demonstrate the topological phase transition under thermal agitation or alloy. For example, the length of Fermi arc in Td phase WTe2 is tunable by temperatures or by Mo-alloy as theoretically predicted29,30.
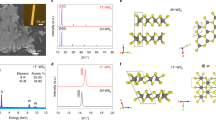
(a) Crystal structure of Mo/WTe2 (2H, β and Td phase, respectively). (b) Schematic of the double-zone CVT growth furnace and the growth process of Mo1−xWxTe2 single crystals. (c) SEM image and W (red), Mo (green) and Te (blue) element mapping images of Mo0.5W0.5Te2 single crystal. (d) The XRD patterns of representative Mo1−xWxTe2 single crystals. (e) The enlarged (002) XRD peaks for all samples.
Here we summarized the previous effort to elucidate the phase transition in Mo1−xWxTe2. For β-MoTe2, there is a phase transition from the β to the Td polytype at about 250 K in β-MoTe215,16. It is worthwhile to mention that the Td-phase is an important candidate to materialize the newly predicted type-II Weyl semimetal. Type-II Weyl semimetals have a series of novel physical properties, such as anisotropic negative magentoresistance, topological anomalous Hall effect17,18. The transition from β- to Td-phase is also characterized by the temperature-dependent XRD31,32, as well as temperature-dependent Raman spectroscopy33,34. However, the existence of orthorhombic Td phase MoTe2 is still under hot debate because it is quite challenging to directly distinguish the subtle differences between the Td and β phase. As for the Mo1−xWxTe2 system, there are some experimental studies on ceramic samples35,36 and theoretical predictions on monolayers37,38, but no any phase-transitions works for single crystal samples at present, to the best of our knowledge.
Based on above-mentioned discussions, it is quite crucial to map out the phase diagram of Mo1−xWxTe2 at different temperature and their corresponding electrical properties in order to explore the type-II topological Weyl semimetals and corresponding novel physical properties in this system. Here, we synthesized a series of Mo1−xWxTe2 single crystals by the chemical vapour transport method. X-ray diffraction and chemical composition analysis confirm that the obtained samples have single crystalline quality, in which the Mo and W elements are miscible. The composition-dependent and temperature-dependent phase evolutions in Mo1−xWxTe2 are determined by Raman spectroscopic characterization. These characterizations substantiate that by increasing the W composition, the crystal structure of Mo1−xWxTe2 gradually changes from 2H, β to Td phase13. Simultaneously, the electrical properties gradually evolve from semiconductor to semimetal behavior revealed by temperature-dependent resistivity and Hall curves. Based on these data, we also map out the composition- and temperature-dependent phase diagram of Mo1−xWxTe2 system.
Methods
Crystal Growth
A series of Mo1−xWxTe2 single crystals were prepared by the chemical vapor transport (CVT) method that is discussed in detail elsewhere39. Figure 1(b) shows a schematic of the double-zone CVT growth furnace with well-controlled temperature. The single-crystal growth procedure includes two steps. Firstly, all Mo1−xWxTe2 polycrystalline samples were synthesized by heating a stoichiometric mixture of high purity elemental powders W (Alfa Aesar 99.99%), Mo (Alfa Aesar 99.99%) and Te (Alfa Aesar 99.999%) by solid state reaction at 1073 K in evacuated quartz tubes. Secondly, Mo1−xWxTe2 crystals were grown by CVT method using Br2 (about 5 mg/mL) as transport agent in the sealed evacuated quartz tube at a double zone furnace. By means of optimized the growth parameters, large size (centimetre-level) and high-quality crystals with regular shape can be obtained. The β-MoTe2 crystals can be grown at high temperature profile of 1173~1273 K. The growth quartz tube was quenched in ice water to yield the high-temperature β phase. And 2H-MoTe2 and Td-WTe2 crystals were obtained with a temperature profile of 1023~1123 K using usual cooling treatment (100 K/h) without quenching.
Material Characterization
The elemental compositions of the samples were determined by energy dispersive X-ray spectroscopy (EDS) analysis conducted on an FEI Quanta 200 FEG environmental scanning electron microscope (SEM). X-ray diffraction (XRD) measurements were performed on the crystals using an X-ray diffractometer (Ultima III Rigaku, Cu-Kα radiation as an X-ray source). The scanning rate of 3° per minute and 2θ scanned from 10° to 70° were used to collect XRD data. Raman spectra were taken by a backscattering geometry on a LabRam HR800 Microscope system (Horiba Jobin Yvon), using the 633 nm a He-Ne laser as an optical source. Standard four-probe technique was used for resistivity and Hall-effect measurements on a Quantum Design PPMS-9.
The density functional theory (DFT) Calculation
The Raman frequencies of MoTe2 and WTe2 for different structures were calculated by DFT in the generalized gradient approximation implemented in the Vienna Ab-initio Simulation Package (VASP) code40,41 and the Phonopy software42. The projected augmented wave method43,44 and the van der Waals corrected optB86b-vdw functional45,46 are used. The plane-wave cutoff energy is 500 eV throughout the calculations. The k point mesh is 12 × 12 × 4 for the 2H phase and 8 × 14 × 4 for the β- and Td-phase. The atom positions and lattice constants are optimized until the maximal residual force is less than 0.002 eV/Å. The optimized lattice constants are very well consistent with the reported values which are shown in Table S1 at Supplementary Information.
Results and Discussion
Figure 1(c) depicts the SEM images of the as-grown Mo0.5W0.5Te2 crystals and the corresponding EDS mapping of Mo, W and Te elements, respectively. As can be seen, the three elements are uniformly distributed in the sample, strongly suggesting the growth is homogeneous. The composition analysis substantiates that the composition ratio between Mo and W in this sample is 1.00:1.02, which is in agreement to the designed chemical compositions. All the EDS spectra of the as-grown Mo1−xWxTe2 crystals are depicted in Fig. S1. The elemental compositions of all the crystal samples and cross section used in EDS analysis are shown in Table II and III in Supplementary Information. The XRD patterns of single crystal samples are presented in Fig. 1(d). All peaks indexed as the (0 0 2k) reflections, indicating that the exposed surfaces of the crystals belong to c-plane. The full-width at half maximum of Mo1−xWxTe2 (002 pole) series samples varies from 0.07° to 0.09°, which infers the as-grown single crystals have high crystalline quality. In order to show the effect of isovalent substitution on the crystal structure clearly, we enlarge of the series (002) peaks in Fig. 1(e) for all Mo1−xWxTe2 samples. It is evident that there are three continuous change regimes (x = 0~0.07, 0.10~0.50, and 0.70~1, respectively), which implies there may be three different phases. This may be due to the different lattice parameter c of 2H-MoTe2, β-MoTe2 and Td-WTe2 (13.97, 13.86, and 14.07 Å, respectively) that causes the angle-shift of the (002)-peaks13. In addition, we also can see that the diffraction peaks gradually shift to lower angle degree with increasing x within each concentration range. This is because that the lattice parameter c changes large due to the ionic radius of W4+ (0.66 Å) being larger than that of Mo4+ ions (0.65 Å)39,47. But, by careful inspection, we find that from x = 0.08 to 0.10 and from x = 0.50 to 0.70, the diffraction (002) peaks gradually shift to higher angle degree with increasing x (W composition). The estimated c-axis lattice parameter dc as a function of x for Mo1−xWxTe2 system and β-MoTe2 is given as Fig. S2 at Supplementary Information. So it may be reasonable to conclude that the phase transitions occur from x = 0.08 to 0.1 and from x = 0.50 to 0.70. Crystal structures of Mo1−xWxTe2 compounds change from 2H, β to Td phase with increasing x.
In order to substantiate the composition-dependent structure phase transitions, Raman spectra measurements were further used to characterize these single crystals at room temperature. Figure 2 shows the normalized un-polarized Raman spectra from the ab plane of the as-grown Mo1−xWxTe2 single crystalline samples and the Raman spectrum of pure β-MoTe2 obtained from high temperature quenching (upmost in Fig. 2). Obviously, there are three different types of Raman spectra mapped to different x range (0~0.09, 0.10~0.50, and 0.70~1, respectively) and the Raman spectrum of β-MoTe2 (upmost) is in good agreement with that of x from 0.1 to 0.50. These general trends are in agreement to XRD results.
To understand the Raman modes of different crystalline phases in the Mo1−xWxTe2 system, we also calculated the Raman frequencies by the DFT and the results are well consistent with the experimental one (see Fig. S3 at Supplementary Information). According to the group theory analysis, the irreducible representations of the phonons in bulk 2H-MoTe2 ( point group) at the center (Γ point) of the Brillouin zone (BZ) are
point group) at the center (Γ point) of the Brillouin zone (BZ) are  , where E2g (24.993 and 230.043 cm−1), E1g (116.540 cm−1), A1g (171.893 cm−1) are Raman-active. In bulk β-MoTe2 or WTe2 (
, where E2g (24.993 and 230.043 cm−1), E1g (116.540 cm−1), A1g (171.893 cm−1) are Raman-active. In bulk β-MoTe2 or WTe2 ( ), the calculated phonon modes at the Γ point include
), the calculated phonon modes at the Γ point include  , where there are 18 Raman active phonon modes (12Ag + 6Bg), as shown in Fig. S3. Bulk Td-MoTe2 and Td-WTe2 both belong to the
, where there are 18 Raman active phonon modes (12Ag + 6Bg), as shown in Fig. S3. Bulk Td-MoTe2 and Td-WTe2 both belong to the  point group, the group theory analysis indicates that the BZ-center vibration modes decompose into 36 one-dimensional irreducible representations:
point group, the group theory analysis indicates that the BZ-center vibration modes decompose into 36 one-dimensional irreducible representations:  , where all modes are Raman active (see Fig. S3). All the above calculation results are in agreement with the previous theoretical works48,49,50.
, where all modes are Raman active (see Fig. S3). All the above calculation results are in agreement with the previous theoretical works48,49,50.
To analyse the Raman results of Mo1−xWxTe2 compounds, the Raman results of some pure phases are mentioned here firstly. As depicted in Fig. 2, in Raman spectra measurements of 2H-MoTe2 (the bottom black line), we detect two sharp peaks at 172.8 and 232.9 cm−1 which are attributed to the A1g and E2g modes, respectively. For β-MoTe2 crystals (see upmost line of Fig. 2), we observe six Raman peaks at around 78.0, 88.0, 94.0, 127.4, 162.2 and 256.8 cm−1, associated with the Ag and Bg modes, respectively. And in the Raman spectrum of Td-WTe2 (the second line from the top in Fig. 2), there are eight peaks centred at 80.2, 90.0, 111.3, 116.2, 131.7, 133.5, 162.8 and 210.3 cm−1, respectively, which are ascribed to the A1 and A2 modes. These experimental Raman frequencies are very well reproduced by our DFT calculations (see Fig. S3 in Supplementary Information).
Using the above-mentioned Raman data in the pure phases, we can track the composition-dependent structure evolution in the whole Mo1−xWxTe2 systems. The evolutions of the prominent Raman peaks for different x in three frequency-ranges are plotted in Fig. 3(a–c). And the corresponding shifts of these peaks as functions of x are summarized in Fig. 3(d), respectively. We compare the Raman active modes of the three phases, two prominent peaks, A1g (near 171.893 cm−1) and E2g (near 230.043 cm−1), in the 2H phase spectra are assigned as fingerprint peaks. Because there are no Raman active modes near the above two positions in β and Td phases. As shown in Fig. 3(a), from x = 0 to 0.09, two prominent peaks were observed at about 173 and 233 cm−1, respectively. These two peaks are related to the A1g and E2g modes of 2H-MoX2, confirming the corresponding samples being 2H phase. Figure 3(d) indicates that there is no noticeable frequency change of the two peaks with the x composition increased from 0 to 0.09. But the intensity and full-width-at half-maximum of A1g and E2g mode in 2H phase are irregularly dependent on W-concentration, whose mechanism will be explored in the near future. It also should be mentioned that according to a previous report51, the Raman spectrum was strongly dependent on electron/hole doping in single layered MoS2. In that case, Fermi level adjustment should affect electron/hole concentration, which will in turns affect the electron-phonon scattering and Raman peaks. Different from this scenario, iso-valence W-doping to Mo in our samples does not induce significantly the electron/hole concentration, therefore the peaks of A1g and E2g have not obviously changed as shown in Fig. 3(d).
(a) Raman spectra (150~300 cm−1) of Mo1−xWxTe2 single crystals with composition x in the range of 0~0.09. (b) Raman spectra (I: 120~150 cm−1; II: 150~300 cm−1) of β-MoTe2 and Mo1−xWxTe2 single crystals with x composition in the range of 0.1~0.5. (c) Raman spectra (I: 120~150 cm−1; II: 150~300 cm−1) of Mo1−xWxTe2 single crystals with x composition in the range of 0.7~1.0. (d) Composition-dependent Raman frequencies of β-MoTe2 and Mo1−xWxTe2 single crystals (x = 0~1.0). All the Raman spectra were measured at room temperature.
According to the previous works33,34, the evolution of the Raman mode at near 130 cm−1 is a direct verification of the structural phase transition of MoTe2 from high temperature β to low temperature Td phase. In addition, there are different Raman signals for β- and Td-phase at the range of 150~300 cm−1. Here we used peaks from 120 to 300 cm−1 to determine the β-Td phase transition. The Raman peaks around 130 cm−1, and those from 150 to 300 cm−1 are enlarged in Fig. 3(b) and (c) for β-MoTe2 and the Mo1−xWxTe2 (x = 0.1~1.0), respectively. We can see that from x = 0.1 to 0.5 there is only one peak found near 127 cm−1 in the Raman spectra between 120~150 cm−1, as well as β-MoTe2 (see Fig. 3(b-I)). The position of this peak exhibits slight red-shift compared with that of β-MoTe2 (see Fig. 3(d)). There are also two peaks found at around 162 and 257 cm−1 in the Raman spectra of Mo1−xWxTe2 crystals (x = 0.1~0.5) (see Fig. 3(b-II)), which agree to the Raman signal (Ag modes) of β-MoTe2. From Fig. 3(d), it can be seen that the positions of the peaks (162 and 257 cm−1) exhibit slight blue-shift compared with that of β-MoTe2. The above results infer that these samples within x = 0.1~0.5 may belong to β-phase. On the other hand, when x changed into the range of 0.7–1.0, we find a multiple peak at around 130 cm−1 in the Raman spectra between 120~150 cm−1 (shown in Fig. 3(c-I)). The whole peak is fitted by the Lorentz function. As shown in Fig. 3(c-I), the experimental peaks can be fitted with two Lorentz line shapes with central peaks at approximately 130 and 133 cm−1, respectively. It suggests that the compound structure change from β to Td phase and the Mo1−xWxTe2 samples with x ranged from 0.7 to 1.0 have Td structure. Compared with pure Td-WTe2, the positions of the two peaks (near 130 and 133 cm−1) in all other samples exhibit red-shift and the difference is increased gradually with Mo composition increased (see Fig. 3(d)). In addition, from x = 0.7 to 1, we detect another two peaks at around 162 and 210 cm−1 in the Raman spectra measurements (shown in Fig. 3(c)-II), confirming all the Mo1−xWxTe2 samples (x = 0.7~1) belong to Td phase too. The positions of the two peaks in all other samples exhibit red-shift compared to pure Td-WTe2 (see Fig. 3(d)).
It is worth mentioning the Raman spectra of Mo0.7W0.3Te2, Mo0.5W0.5Te2 and M0.3W0.7Te2 are enlarged in Fig. S4. In Mo0.5W0.5Te2, except the characteristic peaks of β phase, there is a very weak peak around 210 cm−1, which is likely to be related to the Raman signal of the A1 modes of Td phase33. And broad Raman peak at around 130 cm−1 of Mo0.5W0.5Te2 also could be approximately as overlap of multiple peaks. These results indicate that Mo0.5W0.5Te2 have mixture of β- and Td-phase. In addition, a low-intensity peak around 264 cm−1 is observed in the Mo0.3W0.7Te2 Raman spectrum, which is contributed to the Raman signal of the Ag modes in β-MoTe2. It suggests that around x = 0.7, the phase can be approximately changed into β phase. Based on above-mentioned analysis, we conclude that the samples with x range of 0~0.09, 0.10~0.50, and 0.70~1, belong to 2H-, β- and Td phase, respectively. And at the range of x = 0.5~0.7, the phase of Mo1−xWxTe2 can be ascribed to be a mixing phase of β and Td. The critical compositions of phase transition in the Mo1−xWxTe2 system are approximately located at around x = 0.1 and 0.5, respectively.
Except the composition-dependent structure phase transition, we further characterized the temperature-dependent structure phase transition in Mo1−xWxTe2 compounds. As shown in Fig. 4(a) and (b), with decreasing the temperature of 2H-MoTe2 and Td-WTe2 samples from 300 to 100 K, no new Raman peaks appear although all peaks exhibit different blue-shift. This result implies that no temperature phase transition occurs in 2H-MoTe2 and Td-WTe2 systems at low-temperature range under atmospheric pressure. In Fig. 4(c), we present temperature-dependent Raman spectra for β-MoTe2 at the range between 100~300 K. One can see the intensity of all peaks is strengthened although the magnitude of the blue-shift is different. Surprisingly, at around 240 K, the Raman peaks of 129 cm−1 become two new peaks at about 127 and 132 cm−1, respectively, reaching the maximum intensity below 200 K, as highlighted in pink wireframe. In accordance with previous analysis33,34 and our calculation results, the two new Raman peaks occur only at the low temperature Td phase in the Mo1−xWxTe2 system. It suggests that splitting of this Raman peak may infer the structural phase transition in β-MoTe2. In order to verify the low-temperature phase transition, we also characterized the temperature dependence Raman spectra on Mo0.9W0.1Te2 of β phase. The evolution of the peak 129 cm−1 is shown in Fig. 4(d). Upon cooling, the peak develops into two new Raman peaks at about 280 K, confirming that the two sample change from high temperature β to low temperature Td phase.
Based on the above analysis, we plot a structural phase diagram of Mo1−xWxTe2 as functions of composition x and the temperature in Fig. 5. It is evident that 2 H phase appears in a composition range from x = 0 to 0.09 at room temperature and pure 2H-MoTe2 transforms into the high-temperature phase β-MoTe2 at about 1173 K14,15. β phase exists in a composition range of x = 0.1~0.5 at room temperature and would change from β to low temperature Td phase at 240~300 K. Td phase is a candidate of type-II Weyl semimetal, so the corresponding phase transition can be designated as the temperature-induced topological phase transition. In the Mo1−xWxTe2 alloys, Td phase (a candidate of type-II Weyl semimetal) lies in a composition x range of 0.7~1, but they have no temperature-dependent phase transitions. In addition, at the range of x = 0.5~0.7, the phase of Mo1−xWxTe2 can be described as a mixing phase of β and Td.
The electrical properties of the Mo1−xWxTe2 compounds were also characterized. As shown in Fig. 6(a), from x = 0 to 0.09, the Mo1−xWxTe2 samples all show the semiconductor behavior. While the other Mo1−xWxTe2 samples with a composition range of x = 0.1~1 and β-MoTe2 samples show the semi-metallic behavior as presented in Fig. 6(b). Interestingly, for β-MoTe2 and Mo0.9W0.1Te2, obvious electrical resistivity anomalies are observed at 250 and 230 K respectively, which are associated with the structural phase transition from the β to Td phase. However, there are no resistivity anomaly appeared in the temperature-dependent-resistivity curves of Mo1−xWxTe2 samples (x = 0.15~0.50). In addition, the resistivity of Td-WTe2 below 71 K (see upper inset of Fig. 6(c)) can be well fitted by
(a) Temperature-dependent ab-plane resistivities ρxx of Mo1−xWxTe2 single crystals (x = 0~0.09). (b) Temperature-dependent ab-plane resistivities ρxx of β-MoTe2 and Mo1−xWxTe2 single crystals (x = 0.1~1). (c) Composition-dependent of T* in Mo1−xWxTe2 single crystals (x = 0.1~1). Red globule represents β-MoTe2 samples. Upper inset shows temperature dependence ab-plane resistivity of Td-WTe2. Black symbols are the experimental data and the red line represents a fit with the Fermi liquid model  . (d) Composition-dependent of the ab-plane resistivities (I), carrier concentration (II) and mobility (III) of Mo1−xWxTe2 single crystals measured at room temperature. Green globules represent β-MoTe2 samples.
. (d) Composition-dependent of the ab-plane resistivities (I), carrier concentration (II) and mobility (III) of Mo1−xWxTe2 single crystals measured at room temperature. Green globules represent β-MoTe2 samples.

where ρ0 is the resistivity at 0 K and A is constant. It suggests that electrons in Td-WTe2 at low temperature can be well described by Landau Fermi liquid theory. The temperature dependent resistance of Td-WTe2 indeed shows a transition (T*) from linear behaviour originating from the electron-phonon coupling at high temperatures to the Landau Fermi liquid behaviour with dominant electron-electron scattering at low temperatures52. With the same method, we fitted the temperature-dependent resistivity of the other metallic phase samples. As shown in Fig. 6(c), it is found that upon raising the Mo concentration, T* of these samples gradually decreases, compared with Td-WTe2. And the T* of β-MoTe2 is 75 K. The calculation procedure of carrier concentrations and carrier mobilities is shown in Supplementary Information. Figure 6(d) summarized composition-dependent of the ab-plane resistivities (I), carrier concentration (II) and mobility (III) of Mo1−xWxTe2 single crystals measured at the room temperature. One can see, with increasing x, the ab-plane resistivity gradually decreases, the carrier concentration first increases and then rapidly decreases, while the mobility first decreases and then increases. Quantitatively, the ab-plane resistivities of 2H-MoTe2, β-MoTe2, and Td-WTe2 are 0.5, 1.0 × 10−3 and 3.4 × 10−4 Ω·cm, respectively. The carrier concentrations are 4.0 × 1017, 1.4 × 1021 and 3.0 × 1020 cm−3, respectively. And the mobilities are 32.2, 4.1, and 61.9 cm2V−1s−1, respectively.
Conclusions
In conclusion, we successfully synthesized a series of Mo1−xWxTe2 single crystals. By means of XRD, Raman spectroscopy, and DFT calculations, we find that by increasing the W composition (x), the structure gradually changes from 2H, β to type-II Weyl semimetal Td phase. By changing temperature, the high temperature β-phase of Mo1−xWxTe2 is evolved to low temperature Td-phase. Accordingly, temperature-dependent and composition-dependent phase diagram of Mo1−xWxTe2 is proposed. Simultaneously, the electrical property gradually evolves from semiconductor in 2H phase to semimetal β phase then to semimetal Td phase. This work provides a useful map to explore the type-II topological Weyl semimetal phase and temperature/composition-dependent topological phase transition, as well as the corresponding novel physical properties in Mo1−xWxTe2 compounds.
Additional Information
How to cite this article: Lv, Y.-Y. et al. Composition and temperature-dependent phase transition in miscible Mo1-xWxTe2 single crystals. Sci. Rep. 7, 44587; doi: 10.1038/srep44587 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Imai, H., Shimakawa, Y. & Kubo, Y. Large thermoelectric power factor in TiS2 crystal with nearly stoichiometric composition. Phys. Rev. B. 64, 241104(R) (2001).
Pan, X.-C. et al. Pressure-driven dome-shaped superconductivity and electronic structural evolution in tungsten ditelluride. Nat. Commun. 6, 7805 (2015).
Sipos, B. et al. From Mott state to superconductivity in 1T-TaS2 . Nat. Mater. 7, 960–965 (2008).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2 . Nature. 514, 205–208 (2014).
Qian, X. F., Liu, J. W., Fu, L. & Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science. 346, 1344–1347 (2014).
Ma, Y. D., Kou, L. Z., Li, X., Dai, Y. & Heine, T. Two-dimensional transition metal dichalcogenides with a hexagonal lattice: Room-temperature quantum spin Hall insulators. Phys. Rev. B. 93, 035442 (2016).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013).
Ho, C. H., Wu, C. S., Huangy, Y. S., Liao, P. C. & Tiong, K. K. Temperature dependence of energies and broadening parameters of the band-edge excitons of Mo1−x W x S2 single crystals. J. Phys.: Condens. Matter. 10, 9317–9328 (1998).
Chen, Y. F. et al. Tunable Band Gap Photoluminescence from Atomically Thin Transition-Metal Dichalcogenide Alloys. ACS Nano. 7, 4610–4616 (2013).
Tongay, S. et al. Two-dimensional semiconductor alloys: Monolayer Mo1−xWxSe2 . Appl. Phys. Lett. 104, 012101 (2014).
Ke, T. Y., Hsu, H. P., Wang, Y. P. & Huang, Y. S. Temperature dependent piezoreflectance study of Mo1−xWxSe2 layered crystals. J. Appl. Phys. 118, 215704 (2015).
Dawson, W. G. & Bullett, D. W. Electronic structure and crystallography of MoTe2 and WTe2 . J. Phys. C: Solid State Phys. 20, 6159–6174 (1987).
Ikeura, K., Sakai, H., Bahramy, M. S. & Ishiwata, S. Rich structural phase diagram and thermoelectric properties of layered tellurides Mo1−x Nb x Te2 . APL Mater. 3, 041514 (2015).
Hughes, H. P. & Friend, R. H. Electrical resistivity anomaly in β-MoTe2 . J. Phys. C: Solid State Phys. 11, L103–L105 (1978).
Zandt, T., Dwelk, H., Janowitz, C. & Manzke, R. J. Quadratic temperature dependence up to 50K of the resistivity of metallic MoTe2 . J. Alloys Compd. 442, 216–218 (2007).
Sun, Y., Wu, S.-C., Ali, M. N., Felser, C. & Yan, B. H. Prediction of Weyl semimetal in orthorhombic MoTe2 . Phys. Rev. B. 92, 161107(R) (2015).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature. 527, 495–498 (2015).
Weng, H. M., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X 5, 011029 (2015).
Xu, S. Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Lv, B. Q. et al. Observation of Weyl nodes in TaAs. Nat. Phys. 11, 724–727 (2015).
Huang, X. C. et al. Observation of the Chiral-Anomaly-Induced Negative Magnetoresistance in 3D Weyl Semimetal TaAs. Phys. Rev. X 5, 031023 (2015).
Bruno, F. Y. et al. Observation of large topologically trivial Fermi arcs in the candidate type-II Weyl semimetal WTe2 . Phys. Rev. B 94, 121112(R) (2016).
Wu, Y. et al. Observation of Fermi arcs in the type-II Weyl semimetal candidate WTe2 . Phys. Rev. B 94, 121113(R) (2016).
Deng, K. et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2 . Nat. Phys. 12, 1105–1110 (2016).
Huang, L. et al. Spectroscopic evidence for a type II Weyl semimetallic state in MoTe2 . Nat. Mater. 15, 1155–1160 (2016).
Wang, Y. J. et al. Gate-tunable negative longitudinal magnetoresistance in the predicted type-II Weyl semimetal WTe2 . Nat. Commun. 7, 13142 (2016).
Lv, Y.-Y. et al. Experimental observation of anisotropic Adler-Bell-Jackiw anomaly in type-II Weyl semimetal WTe1.98 crystals at the quasi-classical regime. arXiv:1608.05216 (2016).
Chang, T.-R. et al. Prediction of an arc-tunable Weyl Fermion metallicstate in Mo x W1−x Te2 . Nat. Commun. 7, 10639 (2016).
Belopolski, I. et al. Discovery of a new type of topological Weyl fermion semimetal state in Mo x W1−x Te2 . Nat. Commun. 7, 13643 (2016).
Clarke, R., Marseglia, E. & Hughes, H. P. A low-temperature structural phase transition in β-MoTe2 . Philosophical Magazine. 38, 121–126 (1978).
Wang, Z. J. et al. MoTe2: A Type-II Weyl Topological Metal. Phys. Rev. Lett. 117, 056805 (2016).
Joshi, J. et al. Phonon anharmonicity in bulk Td-MoTe2 . Appl. Phys. Lett. 109, 031903 (2016).
Zhang, K. N. et al. Raman signatures of inversion symmetry breaking and structural phase transition in type-II Weyl semimetal MoTe2. Nat. Commun. 7, 13552 (2016).
Duerloo, K.-A. N. & Reed, E. J. Structural Phase Transitions by Design in Monolayer Alloys. ACS Nano 10, 289–297 (2016).
Zhang, C. X. et al. Charge Mediated Reversible Metal-Insulator Transition in Monolayer MoTe2 and W x Mo1−x Te2 Alloy. ACS Nano 10, 7370–7375 (2016).
Revolinsky, E. & Beerntsen, D. Electrical Properties of the MoTe2-WTe2 and MoSe2-WSe2 Systems. J. Appl. Phys. 35, 2086–2089 (1964).
Champion, J. A. Some properties of (Mo, W) (Se, Te)2 . Brit. J. Appl. Phys., 16, 1035–1037 (1965).
Lv, Y.-Y. et al. Dramatically decreased magnetoresistance in nonstoichiometric WTe2 crystals. Scientific Reports. 6, 26903 (2016).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B. 48, 13115–13118 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B. 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 59, 1758–1775 (1999).
Klimes, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys.: Condens. Matter. 22, 022201 (2010).
Klimes, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B. 83, 195131 (2011).
Shannon, R. D. Revised Effective Ionic Radii and Systematic Studies of Interatomie Distances in Halides and Chaleogenides. Acta Cryst. A32, 751–767 (1976).
Yamamoto, M. et al. Strong Enhancement of Raman Scattering from a Bulk-Inactive Vibrational Mode in Few-Layer MoTe2 . ACS Nano. 4, 3895–3903 (2014).
Keum, D. H. et al. Bandgap opening in few-layered monoclinic MoTe2 . Nat. Phys. 11, 482–486 (2015).
Kong, W.-D. et al. Raman scattering investigation of large positive magnetoresistance material WTe2 . Appl. Phys. Lett. 106, 081906 (2015).
Chakraborty, B. et al. Symmetry-dependent phonon renormalization in monolayer MoS2 transistor. Phys. Rev. B 85, 161403(R) (2012).
Drew, H. D. & Strom, U. Electron Relaxation Rates in Bismuth at Microwave and Far-Infrared Frequencies. Phys. Rev. Lett. 25, 1755–1758 (1970).
Acknowledgements
We’d like to acknowledge the financial support from the National Basic Research Program of China (973 Program) (2015CB921203 and 2013CB632702), the National Natural Science Foundation of China (51032003, 51472112, 11374149, 91622122, 11474150 and 10974083), and the Program for New Century Excellent Talents in University (NCET-09-0451). Y.-Y.L. acknowledges the financial support from the Graduate Innovation Fund of Nanjing University (2015CL11). We also acknowledge the support for the computational resources by the High Performance Computing Center of Nanjing University.
Author information
Authors and Affiliations
Contributions
S.-H.Y. and Y.-Y.L. performed the crystal growth in assist of D.-J.L. and B.P. Y.-Y.L., C.L., K.W. and L.G.M. did the EDS analyses, XRD measurements and Raman spectra of the crystals. Y.-Y.L., X.L. and B.-B.Z. conducted the transport measurements. S.-H.Y., J.Z. and Y.-Y.L analyzed the data and refined the measurements. Y.-B.C., Y.-F.C. and Y.L.C. contributed to the result analysis. J.Z. did the density functional theory calculations. Y.-Y.L., S.-H.Y. and J.Z. co-wrote the manuscript. M.-H.L., Y.-B.C., W.C.L. and S.-T.D. revised the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Lv, YY., Cao, L., Li, X. et al. Composition and temperature-dependent phase transition in miscible Mo1−xWxTe2 single crystals. Sci Rep 7, 44587 (2017). https://doi.org/10.1038/srep44587
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep44587
This article is cited by
-
Sub-picosecond photo-induced displacive phase transition in two-dimensional MoTe2
npj 2D Materials and Applications (2020)
-
Electric-field induced structural transition in vertical MoTe2- and Mo1–xWxTe2-based resistive memories
Nature Materials (2019)
-
Realization of vertical metal semiconductor heterostructures via solution phase epitaxy
Nature Communications (2018)
-
Structural characterizations and electrical conduction mechanism of CaBi2Nb2O9 single-phase nanocrystallites synthesized via sucrose-assisted sol–gel combustion method
Journal of Materials Science (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.