Abstract
Two-dimensional (2D) materials and their corresponding van der Waals heterostructures have drawn tremendous interest due to their extraordinary electrical and optoelectronic properties. Insulating 2D hexagonal boron nitride (h-BN) with an atomically smooth surface has been widely used as a passivation layer to improve carrier transport for other 2D materials, especially for Transition Metal Dichalcogenides (TMDCs). However, heat flow at the interface between TMDCs and h-BN, which will play an important role in thermal management of various electronic and optoelectronic devices, is not yet understood. In this paper, for the first time, the interface thermal conductance (G) at the MoS2/h-BN interface is measured by Raman spectroscopy, and the room-temperature value is (17.0 ± 0.4) MW · m−2K−1. For comparison, G between graphene and h-BN is also measured, with a value of (52.2 ± 2.1) MW · m−2K−1. Non-equilibrium Green’s function (NEGF) calculations, from which the phonon transmission spectrum can be obtained, show that the lower G at the MoS2/h-BN interface is due to the weaker cross-plane transmission of phonon modes compared to graphene/h-BN. This study demonstrates that the MoS2/h-BN interface limits cross-plane heat dissipation, and thereby could impact the design and applications of 2D devices while considering critical thermal management.
Similar content being viewed by others
Introduction
Two-dimensional (2D) materials with atomic-scale thickness have drawn tremendous interest since the successful exfoliation of graphene1. Although graphene has a unique electronic bandstructure, which has led to interesting phenomena like massless Dirac fermion physics2,3,4 and anomalous quantum Hall effect5,6,7, its zero-bandgap makes it unsuitable for use as field effect transistors (FETs), despite some recent attempts to open a bandgap in graphene8,9,10,11,12. Transition metal dichalcogenides (TMDCs), including the semiconducting MX2 (M = Mo, W; X = S, Se, Te), on the other hand, have electronic bandgaps covering the visible region13. What is more interesting is that the bandgaps of TMDCs are thickness-dependent14. For instance, molybdenum disulfide (MoS2) has a bandgap ranging from 1.3 eV to 1.9 eV as the number of layers increases from single to bulk15. Hexagonal boron nitride (h-BN) is a good 2D insulator with a bandgap of 5.971 eV16. Because of its atomically smooth surface and dielectric nature, h-BN is widely used as a high quality substrate for graphene17,18 and TMDCs19,20,21. For MoS2 supported by h-BN, the carrier mobility increases by more than an order of magnitude compared to that of SiO2 supported MoS2, because h-BN effectively protects the MoS2 channel from Coulomb scattering by charged impurities in SiO221, similar to what is observed for graphene FETs on h-BN17.
Compared to the numerous studies13,14,22,23,24,25,26,27 on the electronic and optoelectronic properties of 2D materials and the van der Waals heterostructures mentioned above, there is a paucity of research on their thermal properties in spite of their relevance to heat management, which is critical for maintaining optimal functionality of these devices14,28,29,30. In general, most thermal studies focus on the suspended configuration where the 2D material is isolated from a substrate to exclude the contribution from the substrate31,32,33,34,35. Although such measurements further our understanding of phonon interactions within the 2D system, they are of limited relevance to realistic device applications for which the supported configuration is more practical. The thermal properties of this supported configuration are still not well studied, and there are only few works reported on graphene36,37,38,39 and MoS240,41 on various bulk substrates. TMDC flakes situated on another 2D material such as h-BN being the substrate, i.e., two 2D-material interface/heterostructure, is far less investigated, which is in great demand in the emerging heterostructures and optoelectronic devices involving stacked 2D materials. Compared to the suspended configuration where heat transport only occurs in the basal plane, the difficulty with the supported configuration comes from the three-dimensional (3D) nature of heat transport. Even though the in-plane thermal conductivities of the two materials involved could be obtained individually by suspending each sample across a measurement platform, the thermal conductivity changes when the samples are supported due to the suppression of the flexural mode phonons and interactions between the substrate and superstrate36,37,42. In order to deconvolve such a 3D problem, it is critical to know the interface thermal conductance.
Finite interface thermal conductance (G) was first observed by Kapitza at the copper and liquid helium boundary43, and was later explained by the acoustic mismatch model (AMM)44, which assumes that phonons reaching the interface undergo specular reflection or transmission following continuum mechanics for a perfectly smooth interface. However, subsequent experiments have shown that the AMM breaks down for phonons with frequency larger than 100 GHz45, therefore leading to the development of the diffuse mismatch model (DMM) for thermal phonons46. The DMM assumes that the transmission of phonons reaching the interface depends on the ratio of the phonon density of states of either side46. With the DMM, Reddy et al. calculated G for metal-semiconductor interfaces such as Al/Si, Al/Ge, Cu/Si and Cu/Ge using exact phonon dispersions47. Lyeo et al. measured G for an assembly of dissimilar materials using time-domain thermoreflectance (TDTR), exploring the lower bounds of G and found that such a lower bound actually lies within a narrow range of 8 to 30 MW/m2K48.
For supported 2D materials, although heat is dissipated predominantly in the vertical direction as compared to laterally49, the study of the vertical interface conductance, G, has just recently expanded to the regime of 2D materials. By Joule/optical heating graphene and measuring temperatures via Raman spectroscopy, Yue et al. measured G between epitaxial graphene and 4H-SiC to be 0.0189 MW/m2K, which is five orders of magnitude lower than that expected from their molecular dynamics (MD) simulations50. They attributed the much lower measured G to the significantly enhanced phonon scattering effect from the structural change at the interface caused by 1) the high stress induced by covalent bonds between graphene/SiC and 2) the thermal expansion mismatch caused by separation at the interface. With a similar technique, Chen et al. measured G between graphene and h-BN to be 7.4 MW/m2K51. Similarly, this result is still more than an order of magnitude smaller than the theoretically predicted value of 187 MW/m2K52, and is explained as a result of random lattice-mismatch and possible contaminations at the interface51. For MoS2, Taube et al. measured the total G across MoS2/Si including a thin SiO2 layer to be 1.94 MW/m2K41, and Zhang et al. measured G to be 0.44 MW/m2K for MoS2/Au40. These results were obtained by solving the heat diffusion equation based on the temperatures obtained from Raman spectroscopy, and the thermal conductivity was obtained simultaneously. However, this method requires the precise determination of absorbed laser power, to which interface thermal conductance and the thermal conductivity are sensitive.
In this work, we directly measure and compare G between MoS2/h-BN and graphene/h-BN, borrowing the technique from the work of Yue et al.50 and Chen et al.51, while paying special attention to the interface quality. Specifically, we increase the temperature of the top MoS2 (graphene) through Joule heating, and at the same time, monitor the temperatures of MoS2 (graphene) and h-BN via Raman spectroscopy. The thermal conductance across the MoS2 and h-BN interface is (17.0 ± 0.4) MW/m2K, which is ~3 times smaller than G for graphene/h-BN interface measured as (52.2 ± 2.1) MW/m2K. With the expected lower in-plane thermal conductivity of MoS2 compared to graphene, this could indicate that electronic and optoelectronic devices using MoS2/h-BN have a larger propensity for failure due to overheating and therefore this value needs to be considered carefully in the future design of such devices.
To understand further the physics behind this difference in G, we conduct non-equilibrium Green’s function (NEGF) calculations of these two interfaces, which show a trend consistent with experiments. Our simulation consists of a semi-infinite superstrate of graphene or MoS2 sheets and a semi-infinite substrate of h-BN sheets. The graphene layers are stacked in the A-B configuration while the h-BN and MoS2 are stacked in the A-A’ configuration. In each structure, the interfacial area is 2.49 × 2.2 nm2. The interatomic potentials are obtained from literature53,54,55. After optimizing the structures in GULP56, we compute their force constant matrices and input them into our NEGF code to calculate the transmission spectrum across the interface. The interface thermal conductance G is obtained using the formula

where Gint, Gsuper and Gsub are respectively the conductance of the MoS2/h-BN (or graphene/h-BN), MoS2/MoS2 (or graphene/graphene) and h-BN/h-BN interfaces.
Results
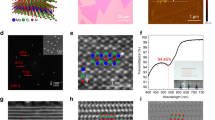
The fabricated MoS2/h-BN FET device is shown in Fig. 1(a). The Raman spectra of MoS2 and h-BN are shown in Fig. 1(c) and (d). The photoluminescence (PL) of MoS2 is shown in Fig. 1(b). The distance between the MoS2 E′ peak and the  peak (~18 cm−1)57, and the location of the PL peak at 1.84 eV indicate that our sample is indeed monolayer MoS215. The four electrodes are patterned in order to probe the electrical contact resistance (Rc) between MoS2 and the two inner electrodes, which are used for Joule heating.
peak (~18 cm−1)57, and the location of the PL peak at 1.84 eV indicate that our sample is indeed monolayer MoS215. The four electrodes are patterned in order to probe the electrical contact resistance (Rc) between MoS2 and the two inner electrodes, which are used for Joule heating.
(a) Optical image of the MoS2/h-BN heterostructure. Dashed box indicates MoS2. (b) Photoluminescence and (c) Raman bands of MoS2. The PL location at 1.84 eV and the distance between the E′ and the band (~18 cm−1) indicates that it is indeed monolayer MoS2. (d) Raman E2g band indicating the high quality of h-BN.
band (~18 cm−1) indicates that it is indeed monolayer MoS2. (d) Raman E2g band indicating the high quality of h-BN.
To determine G, it is necessary to know the temperatures of the MoS2 and h-BN. Raman spectroscopy has been demonstrated to be an effective method to probe the temperatures of 2D materials31,33,34,37,40,41,58, based on the fact that the Raman spectra red-shifts as temperature rises due to lattice softening and anharmonic scattering of phonons. To measure temperatures with Raman spectroscopy, the experiment is divided into two parts. The first part is the calibration of the Raman shifts for MoS2 and h-BN as a function of temperature. At this stage, the temperatures of the materials are externally controlled via a heater stage, and their corresponding Raman spectra are collected at each temperature point. This calibration ensures that the temperature of each material can be determined by referring to their Raman spectra in the subsequent Joule heating measurement. Next, a series of current bias are applied to the electrically conducting MoS2 to provide Joule heat power given by Po = I2R (where I is the drain source current and R is the electrical resistance of MoS2 including contact resistance Rc). The laser spot is located in the middle of the sample. Note here that the relaxation time for electron-phonon interaction is on a short time scale of picoseconds with a relaxation length of the order of nanometers59, while our measurements are in steady state for a sample size of several microns, and thus there should be no discrepancy between Joule heating and global cryostat heating. The generated heat is dissipated in the cross-plane direction and heats up the underlying h-BN, while the sample stage is maintained at room temperature. All measurements are performed in a high vacuum environment in a closed-cycle cryostat (<10−5 torr). The Raman spectra of MoS2 and h-BN are monitored at each current bias to determine their temperatures based on the calibration results in the first part of measurement.
The temperature calibration of the Raman spectra of MoS2 and h-BN are shown in Fig. 2(a). For MoS2, the in-plane E′ mode is sensitive to strain, while the out-of-plane  mode is not60,61. Thus, the
mode is not60,61. Thus, the  peak is chosen as the temperature indicator for MoS2 to avoid interference from strain-induced Raman shifts. The relationship between the Raman shift and the temperature can be expressed as
peak is chosen as the temperature indicator for MoS2 to avoid interference from strain-induced Raman shifts. The relationship between the Raman shift and the temperature can be expressed as  , where Δω is the Raman shift due to temperature change, χT is the first-order temperature coefficient, and ΔT is the temperature change. The χT for the MoS2
, where Δω is the Raman shift due to temperature change, χT is the first-order temperature coefficient, and ΔT is the temperature change. The χT for the MoS2  peak and h-BN are measured to be 0.01212 cm−1 · K−1 and 0.01723 cm−1·K−1 for the first sample, and 0.01243 cm−1 · K−1 and 0.01778 cm−1 · K−1 for the second sample, respectively.
peak and h-BN are measured to be 0.01212 cm−1 · K−1 and 0.01723 cm−1·K−1 for the first sample, and 0.01243 cm−1 · K−1 and 0.01778 cm−1 · K−1 for the second sample, respectively.
During the MoS2 Joule heating process, the temperatures of the MoS2 and the underlying h-BN increase, resulting in red shifts of thr Raman peaks as indicated in Fig. 2(b). The Joule heating power coefficient χP, which is defined as  , is measured to be 0.10123 cm−1 · mW−1 and 0.12697 cm−1 · mW−1 for the MoS2
, is measured to be 0.10123 cm−1 · mW−1 and 0.12697 cm−1 · mW−1 for the MoS2  peak and h-BN for the first sample, and 0.09972 cm−1 · mW−1 and 0.12719 cm−1 · mW−1 for the MoS2
peak and h-BN for the first sample, and 0.09972 cm−1 · mW−1 and 0.12719 cm−1 · mW−1 for the MoS2  . peak and h-BN for the second sample.
. peak and h-BN for the second sample.
The interface thermal conductance between MoS2 and h-BN is calculated from

where ΔT is the temperature difference beten MoS2 and h-BN.

is the heat flux across the interface. Here, A is the interface area (including the transfer lengths from contacts) between MoS2 and h-BN, which is 50.50 μm2 and 73.05 μm2 for the two samples we measured. PO = P + Pc is the total Joule heating power, including both the power P from the MoS2 channel and Pc from the contact resistance Rc between MoS2 and the two inner electrodes used for Joule heating. Pc is determined through a 2-probe/4-probe resistance measurement, and  and
and  for the two samples is found (Supplementary Information). ΔT can be obtained based on the Raman measurements described above, i.e.,
for the two samples is found (Supplementary Information). ΔT can be obtained based on the Raman measurements described above, i.e.,

Combining (1) and (2), the interface thermal conductance G is calculated to be 20.1 MW · m−2K−1 and 15.8 MW · m−2K−1 for the two samples.
To improve the accuracy of our measured G, we also consider the non-uniform heat flux within the basal plane of MoS2 and the influence from the contact resistance. A three-dimensional finite element method (3D FEM) using COMSOL is used to estimate the local (center of the sample) heat flux. This is realized by treating G as an input parameter and iteratively making it consistent with the local temperature difference observed from experiments (Supplementary information). The G for these two samples after local heat flux correction is 17.3 MW · m−2K−1 and 16.7 MW · m−2K−1. By averaging the values of G from the two samples after 3D FEM correction, we obtain the effective interface thermal conductance between MoS2 and h-BN of (17.0 ± 0.4) MW · m−2K−1. The G obtained for MoS2/h-BN interface here is larger than that of the MoS2/Au interface which has a value of 0.44 MW · m−2K−1 40. This is possibly because of the ultra-smooth h-BN surface and/or better thermal coupling between MoS2 and h-BN intrinsically.
To obtain a better understanding of thermal conductance across such van der Waals interfaces, we also measure G for the graphene/h-BN interface for comparison. Similarly, the measurement is composed of two parts, that is, the Raman shift calibration against temperature and the Joule heating measurement. The measurement results for the two parts are shown in Fig. 3. For the graphene/h-BN interface, with an interface area of 43.55 μm2 and  , the thermal conductance is extracted to be 45.1 MW · m−2K−1 and 47.8 MW · m−2K−1 based on the graphene Raman G band and 2D band respectively. Similar to the MoS2/h-BN case, the local heat flux correction from 3D FEM COMSOL simulation gives 53.7 MW · m−2K−1 and 50.7 MW · m−2K−1 based on the graphene Raman G band and 2D band respectively, resulting in an average effective value of (52.2 ± 2.1) MW · m−2K−1. When observing the heterostructures with AFM, we find bubbles of size ~100 nm randomly dispersed within the interfaces of both MoS2/h-BN and graphene/h-BN (Supplementary information). These bubbles are almost unavoidable during the transfer process, and difficult to remove completely even after annealing. It has been shown that these bubbles could be formed by chemical adsorbates on crystals used for preparing the heterostructures in ambient conditions, and the trapped materials could be amorphous hydrocarbons62. Depending on the thermal conductance of the bubbles: if bubbles have a smaller/larger G than the intrinsic G between MoS2/h-BN, our measurement results represents the lower/upper bounds of G. Bubble-free 2D heterostructures could be accessible with fabrication processes performed in a vacuum environment, which deserves further studies.
, the thermal conductance is extracted to be 45.1 MW · m−2K−1 and 47.8 MW · m−2K−1 based on the graphene Raman G band and 2D band respectively. Similar to the MoS2/h-BN case, the local heat flux correction from 3D FEM COMSOL simulation gives 53.7 MW · m−2K−1 and 50.7 MW · m−2K−1 based on the graphene Raman G band and 2D band respectively, resulting in an average effective value of (52.2 ± 2.1) MW · m−2K−1. When observing the heterostructures with AFM, we find bubbles of size ~100 nm randomly dispersed within the interfaces of both MoS2/h-BN and graphene/h-BN (Supplementary information). These bubbles are almost unavoidable during the transfer process, and difficult to remove completely even after annealing. It has been shown that these bubbles could be formed by chemical adsorbates on crystals used for preparing the heterostructures in ambient conditions, and the trapped materials could be amorphous hydrocarbons62. Depending on the thermal conductance of the bubbles: if bubbles have a smaller/larger G than the intrinsic G between MoS2/h-BN, our measurement results represents the lower/upper bounds of G. Bubble-free 2D heterostructures could be accessible with fabrication processes performed in a vacuum environment, which deserves further studies.
Compared with the G of 7.4 MW · m−2K−1 measured in Chen et al.51, our observed higher G for the graphene/h-BN interface is due to the higher quality of the interfaces. Our G for the graphene/h-BN interface is also much higher than that of the graphene/SiC interface (0.0187 MW · m−2K−1)50. This is possibly due to less strain in the graphene superstrate when it is van der Waals coupled with h-BN than when it is covalent bonded to SiC, as tensile strain in graphene during the heating process tends to increase the red-shift of Raman peaks, resulting in the overestimation of the temperature of graphene and thereby underestimates G.
Compared with the MoS2/h-BN interface, graphene/h-BN has a better interface thermal conductance. To better understand the physics behind this difference, we employ the NEGF technique to calculate the thermal conductance and transmittance spectrum. Figure 4 shows the temperature dependence of the thermal conductance and transmittance spectrum for the MoS2/h-BN and the graphene/h-BN interfaces. Our measurement results of G (17.0 ± 0.4) is close to that from NEGF calculation of 26.4 MW · m−2K−1, which serves as the theoretical upper bound of this interface, indicating the high quality of our interface. The measured G for the graphene/h-BN (52.2 ± 2.1) MW · m−2K−1 is larger than that for MoS2/h-BN, the same trend as predicted by NEGF calculations. From the phonon transmittance spectrum across the interfaces [Fig. 4(b) and (c)], it can be observed that the lower G across the MoS2/h-BN interface is due to the lower phonon transmittance of MoS2, which has a much smaller overlap with the h-BN transmittance spectrum and thus, a smaller effective transmittance spectrum for the interface, as compared to the graphene/h-BN case. Thus, the much lower thermal conductance for the MoS2/h-BN interface is due to the phonon transmission bottleneck caused by the limited number of transmission channels in MoS2, compared to the greater number of transmission channels in graphene.
(a) Temperature dependence of the thermal conductance of the MoS2/h-BN and the graphene/h-BN interface. (b) and (c) show the schematic of the atomistic structure of the interface and its transmittance spectrum along with the spectra of the superstrate and the substrate for the MoS2/h-BN and the graphene/h-BN interfaces, respectively. The transmittance per unit area indicates the number of phonons transmitted across the interface per unit area.
Although G for graphene/h-BN interface is larger than that of the MoS2/h-BN interface, it is still much smaller than the NEGF-calculated values. This may be due to tensile strain originating from thermal expansion in graphene, which tends to increase the Raman peak red-shift63,64,65 during the Joule heating process, thus overestimating the temperature of graphene, and finally underestimating G based on eq. (1). It is worth noting that this effect of strain does not affect significantly the measurement of the MoS2/h-BN interface, as we intentionally chose the strain-insensitive  mode of MoS2 as the temperature indicator. Therefore, we observed G for the MoS2/h-BN interface to be closer to theoretical predictions. Another explanation for the discrepancy is the dependence of G on the number of layers which has been shown in molecular dynamics simulations66 to be lower for a single-layer crystal than for a multilayer crystal. Hence, it is expected that the interface thermal conductance for multilayer structures should be significantly higher than for single-layer 2D crystals. Our measured G values are for temperatures higher than 300 K (the stage is kept at 300 K while the top MoS2 or graphene is Joule heated with the temperature higher than 300 K), and G should be temperature-independent above this temperature, based on NEGF calculations (Fig. 4). For the MoS2/h-BN interface in particular, heat is dissipated primarily via the low-frequency (sub-70 cm−1) modes whose contributions to the conductance are temperature-independent when T ≫ 100 K.
mode of MoS2 as the temperature indicator. Therefore, we observed G for the MoS2/h-BN interface to be closer to theoretical predictions. Another explanation for the discrepancy is the dependence of G on the number of layers which has been shown in molecular dynamics simulations66 to be lower for a single-layer crystal than for a multilayer crystal. Hence, it is expected that the interface thermal conductance for multilayer structures should be significantly higher than for single-layer 2D crystals. Our measured G values are for temperatures higher than 300 K (the stage is kept at 300 K while the top MoS2 or graphene is Joule heated with the temperature higher than 300 K), and G should be temperature-independent above this temperature, based on NEGF calculations (Fig. 4). For the MoS2/h-BN interface in particular, heat is dissipated primarily via the low-frequency (sub-70 cm−1) modes whose contributions to the conductance are temperature-independent when T ≫ 100 K.
Discussion
In summary, we have measured the thermal conductance across the interface of 2D MoS2/h-BN and graphene/h-BN heterostructures. This is realized by Joule heating the MoS2 (graphene) superstrate, and monitoring the temperatures of both the superstrate MoS2 (graphene) and h-BN substrate through Raman spectroscopy. The measured thermal conductance of MoS2/h-BN interface is (17.0 ± 0.4) MW · m−2K−1, which is smaller than the value of graphene/h-BN interface (52.2 ± 2.1) MW · m−2K−1, consistent with the trend predicted from our NEGF calculations. We attribute the lower thermal conductance across the MoS2/h-BN interface to the limited cross-plane phonon transmission in MoS2, when compared to graphene. Our measurements and calculations provide basis for the study of in-plane thermal conductivity of MoS2 supported by h-BN, the typical structure for building high-mobility TMDC FET devices. The low interface thermal conductance deserves careful consideration for the design of electronic and optoelectronic devices based on such heterostructures.
Methods
The MoS2 flake was exfoliated onto a 285 nm SiO2/Si substrate, and was confirmed to be monolayer from its Raman distance between the E′ and  peaks (~18 cm−1) photoluminescence peak (~1.84 eV) (Fig. 1). The h-BN flake was exfoliated onto another 285 nm SiO2/Si substrate. The MoS2 was then transferred onto the h-BN with polymethyl methacrylate (PMMA) as an assisted layer followed by acetone etching. The electrodes were patterned by standard electron-beam lithography (EBL) process, followed with thermal evaporation of Ti/Au with thickness of 5 nm and 75 nm, respectively. The sample was then annealed in-situ in vacuum at 400 K for 6 hours to release strains produced during the transfer process and ensure that the two materials are fully adhered67. The graphene/h-BN heterostructure was prepared following the same procedure.
peaks (~18 cm−1) photoluminescence peak (~1.84 eV) (Fig. 1). The h-BN flake was exfoliated onto another 285 nm SiO2/Si substrate. The MoS2 was then transferred onto the h-BN with polymethyl methacrylate (PMMA) as an assisted layer followed by acetone etching. The electrodes were patterned by standard electron-beam lithography (EBL) process, followed with thermal evaporation of Ti/Au with thickness of 5 nm and 75 nm, respectively. The sample was then annealed in-situ in vacuum at 400 K for 6 hours to release strains produced during the transfer process and ensure that the two materials are fully adhered67. The graphene/h-BN heterostructure was prepared following the same procedure.
After measurements, the interface quality was characterized with AFM. For MoS2/h-BN, bubbles of the size of ~100 nm were found at the interface. We found that these bubbles are almost unavoidable during the transfer process and difficult to remove once formed. Generally, high temperature annealing (350 °C) tends to make small bubbles from larger ones for graphene/h-BN62. Therefore, we annealed the graphene/h-BN samples in Ar atmosphere at 350 °C for 3.5 hours, and specifically chose areas with fewer bubbles for device fabrication. For those regions without bubbles, we found the roughness of the surface, which is defined as the root mean square average of height deviations taken from the mean image data plane, is ~1.5 nm, with the main contribution from polymeric residues during the transfer process. These polymeric residues are on the top surface of MoS2, thus won’t affect the interface. We find no obvious difference in roughness for the surface of h-BN and the region of MoS2 without bubbles, indicating the good conformity of the interface.
Additional Information
How to cite this article: Liu, Y. et al. Thermal Conductance of the 2D MoS2/h-BN and graphene/h-BN Interfaces. Sci. Rep. 7, 43886; doi: 10.1038/srep43886 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., Grigorieva, I. V. & Firsov, A. A. Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666–669 (2004).
Huard, B. et al. Transport measurements across a tunable potential barrier in graphene. Phys. Rev. Lett. 98, 236803 (2007).
Katsnelson, M. I., Novoselov, K. S. & Geim, A. K. Chirial tunnelling and the Klein paradox in graphene. Nat. Phys. 2, 620–625 (2006).
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nat. Mater. 6, 183–191 (2007).
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).
Zhang, Y., Tan, Y. W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).
Novoselov, K. S. et al. Unconventional quantum Hall effect and Berry’s phase of 2pi in bilayer graphene. Nat. Phys. 2, 177–180 (2006).
Li, X., Wang, X., Zhang, L., Lee, S. & Dai, H. Chemically derived, ultrasmooth graphene nanoribbon semiconductors. Science 319, 1229–1232 (2008).
Xia, F., Farmer, D. B., Lin, Y. M. & Avouris, P. Graphene field-effect transistors with high on/off current ratio and large transport band gap at room temperature. Nano Lett. 10, 715–718 (2010).
Zhang, Y. et al. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 459, 820–823 (2009).
Obradovic, B. et al. Analysis of graphene nanoribbons as a channel material for field-effect transistors. Appl. Phys. Lett. 88, 142102 (2006).
Han, M. Y., Özyilmaz, B., Zhang, Y. & Kim, P. Energy band-gap engineering of graphene nanoribbons. Phys. Rev. Lett. 98, 206805 (2007).
Xia, F., Wang, H., Xiao, D., Dubey, M. & Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photonics 8, 899–907 (2014).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Watanabe, K., Taniguchi, T. & Kanda, H. Direct-bandgap properties and evidence for ultraviolet lasing of hexagonal boron nitride single crystal. Nat. Mater. 3, 404–409 (2004).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722–726 (2010).
Dean, C. R. et al. Multicomponent fractional quantum Hall effect in graphene. Nat. Phys. 7, 693–696 (2011).
Cui, X. et al. Multi-terminal transport measurements of MoS2 using a van der Waals heterostructure device platform. Nat. Nanotechnol. 10, 534–540 (2015).
Chan, M. Y. et al. Suppression of thermally activated carrier transport in atomically thin MoS2 on crystalline hexagonal boron nitride substrates. Nanoscale 5, 9572–9576 (2013).
Lee, G.-H. et al. Flexible and Transparent MoS2 Field-Effect Transistors on Hexagonal Boron Nitride-Graphene Heterostructures. ACS Nano 7, 7931–7936 (2013).
Sun, Z. & Chang, H. Graphene and Graphene-like Two-Dimensional Materials in Photodetection: Mechanisms and Methodology. ACS Nano 8, 4133–4156 (2014).
Withers, F. et al. Light-emitting Diodes by Band-structure Engineering in van der Waals Heterostructures. Nat. Mater. 14, 301–306 (2015).
Pospischil, A. & Mueller, T. Optoelectronic Devices Based on Atomically Thin Transition Metal Dichalcogenides. Appl. Sci. 6, 78 (2016).
Koppens, F. H. L. et al. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 9, 780–793 (2014).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 10, 216–226 (2016).
Eda, G. & Maier, S. A. Two-Dimensional Crystals : Managing Light for Optoelectronics. ACS Nano 7, 5660–5665 (2013).
Freitag, M. et al. Energy dissipation in graphene field-effect transistors. Nano Lett. 9, 1883–1888 (2009).
Cahill, D. G. et al. Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 1, 11305 (2014).
Fiori, G. et al. Electronics based on two-dimensional materials. Nat. Nanotechnol. 9, 768–779 (2014).
Balandin, A. A. et al. Superior thermal conductivity of single-layer graphene. Nano Lett. 8, 902–907 (2008).
Xu, X. et al. Length-dependent thermal conductivity in suspended single-layer graphene. Nat. Commun. 5, 3689 (2014).
Sahoo, S., Gaur, A. P. S., Ahmadi, M., Guinel, M. J.-F. & Katiyar, R. S. Temperature-dependent Raman studies and thermal conductivity of few-layer MoS2 . J. Phys. Chem. C 117, 9042–9047 (2013).
Peimyoo, N. et al. Thermal conductivity determination of suspended mono- and bilayer WS2 by Raman spectroscopy. Nano Res. 8, 1210–1221 (2015).
Ghosh, S. et al. Dimensional crossover of thermal transport in few-layer graphene. Nat. Mater. 9, 555–558 (2010).
Wang, Z. et al. Thermal transport in suspended and supported few-layer graphene. Nano Lett. 11, 113–118 (2011).
Cai, W. et al. Thermal transport in suspended and supported monolayer graphene grown by chemical vapor deposition. Nano Lett. 10, 1645–1651 (2010).
Mak, K. F., Lui, C. H. & Heinz, T. F. Measurement of the thermal conductance of the graphene/SiO2 interface. Appl. Phys. Lett. 97, 221904 (2010).
Huang, B. & Koh, Y. K. Improved topological conformity enhances heat conduction across metal contacts on transferred graphene. Carbon. 105, 268–274 (2016).
Zhang, X. et al. Measurement of Lateral and Interfacial Thermal Conductivity of Single- and Bilayer MoS2 and MoSe2 Using Refined Optothermal Raman Technique. ACS Appl. Mater. Interfaces 7, 25923–25929 (2015).
Taube, A., Judek, J., Łapińska, A. & Zdrojek, M. Temperature-dependent thermal properties of supported MoS2 monolayers. ACS Appl. Mater. Interfaces 7, 5061–5065 (2015).
Seol, J. H. et al. Two-Dimensional Phonon Transport in Supported Graphene. Science 328, 213–216 (2010).
Kapitza, P. L. Investigation of the mechanism of heat conduction in helium II. J. phys 4, 181–280 (1941).
Little, W. A. The Transport of Heat between Dissimilar Solids at Low temperatures. Can. J. Phys. 37, 334–349 (1959).
Eisenmenger, W. Phonon scattering at surfaces and interfaces. Phonon Scatt. Condens. Matter V 204–211 (1986).
Swartz, E. T. & Pohl, R. O. Thermal boundary resistance. Rev. Mod. Phys. 61, 605–668 (1989).
Reddy, P., Castelino, K. & Majumdar, A. Diffuse mismatch model of thermal boundary conductance using exact phonon dispersion. Appl. Phys. Lett. 87, 211908 (2005).
Lyeo, H.-K. K. & Cahill, D. G. Thermal conductance of interfaces between highly dissimilar materials. Phys. Rev. B 73, 144301 (2006).
Jo, I. et al. Low-frequency acoustic phonon temperature distribution in electrically biased graphene. Nano Lett. 11, 85–90 (2011).
Yue, Y., Zhang, J. & Wang, X. Micro/nanoscale spatial resolution temperature probing for the interfacial thermal characterization of epitaxial graphene on 4H-SiC. Small 7, 3324–3333 (2011).
Chen, C. C., Li, Z., Shi, L. & Cronin, S. B. Thermal interface conductance across a graphene/hexagonal boron nitride heterojunction. Appl. Phys. Lett. 104, 81908 (2014).
Mao, R. et al. Phonon engineering in nanostructures: Controlling interfacial thermal resistance in multilayer-graphene/dielectric heterojunctions. Appl. Phys. Lett. 101, 113111 (2012).
Ding, Z., Jiang, J.-W., Pei, Q.-X. & Zhang, Y.-W. In-plane and cross-plane thermal conductivities of molybdenum disulfide. Nanotechnology 26, 65703 (2015).
Kınacı, A., Haskins, J. B., Sevik, C. & ÇağIn, T. Thermal conductivity of BN-C nanostructures. Phys. Rev. B 86, 115410 (2012).
Ye, Z., Otero-de-la-Roza, A., Johnson, E. R. & Martini, A. Oscillatory motion in layered materials: graphene, boron nitride, and molybdenum disulfide. Nanotechnology 26, 165701 (2015).
Gale, J. D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc., Faraday Trans. 93, 629–637 (1997).
Chen, S. Y., Zheng, C., Fuhrer, M. S. & Yan, J. Helicity-Resolved Raman Scattering of MoS2, MoSe2, WS2, and WSe2 Atomic Layers. Nano Lett. 15, 2526–2532 (2015).
Yan, R. et al. Thermal conductivity of monolayer molybdenum disulfide obtained from temperature-dependent Raman spectroscopy. ACS Nano 8, 986–993 (2014).
Pop, E., Sinha, S. & Goodson, K. E. Heat generation and transport in nanometer-scale transistors. Proc. IEEE 94, 1587–1601 (2006).
Rice, C. et al. Raman-scattering measurements and first-principles calculations of strain-induced phonon shifts in monolayer MoS2 . Phys. Rev. B 87, 81307 (2013).
Wang, Y., Cong, C., Qiu, C. & Yu, T. Raman spectroscopy study of lattice vibration and crystallographic orientation of monolayer MoS2 under uniaxial strain. Small 9, 2857–2861 (2013).
Haigh, S. J. et al. Cross-sectional imaging of individual layers and buried interfaces of graphene-based heterostructures and superlattices. Nat. Mater. 11, 764–767 (2012).
Huang, M., Yan, H., Heinz, T. F. & Hone, J. Probing strain-induced electronic structure change in graphene by Raman spectroscopy. Nano Lett. 10, 4074–4079 (2010).
Ni, Z. H. et al. Uniaxial strain on graphene: Raman spectroscopy study and band-gap opening. ACS Nano 2, 2301–2305 (2008).
Mohiuddin, T. M. G. et al. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Gruneisen parameters, and sample orientation. Phys. Rev. B 79, 205433 (2009).
Ni, Y., Chalopin, Y. & Volz, S. Few layer graphene based superlattices as efficient thermal insulators. Appl. Phys. Lett. 103, 141905 (2013).
Tongay, S. et al. Tuning interlayer coupling in large-area heterostructures with CVD-grown MoS2 and WS2 monolayers. Nano Lett. 14, 3185–3190 (2014).
Acknowledgements
C.D.Z., J.T.L.T. and K.H. acknowledge financial support from the A*Star Pharos Programme (Grant No. 152 70 00015). Y.L. and C.-W.Q. acknowledge the financial support from A*STAR Pharos Programme (Grant No. 152 70 00014, with Project No. R-263-000-B91-305). C.-W.Q. acknowledges the partial support from National University of Singapore (Grant No. R-263-000-C05-112). Z.Y.O. and G.Z. acknowledge financial support from the Science and Engineering Research Council (152-70-00017). K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan and a Grant-in-Aid for Scientific Research on Innovative Areas “Science of Atomic Layers” from JSPS.
Author information
Authors and Affiliations
Contributions
K.H. and J.T.L.T. conceived the project. L.Y. performed the measurements with help from W.J. and Y.Z. O.Z.Y. and G.Z. performed the NEGF calculations. K.W. and T.T. provided the high quality h-BN samples. C.Q.W., C.D.Z., J.T.L.T. and K.H. guided the project. All authors contributed to the writing and discussion of the manuscript. All authors have given approval to the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Liu, Y., Ong, ZY., Wu, J. et al. Thermal Conductance of the 2D MoS2/h-BN and graphene/h-BN Interfaces. Sci Rep 7, 43886 (2017). https://doi.org/10.1038/srep43886
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep43886
This article is cited by
-
Band Gap Engineered MoS2 Nanosheets-Anchored ZIF-8 Composite Towards Degradation and Reduction of Crystal Violet and Picric Acid in Wastewater
Journal of Inorganic and Organometallic Polymers and Materials (2024)
-
Enhanced composite thermal conductivity by percolated networks of in-situ confined-grown carbon nanotubes
Nano Research (2023)
-
A Review on Investigation of Graphene Thermal Property: Recent Development in Measurement Techniques
Multiscale Science and Engineering (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 peak, and h-BN as a function of Joule heating power of MoS2: as the power increases, the temperature also increases, indicated as Raman red-shifts.
peak, and h-BN as a function of Joule heating power of MoS2: as the power increases, the temperature also increases, indicated as Raman red-shifts.
