Abstract
Whether there is a general allometry law across plant species with different sizes and under different environment has long been controversial and shrubs are particularly useful to examine these questions. Here we sampled 939 individuals from 50 forest shrub species along a large altitudinal gradient. We tested several allometry models with four relationships simultaneously (between stem diameter, height, leaf, stem and aboveground biomass), including geometric, elastic and stress similarity, and metabolic scaling theory’s predictions on small plants (MSTs) and trees (MSTt). We also tested if allometric exponents change markedly with climate and phylogeny. The predicted exponents of MSTt, elastic similarity and stress similarity (models for trees) were not supported by our data, while MSTs and geometric similarity gained more support, suggesting the finite size effect is more important for shrub allometries than being a woody plant. The influence of climate and phylogeny on allometric exponents were not significant or very weak, again suggesting strong biophysical constraints on shrub allometries. Our results reveal clear differences of shrub allometries from previous findings on trees (e.g. much weaker climatic and phylogenic control). Comparisons of herbs, shrubs and trees along a same climatic gradient are needed for better understanding of plant allometries.
Similar content being viewed by others
Introduction
Whether there is a general allometry law across plant species with different sizes and under different environment has long been a focus in ecology1,2,3,4,5,6, and a number of hypotheses have been proposed to explore the underlying mechanisms. One group of hypotheses are based on assumptions of basic biophysical constraints on plant allometries and have provided testable predictions on scaling exponents (Table 1), including physical models (geometric7, elastic and stress similarity8,9) and biophysical ones (metabolic scaling theory, MST)5,10,11. The physical models consider some physical and geometric constraints of plants, such as isometrical scaling of organ length and radius (geometric similarity7), margin of safety of branches against mechanical failure (elastic similarity8,9) or the stress produced by wind pressure along the stem (stress similarity8,9). On the other hand, MST further considers biological constraints (e.g. maximization of metabolic rate) and predicts far more relationships than physical models. MST first proposed a model for tree allometries (MSTt, hereafter)5,11. However, subsequent MST studies demonstrated that the predictions for small plants (MSTs) should be different. This is because small plants (e.g. herbs) lack some key features of trees: high stature, branching networks with a large number of branchings12,13,14, and large amounts of secondary xylem15. For instance, for small plants MST predicted that (Table 1): H (height) ∝ D (Diameter), ML (leaf mass) ∝ MS (stem mass), MA (aboveground mass) ∝ D3 and MA ∝ H3 (for details, see Appendix 1).
These models are important in exploring the general allometric laws for plants5,11,16,17,18 and have attracted many research interests (especially MST). However, these models have also been controversial6,18,19,20,21,22. Thus further tests are still needed across species groups and regions, and some limitations in previous tests require attention. First, each model makes predictions for multiple allometric relationships (Table 1), which theoretically need to be tested simultaneously. However, many studies have tested only one or two predicted exponents of the models, which may lead to bias in rejecting the models18. Second, most tests have been conducted using data from trees5,9,20,23. Although some studies have tested MST with data including plants from herbs to large trees15,22,24,25, allometry data for shrubs are still rather limited compared with trees26.
Shrubs are particularly useful to test these models and to examine the size-dependence of plant allometries. On one hand, shrubs differ from herbs in that they have well-developed secondary xylem; thus they may support MSTt. On the other hand, shrubs differ from trees in that they typically have lower numbers of branches because of low stature (the finite size effects12), so they may support MSTs. Some studies have suggested that the elastic and stress similarity models were suitable for trees while geometric similarity suitable for small plants (though there is still no consensus)8,27,28. Since the stature of shrubs is more similar to herbs than trees and MST suggests that the finite size effects are important for plant allometries12,29, we predicted that our shrub data will provide more supports to MSTs and the geometric similarity model, instead of MSTt, elastic similarity or stress similarity.
In contrast to biophysical models that predict a single exponent for each relationship (Table 1), another group of studies have related allometries to environmental gradients and suggested that allometric exponents change markedly with climate and site quality21,23,30,31. For instance, the allometric exponent between mean tree height and mean biomass per stem (commonly used to test MSTt16,17) was found to be significantly affected by climate and dominant species in northeast China32. The scaling exponent of individual tree diameter with height has also been found to vary remarkably along climate gradients2,23,30,31. Meanwhile, the extent to which phylogeny affects allometric exponents is also controversial. The supporters of MST showed that allometric exponents do not differ much across a wide range of phylogenetic affiliations from herbs to trees4,16,33,34,35. However, others have found that allometric exponents differ among phylogenetic groups, species, and even intra-specifically18,21,23,31. Thus, the influence of climate and phylogeny on plant allometries still needs further examination.
Few studies have examined allometries of forest shrubs in relation to large climatic gradients. In this study, we sampled shrubs along the altitudinal gradient of Mt. Changbai in northeast China to examine three questions as follows: (1) Does shrub allometry conform to MSTs and geometric similarity rather than MSTt, elastic similarity or stress similarity? We tested these models with four allometric relationships simultaneously: height vs. stem diameter, leaf vs. stem biomass, aboveground biomass vs. height and vs. diameter. (2) Are shrub allometric exponents strongly affected by climate gradients and phylogeny (as observed by previous studies on trees), or only slightly affected as predicted by MST? If the latter is true, this may suggest biophysical constraints plays an important role in shaping the allometries of forest shrubs.
Results
Testing the biophysical models
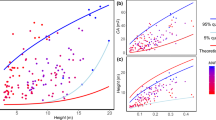
To test the models, we used data from all plots together (Fig. 1) and standard major axis (SMA) regression to examine whether the model predicted exponents were within the 95% confidence intervals (CIs) of SMA slope, for both raw data and phylogenetic independent contrasts (PIC) data (see Methods).
The five biophysical models differed markedly in their consistency with the observed data (Table 1). As predicted, the MSTt, elastic similarity and stress similarity models were not supported. For stress similarity, only one prediction (MA-D) was consistent with our raw data.
All four predictions of MSTs, and all the three predictions of geometric similarity, were supported in the PIC data. Some predictions of the two models were not consistent with the test using original data. Since the PIC test is more robust compared with the test with original data (see Methods), we concluded that our data provided more support to MSTs and geometric similarity than the other three models.
Influence of climate and phylogeny on allometric exponents
Three of the SMA slopes of the original and PIC data were not significantly different (Table 1). This suggests that phylogeny has no influence on most allometric exponents. Further, when the allometric exponents and intercepts of the 25 plots were related to mean annual temperature (MAT) and precipitation (MAP) along the altitudinal gradient (Table 2), only two of the 16 correlations were significant, suggesting that shrub allometries are also only weakly affected by climate.
These results were confirmed by a more detailed analysis with mixed-model analysis of variance (ANOVA) (Table 3). For allometric exponents (i.e. the interaction terms), climate had little influence. Only MAP had a significant relationship with the MA-D allometry, and MAT had a significant relationship with MA-H, but both explained negligible proportions of variance (0.12% and 0.39%, respectively). The effect of site (i.e. potential effect of other local conditions) was significant for all four allometric exponents, but still explained only 0.52% to 1.70% of variance. For the H-D and ML-MS relationships, none of the phylogenetic terms were significant (at P < 0.05). For MA-H and MA-D, only one term (e.g. the “log H: species” term) was significant, but again explained only 0.53% to 0.61% of variance. When the phylogenetic terms were replaced with taxonomic groups, the results were similar (Appendix 2). In summary, the effects of both climate and phylogeny on allometric exponents were very weak (if there were any) for the forest shrubs in this study.
For allometric constants (i.e. the effect of environmental and phylogenetic variables themselves), more variables were significant and explained more variation compared with the interaction terms (Table 3). This suggest that climate and phylogeny have some influence on shrub allometries, but mainly through allometric constants rather than exponents, which is consistent with a prediction of MST18,33,35. However, since most of the correlations of intercepts with climate were not significant (Table 2), this issue requires examination in future studies. Consequently, we will not comment on it further.
Discussion
Since the biophysical allometry models (Table 1) were proposed, much effort have been devoted to test them18,27,36. Each model has gained some level of support but has also been controversial.
Here we tested the models using a large shrub dataset along a large altitudinal gradient. Similar as MSTt, the elastic and stress similarity models were originally developed for tree allometries8, and were then extended to other plants and even animals. As we expected, they were not supported by our shrub forest data (Table 1). Though stress similarity have one prediction (MA-D) supported by the raw data, but other predictions could not be supported simultaneously. This implies that studies that use only one or two allometric relationships to test these biophysical models could well have reached stronger conclusions than warranted.
Metabolic scaling theory now days can account for different models of scaling (geometric, elastic similarity etc.) and suggests that allometric exponents change continuously with plant size rather than being constant as misunderstood in the literature12,37,38. MST suggests that plant vascular networks are self-similar and has derived that: lk ∝ rkα (where lk and rk is the length and radius of branches at the kth level in the branching network). When α = 2/3 (i.e. elastic similarity) for all k (i.e. self-similar), then the predictions for trees (MSTt) can be derived. For small plants, however, α = 1 (i.e. geometric similarity) for all k, which leads to the predictions of MSTs (for details see ref. 29). Price et al. (2007) further proposed a new version of MST38. By relaxing some assumptions of MSTt and explicitly addressing variation in network design, they showed that allometric exponents should change continuously with plant size, and the predictions of geometric similarity, elastic and stress similarity and the fractal branching model (i.e. MSTt) all fall along this continuum from the smallest herbs to the tallest trees. Shrubs are expected to be located near the end for small plants along this continuum because of finite size effects (see Introduction). This prediction was confirmed by our data, which provided more support to MSTs and geometric similarity compared with the other three models. Meanwhile, other MSTs predictions have also received supported from previous studies on small plants15,26. It seems that MST provides a basis to develop a general theory of plant allometry in the future.
While numerous allometric studies have been conducted, most were local-scale. Relative few papers have examined whether and how the scaling relationships of trees vary along climatic gradients23, and such studies are even rarer for shrubs. Despite this, existing evidence for trees indicates that allometric exponents change significantly with climate. This is true for other allometries as well as H-D scaling, and has been found in studies from regional to continental scales2,23,30,31,32,39,40.
Even so, in this analysis on shrubs we found that the exponents of four scaling relationships were largely unaffected by climate (Tables 2 and 3). We covered a large climate gradient from timberline to low-elevation temperate forests, which was comparable to that of Wang et al.30 in terms of temperature; but they found strong climatic control of tree H-D allometry in northeast China. Thus, our results suggest that there are real differences between shrubs and trees in the modulators of allometries.
For the tree growth form, the tall stature lead to great difficulty in water transportation from root to canopy (i.e. hydraulic resistance)41,42. While tapering of conduits from stem base to top is found to be an effective compensation mechanism43, it may only partially compensate for the increase in hydraulic resistance with tree height44. Many studies have found that the hydraulic efficiency of tree xylem is reduced in drier or colder climates45,46. Thus, trees have to adjust the relative biomass allocated for stem diameter, height and branch growth in response to climate gradient23,30. However, the situation is much different for shrubs. First, the low stature of shrub means that it has much lower hydraulic resistance than trees. Second, studies on tree and shrub physiology showed that conduit tapering can compensate for most hydraulic resistance for low stature plants but not for tall trees44,47,48. Thus, for forest shrubs under humid climate (e.g. in our study) there seems not much difficulty in vertical water transportation. This may be an important reason why the allometric exponents in our study were found to be insensitive to climate. However, our findings may not be easily extended to arid shrub or desert biomes, where very low soil water potential may still cause vertical water transportation to be difficult for shrubs.
Our results indicate that the effect of phylogeny on shrub allometries seem to be also very weak (Tables 1 and 3). This is again in contrast to studies on trees that revealed clear allometric differences among phylogenetic groups18,21,23,31,49. Why shrubs and trees may differ is still not clear and deserves further study. However, it seems that shrubs provide more support than trees to a prediction of metabolic scaling theory that allometric exponents were not sensitive to either environment or phylogeny3,16,33. Similarly, a recent study on understory shrubs in subtropical forests of China found that the scaling exponent of above- vs. below-ground biomass was consistent with MST for small plants, and was also insensitive to environmental variation and difference in species composition26. These results suggest that there are strong biophysical constraints on shrub allometries. Climate and phylogeny may play a secondary role in addition to biophysical constraints, and thus their effects on allometric exponents may be only obvious for trees.
Our result that the allometric exponents of forest shrubs are largely un-affected by climate gradient and phylogeny is important. Empirically, it helps to define numerically the boundary conditions for biomass allocation patterns across diverse shrub species and climate conditions50, and thus may contribute to a better estimation of forest understory carbon pools. The finding is also theoretically important because, it suggests that basic biophysical constraints are crucial in shaping shrub allometries, and that the modulators for small plant allometry differ markedly from that of trees. These differences between shrubs and trees may arise partly because of the difficulty in vertical water transportation for trees; and may also because hasher climate limits tree height30,42 which in turn leads to size-related changes in allometries37,38. Further, for trees the change of allometric exponents across climate gradients can be partially caused by environmentally driven recruitment limitation and successional status39. Which of these mechanisms is more important for plant allometries remains unclear. Thus, systematic comparisons of herb, shrub and tree allometries across the same climatic gradient are needed to address these questions.
Methods
The study area
Mt. Changbai (41°43′–42°26′N, 127°42′–128°17′E) is located at the border between Northeast China and North Korea. It is the highest mountain (2691 m) in Northeast Asia and all latitudinal forest zones in northeast China can be found along its altitudinal gradient. Thus, Mt. Changbai provides an ideal location to test ecological hypotheses related to climatic gradients51,52.
The regional climate is controlled by the East Asian monsoon, with warm summers, cold winters, abundant precipitation and a short growing season. With increasing altitude from the base to the top of Mt. Changbai, mean annual temperature decreases from 4.9 to −7.3 °C, and mean annual precipitation increases from 600 to 1340 mm53. As a result of the climatic gradients, three forest zones are distributed along the altitudinal gradient: (1) <1100 m: mixed broad- & needle-leaved forest, composed of Pinus koraiensis and broad-leaf species; (2) 1100–1700 m: evergreen needle-leaved forest, composed of Picea jezoensis and Abies nephrolepis; (3) 1700–2000 m: Betula ermanii forest54.
Sampling method and climate data
We set 25 plots of 20 m × 30 m along the altitudinal gradient, ranging from 450 m to 1900 m a.s.l., covering all the vertical forest zones of Mt. Changbai. We selected ca. 10 individuals of variable sizes of each dominant shrub species in the understory of each plot. We made efforts to avoid multi-stem individuals, and sampled only individuals with distinct main stem at the base (i.e. individuals that the base diameter can be measured). In a few cases, when this is not possible, we measured each stem separately for a multi-stem individuals, and other variables were also measured separately. We measured basal stem diameter and vertical height before harvesting the individuals. The dried weights of leaf and stem for each individual were determined by oven-drying for 72 h at 60 °C. A total of 939 individuals belonging to 50 shrub species (from 31 genera and 18 families) were sampled. Statistic descriptions of these variables are listed in Table 4.
The climatic data of the plots were estimated using the models developed by Wang et al.55. The models were fitted with data from climate stations across the Changbai Mountains and adjacent regions, in which monthly mean temperature and precipitation were estimated with linear models using latitude, longitude and altitude as predictors. Wang et al.55 validated their models using independent climate data, and have shown that the estimated climates were sufficiently accurate55. We initially calculated six climate variables for each plot, including mean annual temperature and precipitation (MAT and MAP, respectively), mean temperature of the coldest month, warmth index and coldness index, and annual range of temperature. A preliminary PCA analysis indicated that MAT and MAP represent the two major axes of climatic variation, and other climate variables were highly correlated with them. To avoid collinearities among predictors, we used only MAT and MAP in statistical analyses.
Phylogenetic tree and phylogenetic analyses
We constructed a phylogenetic tree for the 50 shrub species in this study to examine the effect of phylogeny on shrub allometries. The tree topology was built with the online program Phylomatic 256, using the “Maximally resolved seed plant tree (version R20091110)” based on the supertree of the Angiosperm Phylogeny Group III (APG III 2009). In many cases, the Phylomatic program treated genera as polytomies within their families while species as polytomies within their genera. We searched for phylogenies in literatures57,58,59 and online databases (www.timetree.org), and the polytomies were substituted with published phylogenies whenever available. The branch lengths of the phylogenetic tree were determined using the BLADJ program56, with the nodes ages available in Wikström et al.60 and other sources57,58,59 including www. timetree.org.
We used the phylogenetic tree (Fig. 2) for two analyses: (1) phylogenetic independent contrasts (PIC)61,62. Closely related species tend to have similar traits, thus there may be non-independence of data due to phylogeny when analyzing the relationship between traits across species. To test the predicted allometric exponents of the biophysical allometry models more robustly, we created PIC for each allometric variable (H, D, ML, MS and MA) using the Phylocom program56. We re-analyzed the allometric relationships using PIC (i.e. data when phylogenetic signals have been removed), in addition to the allometric analyses using original data.
(2) While the PIC approach is effective in removing phylogenetic signal, the method is not effective for examining how allometric relationships were affected by phylogeny and environmental factors together. For this purpose we created phylogenetic groups using the method described in He et al.63, by “cutting” the phylogenetic tree at 80 and 45 Mya (Fig. 1). We chose 80 and 45 Mya because they resulted in the same number of divisions (18 and 31, respectively) as the family or generic numbers of our species63. The phylogenetic groups thus created were then used as categorical variables in multivariate models of allometric relationships. This method has a great advantage that the relative effects of phylogenetic and environmental factors could be quantified and compared63,64. In this analysis, the non-independence of data (caused by phylogeny and site) was dealt with using mixed-model ANOVA, which will be described below.
Statistic analyses
We examined four allometric relationships simultaneously for a better test of the biophysical allometry models: height (H) vs. diameter (D), leaf (ML) vs. stem biomass (MS), aboveground biomass (MA) vs. height, and MA vs. D. All five variables were log-transformed prior to analysis. Allometric exponents and constants and their 95% confidence intervals (CIs) were obtained through linear regression of log-X and log-Y, a standard method in allometric analysis17. We used standard major axis (SMA) regression instead of ordinary least squares regression, because the latter can underestimate regression slope when both X and Y are measured with error. SMA analyses were conducted with the R package SMATR.
To test the biophysical models we used data from all plots to fit the four allometric relationships. For each relationship we examined whether the 95% CIs of the SMA slope included the predicted values of the biophysical models, using both the original and PIC data. To test the effect of phylogeny on allometries, we examined whether the SMA slopes of PIC were significantly different from that of original data, using the likelihood ratio test. If true, this indicates that phylogenetic relatedness significantly influences an allometric exponent.
We also fitted allometric relationships for each plot and correlated the plot-level SMA slopes and elevations with the climate indices of the plots to examine whether allometric relationships changed with climate. However, for a more detailed examination of the potential influence of environment and phylogeny on shrub allometries, we used general linear models (GLMs) and mixed-model ANOVA. For each allometric relationship, we explained log-Y using log-X together with other explanatory terms as follows: (1) climate (MAT and MAP); (2) site (i.e. the plots) was used as a categorical variable to account for other sources of environmental variation (e.g. canopy openness, soil fertility, etc.)65,66; (3) phylogenetic or taxonomic groups. Phylogenetic groups included three nested terms mentioned above: the 80 Mya and 45 Mya phylogenetic groups, and species. Taxonomic groups included family, genus and species. (4) The interactions between log-X and climate, site, and phylogenetic terms were included in GLMs to examine whether the regression slopes (i.e. allometric exponents) were significantly affected by environment and phylogenetic/taxonomic relationships.
In these analyses, climatic variables were nested within sites, and thus lead to non-independence of data. This problem was resolved by treating MAT and MAP as fixed factors while site as random effect in mixed-model ANOVA. The phylogenetic or taxonomic terms were also nested (e.g. genera nested within families). Thus, for the 80 Mya phylogenetic group (or family) the 45 Mya group (or genus) was used as the random effect; whereas for the 45 Mya group (or genus) the species term was treated as the random effect. Similarly, the interaction terms of climate and phylogeny with log-X were treated in a similar way (for details, see ref. 65). All statistical analyses were performed with R 3.3.167.
Additional Information
How to cite this article: Sun, H. et al. Effects of biophysical constraints, climate and phylogeny on forest shrub allometries along an altitudinal gradient in Northeast China. Sci. Rep. 7, 43769; doi: 10.1038/srep43769 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Chave, J. et al. Tree Allometry and Improved Estimation of Carbon Stocks and Balance in Tropical Forests. Oecologia. 145, 87–99 (2005).
Chave, J. et al. Improved Allometric Models to Estimate the Aboveground Biomass of Tropical Trees. Global Change Biol. 20, 3177–3190 (2014).
Enquist, B. J. & Niklas, K. J. Invariant Scaling Relations Across Tree-Dominated Communities. Nature. 410, 655–660 (2001).
Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M. & West, G. B. Toward a Metabolic Theory of Ecology. Ecology. 85, 1771–1789 (2004).
West, G. B., Brown, J. H. & Enquist, B. J. The Fourth Dimension of Life: Fractal Geometry and Allometric Scaling of Organisms. Science. 284, 1677–1679 (1999).
Apol, M. E. F., Etienne, R. S. & Han, O. Revisiting the Evolutionary Origin of Allometric Metabolic Scaling in Biology. Funct Ecol. 22, 1070–1080 (2008).
Rich, P. M. & Short, L. Height and Stem Diameter Relationships for Dicotyledonous Trees and Arborescent Palms of Costa Rican Tropical Wet Forest1. Bulletin of the Torrey Botanical Club. 113, 241–246 (1986).
Mcmahon, T. A. & Kronauer, R. E. Tree Structures: Deducing the Principle of Mechanical Design. J Theor Biol. 59, 443–466 (1976).
O’Brien, S. T., Hubbell, S. P., Spiro, P., Condit, R. & Foster, R. B. Diameter, Height, Crown, and Age Relationship in Eight Neotropical Tree Species. Ecology. 76, 1926–1939 (1995).
West, G. B., Brown, J. H. & Enquist, B. J. A General Model for the Origin of Allometric Scaling Laws in Biology. Science. 276, 122–126 (1997).
West, G. B., Brown, J. H. & Enquist, B. J. A General Model for the Structure and Allometry of Plant Vascular Systems. Nature. 400, 664–667 (1999).
Enquist, B. J. et al. Does the Exception Prove the Rule? Nature. 445, E9–E10, E10–E11 (2007).
Savage, V. M., Deeds, E. J. & Fontana, W. Sizing Up Allometric Scaling Theory. Plos Comput Biol. 4, e1000171 (2008).
Bentley, L. P. et al. An Empirical Assessment of Tree Branching Networks and Implications for Plant Allometric Scaling Models. Ecol Lett. 16, 1069–1078 (2013).
Niklas, K. J. A Phyletic Perspective On the Allometry of Plant Biomass-Partitioning Patterns and Functionally Equivalent Organ-Categories. New Phytol. 171, 27–40 (2006).
Niklas, K. J. & Enquist, B. J. Invariant Scaling Relationships for Interspecific Plant Biomass Production Rates and Body Size. Proc Natl Acad Sci USA 98, 2922–2927 (2001).
Enquist, B. J. & Niklas, K. J. Global Allocation Rules for Patterns of Biomass Partitioning in Seed Plants. Science. 295, 1517–1520 (2002).
Price, C. A., Ogle, K., White, E. P. & Weitz, J. S. Evaluating Scaling Models in Biology Using Hierarchical Bayesian Approaches. Ecol Lett. 12, 641–651 (2009).
Da, C. Challenges to the Generality of WBE Theory. Trends Ecol Evol. 21, 593–596 (2006).
Muller-Landau, H. C. et al. Testing Metabolic Ecology Theory for Allometric Scaling of Tree Size, Growth and Mortality in Tropical Forests. Ecol Lett. 9, 575–588 (2006).
White, C. R., Cassey, P. & Blackburn, T. M. Allometric Exponents Do Not Support a Universal Metabolic Allometry. Ecology. 88, 315–323 (2007).
Poorter, H. et al. How Does Biomass Distribution Change with Size and Differ Among Species? An Analysis for 1200 Plant Species From Five Continents. New Phytol. 208, 736–749 (2015).
Lines, E. R., Zavala, M. A., Purves, D. W. & Coomes, D. A. Predictable Changes in Aboveground Allometry of Trees Along Gradients of Temperature, Aridity and Competition. Global Ecol Biogeogr. 21, 1017–1028 (2012).
Enquist, B. J., Haskell, J. P. & Tiffney, B. H. General Patterns of Taxonomic and Biomass Partitioning in Extant and Fossil Plant Communities. Nature. 419, 610–613 (2002).
Price, C. A. & Enquist, B. J. Scaling of Mass and Morphology in Plants with Minimal Branching: An Extension of the WBE Model. Funct Ecol. 20, 11–20 (2006).
Cheng, D. et al. Isometric Scaling of Above- and Below-Ground Biomass at the Individual and Community Levels in the Understorey of a Sub-Tropical Forest. Ann Bot-London. 115, 303–313 (2015).
Norberg, R. A. Theory of Growth Geometry of Plants and Self-Thinning of Plant Populations: Geometric Similarity, Elastic Similarity, and Different Growth Modes of Plant Parts. Am Nat. 131, 220–256 (1988).
Biewener, A. A. Biomechanical Consequences of Scaling. J Exp Biol. 208, 1665–1676 (2005).
Enquist, B. J. Universal Scaling in Tree and Vascular Plant Allometry: Toward a General Quantitative Theory Linking Plant Form and Function From Cells to Ecosystems. Tree Physiol. 22, 1045–1064 (2002).
Wang, X., Fang, J., Tang, Z. & Zhu, B. Climatic Control of Primary Forest Structure and DBH-height Allometry in Northeast China. Forest Ecology & Management. 234, 264–274 (2006).
Hulshof, C. M., Swenson, N. G. & Weiser, M. D. Tree Height–Diameter Allometry Across the United States. Ecology & Evolution. 5, 1193–1204 (2015).
Wang, X., Ouyang, S., Sun, O. J. & Fang, J. Forest Biomass Patterns Across Northeast China are Strongly Shaped by Forest Height. Forest Ecol Manag. 293, 149–160 (2013).
Niklas, K. J. & Enquist, B. J. Canonical Rules for Plant Organ Biomass Partitioning and Annual Allocation. Am J Bot. 89, 812–819 (2002).
Niklas, K. J. Plant Allometry: Is there a Grand Unifying Theory? Biol Rev. 79, 871–889 (1999).
Mccarthy, M. C. & Enquist, B. J. Consistency Between an Allometric Approach and Optimal Partitioning Theory in Global Patterns of Plant Biomass Allocation. Funct Ecol. 21, 713–720 (2007).
O’Brien, E. M. Climatic Gradients in Woody Plant Species Richness: Towards an Explanation Based on an Analysis of Southern Africa’s Woody Flora. J Biogeogr. 20, 181–198 (1993).
Niklas, K. J. & Spatz, H. C. Growth and Hydraulic (Not Mechanical) Constraints Govern the Scaling of Tree Height and Mass. P Natl Acad Sci USA 101, 15661–15663 (2004).
Price, C. A., Enquist, B. J. & Savage, V. M. A General Model for Allometric Covariation in Botanical Form and Function. P Natl Acad Sci USA 104, 13204–13209 (2007).
Duncanson, L. I., Dubayah, R. O. & Enquist, B. J. Assessing the General Patterns of Forest Structure: Quantifying Tree and Forest Allometric Scaling Relationships in the United States. Global Ecology & Biogeography. 24, 1465–1475 (2015).
Feldpausch, T. R. et al. Height-Diameter Allometry of Tropical Forest Trees. Biogeosciences. 8, 7727–7793 (2011).
Ryan, M. G. & Yoder, B. J. Hydraulic Limits to Tree Height and Tree Growth. Bioscience. 47, 235–242 (1997).
Ryan, M. G., Phillips, N. & Bond, B. J. The Hydraulic Limitation Hypothesis Revisited. Plant Cell & Environment. 29, 367–381 (2006).
Zimmermann, M. H. Hydraulic architecture of some diffuse-porous trees. Can J Bot. 56, 2286–2295 (1978).
Petit, G., Anfodillo, T. & Mencuccini, M. Tapering of Xylem Conduits and Hydraulic Limitations in Sycamore (Acer pseudoplatanus) Trees. New Phytol. 177, 653–664 (2008).
Ryan, M. G. & Yoder, B. J. Hydraulic Limits to Tree Height and Tree Growth. BioScience. 47, 235–242 (1997).
Petit, G., Anfodillo, T., Carraro, V., Grani, F. & Carrer, M. Hydraulic Constraints Limit Height Growth in Trees at High Altitude. New Phytol. 189, 241–252 (2011).
Petit, G. & Anfodillo, T. Plant Physiology in Theory and Practice: An Analysis of the WBE Model for Vascular Plants. J Theor Biol. 259, 1–4 (2009).
Issoufou, H. B. et al. Is the WBE Model Appropriate for Semi-arid Shrubs Subjected to Clear Cutting? Tree Physiol. 35, 197–208 (2015).
Ducey, M. J. Evergreenness and Wood Density Predict Height–Diameter Scaling in Trees of the Northeastern United States. Forest Ecology & Management. 279, 21–26 (2012).
Cheng, D. et al. Above- and Below-ground Biomass Relationships Across 1534 Forested Communities. Ann Bot-London. 99, 95–102 (2007).
Wang, X., Fang, J., Sanders, N. J., White, P. S. & Tang, Z. Relative Importance of Climate Vs Local Factors in Shaping the Regional Patterns of Forest Plant Richness Across Northeast China. Ecography. 32, 133–142 (2009).
Fang, J. et al. Multi-Scale Patterns of Forest Structure and Species Composition in Relation to Climate in Northeast China. Ecography. 35, 1072–1082 (2012).
Zhang, F., Chi, Z. & Li, X. The analysis and primary evaluation on the climate of Changbai mountain area. Research of Forest Ecosystem 1, 193–214 (1980).
Wang, Z. et al. The main forest types and their features of community structure in Northern slope of Changbai Mountain (I). Research of Forest Ecosystem 1, 25–42 (1980).
Wang, X., Fang, J. & Zhu, B. Forest Biomass and Root–Shoot Allocation in Northeast China. Forest Ecology & Management. 255, 4007–4020 (2008).
Webb, C. O., Ackerly, D. D. & Kembel, S. W. Phylocom: Software for the Analysis of Phylogenetic Community Structure and Trait Evolution. Bioinformatics. 24, 2098–2100 (2008).
Eriksson, T. & Hibbs, M. S. Phylogenetic Analysis of Potentilla Using DNA Sequences of Nuclear Ribosomal Internal Transcribed Spacers (its), and Implications for the Classification of Rosoideae (Rosaceae). Plant Systematics & Evolution. 211, 155–179 (1998).
Messinger, W., Hummer, K. & Liston, A. Ribes (Grossulariaceae) Phylogeny as Indicated by Restriction-Site Polymorphisms of PCR-amplified Chloroplast DNA. Plant Systematics & Evolution. 217, 185–195 (1999).
Potter, D. et al. Phylogeny and Classification of Rosaceae. Plant Systematics & Evolution. 266, 5–43 (2007).
Wikström, N., Savolainen, V. & Chase, M. W. Evolution of the Angiosperms: Calibrating the Family Tree. Proceedings of the Royal Society B Biological Sciences. 268, 2211–2220 (2001).
Felsenstein, J. Phylogenies and the Comparative Method. Am Nat. 125, 1–15 (1985).
Garland, T., Harvey, P. H. & Ives, A. R. Procedures for the Analysis of Comparative Data Using Phylogenetically Independent Contrasts. Syst Biol. 41, 18–32 (1992).
He, J. S. et al. Taxonomic, Phylogenetic, and Environmental Trade-Offs Between Leaf Productivity and Persistence. Ecology. 90, 2779–2791 (2009).
Liu, C. et al. Relative Effects of Phylogeny, Biological Characters and Environments On Leaf Traits in Shrub Biomes Across Central Inner Mongolia, China. J Plant Ecol. 6, 220–231 (2013).
Balvanera, P. et al. Quantifying the Evidence for Biodiversity Effects On Ecosystem Functioning and Services. Ecol Lett. 9, 1146–1156 (2006).
Wu, X. et al. The Relationship Between Species Richness and Biomass Changes From Boreal to Subtropical Forests in China. Ecography. 38, 602–613 (2014).
R. Core Team R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL http://www.R-project.org/ (2013).
Acknowledgements
This study was supported by the National Natural Science Foundation of China (31370620). We specially thank L. B. Zeng, N. Zhao, S. Y. Ye, S. Dai, Z. J. Zhang, H.C. Zhou, Y. Sun and Z. J. Zong for participation or help in the field. We would also thank B. A. Hawkins and two referees for insightful and constructive comments.
Author information
Authors and Affiliations
Contributions
X.W. and W.Y. planed the study, H.S., Y.F., C.L., P.W., Q.L. collected the data, H.S. did the statistical analyses, H.S. and X.W. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sun, H., Wang, X., Fan, Y. et al. Effects of biophysical constraints, climate and phylogeny on forest shrub allometries along an altitudinal gradient in Northeast China. Sci Rep 7, 43769 (2017). https://doi.org/10.1038/srep43769
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep43769
This article is cited by
-
Allometric relationships between stem diameter, height and crown area of associated trees of cocoa agroforests of Ghana
Scientific Reports (2023)
-
Effects of climate, biotic factors, and phylogeny on allometric relationships: testing the metabolic scaling theory in plantations and natural forests across China
Forest Ecosystems (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.