Abstract
Graphene plasmonics has become a highlighted research area due to the outstanding properties of deep-subwavelength plasmon excitation, long relaxation time, and electro-optical tunability. Although the giant conductivity of a graphene layer enables the low-dimensional confinement of light, the atomic scale of the layer thickness is severely mismatched with optical mode sizes, which impedes the efficient tuning of graphene plasmon modes from the degraded light-graphene overlap. Inspired by gap plasmon modes in noble metals, here we propose low-dimensional hybrid graphene gap plasmon waves for large light-graphene overlap factor. We show that gap plasmon waves exhibit improved in-plane and out-of-plane field concentrations on graphene compared to those of edge or wire-like graphene plasmons. By adjusting the chemical property of the graphene layer, efficient and linear modulation of hybrid graphene gap plasmon modes is also achieved. Our results provide potential opportunities to low-dimensional graphene plasmonic devices with strong tunability.
Similar content being viewed by others
Introduction
In the context of light-matter interactions, the concentration of electromagnetic fields on materials is a critical issue for the performance of tunable optical devices, such as photodetectors1, bio-sensors2, optical modulators3,4, and lasers5. Plasmonic structures6,7,8,9 have thus been intensively studied to achieve subwavelength field concentration. For the design of plasmonic devices, the proper selection of metals determines the boundary of device performances10 for power consumption, bandwidth, and footprints.
Due to its two-dimensional (2D) structure with extremely large conductivity from the massless Dirac point11,12, graphene has become a leading candidate for deep-subwavelength plasmonics13,14,15. Along with its structural advantage for the integration, the giant and tunable conductivity of the graphene layer also enables the modulation of its optical properties. A number of devices such as absorbers16,17,18, modulators19,20, and tunable metamaterials21,22,23,24,25 controlling optical flows through the designed graphene layer have been proposed and demonstrated, by manipulating the dispersion of graphene conductivity via electric gating21,26,27,28 or chemical doping29,30. However, the atomically-thin graphene layer leads to the intrinsic limit for the device performance at the same time; while the mismatch between the wavelength of light and graphene layers hinders the excitation to graphene-based devices, the significant scale mismatch between ~10 nm to ~100 nm size optical modes and ~Å-scale graphene layers severely degrades the light-graphene overlap which prohibits the efficient manipulation of light flows in terms of light-matter interactions. The achievement of small modal size31,32 and more importantly, the high overlap factor with the graphene layer, is thus an urgent issue for tunable graphene plasmonics.
Here, we focus on low-dimensional waveguide systems for the improved light-graphene overlap factor. We firstly reveal the existence of hybrid graphene gap plasmon (H-GGP) modes the field profile of which is strongly confined inside the graphene gap between metallic and dielectric graphene layers. We demonstrate that the H-GGP mode has larger field concentration on graphene layers than those of edge33,34 or wire-like graphene plasmon modes31. By exploiting the tunable graphene conductivity through the chemical potential modulation, highly sensitive and linear modulation of the H-GGP propagation constant is also achieved with its stable mode profile. The proposed low-dimensional waveguide systems with the improved overlap factor pave the path toward integrated plasmonic devices on graphene.
Results
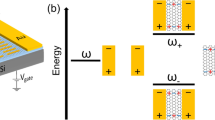
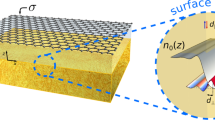
We consider the 2D metal-gap-dielectric waveguide system composed of three distinct graphene domains (Fig. 1a); a dielectric gap domain G with the width w (the sheet conductivity σ(G) where Im{σ(G)} < 0) is inserted in-between semi-infinite metallic domain M (Im{σ(M)} > 0) and dielectric domain D (Im{σ(D)} < 0). The gap region G satisfies the condition of Im{σ(D)} < Im{σ(G)} < 0, as the analogy of plasmonic gap modes in noble metals8,9. Note that such a system can be achieved by applying the spatial variation of the conductivity on a single graphene layer, based on the tuning of its chemical potential21,26,27,28 (or doping level) μ(x). Figure 1b shows the μ-dependency of the graphene conductivity calculated by Kubo formula11,21,23, which determines the operation regime for each layer (frequency f = ω/2π = 20 THz, charged particle scattering rate11 Γ = 0.43 meV, and temperature T = 3 K). To satisfy the gap mode condition as similar to the case of noble metals8,9, the proposed system can be realized by adjusting the doping level of each graphene region corresponding to (Ω(M))−1 > 0.6 and 0.5 < (Ω(D))−1 < (Ω(G))−1 < 0.6, where Ω−1 = μ/(ℏω) is the normalized chemical potential.
(a) A schematic of the proposed 2D metal-gap-dielectric system, composed of a gap domain G (dielectric, 0 < x < w; σ(G)) between two semi-infinite domains M (metallic, x < 0; σ(M)) and D (dielectric, x > w; σ(D)). The H-GGP mode is assumed to propagate along the y-axis with the wavevector q = q k . (b) The graphene conductivity as a function of the normalized chemical potential Ω−1, satisfying the condition of Im{σ(D)} < Im{σ(G)} < 0 < Im{σ(M)}. The blue-green (or yellow) region denotes the dielectric (or metallic) regime with 0.5 < Ω−1 < 0.6 (or Ω−1 > 0.6). The highly-lossy region (Ω−1 < 0.5 with Re(σ) > > 0) from the interband transition is excluded in our discussion. Graphene structures considered here are assumed to be suspended in air.
Figure 2a shows the electric field profile of the low-dimensional H-GGP mode in the 2D metal-gap-dielectric waveguide system, calculated by the eigenmode solver of COMSOL Multiphysics (w = 5 nm, (Ω(M))−1 = 4, (Ω(G))−1 = 0.54, and (Ω(D))−1 = 0.5002). In the numerical analysis, the graphene is considered as the film21 with the thickness31 of δ = 0.2 nm and the relative bulk permittivity of εg(ω) = 1 + jσg(ω)/(ωε0δ), where σg is sheet conductivity of graphene obtained from Kubo formula11 (Fig. 1b). To demonstrate the distinctive feature of H-GGP modes, we compare with other graphene waveguide modes: graphene edge plasmon (GEP) mode33,34 (Fig. 2b) and wire-like 1D-SPP mode31 (Fig. 2c) with same material parameters. While both H-GGP and 1D-SPP modes with quasi-antisymmetric potential profiles (σ(x, z)~ − σ(−x, z) for all z) have improved confinement compared to that of the GEP mode with much stronger structural asymmetry (|σ(x,0)| ≪ |σ(−x,0)| and |σ(x, z)| = |σ(−x, z)| for z ≠ 0), H-GGP exhibits more confined transverse (Ex) field on the gap region than that of the 1D-SPP mode, as similar to the difference between gap plasmons and surface plasmons in noble metals8,9. This transverse concentration originates from the continuity condition of the displacement current Im{σ(G)}·Ex(G)~Im{σ(D)}·Ex(D), deriving the enhancement of Ex(G) from the condition of Im{σ(D)} < Im{σ(G)} < 0. For the practical realization, we also note that H-GGP modes can be obtained at any finite temperatures when the conductivity of each domain satisfies the condition of Im{σ(D)} < Im{σ(G)} < 0 < Im{σ(M)}, as shown in Supplementary Note 1, demonstrating the existence of H-GGP modes in room temperature (T = 300 K), at the frequency of f = 100 THz.
Electric field distributions of graphene plasmon modes for (a) H-GGP mode (w = 5 nm and (Ω(G))−1 = 0.54), (b) GEP mode, and (c) wire-like 1D-SPP mode. (Ω(M))−1 = 4 for all cases, and (Ω(D))−1 = 0.5002 for (a,c). The horizontal black lines indicate graphene layers. The components of electric fields Ex,z are normalized for clarity.
Figure 3 shows the characteristics of the H-GGP mode, including effective mode index, intensity profiles, and field concentration. As similar to the case of noble metal gap plasmons35, many aspects of the H-GGP mode represent the intermediate features between those of 1D-SPP modes for low and high dielectric graphene layers. For example, the proposed H-GGP system with zero width (w = 0) corresponds to the σ(M) − σ(D) 1D-SPP system with the effective mode index31 of neff = Re{q}/k0 ≈ 2·(3/2)1/2·εε0·c/(Im{σ(M)} + Im{σ(D)}), while the H-GGP system with infinite w is converged to the σ(M) − σ(G) 1D-SPP system. The effective mode index (Fig. 3a) and the modal size (Fig. 3b) of the H-GGP mode with different widths are thus varying between these two boundaries.
(a) Effective mode index neff = Re{q}/k0 of the H-GGP mode as a function of the gap width w. (b) Modal cross section contours corresponding to w = 1, 10, 20, and 30 nm, which depict the region A for ∫∫A| E |2·d S /∫∫| E |2·d S = 0.8. (c) Electric field intensity along the center of the graphene layer (x-axis) for different gap widths w, compared to the cases of σ(M) − σ(D) and σ(M) − σ(G) 1D-SPP systems. (d) Graphene field concentration ρ as a function of the gap width w (wmax = 5 nm, wcut-off = 40 nm). The blue dashed (green dashed) line in (a–d) denotes 1D-SPP modes. All other parameters are same as those in Fig. 2.
Most importantly, there exist differentiated features of the H-GGP mode when compared to 1D-SPP modes, as shown in Fig. 3c and d. Figure 3c shows the electric field intensity of the H-GGP modes along the center of the graphene layer for different gap width (2 nm to 30 nm). Although the intensity profile of large w case is converged to that of the σ(M) − σ(G) 1D-SPP system, smaller w cases exhibit the intensity profiles focused of the graphene gap. Such a distinct in-plane intensity distribution imposes the unique property on out-of-plane confinement, in terms of the light-graphene overlap factor ρ = ∫∫graphene| E |2·d S /∫∫| E |2·d S : the concentration of electromagnetic fields on graphene. Figure 3d presents the variation of ρ as a function of the gap width w, which demonstrates the improved light-graphene overlap for the structures with apparent field concentration on the gap (0 < w < 40 nm). We note that the H-GGP mode acquires much higher field concentration on the graphene layer (ρ = 2.07 × 10−3 at w = 5 nm), when compared to those of 1D-SPP modes (σ(M) − σ(D) system of ρ = 1.81 × 10−3 and σ(M) − σ(G) system of ρ = 1.70 × 10−3) and the GEP mode (ρ = 0.728 × 10−3).
The large overlap factor in Fig. 3 allows for the enhancement of light-graphene interactions. Figure 4 shows the modulation of H-GGP modes by controlling the chemical potential of the graphene layer as (Ω(M))−1 = 4 + ΔΩ−1, (Ω(G))−1 = 0.54 + ΔΩ−1, and (Ω(D))−1 = 0.5002 + ΔΩ−1, with the spatially global (Fig. 4a) and local (Fig. 4b, 3wmax modulation width) modulation range. As seen, the effective mode index of the H-GGP mode can be controlled with an order of smaller modulation of ΔΩ−1 when compared to the GEP mode. The H-GGP mode also provides more efficient regime of ΔΩ−1 for controlling effective index compared to 1D-SPP modes (ΔΩ−1 ≤ 0.015). Such improved efficiency is more apparent for the case of the finite modulation region for ΔΩ−1 (dotted lines in Fig. 4c, for the 3wmax modulation width around the graphene gap), due to the improved transverse localization of the H-GGP mode (Fig. 3c). Note that the spatial profile of electric field intensity (Fig. 4d) and the overlap factor ρ (Fig. 4e) of the H-GGP mode is highly stable to the change of ΔΩ−1. This stability allows the adiabatic change of the propagation feature of the H-GGP mode, which is the origin of the linear variation of neff versus ΔΩ−1 in Fig. 4c. Because the change of chemical potentials is usually derived by the external electric field, the sensitive and linear modulation of the H-GGP mode demonstrated in Fig. 4 enables the high-speed and low-power realization of tunable graphene devices.
The schematics of the chemical potential modulation for cases of spatially (a) global and (b) local (3wmax modulation width) modulations on the transverse plane. Yellow regions in (a,b) indicate the modulation range. (c) The variation of effective mode index neff for H-GGP, 1D-SPP, and GEP modes for the case of wmax = 5 nm, as a function of the chemical potential modulation ΔΩ−1. Dashed lines denote the case of the spatially local modulation on the transverse plane (Fig.4b). (d) Electric field intensity of the H-GGP mode along the center of the graphene layer (x-axis), for different values of ΔΩ−1. (e) Graphene field concentration factor ρ as a function of ΔΩ−1. GEP mode exhibits much lower ρ in (e) (ρ~0.728 × 10−3, not shown). All other parameters are same as those in Fig. 2. See Supplementary Fig. 2 for the schematics of the modulation range for the cases of 1D-SPP modes (solid and dotted lines of blue and green colors).
Discussion
We demonstrated the existence of low-dimensional gap plasmon modes on graphene, which supports large light-graphene overlap factor. The system with spatially-varying chemical potential (or doping level) for H-GGP modes can be realized by several existing schemes such as electric field bias21 or substrate level control36. Highly efficient manipulation with the stable field profile of the H-GGP mode, improved from those of GEP33,34 or wire-like 1D-SPP modes31, opens the pathway toward tunable graphene plasmonics with high-speed and low-power operation. The modal profile dependency of the light-graphene overlap factor also imposes intriguing opportunity on unconventional wave profiles supported by 2D materials, based on optical transformation techniques21,37,38. In terms of future applications, the compensation method of the large difference between effective mode index of graphene plasmonics and that of air (n = 1) will be required for increasing excitation efficiency, for example, by applying adiabatic procedure or matched layers.
Additional Information
How to cite this article: Kim, Y. et al. Low-dimensional gap plasmons for enhanced light-graphene interactions. Sci. Rep. 7, 43333; doi: 10.1038/srep43333 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Tang, L. et al. Nanometre-scale germanium photodetector enhanced by a near-infrared dipole antenna. Nat. Photon. 2, 226–229 (2008).
Yang, A. H. et al. Optical manipulation of nanoparticles and biomolecules in sub-wavelength slot waveguides. Nature 457, 71–75 (2009).
Nozaki, K. et al. Sub-femtojoule all-optical switching using a photonic-crystal nanocavity. Nat. Photon. 4, 477–483 (2010).
Piao, X., Yu, S. & Park, N. Control of Fano asymmetry in plasmon induced transparency and its application to plasmonic waveguide modulator. Opt. Express 20, 18994–18999 (2012).
Oulton, R. F. et al. Plasmon lasers at deep subwavelength scale. Nature 461, 629–632 (2009).
Schuller, J. A. et al. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 9, 193–204 (2010).
Luk’yanchuk, B. et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 9, 707–715 (2010).
Oulton, R. F., Sorger, V. J., Genov, D. A., Pile, D. F. P. & Zhang, X. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photon. 2, 496–500 (2008).
Bian, Y. et al. Hybrid wedge plasmon polariton waveguide with good fabrication-error-tolerance for ultra-deep-subwavelength mode confinement. Opt. Express 19, 22417–22422 (2011).
Tassin, P., Koschny, T., Kafesaki, M. & Soukoulis, C. M. A comparison of graphene, superconductors and metals as conductors for metamaterials and plasmonics. Nat. Photon. 6, 259–264 (2012).
Gusynin, V. P., Sharapov, S. G. & Carbotte, J. P. Magneto-optical conductivity in graphene. J. Phys.: Condens. Matter 19, 026222 (2007).
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).
Koppens, F. H., Chang, D. E. & Garcia de Abajo, F. J. Graphene plasmonics: a platform for strong light-matter interactions. Nano Lett. 11, 3370–3377 (2011).
Grigorenko, A. N., Polini, M. & Novoselov, K. S. Graphene plasmonics. Nat. Photon. 6, 749–758 (2012).
Bao, Q. & Loh, K. P. Graphene Photonics Plasmonics and Broadband Optoelectronic Devices. ACS Nano 6, 3677–3694 (2012).
Thongrattanasiri, S., Koppens, F. H. & Garcia de Abajo, F. J. Complete optical absorption in periodically patterned graphene. Phys. Rev. Lett. 108, 047401 (2012).
Fang, Z. et al. Active tunable absorption enhancement with graphene nanodisk arrays. Nano Lett. 14, 299–304 (2014).
Yao, Y. et al. Electrically tunable metasurface perfect absorbers for ultrathin mid-infrared optical modulators. Nano Lett. 14, 6526–6532 (2014).
Liu, M. et al. A graphene-based broadband optical modulator. Nature 474, 64–67 (2011).
Phare, C. T., Daniel Lee, Y.-H., Cardenas, J. & Lipson, M. Graphene electro-optic modulator with 30 GHz bandwidth. Nat. Photon. 9, 511–514 (2015).
Vakil, A. & Engheta, N. Transformation optics using graphene. Science 332, 1291–1294 (2011).
Ju, L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotech. 6, 630–634 (2011).
Fallahi, A. & Perruisseau-Carrier, J. Design of tunable biperiodic graphene metasurfaces. Phys. Rev. B 86, 195408 (2012).
Mousavi, S. H. et al. Inductive tuning of Fano-resonant metasurfaces using plasmonic response of graphene in the mid-infrared. Nano Lett. 13, 1111–1117 (2013).
Li, Z. et al. Graphene Plasmonic Metasurfaces to Steer Infrared Light. Sci. Rep. 5, 12423 (2015).
Chen, J. et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 487, 77–81 (2012).
Fang, Z. et al. Gated Tunability and Hybridization of Localized Plasmons in Nanostructured Graphene. ACS Nano 7, 2388–2395 (2013).
Brar, V. W., Jang, M. S., Sherrott, M., Lopez, J. J. & Atwater, H. A. Highly confined tunable mid-infrared plasmonics in graphene nanoresonators. Nano Lett. 13, 2541–2547 (2013).
Yan, H. et al. Infrared Spectroscopy of Wafer-Scale Graphene. ACS Nano 5, 9854–9860 (2011).
Yan, H. et al. Damping pathways of mid-infrared plasmons in graphene nanostructures. Nat. Photon. 7, 394–399 (2013).
Mason, D. R., Menabde, S. G., Yu, S. & Park, N. Plasmonic excitations of 1D metal-dielectric interfaces in 2D systems: 1D surface plasmon polaritons. Sci. Rep. 4, 4536 (2014).
De Angelis, C., Locatelli, A., Mutti, A. & Aceves, A. Coupling dynamics of 1D surface plasmon polaritons in hybrid graphene systems. Opt. Lett. 41, 480–483 (2016).
Nikitin, A. Y., Guinea, F., García-Vidal, F. J. & Martín-Moreno, L. Edge and waveguide terahertz surface plasmon modes in graphene microribbons. Phys. Rev. B 84, 161407 (2011).
Wang, W., Apell, P. & Kinaret, J. Edge plasmons in graphene nanostructures. Phys. Rev. B 84, 085423 (2011).
Karalis, A., Lidorikis, E., Ibanescu, M., Joannopoulos, J. D. & Soljacic, M. Surface-plasmon-assisted guiding of broadband slow and subwavelength light in air. Phys. Rev. Lett. 95, 063901 (2005).
Goncher, S. J., Zhao, L., Pasupathy, A. N. & Flynn, G. W. Substrate level control of the local doping in graphene. Nano Lett. 13, 1386–1392 (2013).
Yu, S., Piao, X., Hong, J. & Park, N. Bloch-like waves in random-walk potentials based on supersymmetry. Nat. Comm. 6, 8269 (2015).
Heinrich, M. et al. Supersymmetric mode converters. Nat. Comm. 5, 3698 (2014).
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) through the Global Frontier Program (GFP) NRF-2014M3A6B3063708 and the Global Research Laboratory (GRL) Program K20815000003, which are all funded by the Ministry of Science, ICT & Future Planning of the Korean government. S. Yu was also supported by the Basic Science Research Program (2016R1A6A3A04009723) through the NRF, funded by the Ministry of Education of the Korean government.
Author information
Authors and Affiliations
Contributions
Y.K. developed the theory and performed eigenmode computations. S.Y. conceived the presented idea for the H-GGP mode and its light-graphene overlap factor. N.P. encouraged Y.K. and S.Y. to investigate unconventional graphene plasmon modes while supervising the findings of this work. All authors discussed the results and contributed to the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kim, Y., Yu, S. & Park, N. Low-dimensional gap plasmons for enhanced light-graphene interactions. Sci Rep 7, 43333 (2017). https://doi.org/10.1038/srep43333
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep43333
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.